基于解析解和修正Newton-Raphson法的土層固結參數反分析研究

黃大中

(鐵道第三勘察設計院集團有限公司，天津　300251)

?

基于解析解和修正Newton-Raphson法的土層固結參數反分析研究

黃大中

(鐵道第三勘察設計院集團有限公司，天津300251)

土體固結參數的準確性是影響土層沉降變形計算精度的重要因素，常規室內試驗獲得的土體固結參數受擾動較大，精度無法滿足精確計算需求。基于土層固結解析解和修正Newton-Raphson方法，建立通過土層沉降變形監測值反分析土層固結參數的優化求解模型，實現了對土體固結參數(體積壓縮系數、滲透系數)和初始固結時間的準確估計，可滿足工程中準確預測土層沉降變形隨時間發展變化的需求。

解析解Newton-Raphson法固結參數反分析

巖土工程中計算上部堆載、地下水位下降引發的土層沉降變形需要利用土體的固結參數，包括體積壓縮系數mv和滲透系數k，土體固結參數值的準確性直接影響土層沉降變形計算的精度。目前，土體的固結參數主要通過室內壓縮和滲透試驗確定[1-2]，由于土樣在鉆取、運輸和試驗操作過程中易受擾動，因此室內試驗測定參數值與實際值往往存在較大的誤差，無法準確反映實際工程狀況[3-5]。

反分析是當前巖土工程研究的一個重點領域，提供了獲取巖土參數的一條新途徑[6-7]。針對土層固結問題，很多學者利用現場實測的沉降量對固結系數cv進行反演計算，包括圖解法、最小二乘法、Asaoka法、遺傳算法等[8-11]。固結系數是由體積壓縮系數和滲透系數計算得出的綜合性指標，只能反映土層固結發展趨勢，無法用于土層沉降值計算。另外，由于沉降監測的初次記錄時間與起始固結時間常常存在一定時間間隔，沉降監測記錄時間點相比真實的固結時間點存在一定的誤差。綜上所述，目前尚未有根據土層沉降變形監測值對土層體積壓縮系數、滲透系數和初始固結時間3個指標同時進行反分析的研究。

利用土層沉降變形監測值，建立能綜合反映各時間點下沉降監測權重的目標函數，結合土層固結解析解，利用修正Newton-Raphson方法對體積壓縮系數、滲透系數和初始固結時間進行優化反演。算例應用表明，建立的反演分析模型具有良好的收斂性，能夠得出符合實際的土體固結參數值，可以進一步用于預測以后的土層沉降發展狀況。

1　土層固結解析解

圖1　大面積荷載引發的土層固結示意

由大面積荷載引發的土層固結如圖1所示，土層上部受荷載p作用，上下表面透水，初始超靜孔隙水壓力均勻分布為p，土層厚度為H，體積壓縮系數為mv，滲透系數為k。

土層在荷載作用下固結問題的控制方程為

(1)

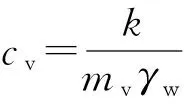
根據邊界條件可求得土層表面沉降變形的解析解[12]

(2)

式中，M=(2n-1)π，n=1，2，3，…。

由區域地下水位下降引發的土層固結如圖2所示，土層上部含水層(潛水層)水位恒定不變，初始時刻土層下部含水層(承壓層)水位下降量為hc，土體厚度為H，體積壓縮系數為mv，滲透系數為k。

圖2　水位下降引發的土層固結示意

土層由水位下降引發的固結問題控制方程與式(1)一致，根據邊界條件可求得土層表面沉降變形的解析解為[13]

(3)

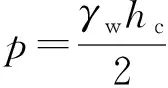
假定對土層沉降開始進行監測記錄時，土層已發生固結的時間為t0，則土層的沉降表達式為

(4)

式中，t為監測記錄時間。

2　固結參數反分析模型

根據沉降監測數據反演土體固結參數及初始固結時間時，需要設定合理的目標函數。為充分體現各個時間點下沉降值的權重，設定反分析的目標函數為

(5)

式中，s為按式(4)計算得出的沉降值；si為ti時刻土層的沉降量監測值；N為監測值記錄數。

對土層固結參數進行反分析的目標為求解一組參數值mv，cv，t0，使得目標函數值最小，隨著目標函數值接近于0，反分析結果與實際越趨于一致。求得參數值mv，cv后，可計算滲透系數k=cvγwmv。

由于目標函數為非線性函數，需要采用迭代方式對其進行求解，本模型中采用了效率較高的Newton-Raphson法[14]，并在迭代過程中沿其迭代方向進行一維搜索，確定合理的迭代步長。

(6)

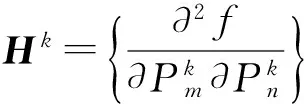
目標函數的一階導數和二階導數可表示為

(7)

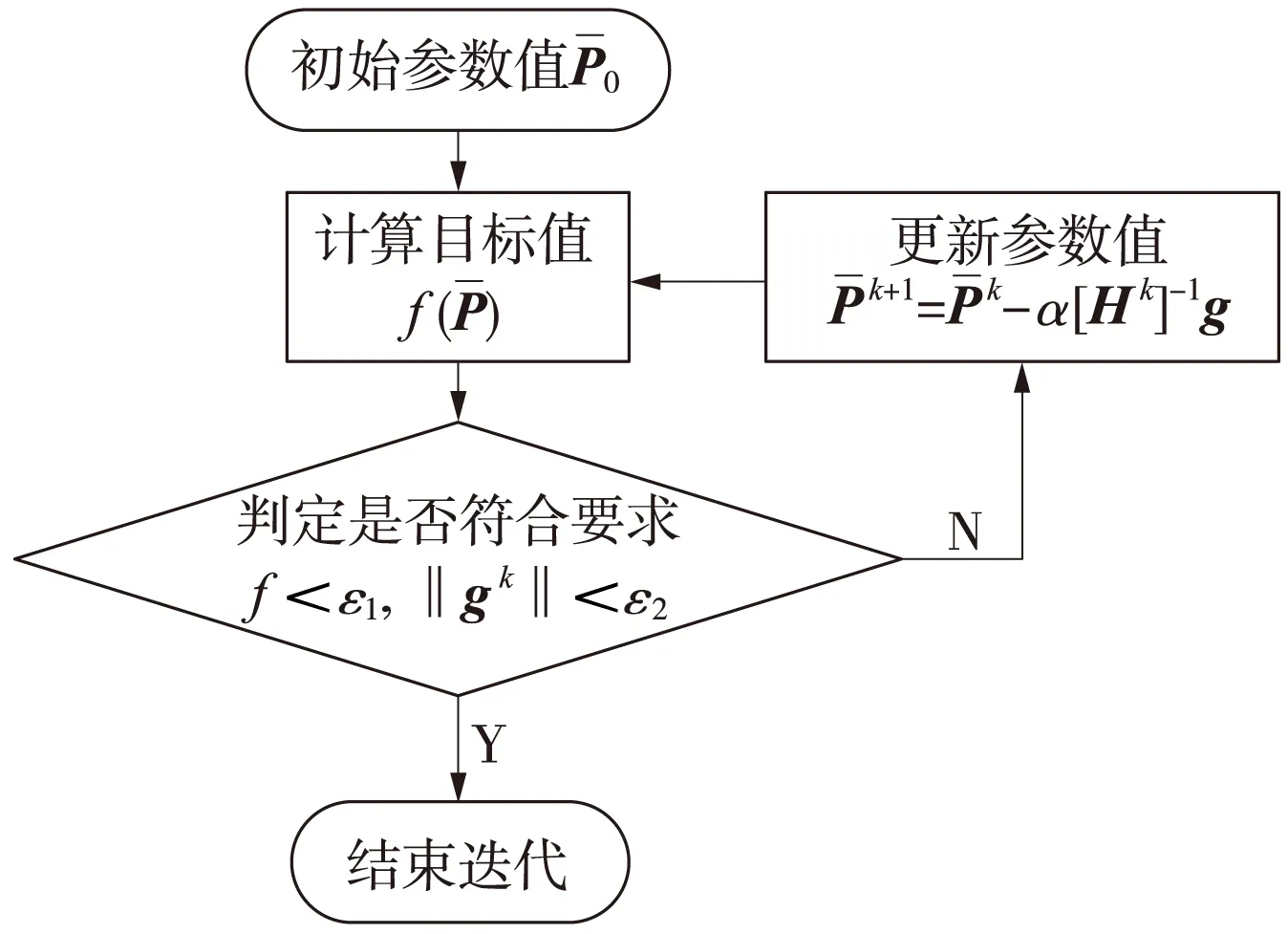
圖3　固結參數優化求解流程

3　算例分析

某地區由于超采地下水，導致地下水位發生大面積下降，下降量為20m，軟黏土層的厚度為15m，對軟黏土層沉降變形的觀測記錄如表1所示。

表1　土層沉降量監測值

假定軟黏土體積壓縮系數mv為0.1MPa-1，滲透系數k為1×10-7m/s，初始記錄時已固結時間t0為0.5d，則固結系數cv為10-4m2/s。根據沉降量監測數據對土層固結參數進行反演計算，圖4所示為目標函數值在反演過程中的變化情況。可以發現，隨著迭代過程，目標函數值迅速變小，最終接近于0，說明反分析過程是收斂的，各時間點下土層沉降計算結果與監測結果逐漸接近。

圖4　目標函數值迭代變化情況

圖5　體積壓縮系數mv迭代過程

各參數反演過程中的變化情況如圖5～圖7所示，可以看出，隨著迭代的增加，土層固結參數值逐漸趨于穩定，最終得出土層體積壓縮系數mv為0.201MPa-1，固結系數cv為9.9×10-6m2/s，初始固結時間t0為0.818d，土層滲透系數k為1.99×10-8m/s。

圖6　滲透系數k迭代過程

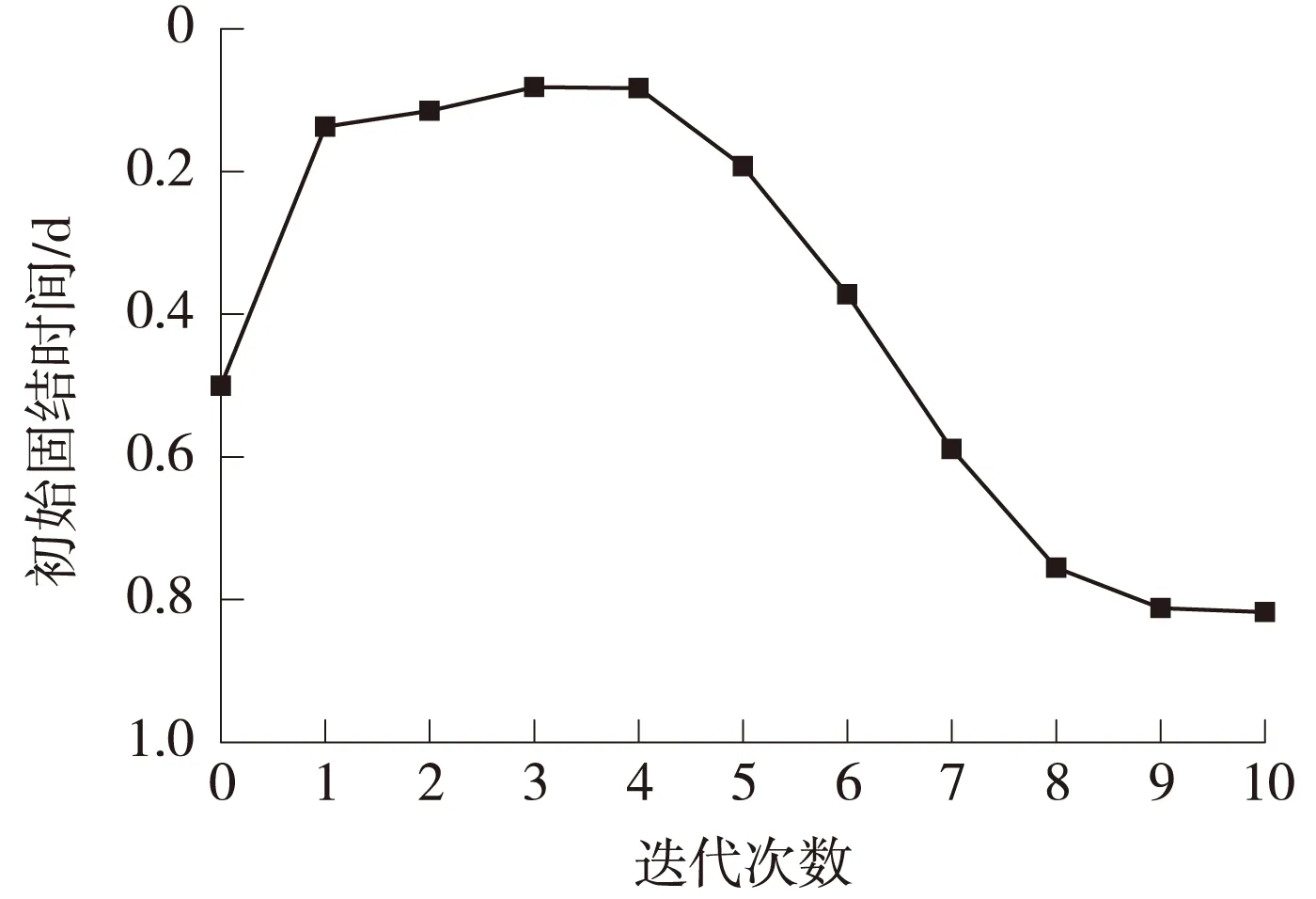
圖7　初始固結時間t0迭代過程

分別根據初始估計參數和反分析得出的土層固結參數對土層沉降變化曲線進行預測，與監測結果進行對比，如圖8所示。由圖8可以看出，由初始估計參數計算的沉降變化曲線與實際監測值差別很大，而跟據反分析參數計算的沉降變化曲線與監測值十分接近，說明反分析得出的土層固結參數是符合實際的，可以進一步用于預測以后的土層沉降變化狀況。

圖8　土層沉降變形計算曲線與監測值對比

4　結論

(1)通過對比大面積加載和地下水位下降引發的土層固結問題解析解，得出形式一致可考慮初始固結時間的土層沉降解析表達式。

(2)利用土層沉降變形監測值，建立能綜合反映各時間點下沉降監測權重的目標函數，結合土層固結解析解，利用修正Newton-Raphson方法建立固結參數反分析優化求解流程。

(3)針對具體算例對土層的固結參數進行反分析，經過10次迭代得出了符合精度要求的一組固結參數，說明反分析算法的有效性，利用該組參數值計算的土層沉降量與監測值十分接近，能夠進一步用于預測土層以后的沉降變化狀況。

[1]《工程地質手冊》編委會.工程地質手冊：第四版[M].北京:中國建筑工業出版社，2007:132-162

[2]中華人民共和國建設部.GB50021—2001巖土工程勘察規范[S].北京:中國建筑工業出版社，2009:117-119

[3]鄧永鋒，劉松玉，季署月.取樣擾動對固結系數的影響研究[J].巖土力學，2007，28(12):2687-2690

[4]李曉萍.土工試驗中常見問題探討[J].鐵道勘察，2015，41(1):78-80

[5]郗寧.三軸試件抽氣飽和方法及其對固結不排水剪強度試驗的影響分析[J].鐵道勘察，2013，39(4):39-42

[6]楊志法.巖土工程反分析的發展與展望[C]∥全國巖土工程反分析學術研討會論文集.臺州：中國巖石力學與工程學會，2006:1-11

[7]王緒鋒，解廷偉，陳炯釗，等.土體固結參數的反分析與工程應用[J].水運工程，2014(4):154-157

[8]胡榮華，余海忠，張明，等.確定軟土固結系數方法的研究[J].鐵道建筑，2010(2):74-81

[9]包太，劉新榮，朱凡，等.固結系數的最小二乘法計算[J].巖土工程學報，2005，27(10):1230-1232

[10]鄧永鋒，劉松玉，洪振舜.基于沉降資料反演固結系數的方法研究[J].巖土力學，2005，26(11):1807-1809

[11]江剛.遺傳算法在固結系數計算中的應用[J].重慶建筑大學學報，2006，28(1):50-52

[12]陳仲頤，周景星，王洪瑾.土力學[M].北京:清華大學出版社，1994:143-155

[13]駱冠勇，潘泓，曹洪，等.承壓水減壓引起的沉降分析[J].巖土力學，2004，25(增):196-200

[14]陳寶林.最優化理論與算法[M].北京:清華大學出版社，2005:287-315

Back Analysis of the Consolidation Parameters of Soil Layer Based on Analytical Solution and Modified Newton-Raphson Method

HUANG Dazhong

2016-03-24

黃大中(1987—)，男，2014年畢業于浙江大學巖土工程專業，工程師。

1672-7479(2016)04-0034-03

TU413

A