雙饋風(fēng)力發(fā)電系統(tǒng)優(yōu)化控制

劉海營　管　萍

（北京信息科技大學(xué)自動化學(xué)院，北京　100192）

?

雙饋風(fēng)力發(fā)電系統(tǒng)優(yōu)化控制

劉海營管萍

（北京信息科技大學(xué)自動化學(xué)院，北京100192）

本文雙饋風(fēng)力發(fā)電系統(tǒng)，提出了一種基于滑模理論的非線性控制方法，選擇風(fēng)力機轉(zhuǎn)速和最優(yōu)轉(zhuǎn)速的差值為滑模面，設(shè)計滑模控制器。此外，采用定子磁鏈定向的矢量控制技術(shù)，實現(xiàn)有功功率、無功功率的解耦控制。最后，根據(jù)風(fēng)力機最優(yōu)功率運行曲線，對6kW的雙饋風(fēng)力發(fā)電系統(tǒng)進行最大風(fēng)能追蹤控制研究。仿真結(jié)果表明，在給定隨機風(fēng)速情況下，風(fēng)力機能基本保持最佳葉尖速比和最大風(fēng)能利用系數(shù)，最大限度的輸出功率，實現(xiàn)最大風(fēng)能追蹤控制，減小機械載荷。

雙饋風(fēng)力發(fā)電系統(tǒng)；風(fēng)力機；最大風(fēng)能追蹤；滑模控制

為了保證雙饋風(fēng)力發(fā)電機組輸出功率最大，一般在額定風(fēng)速以下，要求風(fēng)力機保持最佳葉尖速比，才能獲得最大的氣動功率，風(fēng)速變化、槳距角的調(diào)整和葉尖速比的變化都影響風(fēng)力發(fā)電機組的輸出功率［1-2］。本質(zhì)上風(fēng)電機組的控制目標(biāo)就是通過一定的控制方法時風(fēng)輪的轉(zhuǎn)速跟隨風(fēng)速的變化，保持最佳葉尖速比，實現(xiàn)最大風(fēng)能追蹤的控制。由于風(fēng)電機組本身具有多變量、慣性大、非線性等特點，傳統(tǒng)的控制方法很難保證跟隨風(fēng)速的變化，而且風(fēng)速快速變化的情況下，嚴(yán)格跟蹤風(fēng)速又會引起較大的機械振動，對機械部件造成損害。因此，針對雙饋風(fēng)電機組非線性和風(fēng)速隨機性等特點，應(yīng)用非線性的控制方法實現(xiàn)風(fēng)電機組的最大風(fēng)能追蹤和降低機械振動是整個風(fēng)電系統(tǒng)控制研究的重點。

大多數(shù)風(fēng)能轉(zhuǎn)換系統(tǒng)采用的發(fā)電機類型主要有雙饋感應(yīng)發(fā)電機、自勵式發(fā)電機、永磁同步發(fā)電機。本文采用雙饋發(fā)電機，因為其具有如下優(yōu)點：首先，能在較大的風(fēng)速范圍內(nèi)正常運行；其次，能產(chǎn)生恒頻的有功功率；最后，能實現(xiàn)有功功率、無功功率的解耦控制。

滑模控制的“滑動模態(tài)”可以進行設(shè)計且與對象參數(shù)及擾動無關(guān)，因此，滑模控制具有快速響應(yīng)、對參數(shù)變化及擾動不靈敏、無需系統(tǒng)在線辨識、實現(xiàn)簡單等優(yōu)點，確保狀態(tài)軌跡在期望的滑模面附近運動。對雙饋風(fēng)力發(fā)電系統(tǒng)最大風(fēng)能跟蹤來講，正是需要系統(tǒng)運行在最佳功率曲線上，因而滑模控制正好成為有效的工具。

本文通過轉(zhuǎn)速控制方法優(yōu)化風(fēng)力發(fā)電系統(tǒng)輸出最優(yōu)轉(zhuǎn)矩，最后以6kW雙饋風(fēng)力發(fā)電系統(tǒng)為研究對象，進行最大風(fēng)能追蹤的仿真研究。

1　雙饋風(fēng)電系統(tǒng)模型

雙饋風(fēng)力發(fā)電系統(tǒng)的結(jié)構(gòu)圖如圖1所示。雙饋電機的定子直接連接電網(wǎng)，轉(zhuǎn)子通過三相勵磁變換器進行交流勵磁，從而使電磁功率通過定轉(zhuǎn)子兩個回路與電網(wǎng)進行交換。從整個系統(tǒng)來看，可以被分成兩個相對獨立的子系統(tǒng)，分別是空氣動力學(xué)系統(tǒng)（包括風(fēng)力機和齒輪箱）和電氣子系統(tǒng)（雙饋電機）。

圖1　雙饋風(fēng)力發(fā)電系統(tǒng)結(jié)構(gòu)圖

2　發(fā)電機模型

對于雙饋發(fā)電機，定、轉(zhuǎn)子分別選取發(fā)電機與電動機慣例，在d、q兩相同步速旋轉(zhuǎn)坐標(biāo)系下，電壓和磁鏈方程分別為［3］

電磁轉(zhuǎn)矩方程為

定子端有功功率、無功功率方程為

式中，s、r分別代表定、轉(zhuǎn)子側(cè)變量；d、q分別代表同步旋轉(zhuǎn)坐標(biāo)系的坐標(biāo)軸；u、i、ψ分別代表電壓、電流和磁鏈；R、L分別代表電阻和電感值；np代表極對數(shù)；P、Q代表有功功率和無功功率；ω0、ωs分別代表同步角速度和轉(zhuǎn)差角速度。

為了簡化后續(xù)控制器的設(shè)計，采用定子磁鏈定向的矢量控制方法，對有功功率、無功功率實現(xiàn)解耦控制。將定子磁鏈的矢量ψs定向在d軸上時，有

當(dāng)電機穩(wěn)定運行時，定子磁鏈保持恒定，忽略定子電阻sR，則有

式中，a=Rr，，c=Lmψs/Ls。

此時電磁轉(zhuǎn)矩簡化為

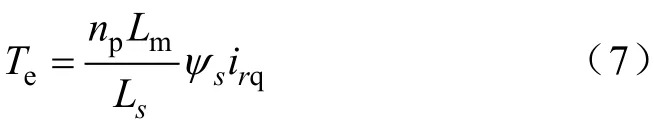
定子端有功功率、無功功率簡化為

可見，Ps，Qs分別與轉(zhuǎn)子電流的轉(zhuǎn)矩分量 irq和勵磁分量idr成線性關(guān)系，通過調(diào)節(jié)兩個電流的分量就可以獨立地調(diào)節(jié)有功功率、無功功率，進而實現(xiàn)解耦控制。

3　風(fēng)力機模型

風(fēng)力機是風(fēng)力發(fā)電系統(tǒng)中能量轉(zhuǎn)換的首要環(huán)節(jié)，能將截獲的流動空氣產(chǎn)生的動能轉(zhuǎn)化為機械能，對整個風(fēng)力發(fā)電系統(tǒng)的輸出功率影響較大，直接影響整個風(fēng)力發(fā)電機組的穩(wěn)定運行、安全可靠性能等。

根據(jù)空氣動力學(xué)的相關(guān)知識，可以推導(dǎo)出風(fēng)力機捕獲風(fēng)能的功率為［4］

式中，ρ為空氣密度；v為外界風(fēng)速；Cp為風(fēng)能利用系數(shù)；β為槳距角；λ為葉尖速比，葉尖速比為葉片尖端線速度與風(fēng)速之比，且滿足：

式中，ω為風(fēng)力機葉輪角速度，R為風(fēng)力機葉輪半徑。

風(fēng)能利用系數(shù) Cp是表征風(fēng)力機轉(zhuǎn)換效率的重要參數(shù)，本身與風(fēng)速和風(fēng)力機設(shè)計的參數(shù)有關(guān)系，本文選用常用的風(fēng)能利用系數(shù)經(jīng)驗式為［5］

風(fēng)能轉(zhuǎn)換系統(tǒng)的運動方程為［6］

式中，J和 B是整個發(fā)電機側(cè)總的轉(zhuǎn)動慣量和摩擦系數(shù)；Tmec是齒輪箱輸出的機械轉(zhuǎn)矩也即是發(fā)電機的輸入轉(zhuǎn)矩；Te是發(fā)電機的電磁轉(zhuǎn)矩；ωr是發(fā)電機的機械角速度。

因為風(fēng)力機和發(fā)電機是通過增速齒輪箱聯(lián)系在一起的，如果忽略傳動過程中的各種損耗，則風(fēng)輪機角速度和發(fā)電機角速度，風(fēng)力機吸收的機械轉(zhuǎn)矩和發(fā)電機的輸入轉(zhuǎn)矩滿足的關(guān)系式如下：

式中，G為增速齒輪箱的傳動比，wT為風(fēng)力機轉(zhuǎn)化風(fēng)能得到的機械轉(zhuǎn)矩。

4　最大風(fēng)能追蹤原理

由式（10）可知，假定發(fā)電機轉(zhuǎn)速保持恒定值不變，當(dāng)外界風(fēng)速發(fā)生變化時，葉尖速比也會隨之改變，從而導(dǎo)致風(fēng)能利用系數(shù)一直變化，最后風(fēng)輪機輸出的功率也在一直變化，而并不是一直以最大功率輸出。

一個特定的定槳距風(fēng)力機具有唯一的可使Cp達(dá)最大值的葉尖速比，稱為最佳葉尖速比λopt，其對應(yīng)的Cp為最大風(fēng)能利用系數(shù)Cpmax。從圖2中可知，當(dāng)β=0時對應(yīng)的最大風(fēng)能利用系數(shù)Cpmax=0.45，此時對應(yīng)得出最佳葉尖速比λoptimal。

當(dāng)外界風(fēng)速不斷變化時，不斷調(diào)整發(fā)電機轉(zhuǎn)速，使葉尖速比維持在一個最優(yōu)值λopt，所以此時風(fēng)能利用系數(shù)Cp也是維持在最大值Cpmax，保證風(fēng)力發(fā)電系統(tǒng)能產(chǎn)生最大的風(fēng)能。

這天蔣利學(xué)也很愜意，他愜意的原因是這天上午的學(xué)術(shù)報告做的非常成功。做完報告，主席臺上下響起了一片經(jīng)久不息的掌聲。以前他也多次參加過類似的學(xué)術(shù)研討會，也上主席臺做過報告，做完報告，也獲得了一片贊譽，一片掌聲。但那些贊譽和掌聲遠(yuǎn)沒有今天的贊譽和掌聲來的激烈，尤其是在國家衛(wèi)生部有關(guān)領(lǐng)導(dǎo)的帶領(lǐng)下，掌聲愈發(fā)顯得熱烈，也愈發(fā)顯得經(jīng)久不息。研討會結(jié)束，衛(wèi)生部領(lǐng)導(dǎo)還在省廳和市局主要領(lǐng)導(dǎo)陪同下接見了蔣利學(xué)，并在會見后親切地和他留影留念。

根據(jù)最大風(fēng)能跟蹤理論，推導(dǎo)出發(fā)電機最優(yōu)轉(zhuǎn)速參考值為

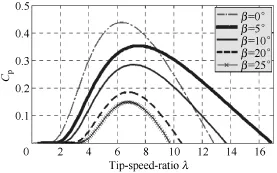
圖2　風(fēng)能利用系數(shù)和葉尖速比、槳距角關(guān)系

5　滑模控制器設(shè)計

5.1滑模控制理論

滑模變結(jié)構(gòu)控制是變結(jié)構(gòu)控制系統(tǒng)的一種控制策略，這種控制策略與常規(guī)控制的根本區(qū)別在于控制的不連續(xù)性，即具有一種使系統(tǒng)“結(jié)構(gòu)”隨時間變化的開關(guān)特性。該控制特性可以迫使系統(tǒng)在一定特性下沿規(guī)定的狀態(tài)軌跡作小幅度、高頻率的上下運動，即所謂的滑動模態(tài)或“滑模”運動。這種滑動模態(tài)是可以設(shè)計的，且與系統(tǒng)的參數(shù)及擾動無關(guān)，這樣，處于滑模運動的系統(tǒng)就具有很好的魯棒性。

針對如下非線性控制系統(tǒng)進行設(shè)計［7］：

式中，x∈?n是狀態(tài)矢量，f（x，t）∈?n，B（x，t）∈?n× m，u∈?m是控制矢量。由式（14）所示的被控系統(tǒng)，可設(shè)滑模面S滿足以下表達(dá)式：

要使?fàn)顟B(tài)變量在滑模面上運動，必須滿足如下兩個條件：

該控制率滿足的先決條件是控制器為如下形式：

由式（17）知：

設(shè)定Lyapunov函數(shù)為

根據(jù)Lyapunov穩(wěn)定性理論，保證滑模控制的全局收斂和穩(wěn)定性，需滿足以下表達(dá)式：

本文設(shè)計控制器采用如下形式的滑模面：

式中，e（x）是誤差矢量（e（x）=x*?x），λx是一個正常數(shù)，n是系統(tǒng)的階數(shù)。

5.2滑模控制器設(shè)計

為了設(shè)計滑模變結(jié)構(gòu)的速度控制器，將式（12）變形為

選取發(fā)電機轉(zhuǎn)速誤差函數(shù)作為滑模面函數(shù)，表達(dá)式為

滑模面的導(dǎo)數(shù)為

滑模控制器的設(shè)計時，除了保證在正常運動段滑動模態(tài)的可達(dá)性，最好還要改善在這段運動的動態(tài)品質(zhì)，在一定程度上，可以用規(guī)定“趨近律”的方法來加以控制。本文選取如下指數(shù)趨近律：

式中，0ε＞，0k＞，上式后半部分為指數(shù)趨近項，當(dāng)S較大時，系統(tǒng)能以較大的速度趨近于滑動模態(tài)，但是單純的指數(shù)趨近，運動點在逼近切換面的時候只是一個漸近的過程，不能保證在有限時間內(nèi)到達(dá)，所以增加一個等速趨近項，當(dāng)S趨近于零時，趨近速度為ε而非零，可以保證在有限時間內(nèi)到達(dá)。

由式（19）至式（21）的證明過程可知，應(yīng)用到本控制器中，能保證，所以設(shè)計控制是穩(wěn)定的。

由式（14）、式（23）、式（25）和式（26）可推導(dǎo)出最優(yōu)轉(zhuǎn)矩的參考值為

6　仿真

風(fēng)力機參數(shù)：葉片半徑R=2.5m，空氣密度為1.25kg/m3，最大風(fēng)能利用率0.48，最佳葉尖速比λ=7，齒輪箱增速比Kg=6.25，額定功率6kW，機械傳動效率η=0.95，系統(tǒng)時間常數(shù)為0.2s，風(fēng)輪轉(zhuǎn)動慣量Jw=3kg? m2

雙饋感應(yīng)發(fā)電機參數(shù)：額定功率6kW，發(fā)電機極對數(shù) np=2，發(fā)電機時間常τg=0.2，發(fā)電機額定電壓220V，定子電阻 Rs=1.265，轉(zhuǎn)子電阻Rr=1.430，定子電感 Ls=0.1452，轉(zhuǎn)子電感Lr=0.1452，定轉(zhuǎn)子互感 Lm=0.1397，發(fā)電機轉(zhuǎn)動慣量Jg=0.01kg? m2。

為檢驗控制器的效果，整個雙饋風(fēng)力發(fā)電系統(tǒng)在隨機風(fēng)速作用下進行仿真研究，輸入的隨機風(fēng)速曲線如圖3所示。在此風(fēng)速下，要求風(fēng)力機轉(zhuǎn)速能跟隨風(fēng)速變化，保持最佳葉尖速比運行，使輸出功率在最佳運行區(qū)間，實現(xiàn)最大風(fēng)能追蹤控制。仿真時間設(shè)定為40s。

圖3　風(fēng)速仿真曲線

由圖4和圖5的對比可知，在滑模控制作用下的雙饋風(fēng)力發(fā)電系統(tǒng)，葉尖速比基本維持在最優(yōu)值7附近，無較大波動。圖6和圖7風(fēng)能利用系數(shù)的對比再次驗證滑模控制器的控制效果更好。圖8和圖9表明，在隨機風(fēng)速變化的情況下，滑模控制能使風(fēng)力機更好的跟隨風(fēng)速的變化，實現(xiàn)最大風(fēng)能跟蹤控制。

圖4　傳統(tǒng)PID控制

圖5　滑模控制

圖6　傳統(tǒng)PID控制

圖7　滑模控制

圖8　傳統(tǒng)PID控制

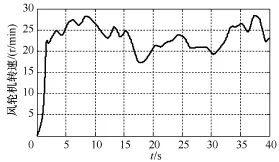
圖9　滑模控制

7　結(jié)論

通過對6kW雙饋風(fēng)力發(fā)電系統(tǒng)的仿真研究，本文提出的非線性最大風(fēng)能追蹤控制方法，相比于傳統(tǒng)的PID控制，實現(xiàn)了風(fēng)力發(fā)電系統(tǒng)的優(yōu)化運行，保證了系統(tǒng)能快速跟隨外界風(fēng)速的變化，維持最佳葉尖速比，使整個風(fēng)電機組運行在最優(yōu)區(qū)域，實現(xiàn)了最大風(fēng)能追蹤控制。

［1］ 鐘沁宏，阮毅，趙梅花，等. 變步長爬山法在雙饋風(fēng)力發(fā)電系統(tǒng)最大風(fēng)能跟蹤控制中的應(yīng)用［J］. 電力系統(tǒng)保護與控制，2013，41（9）︰67-73.

［2］ 付明曉，李守智. 變速恒頻風(fēng)力發(fā)電系統(tǒng)最大風(fēng)能追蹤的控制［J］. 電力系統(tǒng)及其自動化學(xué)報，2013，25（1）︰74-78.

［3］ 張鳳，閻秀恪，蘭宏光，等. 基于滑模控制的風(fēng)機最大風(fēng)能追蹤［J］. 沈陽工業(yè)大學(xué)學(xué)報，2014，36（6）︰625-630.

［4］ 秦斌，周浩，邱麗，等. 基于模糊滑模控制的風(fēng)力發(fā)電系統(tǒng)最大風(fēng)能追蹤［J］. 上海交通大學(xué)學(xué)報，2014，48（7）︰993-997，1003.

［5］ 鄭雪梅，李琳，徐殿國. 雙饋風(fēng)力發(fā)電系統(tǒng)最大風(fēng)能追蹤滑模變結(jié)構(gòu)控制［J］. 控制理論與應(yīng)用，2010，27（7）︰923-926.

［6］ 顏康. 變速恒頻雙饋風(fēng)力發(fā)電機的最大風(fēng)能跟蹤控制［D］. 沈陽︰沈陽工業(yè)大學(xué)，2015.

［7］ 王豐堯. 滑模變結(jié)構(gòu)控制［M］. 北京︰機械工業(yè)出版社，1995.

Optimal Control of Doubly Fed Induction Generator Systems

Liu HaiyingGuan Ping
（School of Automation，Beijing Information Science and Technology University，Beijing100192）

A nonlinear control method based on the sliding mode theory is presented for the doubly fed wind power generation system. The difference between the speed and the optimal speed of the wind turbine is selected as the sliding mode controller. In addition，the control system adopts the vector control technology of stator flux orientation，and realizes the decoupling control of active power and reactive power. Finally，according to the wind turbine optimal power curve，doubly fed wind power generation system of 6kW for maximum wind power tracking control is studied. Simulation results show that the under the given stochastic wind speed，wind turbine remained optimal tip speed ratio and the maximum wind energy utilization coefficient，achieving the maximum output power and maximum power point tracking control，reducing the mechanical load.

double-fed induction generator system； wind turbines； maximum power point tracking control； sliding model control

劉海營（1988-），男，漢族，河北唐山人，主要研究方向：智能非線性控制在雙饋風(fēng)力發(fā)電系統(tǒng)中應(yīng)用。