一類常系數非齊次線性微分方程特解的求法

周志穎

（荊州理工職業學院 基礎課部，湖北 荊州 434000）

一類常系數非齊次線性微分方程特解的求法

周志穎

（荊州理工職業學院 基礎課部，湖北 荊州 434000）

針對n階常系數非齊次線性微分方程運用特征函數導數法和比較系數法，得到了方程的一個公式化特解，簡單易行。

n階常系數非齊次線性微分方程；特征根；特解

近年來，微分方程在實際問題中應用越來越廣泛，微分方程理論的研究也引起國內外學者的關注。線性微分方程的解作為微分方程的基礎，梁樹生等[1-5]對其解的結構以及求解方法進行了詳盡的描述。龔東山等[6]介紹了n階常系數非齊次線性微分方程

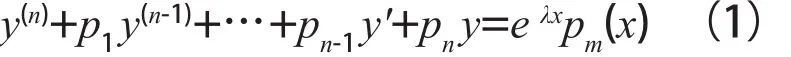
特解的求法，本文將介紹n階常系數非齊次線性微分方程

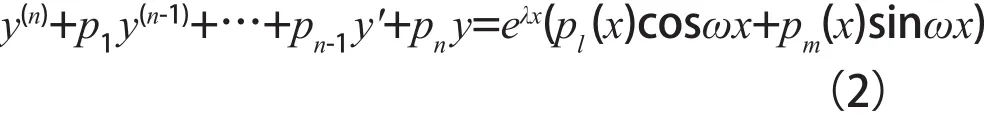
1　預備知識

n階常系數非齊次線性微分方程（2）對應的齊次線性微分方程為

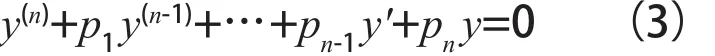
若r為方程（3）的根，由[4]可得如下定義：

定義1：稱

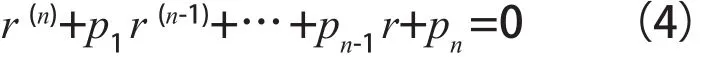
為方程（3）的特征方程。稱

為方程（2）的特征函數。

由導數的相關性質[7]可得：

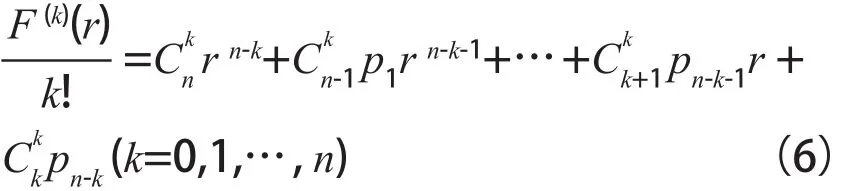
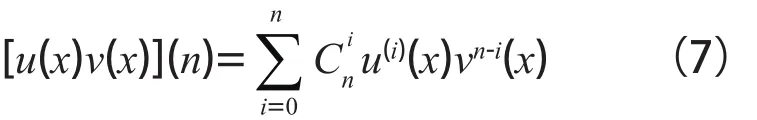
其中u(x)和v(x)均為x的n次可微函數。

2　主要定理

定理：n階常系數非齊次線性微分方程（2）存在特解：

其中k(k=0, 1, …n)表示λ+iω（或λ-iω）為特征方程（4）的根的重數。

證明：n階常系數非齊次線性微分方程（2）可表示為指數形式[3]129-130：

互為共軛。

由非齊次線性微分方程的疊加原理[3]112：

的解之和必為方程（8）的解。

現求方程（9）的特解。將Pl(x)與Pm(x)代入方程（9）得：

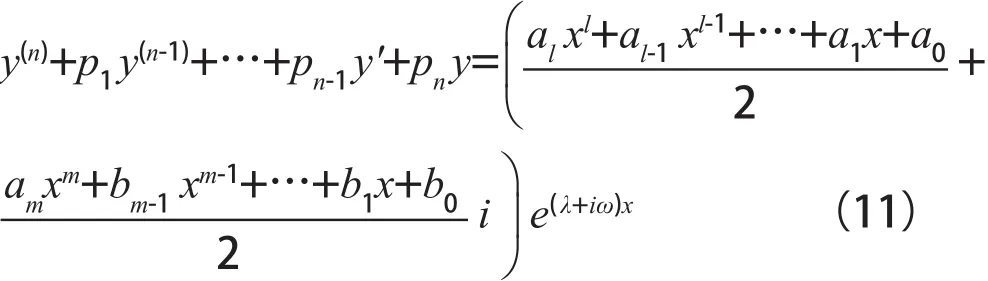
假定方程（11）有特解：

①當λ+iω不是方程（4）的特征根時，有F( j)(λ+iω) ≠0（j=0, 1,…n），通過觀察及比較方程（12）等式兩邊系數，可得到：

②當λ+iω是方程（4）的k重特征根時，有

F (λ+iω)=F′(λ+iω)=…F(k-1)(λ+iω)=0，F(k)(λ+iω) 10，將 F( j)(λ+iω)（j=0, 1,…n）帶入方程（12），得：

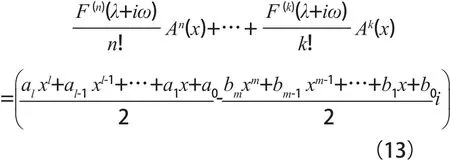
比較方程（13）等式兩邊系數，可得：

綜合①、②可得方程（9）的特解為：

其中k表示λ+iω（或λ-iω）為方程（4）的k重特征根。

其中k表示λ+iω（或λ-iω）為方程（4）的k重特征根。

由非齊次線性微分方程的疊加原理[3]112可得，方程（8）的特解為:

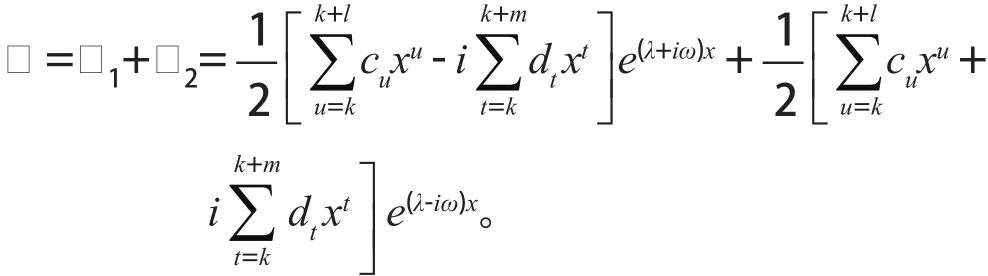
由復數的相關性質[8]可得：

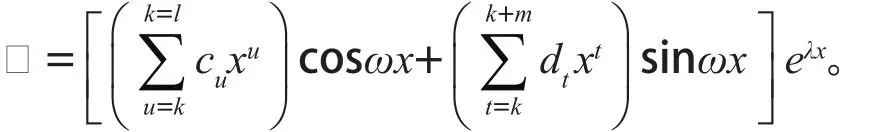
其中k表示λ+iω（或λ-iω）為方程（4）的k重特征根。證畢。

3　實例

例1求微分方程y′-2y′+5y=exsin2x的特解。

解：由題意可知λ=1，ω=2，l=0， m=0，又微分方程的特征根為r1=1+2i、r2=1-2i，所以λ+iω=2+2i是特征方程的單根，即k=1，由定理可得方程的特解為：

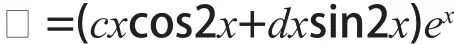
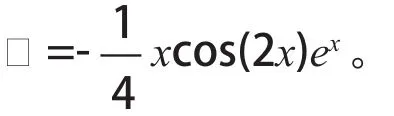
例2求微分方程y′′′-y=cosx的特解。

解：由題意可知λ=0，ω=1，l=0， m=0，又微分方程的特征根為，所以λ+iω=i不是特征方程的根，即k=0，由定理可得方程的特解為：

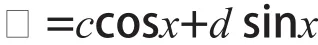
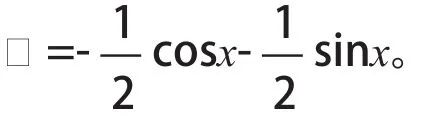
[1] 梁樹生．高等數學（下冊）[M].武漢：華中師范大學出版社，2010：137-169.

[2] 阮炯.常微分方程方法導引[M].上海：復旦大學出版社，1991：2-14.

[3] 王高雄，周之銘，朱思銘，等．常微分方程[M].2版.北京：高等教育出版社，1983.

[4] 孫清華，李金蘭，孫昊．常微分方程內容、方法與技巧[M].武漢：華中科技大學出版社，2006：137-215.

[5] 華東師范大學數學系．數學分析（下冊）[M].3版.北京：高等教育出版社，2002.

[6] 龔東山，劉岳巍．一類常系數線性微分方程特解的求法[J].高等數學研究，2010（4）：58-60.

[7] 同濟大學應用數學系.高等數學（上冊）[M].5版.北京：高等教育出版社，2002：76-124.

[8] 鐘玉泉.復變函數[M].第二版.北京：高等教育出版社，2001：3-16.

A Particular Solution to the Kind of Non-homogeneous Linear Differential Equations with Constant Coeffi cients

ZHOU Zhiying
(Department of Basic Courses, Jingzhou Vocational and Technical College, Jingzhou Hubei 434000, China)

The eigenfunction derivative method and comparison coeffi cient method can be applied to the n-order non-homogeneous linear differential equation with constant coeffi cients, y(n)+p1y(n-1)+…+pn-1y′+pny=eλx(p1(x)cosωx+ pm(x)sinωx), and a formulable specifi c solution is obtained, which is simple and easy.

the n-order non-homogeneous linear differential equation with constant coeffi cients; characteristic root; a specifi c solution.

O175

A

1674 - 9200（2016）03 - 0036 - 03

（責任編輯劉常福）

2015 - 10 - 18

周志穎，男，湖北天門人，荊州理工職業學院基礎課部講師，碩士，主要從事數學教育研究。