負載模擬器彈性桿的結構優化與有限元分析

楊瑞峰，劉志凱，郭晨霞，張　鵬

（1.中北大學儀器與電子學院，山西 太原 030051；2.中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原 030051）

負載模擬器彈性桿的結構優化與有限元分析

楊瑞峰1，2，劉志凱1，2，郭晨霞1，2，張鵬1，2

（1.中北大學儀器與電子學院，山西 太原 030051；2.中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原 030051）

為提高電動負載模擬器中彈性桿的性能，對其進行結構優化與有限元分析。根據扭轉強度條件，確定彈性桿的最小直徑；根據電動負載模擬器的加載梯度，對彈性桿的長度進行優化設計；以減小彈性桿所受應力為原則，運用零階優化算法對過渡圓角半徑進行優化設計，得到最優解。利用ANSYS軟件對彈性桿進行模態和疲勞壽命的有限元分析，仿真結果表明彈性桿的固有頻率和疲勞壽命滿足電動負載模擬器的使用要求。研究結果對彈性桿在電動負載模擬器中充分發揮作用以及進一步的優化設計具有指導意義。

電動負載模擬器；彈性桿；結構優化設計；模態分析；疲勞壽命分析

0　引　言

電動負載模擬器主要是對舵機進行力矩加載試驗，并模擬舵機在飛行過程中所受空氣動力載荷，對舵機的性能進行全方位的反復測試，獲得相應的實驗數據，以此判斷舵機性能的好壞［1-2］。因此，電動負載模擬器的性能直接影響舵機的性能，從而影響飛行器的性能。由于存在加載控制誤差，電動負載模擬器中力矩電機輸出的力矩不可能完全等于期望力矩，兩者之間的誤差即為系統的多余力矩［3］。在電動負載模擬器中引入彈性桿能有效減少多余力矩對電動負載模擬器系統的影響，減少加載轉矩的高頻分量，利于提高動態加載力矩控制的穩定性［4］。因此，彈性桿性能的好壞直接關系到電動負載模擬器性能的好壞。彈性桿在工作過程中主要承受交變扭轉載荷的作用，另外，由于結構設計的需要，不可避免地引入軸肩、軸環等，這些位置在外載荷作用下會引起應力集中，這些因素都會使彈性桿發生疲勞破壞，影響彈性桿的使用壽命和性能。此外，引入彈性桿可能使得系統整體發生共振，對系統造成破壞。因此，對彈性桿結構進行優化設計，并分析其模態和疲勞壽命對于彈性桿在電動負載模擬器中的應用具有重要意義。

1　電動負載模擬器簡介

電動負載模擬器的結構如圖1所示，其中，工裝軸、法蘭盤構成扭矩傳遞機構，力矩電機作為電動負載模擬器的執行機構，為系統提供加載力矩，在動態加載試驗中，舵機做主動運動，負載模擬器跟隨舵機運動，同時進行力矩加載。加載的力矩對于舵機而言是阻力矩，即與舵機的運動方向相反。扭矩傳感器和光電編碼器分別測量負載扭矩和舵機的偏轉角。在力矩電機與舵機的連接環節中采用彈性桿作為緩沖機構，能夠降低負載模擬器的連接剛度和多余力矩，提高負載模擬器的性能。

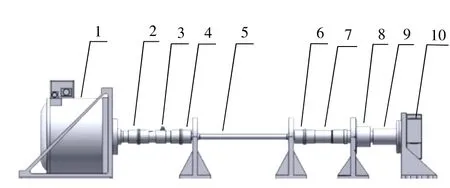
圖1　電動負載模擬器結構圖

2　彈性桿的結構優化設計與建模

2.1彈性桿的初始結構設計

目前，在彈性桿制作中，應用廣泛的材料是40Cr，其彈性模量E=200 GPa，泊松比μ=0.3，屈服極限［S］=392.5 MPa，扭轉切應力［］=196.2 MPa，切變模量G=76923.1MPa。

在電動負載模擬器中，彈性桿只受到扭矩作用，扭矩T=400N·m，有：

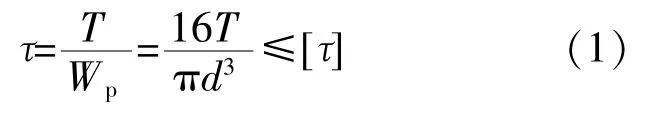
則彈性桿的最小許用直徑d為

由圖1可知彈性桿的左右兩端分別與標準件聯軸器2和聯軸器3連接。彈性桿應力集中的主要部位為軸肩或過渡圓角處。徑比越大，階梯軸截面形狀過度劇烈，階梯軸過渡圓角處的應力集中系數增加，彈性桿的疲勞壽命變短［5］。因此，根據所選聯軸器的型號以及由式（1）得出的d值來確定彈性桿左右兩端的直徑和長度分別為d1=28 mm，l1=50 mm；d3= 28 mm，l3=50mm；過渡圓角半徑初定為3mm。

2.2彈性桿的優化設計

2.2.1彈性桿長度的優化設計

圓軸剛度系數的計算公式為

設彈性桿左端的剛度系數為KL1，中間部分的剛度系數為KL2，右端的剛度系數為KL3，則：

對于變直徑的彈性桿，其總體的剛度系數為

加載梯度表示舵機承受的負載與舵機轉角之間的函數關系，當彈性桿剛度系數略大于系統加載梯度時，彈性桿在電動負載模擬器中能充分發揮作用，提高負載模擬器系統的整體性能［6］。本文電動負載模擬器的加載梯度為30～80（N·m）/（°），因此，選擇彈性桿的剛度系數KL為83（N·m）/（°），進而得到l2的值為395.01mm，圓整為396mm。

2.2.2彈性桿過渡圓角的優化設計

1）優化算法的選擇

在ANSYS中優化算法有零階方法和一階方法。零階方法使用罰函數法（SUPT），能把一般約束優化問題轉化為非約束優化問題進行求解，并且最小二乘擬合曲線可用來表達目標函數和約束函數。一階方法的原理同零階方法一樣，但是一階方法使用的不是目標函數和約束函數的值，而是使用其偏導數。在優化過程中，許多函數不容易求解導數［7］。因此，選擇零階方法對彈性桿的過渡圓角半徑進行優化設計。

零階方法的公式為

式中：H——目標函數或狀態變量的近似值；

Xn——設計變量；

a、b、c——系數；

N——設計變量總數。

利用加權最小二乘法，獲取系數bn和cnm的值，然后可以得到曲線擬合形式的目標函數和約束函數。最后進行迭代，算出目標函數的極值。

2）優化設計

將彈性桿的過渡圓角半徑設為設計變量，變化范圍為3～8mm，收斂誤差取0.001；目標函數取過渡圓角處的最大應力為最小，即：

式中：（xi，yi，zi）——過渡圓角區域內任意點的坐標；

σ（xi，yi，zi）——坐標點上的應力，收斂誤差為

0.01。

在ANSYS中，必須對模型參數化建模才能優化分析，因此利用APDL語言，以設計變量作為參數建立彈性桿的參數化模型。

迭代12次后收斂得到過渡圓角處的半徑-應力曲線如圖2所示。

圖2　半徑-應力曲線圖

由圖可知，過渡圓角處的應力隨著半徑的逐漸增大而降低，但是考慮到彈性桿的加工工藝，加工過大的過渡圓角半徑比較困難，因此選擇過渡圓角半徑為5mm，此時彈性桿受到的最大應力為349.6MPa，低于材料的屈服極限392.5 MPa，即滿足使用要求，也便于加工。

3　彈性桿的有限元分析

3.1彈性桿的模態分析

3.1.1模態分析理論

模態分析的基本思路是：將系統振動微分方程中的物理坐標變換為模態坐標，使方程組解耦，求出系統的模態參數［8］，其運動方程為

式中：M、K——系統質量矩陣和剛度矩陣；

x——系統的坐標矢量。

結構的自由振動為簡諧振動，位移為正弦函數，即x=xsinωt，將其帶入運動方程得：

該方程的特征值對應的特征向量為結構自振下對應的振型。

3.1.2模態分析及結果分析

若電動負載模擬器在工作中發生共振現象會對負載模擬器中的各零部件造成十分嚴重的損害。因此，有必要對彈性桿進行模態分析，確定其固有頻率；此外，通常電動負載模擬器的扭矩傳遞機構并沒有彈性桿，引入彈性桿使得系統的扭矩傳遞機構發生了改變，扭矩傳遞機構的固有頻率也發生了變化，對扭矩傳遞機構也有必要進行模態分析，防止發生共振。電動負載模擬器作為一個被動加載系統，是由電機驅動的舵軸帶動轉動的，該電機的工作頻率為0～300Hz。

1）在ANSYS模態分析中，網格劃分方法的選擇以及疏密程度直接影響到仿真結果的精度和正確性，對于軸類零件選用Sweep法，即掃掠法能夠得到較好的網格。因此，在對彈性桿進行網格劃分時，設置全局單元尺寸為3mm，對整體進行掃掠網格劃分，為了得到更高質量的網格，再對過渡圓角進行細化處理，Refinement設置為2mm，最終得到彈性桿的網格劃分圖如圖3所示，共有71024個節點，43246個單元。

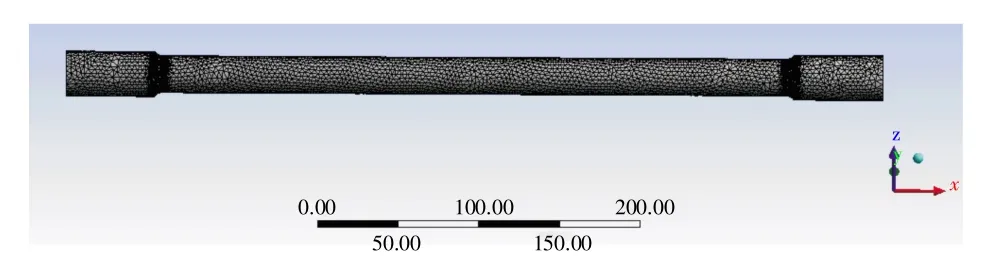
圖3　彈性桿的網格劃分圖（單位：mm）

對彈性桿單獨進行模態分析。根據彈性桿的實際工作情況，對彈性桿的右端面施加固定約束，左右兩端分別施加圓柱面約束，使彈性桿只能轉動不能徑向和軸向擺動。通常情況下，低階振型對結構的動態特性影響較為明顯，因此，求得彈性桿在上述情況下的1～6階固有頻率如表1所示。

表1　彈性桿的1～6階固有頻率

由表可知，彈性桿在約束狀態下的最小固有頻率為636.43Hz，遠遠超出電機的最大工作頻率，這表明彈性桿在正常工作頻率下不會發生共振，不會影響到電動負載模擬器的性能。

2）對扭矩傳遞機構進行模態分析。對于復雜的機構，必須對其進行簡化處理來提高分析效率。對機構中的鍵槽以及孔按實體處理以提高分析效率；在接觸選項中將聯軸器與彈性桿接觸地方簡化為綁定，法蘭盤與工裝軸接觸地方也簡化為綁定。在約束的施加中，由于支架是通過軸承來支撐和固定彈性桿的，因此在軸承與彈性桿接觸地方施加圓柱面約束，對彈性桿的右端面施加固定約束，約束機構的軸向和徑向位移。在網格劃分過程中，考慮到機構的零部件比較多，所需計算時間以及計算機性能等因素，本文對系統整體進行網格劃分時采用Element size為5mm。網格劃分后得到其網格劃分如圖4所示。其節點數目為75792，單元為35469。

圖4　扭矩傳遞機構的網格劃分圖（單位：mm）

設置好邊界條件以后，得到系統整體的1～6階固有頻率如表2所示。

表2　扭矩傳遞機構的1～6階固有頻率

由表可知，扭矩傳遞機構加入彈性桿后的最小固有頻率為334.68 Hz，超出電機的最大工作頻率。這表明在電動負載模擬器中使用彈性桿不會引起共振，因此可以在電動負載模擬器中引入彈性桿。

3.2彈性桿的疲勞壽命分析

由于彈性桿是在交變載荷作用下工作，因此疲勞破壞是其失效的主要形式。在疲勞斷裂時，彈性桿不會發生明顯的宏觀塑性變形，突然發生斷裂往往會導致災難性的事故［9］。因此，應對彈性桿進行疲勞壽命分析，防止其發生突然斷裂，造成不可挽救的損失。在電動負載模擬器的設計要求中，對系統疲勞壽命的要求是≥1萬次。

材料的應力壽命曲線常用S-N曲線來表示，S-N曲線可表示為冪指數形式［10］，即：

式中：N——疲勞壽命；

S——變載荷下的應力；

m、C——與材料屬性、應力比和力加載方式等

有關的參數。

將彈性桿的模型導入到ANSYS中，并添加材料劃分網格，Element size設置為5mm，負載為400N·m，頻率為0.3Hz，求解壽命和損傷，得到彈性桿的應力壽命曲線如圖5所示，損傷云圖如圖6所示。

由圖5可知，在最大應力349.6MPa下彈性桿的疲勞壽命為12359周次；由圖6可知彈性桿中間部分在應力循環41 831周次才比較容易發生疲勞斷裂，均超過設計要求的10000周次，滿足使用要求。在實際應用中，彈性桿在大部分時間里受到的扭矩均小于400N·m，所以彈性桿在實際應用中的疲勞壽命遠遠大于仿真分析結果。

圖5　彈性桿應力壽命曲線圖

圖6　彈性桿損傷云圖

4　結束語

本文以提高電動負載模擬器整體性能、減小彈性桿應力和增大疲勞壽命為原則，并運用零階優化算法對彈性桿進行了結構優化設計。隨后在ANSYS軟件中對其進行了模態和疲勞壽命的分析，仿真結果驗證了彈性桿的引入不會使系統發生共振破壞系統結構，彈性桿的疲勞壽命滿足使用要求，也說明了彈性桿的結構優化設計是正確的。研究結果為在電動負載模擬器中合理使用彈性桿提供了一定的指導作用，以及進一步對彈性桿和電動負載模擬器的結構優化設計奠定了基礎。

［1］韓業紅.舵機電動力矩加載臺控制系統設計與仿真［D］.西安：西北工業大學，2005.

［2］方強.被動式力矩伺服控制系統設計方法及應用研究［D］.哈爾濱：哈爾濱工業大學，2006.

［3］李成功，勒紅濤，焦宗夏.電動負載模擬器多余力矩產生機理及抑制［J］.北京航空航天大學學報，2006，32（2）：205-206.

［4］王鑫，馮冬竹.引入彈簧桿的電動負載模擬器實驗研究［J］.電機與控制學報，2012，16（9）：91-94.

［5］李有堂，于立群.扭轉條件下過渡圓角半徑及徑比對圓周疲勞壽命的影響［J］.蘭州理工大學學報，2008，34（5）：32-35.

［6］符文星，朱蘇朋，孫力.彈性桿剛度對電動負載模擬器的性能影響研究［J］.彈箭與制導學報，2009，29（2）：286-288.

［7］鐘海峰，和欽象，祖磊.基于ANSYS的纖維纏繞復合材料傳動軸的優化［J］.玻璃鋼/復合材料，2015（3）：20-25.

［8］陳然，曹詠弘，孫華東.基于ANSYS的內燃機曲軸的模態分析［J］.煤炭工程，2015，47（4）：108-113.

［9］段紅燕，李有堂，田利.扭轉條件下40Cr的超低周疲勞斷裂研究［J］.材料熱處理技術，2008，37（22）：26-27.

［10］張亞軍.S-N疲勞曲線的數學表達式處理方法探討［J］.理化檢驗-物理分冊，2007，43（11）：563-565.

（編輯：李妮）

Load simulator elastic rod structure optimization and finite element analysis

YANG Ruifeng1，2，LIU Zhikai1，2，GUO Chenxia1，2，ZHANG Peng1，2
（1.School of Instrument and Electronics，North University of China，Taiyuan 030051，China；2.Key Laboratory of Instrumentation Science&Dynamic Measurement，Ministry of Education，North University of China，Taiyuan 030051，China）

For elastic rod used in the electric load simulator，in order to improve its performance，its structure was optimizedand analyzed in finite element method.According to the torsional strength conditions，the minimum diameter electric rod was determined.The length design of the electric rod was optimized with the load gradient of load simulator.To reduce the stress of the electric rod，the zero-order optimization was used for the optimization and optimal solution was obtained.The ANSYS software was used for finite element analysis of the elastic rod modal and fatigue life analysis.Simulation results show that the natural frequency of the elastic rod and fatigue life meet the electric load simulator requirements.The results of elastic rod in the electric load simulator plays a role and has guiding significance in further optimized design.

electric loadsimulator；elastic rod；optimizedstructuraldesign；modal analysis；fatigue life analysis

A

1674-5124（2016）05-0119-05

10.11857/j.issn.1674-5124.2016.05.025

2015-12-21；

2016-02-01

國家自然科學基金項目（51375462）國家國際科技合作項目（2014DFR70650）高等學校博士學科點專項科研項目（20121420110003）

楊瑞峰（1969-），男，山西忻州市人，教授，博士生導師，研究方向為自動化測試與控制技術。