ERV族分布下帶投資的雙險種風險模型的破產概率

王施施, 王文勝, 駱明旭

(杭州師范大學理學院,浙江 杭州 310036)

?

ERV族分布下帶投資的雙險種風險模型的破產概率

王施施, 王文勝, 駱明旭

(杭州師范大學理學院,浙江 杭州 310036)

破產概率；雙險種風險模型；漸近關系式；風險投資策略

1　引言和模型

在實際生活中,保險公司業務種類日益增多,在索賠方面要考慮的因素也越來越復雜,因此經典風險模型中單一險種的情形已不能滿足實際需要.為了更好地描述這些不確定因素,本文引入了帶投資的雙險種風險模型,利用此模型對破產概率進行深入研究.

我們假定保險公司拿出一部分盈余投資Black-Scholes型資本市場指數,且假設該指數的價格過程由幾何布朗運動來表示,那么公司的盈余過程{Ui(t),t≥0}可表示為:

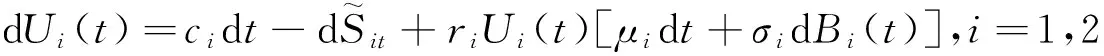
(1)

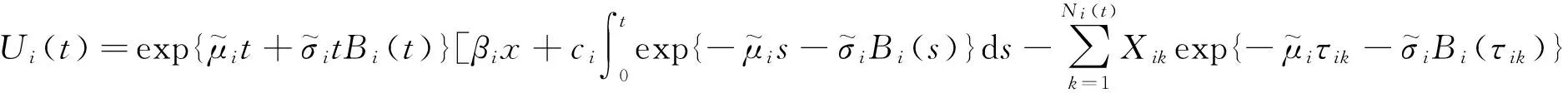
(2)

其中{Ni(t),t≥0,i=1,2}是第i險種到時刻t為止保單發生索賠次數.假設它服從參數為λit的泊松分布,且{N1(t),t≥0},{N2(t),t≥0}相互獨立,而且{Xik,k=1,2,…,i=1,2},{Bi(t),i=1,2,t≥0},{Ni(t),i=1,2,t≥0}都是相互獨立的.

在有限時間T(T>0),關于雙險種情形的破產時刻及破產概率有多種定義.本文主要研究其中的3種,它們具體定義為:

1)定義破產時刻Tmax(x)為:

Tmax(x)=inf{t≥0:max{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相應的破產概率為:

Ψmax(x,T)=P(Tmax(x)≤T)

(3)

2)定義破產時刻Tmin(x)為:

Tmin(x)=inf{t≥0:min{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相應的破產概率為:

Ψmin(x,T)=P(Tmin(x)≤T)

(4)

3)定義破產時刻Tsum(x)為:

Tsum(x)=inf{t≥0:U1(t)+U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相應的破產概率為:

Ψsum(x,T)=P(Tsum(x)≤T)

(5)

在保險精算的應用中破產概率的研究一直是熱門的話題.迄今,國內外很多學者研究過連續或者離散時間風險模型的破產概率.例如,Asmussen和H?jgaard[1],Cossette[2],Chen[3]等.然而,這些都是對單一情形的研究,難免和實際不相符合.后來,二維風險模型逐漸被廣大學者探討和研究出來,如Avram[4],Li[5],Dang[6],Zhang和Wang[7].

本文主要集中研究帶投資的雙險種風險模型的破產概率,給出了破產概率主要結果和其他一些概率以及相應的證明以及證明所需要的引理.

2　定義和主要結果

2.1相關概念

定義1對任意固定的實數α>0,如果分布F滿足

(6)

則稱F屬于R-α族.通常,R族是指所有R-α族關于α在其取值范圍上的并集.

定義2對任意固定的實數0<α≤β<∞,如果分布F滿足

(7)

則稱F屬于ERV-α,-β族.通常,ERV族指所有ERV{-α,-β}族關于α≤β在其取值范圍上的并集.

對于更新風險模型(2),全文假設索賠額分布Fi∈ERV(-α,-β),1<α≤β<∞,且

(8)

假設該條件保證了公司盈余的隨機波動能被趨勢控制,否則公司將以概率1破產.詳見文獻[8-9].

從現在開始除非特別指明,所有極限過程均指x→∞時情況,對于兩個正函數f(·)和g(·),如果limf(x)/g(x)=1，記為f(x)～g(x);如果liminff(x)/g(x)≥1,記為f(x)g(x);如果limsupf(x)/g(x)≤1,記為f(x)g(x);如果limsupf(x)/g(x)<∞,記為f(x)=○(g(x)).

2.2主要結果

定理1考慮更新風險模型(2),令LN(yi;a,b2)表示參數為a和b2的對數正態分布,如果索賠額{Xik,k=1,2,…,i=1,2}是獨立同分布且非負的隨機變量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.則式(3)定義的破產概率具有如下漸近關系式:

(9)

定理2考慮更新風險模型(2),令LN(yi;a,b2)表示參數為a和b2的對數正態分布,如果索賠額{Xik,k=1,2,…,i=1,2}是獨立同分布且非負的隨機變量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.則式(4)定義的破產概率具有如下漸近關系式:

(10)

定理3考慮更新風險模型(2),令LN(yi;a,b2)表示參數為a和b2的對數正態分布,如果索賠額{Xik,k=1,2,…,i=1,2}是獨立同分布且非負的隨機變量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.則式(5)定義的破產概率具有如下漸近關系式:

(11)

3　定理的證明

3.1引理

引理1考慮單一險種情形下,具有共同分布F的獨立索賠額序列{Xk,k=1,2,…},如果F∈ERV(-α,-β),1<α≤β<∞,則

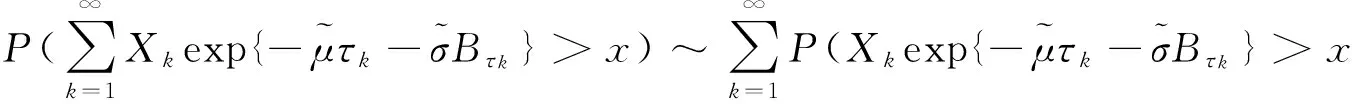
(12)

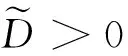
引理2設X和Y是兩個相互獨立的非負隨機變量,X的分布F∈ERV(-α,-β),1<α≤β<∞,且存在0<δ<α,使得EYβ+δ<∞,則存在常數D>0,使得

(13)

證明參見文獻[11]中定理3.5.

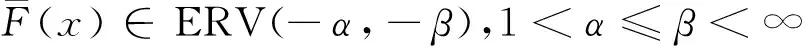
(14)

證明參見文獻[11].

(15)

證明參見文獻[12]中引理3.1.

引理5對于單一險種情形下帶投資的風險模型,

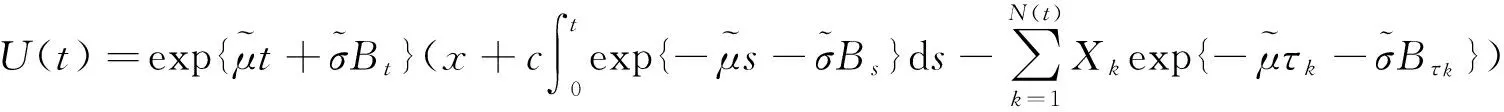
其中LN(y;a,b2)表示參數為a和b2的對數正態分布,如果索賠額分布F∈ERV(-α,-β),1<α≤β<∞,且式(8)成立,則

(16)

證明在假設條件(8)下,由引理1式(12)得

引理6對于單一險種情形下帶投資的風險模型,

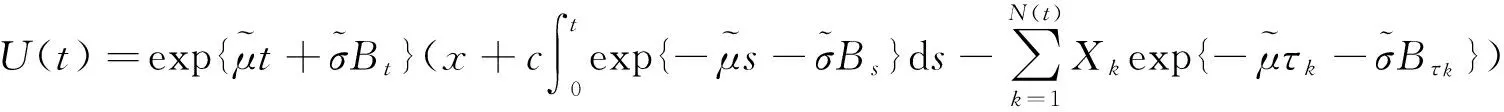
其中LN(y;a,b2)表示參數為a和b2的對數正態分布,如果索賠額分布F∈ERV(-α,-β),1<α≤β<∞,且式(8)成立,則

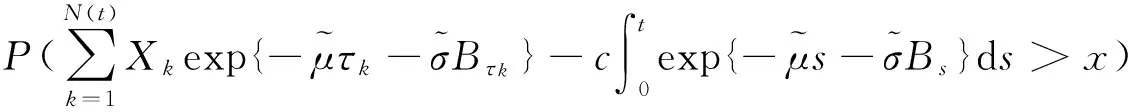
(17)

證明對?ε>0,

I1(x)-I2(x).

(18)

(19)

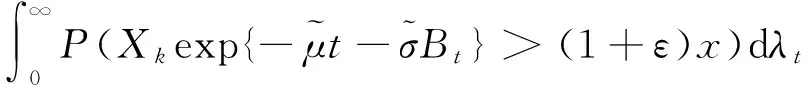
(20)

選取適當的ρ>0,使得β′(1-ρ)>β.根據定義2式(7)有

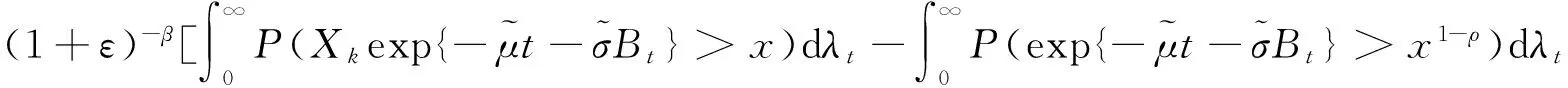
(21)

根據引理2,存在0<δ<α,和常數D>0,使得

(22)

易證式(22)中的積分是有限常數.對于前面定義的β′,有β′(1-ρ)>β,在式(8)條件下,有

(23)

由式(22)、(23)和引理4的式(15)得

綜上所述

(24)

進一步,由式(19)(22)和引理4的式(15)得

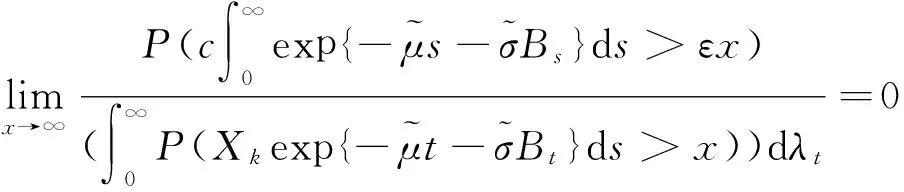
(25)

所以由式(18)(24)(25)和ε>0的任意性得

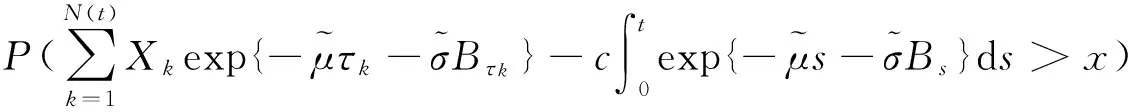
3.2定理1的證明

首先證明式(3)定義破產概率的上界,由破產概率Ψmax(x,T)的定義及條件{N1(t),t≥0},{N2(t),t≥0}相互獨立,以及{Xik,k=1,2,…},(i=1,2)獨立可知

Ψmax(x,T)=P(Tmax(x)≤T)=P(Ui(t)<0,i=1,2,?0≤t≤T)=

由引理5得

Ψmax(x,T)

(26)

接著要證明破產概率的下界,根據其獨立性有

Ψmax(x,T)=P(Ui(t)<0,i=1,2,?0≤t≤T)=

由引理6得

Ψmax(x,T)

(27)

所以結合式(26)和(27)可知

3.3定理2的證明

根據破產概率Ψmin(x,T)的定義及在定理2條件下,令s(xi)=inf{t≥0,Ui(t)<0},則

3.4定理3的證明

和定理1的證明一樣,首先考慮式(5)定義破產概率的上界,由定理3的條件得

由引理3得

所以

(28)

下面考慮破產概率的下界.

由式(5)破產概率定義得

由引理3得

所以

Ψsum(x,T).

(29)

由式(28)和式(29)得

[1] ASMUSSEN S, H?JGAARD B. Approximations for finite horizon ruin probabilities in the renewal model[J]. Scand Actuar J,1999(2):106-119.

[2] COSSETTE H, LANDRIAULT D, MARCEAU E. Ruin probabilities in the discrete time renewal risk model[J]. Insurance Math Econom,2006,38(2):309-323.

[3] CHEN Y, NG K W. The ruin probabilities of the renewal model with constant intrest force and negatively dependent heavy-tailed claims[J]. Insurance Math Econom,2007,40(3):415-423.

[4] AVRAM F, PALMOWSKI Z, PISTORIVS M. A two-dimensional ruin problem on the positive quardrant[J]. Insurance:Mathematics and Economics,2008,42(1):227-234.

[5] LI J H, LIU Z M, TANG Q H. On the ruin probabilities of a bidimensional perturbed risk model[J]. Insurance:Mathematics and Economics,2007,41(1):185-195.

[6] DANG L F, ZHU N, ZHANG H M. Survival probability for a two-dimensional risk model[J]. Insurance:Mathematics and Economics,2009,44(3):491-496.

[7] ZHANG Y Y, WANG W S. Ruin probabilities of a bidimensional risk model with investment[J]. Statist Probab Lett,2012,82(1):130-138.

[8] FROLOVA A, KABANOV Y, PERGAMENSHCHIKOV S. In the insurance business risky investments are dangerous[J]. Finance Stoch,2002,6(2):227-235.

[9] DUFRESNE D. The distribution of a perpetuity, with applications to risk theory and pension funding[J]. Scnd Actuar J,1990(1):39-79.

[10] TANG Q, TSITSIASHVILI G. Finite-and infinite-time ruin probability in the presence of stochastic returns on investments[J]. Adv Appl Probab,2004,36(4):1278-1299.

[11] EMBRECHTS PAUL, KlüPPELBERG C, MIKOSCH T. Modelling extremal events[J]. Applications of Mathematics,2010,71(2):183-199.

[12] TANG Q, SU C, JIANG T, et al. Large deviations for heavy-tailed random sums in compound renewal model[J]. Statist Probab Lett,2001,52(1):91-100.

[13] GJESSING H K, PAULSEN J. Present value distributions with applications to ruin theory and stochastic equations[J]. Stochastic Process Appl,1997,71(1):123-144.

[14] CLINE D B H, SAMORODNITSKY G. Subexponentiality of the product of independent random variables[J]. Stochastic Process Appl,1994,49(1):75-98.

[15] WANG K Y, WANG Y B, GAO Q W. Uniform asymptotics for the finite-time ruin probability of a dependent risk model with a constant interest rate[J]. Methodol Comput Appl Probab,2013,15(1):109-124.

[16] YANG Y, LEIPUS R, SIAULYS J, et al. Uniform estimates for the finite-time ruin probability in the dependent renewal risk model[J]. J Math Anal Appl,2011,383(1):215-225.

[17] SHEN X M, ZHANG Y. Ruin probabilities of a two-dimensional risk model with dependent risks of heavy tail[J]. Statistics and Probability Letters,2013,83(7):1787-1799.

[18] WEI L. Ruin probability of the renewal model with risky investment and large claims[J]. Sci China SerA,2009,52(7):1539-1545.

Ruin Probability of Two-type-risk Insurance Risk Model under ERV Distribution

WANG Shishi, WANG Wensheng, LUO Mingxu

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

ruin probability; risk model for two-type-risk insurance; asymptotic relationship; venture capital strategy

2015-09-29

王文勝(1972—),男,教授,主要從事隨機過程,金融數學研究.E-mail:wswang@aliyun.com

10.3969/j.issn.1674-232X.2016.05.015

O211.9MSC2010:62P20

A

1674-232X(2016)05-0533-09