一種改進的基于BDS三頻非差觀測的周跳實時探測與修復模型

高　杰,謝建濤

(1.信息工程大學 地理空間信息學院，河南 鄭州 450001；2. 西安測繪總站，陜西 西安 710054；3.信息工程大學 導航與空天目標工程學院，河南 鄭州 450001)

?

一種改進的基于BDS三頻非差觀測的周跳實時探測與修復模型

高杰1,2,謝建濤3

(1.信息工程大學 地理空間信息學院，河南 鄭州 450001；2. 西安測繪總站，陜西 西安 710054；3.信息工程大學 導航與空天目標工程學院，河南 鄭州 450001)

BDS三頻觀測條件下可以組合得到具有優良特性的虛擬載波觀測量，有利于改善非差觀測數據的周跳實時探測與修復。文中提出一種基于BDS三頻非差數據的周跳實時探測與修復模型:首先，采用消電離層無幾何HMW組合觀測量探測和修復EWL周跳;然后，將經過修復的EWL觀測量與WL組合消除幾何相關項，忽略電離層延遲殘差進而確定WL周跳;最后采用經過修復的WL觀測量與NL組合形成無幾何觀測量，并通過優化載波相位組合確定電離層延遲的變化量以探測和計算NL周跳，并通過簡單變換得到原始載波觀測量的周跳值。通過實測BDS三頻數據對模型可行性進行驗證分析，結果表明，即使在30 s的采樣率以及電離層活動活躍條件下，該模型都可有效實時探測和修復各類周跳。

BDS；三頻；周跳；電離層延遲；優化載波相位組合

基于載波相位觀測量的實時精密定位手段以其高精度的特點而在各個領域得到發展和應用。然而，載波相位觀測量由于導航信號遮擋、惡劣的電離層條件以及多路徑等造成累積相位產生一個整周數的跳變，因此，必須在數據預處理過程中對周跳進行實時探測與修復，以保證模糊度解算的可靠性和正確性。

目前載波相位精密導航定位中的周跳探測方法主要有碼相組合法、電離層殘差法、多普勒積分法以及歷元間差分法[1-2]。北斗導航衛星系統在體制上的最大優勢在于率先實現三頻數據的播發。相比雙頻數據，三頻數據能夠形成更多更優的線性組合，其等效波長更長，觀測噪聲和電離層影響也更小，這些優良組合為周跳探測、修復可提供更多選擇和幫助。

文獻[1]提出一種實時的算法，用以探測和修復三頻GNSS數據中的周跳值，并將該算法應用于單點定位數據處理中。文獻[2]提出的算法中應用兩個幾何無關線性組合以及LAMBDA算法對周跳備選值進行搜索，并結合GPS三頻實測數據進行周跳的探測與修復，但是隨著數據采樣間隔的增大會造成電離層延遲變化量增大，該模型的效率明顯降低。文獻[3]通過北斗三頻載波相位無幾何組合探測和修復周跳，修復方法較為復雜。文獻[4]將載波觀測量和偽距觀測量進行組合，但探測效果受偽距噪聲的影響，且這兩種方法都未能充分考慮不同的歷元間電離層延遲變化水平。文獻[5]基于GNSS三頻數據構造5個消電離層消幾何觀測量，分三步實時探測和修復周跳，該算法的前提是電離層延遲變化隨時間平滑變化，在電離層活躍條件下應用有限。本文提出一種基于BDS三頻非差數據的周跳實時探測與修復模型，充分考慮電離層延遲變化造成的影響，依次對EWL，WL和NL虛擬觀測量進行周跳實時探測與修復，計算得到原始載波相位觀測量的周跳值，并通過實測BDS三頻數據對模型可行性進行驗證分析。

1　TCAR觀測量

1.1觀測量線性組合

基于三頻數據的非差觀測量可描述為[4]

(1)

(2)

式中：組合系數i,j,k為整數；P,φ表示以“米”為單位的非差偽距和載波相位觀測量。組合之后的虛擬載波頻率定義為

(3)

對于BDS，3個頻點為f1=1 561.098 MHz，f2=1 207.140 MHz，f3=1 268.520 MHz。

組合觀測量的一階電離層延遲尺度因子(ISF)β(i,j,k)和載波噪聲因子(PNF)μ(i,j,k)分別表示為式(4)和式(5)。

(4)

(5)

1.2最優EWL,WL和NL組合觀測量

近些年來，國內外的許多學者都對適用于模糊度解算的三頻載波觀測最優線性組合進行了研究，得出許多具有長波長、弱電離層延遲、低噪聲的最優虛擬觀測量。對于BDS系統，三頻最優組合觀測值的相關特性如表1所示。

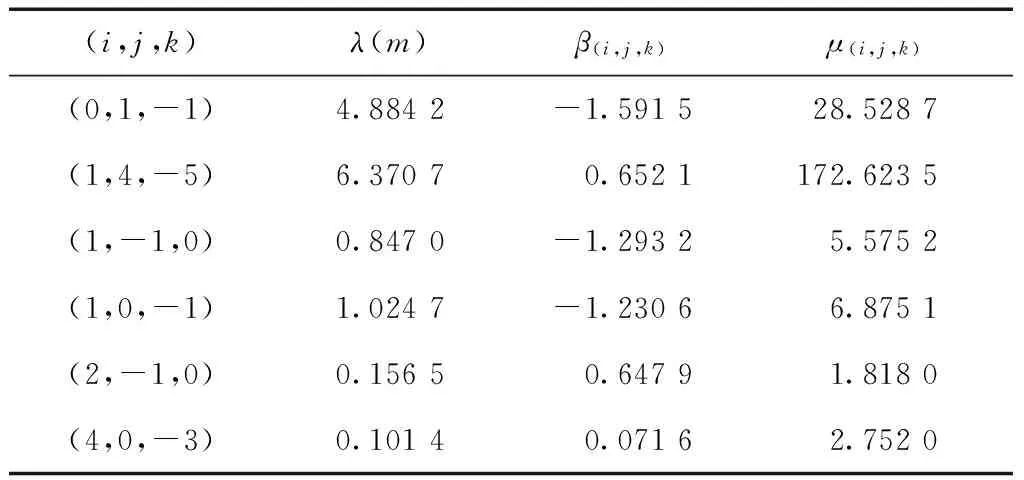
表1　不同載波線性組合觀測量的特性

本文在綜合考慮虛擬波長、電離層延遲因子以及虛擬觀測噪聲的基礎上，選取EWLφ(0,1,-1)、WLφ(1,0,-1)和NLφ(2,-1,0)3個虛擬觀測量進行周跳實時探測和修復。

2　周跳實時探測與修復算法優化

2.1EWL周跳探測與修復

EWL虛擬觀測量上的周跳值通過HMW線性組合觀測量進行解算。HMW組合觀測量保留了EWL模糊度參數，且不受幾何相關項以及對流層延遲誤差和電離層延遲誤差的影響，其數學表現形式為

(6)

對相鄰的兩個歷元作差，得到周跳的表達式為

(7)

當|ΔN(0,1,-1)|>0.5時，認為發生周跳，周跳值算式為

(8)

(9)

2.2WL周跳探測與修復

當EWL組合觀測量的周跳進行修正后，可與WL組合觀測量形成無幾何觀測量。

(10)

式中，η1=β(0,1,-1)-β(1,0,-1)=0.298，相鄰歷元間作差得到周跳表達式為

(11)

對于30 s的采樣率，式(11)中的電離層延遲項η1ΔI是小項，與λ(1,0,-1)相比可以忽略其影響。與EWL相同，當|ΔN(1,0,-1)|>0.5時，認為WL發生周跳，周跳值算式為

(12)

依據誤差傳播定律，ΔN(1,0,-1)的標準差σΔN(1,0,-1)≈0.146周，對于30 s采樣率，電離層延遲變化量平緩變化，假定ΔI=0.1 m，η1ΔI為0.03周。因此，可以假設ΔN(1,0,-1)服從均值為0.03周、標準差為0.146周的正態分布[5]。因此，WL周跳探測和修復的成功率為

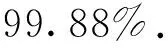
(13)

2.3NL周跳探測與修復

與上面相似，將周跳值得到確定的WL組合觀測量應用到NL觀測量周跳探測與修復中，以消除NL觀測量的幾何相關項，如式(14)所示。

(14)

式中，η2=β(1,0,-1)-β(2,-1,0)=1.941，相鄰歷元間作差得到NL周跳表達式為

(15)

式中,η2=1.941，電離層延遲誤差被放大，而NL波長更短，λ(2,-1,0)=0.156 5m，因此，低采樣率和電離層活躍條件、電離層延遲的影響不能被忽略，可通過式(16)計算得到。

(16)

式中，k1i=(f1/fi)2，i=2，3。對于每一個歷元，當原始載波觀測量上的周跳得到準確的修復之后，ΔI都可計算得到。

當EWLφ(0,1,-1)，WLφ(1,0,-1)上的周跳得到確定之后，另一個WL觀測量WLφ(1,-1,0)上的周跳值可由式(17)計算得到。

(17)

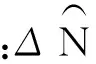
當|ΔN(2,-1,0)|>0.5時，認為NL發生周跳，周跳值算式為

(18)

依據誤差傳播定律，ΔN(2,-1,0)的標準差σΔN(2,-1,0)≈0.187周，當η2ΔI得到準確計算之后，可以假設ΔN(2,-1,0)服從均值為零、標準差為0.187周的正態分布[5]。因此，NL周跳探測和修復的成功率為

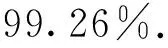
(19)

當EWL，WL和NL周跳得到修復之后，原始載波觀測量上的周跳值可由式(20)計算得到。

(20)

(21)

2.4特殊周跳組合

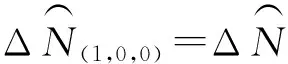
(22)

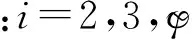
(23)

式中i=2,3。

(24)

(25)

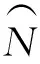
(26)

設定原始載波相位的非差觀測噪聲為σφ=0.2 cm，將σΔI分別設為0.5 cm和1 cm，得到的優化系數如表2所示。

當|ΔYi|>n·σΔYi時，認為發生周跳，這里僅僅是對周跳進行判斷，為了避免“漏探”情況的發生，采用嚴格的3σΔYi。σΔI=1 cm時，對于一周的跳變，|a·ΔN1·λ1+b·ΔNi·λi|≈10 cm，3σΔYi≈4 cm，因此當ΔI<6 cm時，即使一周的周跳跳變量，也可進行有效的探測，而ΔI>6 cm屬于電離層活動非常劇烈的情況，是比較罕見的，而且，即使出現“誤探”的情況，依然可以采用上一歷元的ΔI，對NL組合觀測量的周跳進行有效的探測與修復。

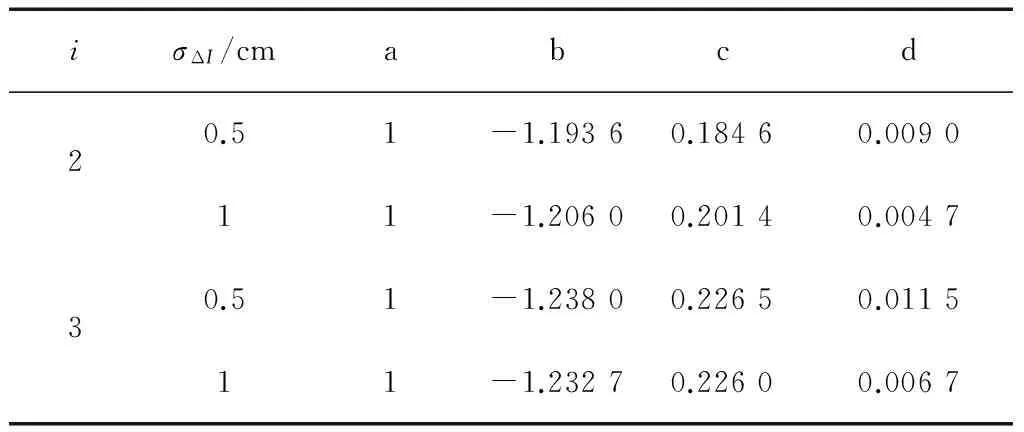
表2　最優組合系數

3　實驗分析

為了驗證本文模型的有效性和可靠性，這里采用一組正常多路徑水平下，經過周跳修復的“干凈”BDS三頻實測數據進行實驗分析，選取3號衛星和9號衛星，3號衛星時長為1 d，9號衛星為地方時10：40-22：40，采樣率均為30 s。其電離層延遲變化量ΔI的時間序列分別如圖1和圖2所示。

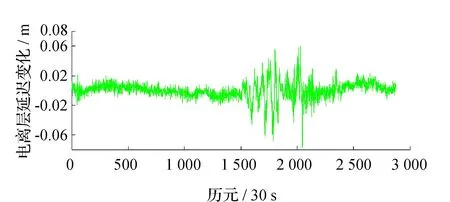
圖1　電離層延遲變化(C03)

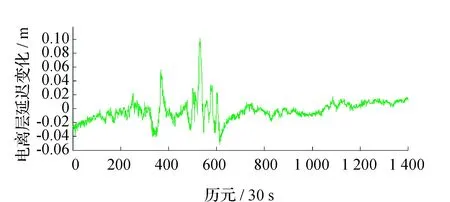
圖2　電離層延遲變化(C09)

圖1在1500個歷元以后以及圖2在380個歷元之后都出現較大幅度的波動，這是由當地時間下午時分電離層活動劇烈造成的。對電離層延遲變化量ΔI進行數理統計得到其中誤差σΔI=1 cm，最小值為-7.8 cm，最大值為6.0 cm。無周跳狀態下，EWL,WL和NL周跳浮點解ΔN(0,1,-1)，ΔN(1,0,-1)和ΔN(2,-1,0)的時間序列值如圖3～圖8所示。

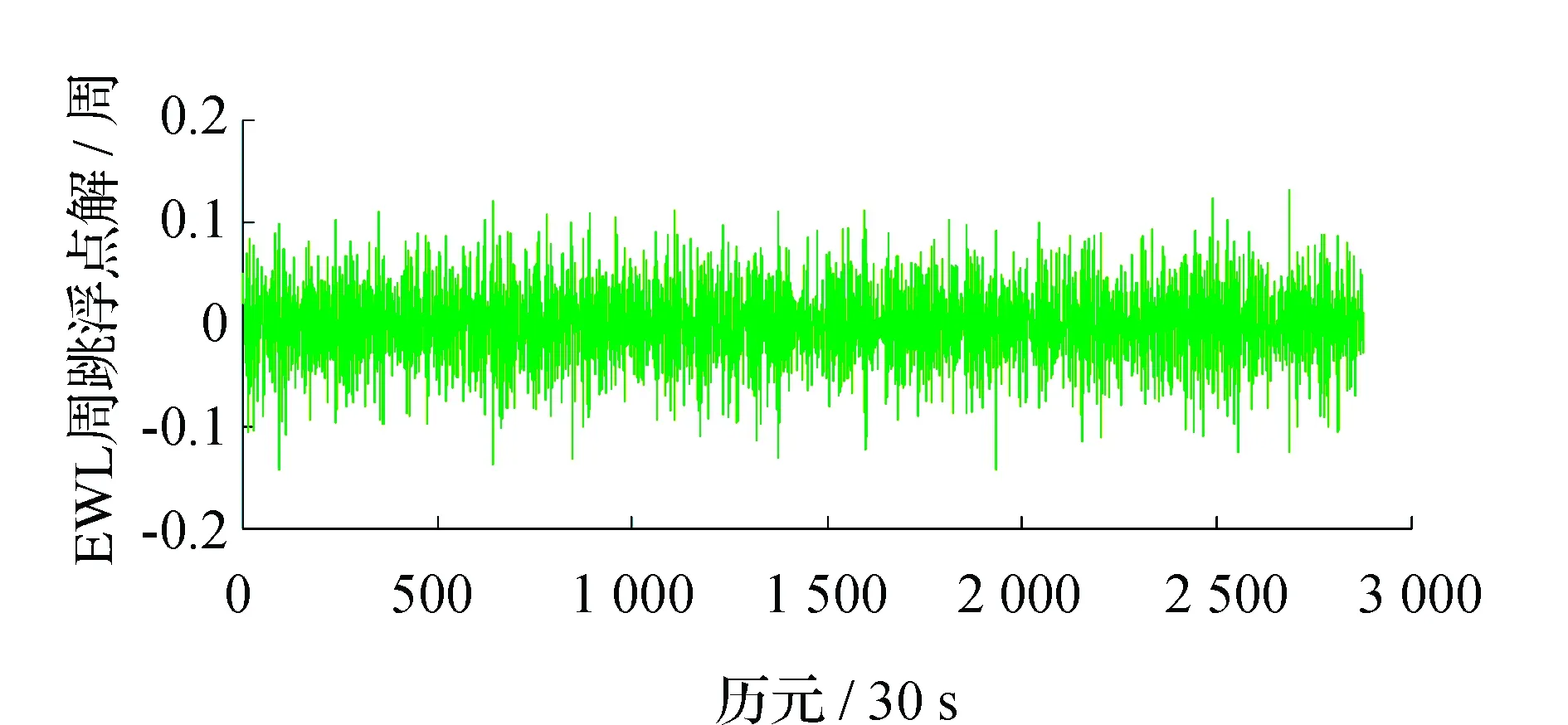
圖3　ΔN(0,1,-1)隨機噪聲(C03)

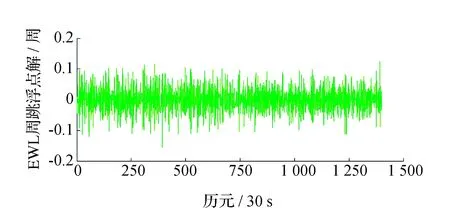
圖　4ΔN(0,1,-1)隨機噪聲(C09)

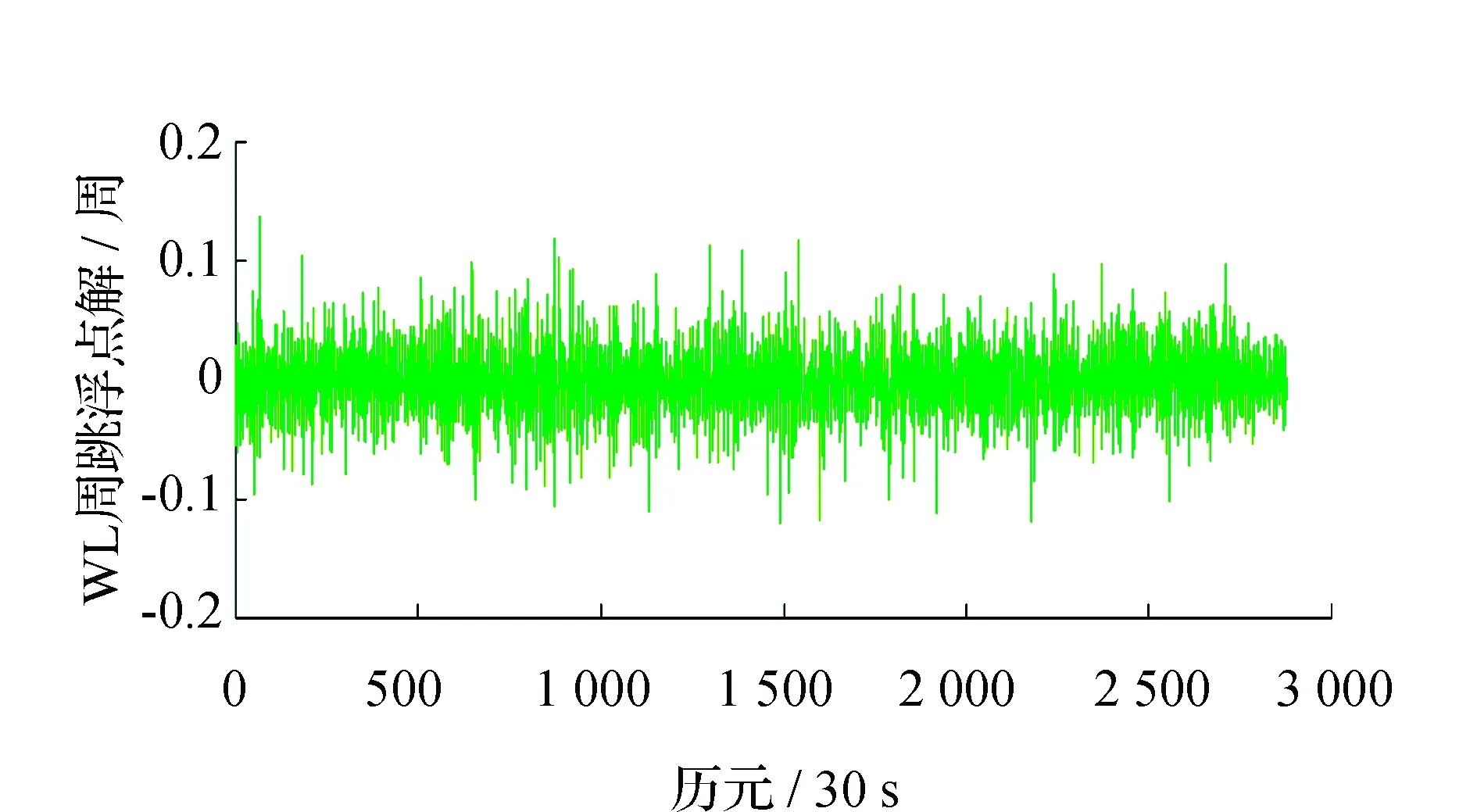
圖5　ΔN(1,0,-1)隨機噪聲(C03)

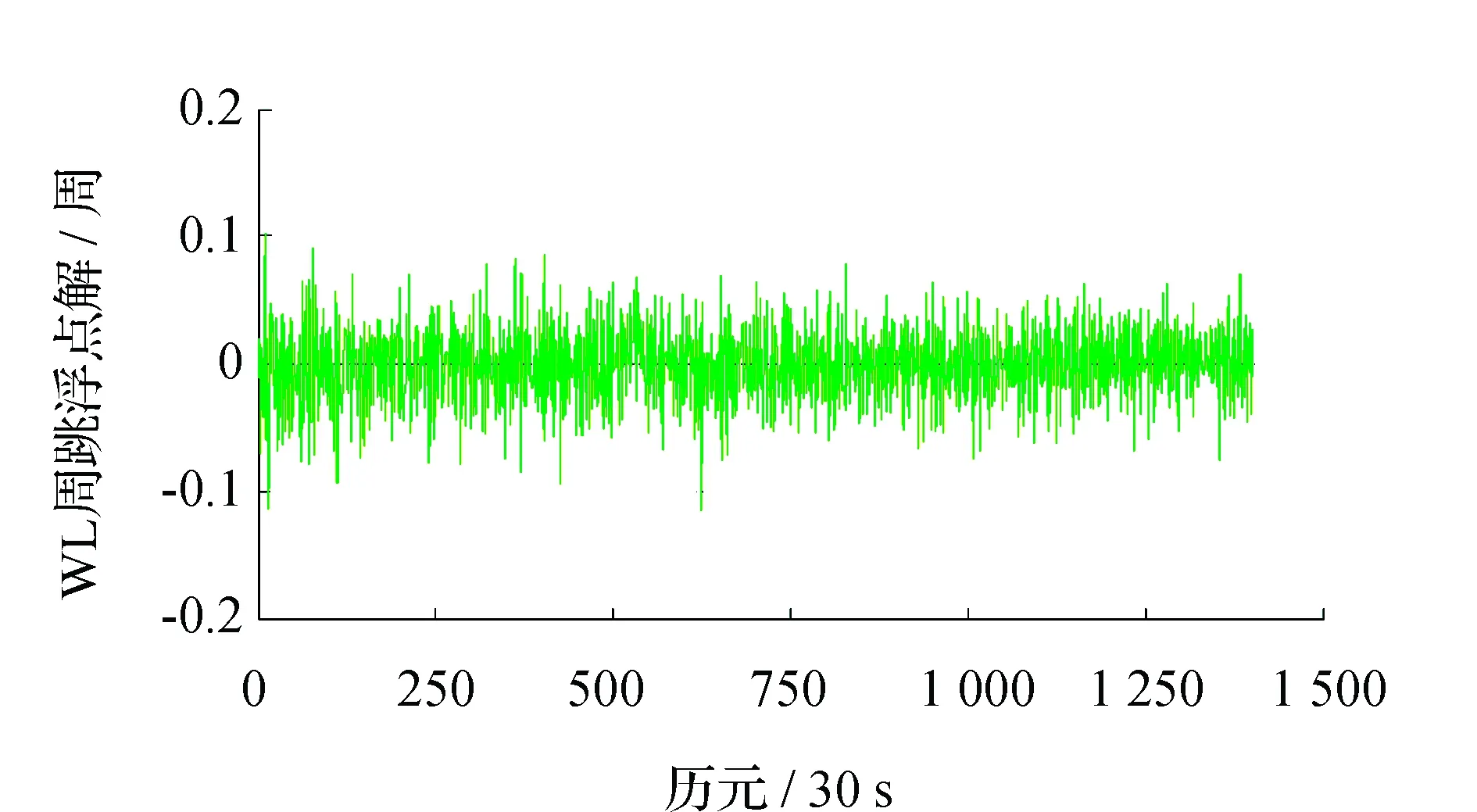
圖6　ΔN(1,0,-1)隨機噪聲(C09)

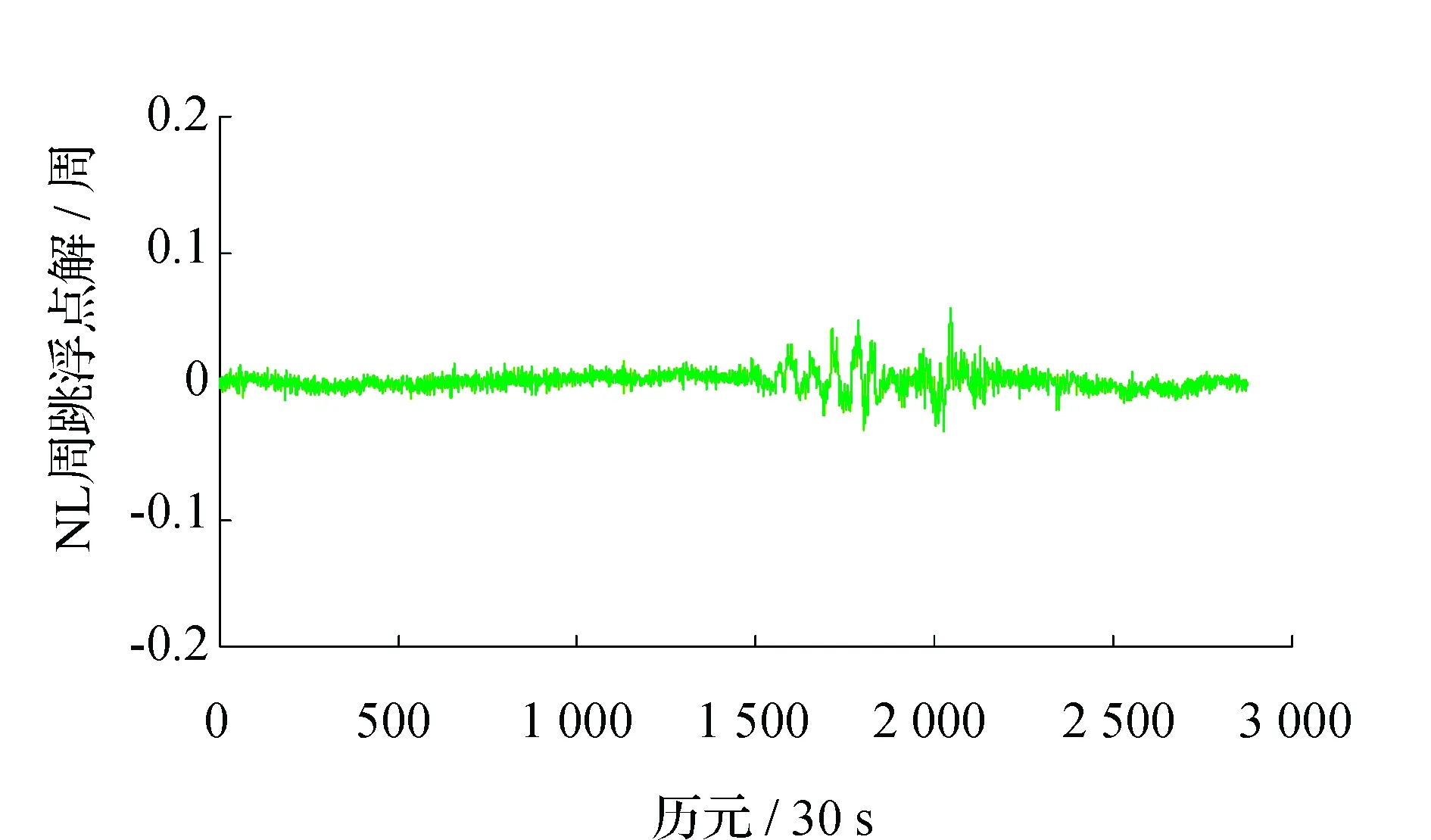
圖7　ΔN(2,-1,0)隨機噪聲(C03)

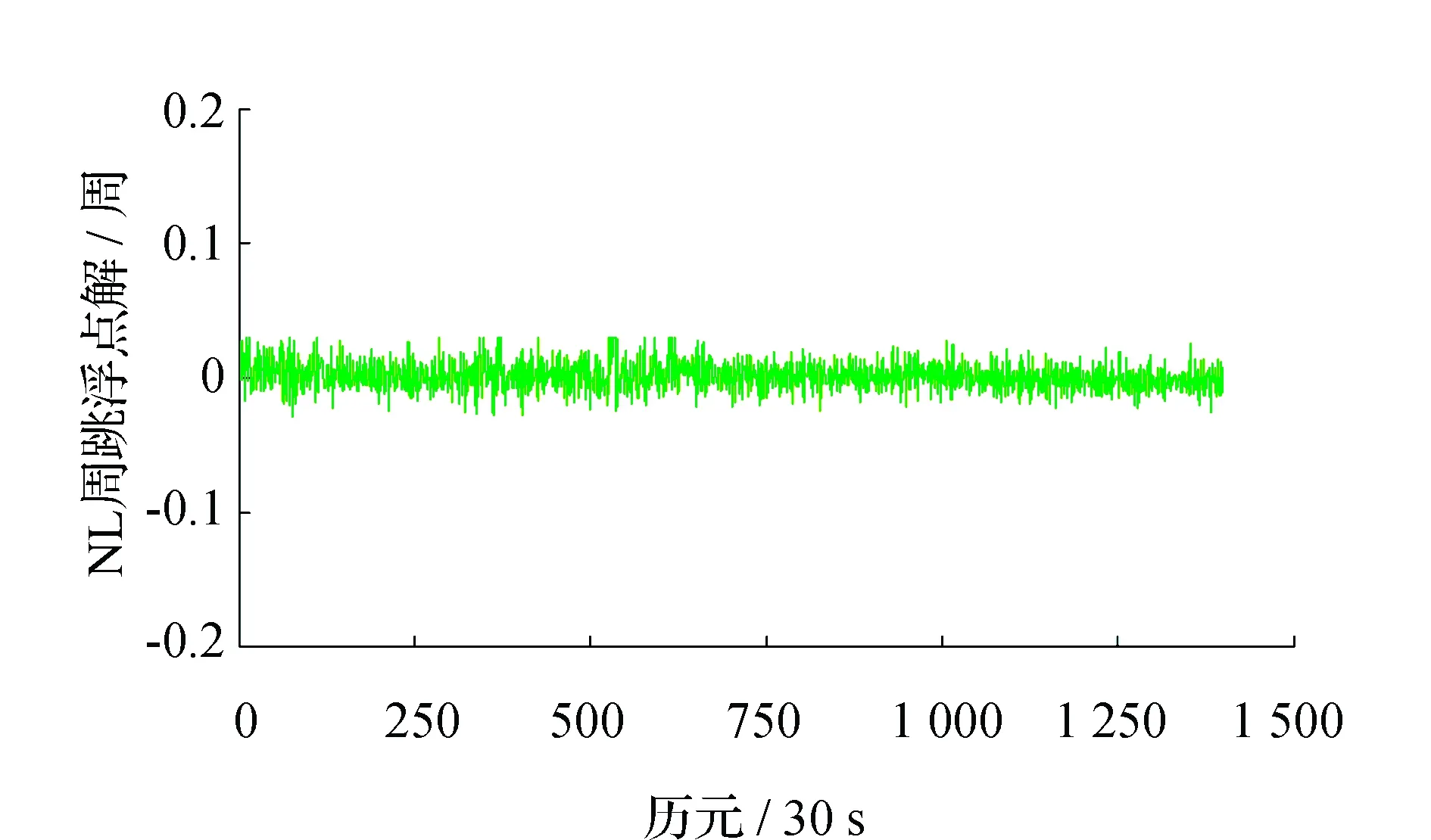
圖8　ΔN(2,-1,0)隨機噪聲(C09)

由圖3～圖6可以看出，ΔN(0,1,-1)和ΔN(1,0,-1)的隨機觀測噪聲都比較小，基本保持在0.1周之內，圖7和圖8中，ΔN(2,-1,0)的隨機觀測噪聲更小,這都有利于周跳的準確探測和修復。為了驗證本文模型周跳實時探測和修復的可靠性，采用電離層較為平穩的0～800 歷元(C03)、100～300 歷元(C09)和電離層活躍的1 600～2 000歷元(C03)、300～600歷元(C09)的觀測數據進行實驗，分別記為時段1、時段2、時段3和時段4。將周跳類型設置為3種：大周跳、小周跳和特殊周跳，對結果進行總結分析，如表3、表4所示。

由表3、表4可以看出，對于衛星C03，第3時段為電離層活躍時段，在1 788歷元，即使電離層延遲變化量達到6 cm，對應的周跳也能夠探測和修復成功。對于衛星C09，第4時段為電離層活躍時段，在535歷元，電離層延遲變化量為7 cm，對應的周跳能夠探測和修復成功。

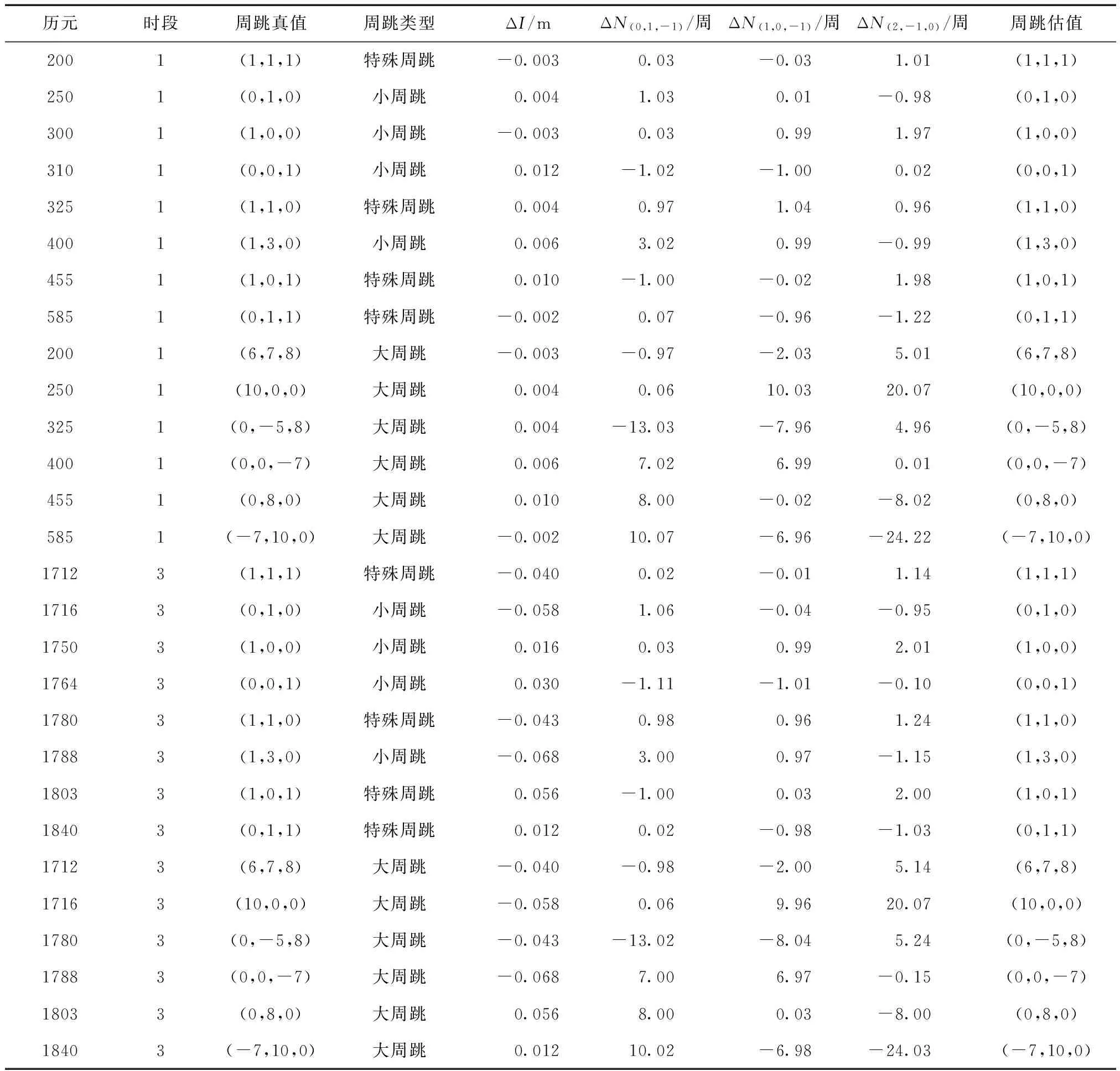
表3　周跳探測與修復結果(C03)

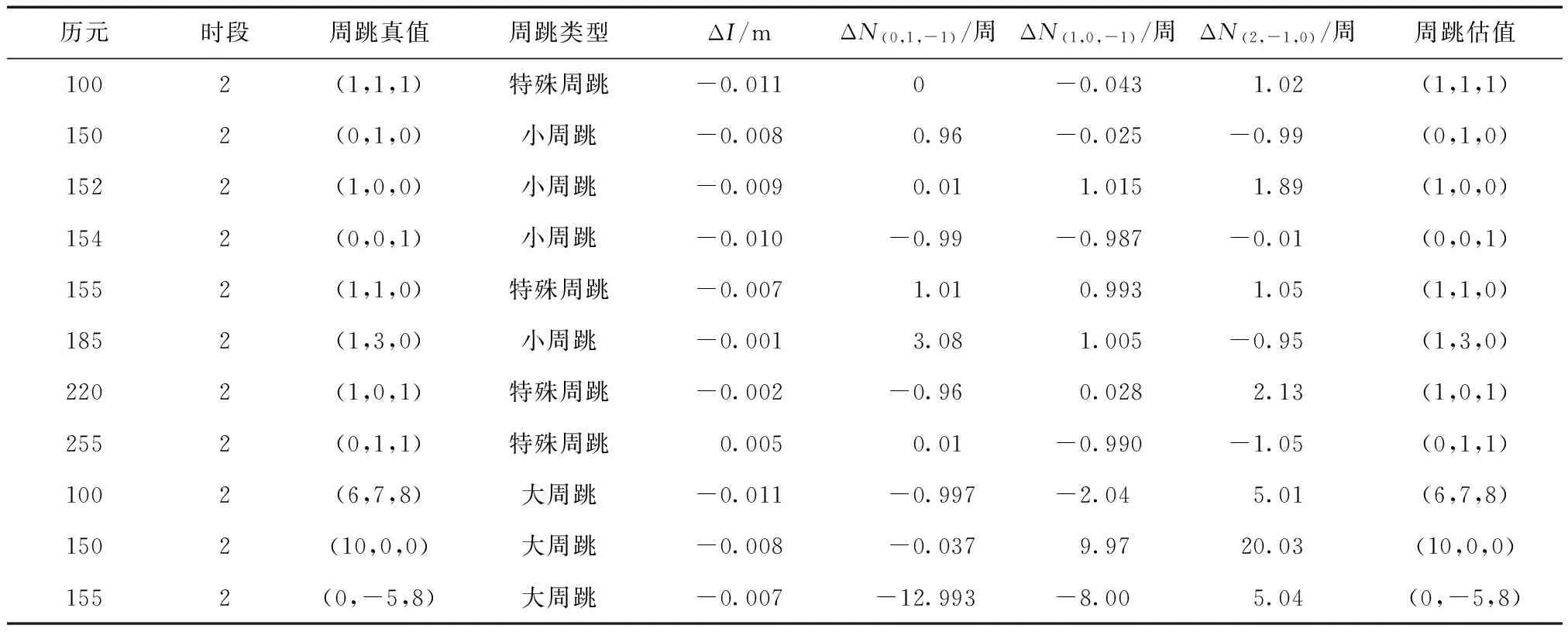
表4　周跳探測與修復結果(C09)

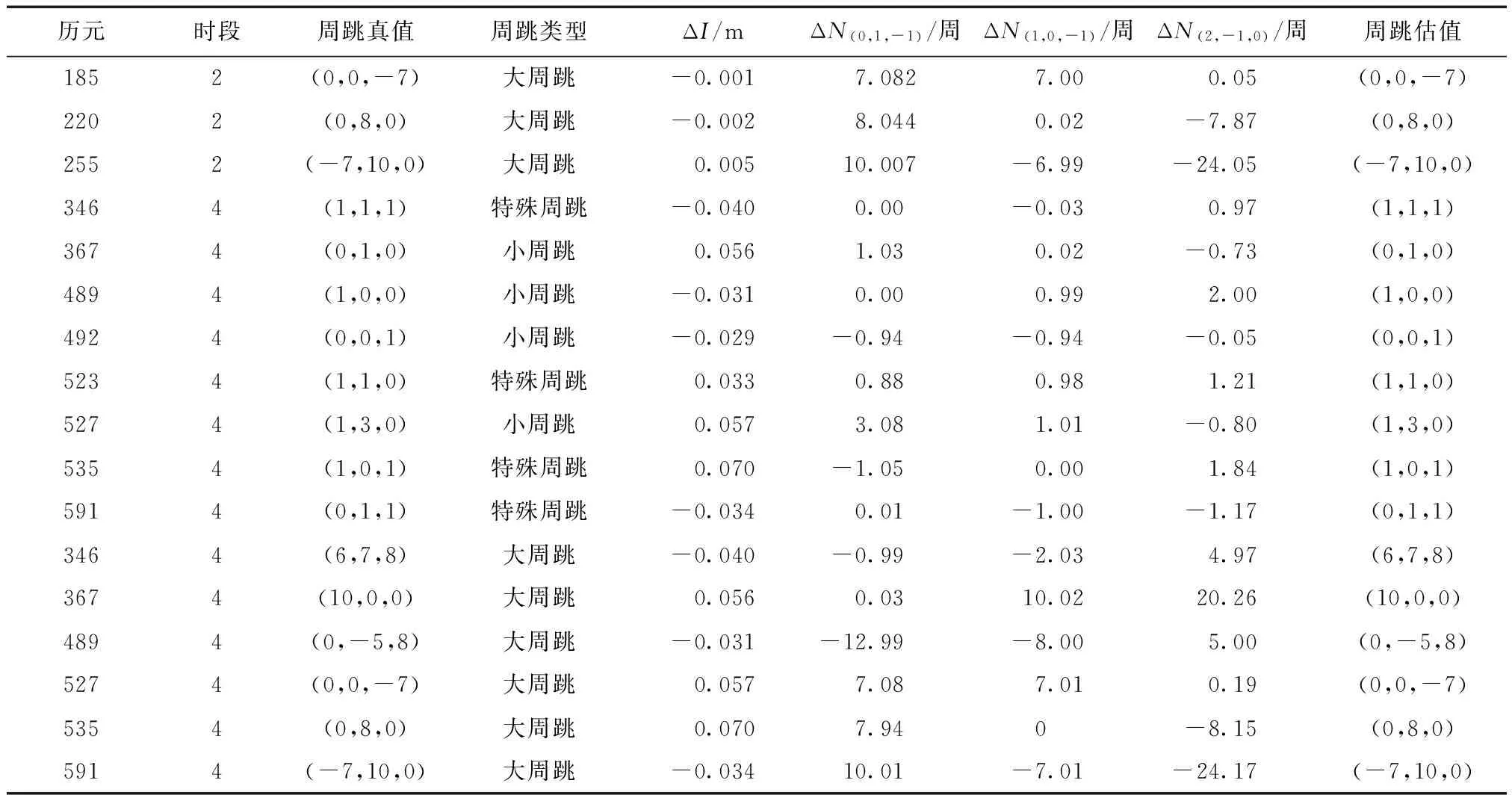
續表4

4　結　論

BDS三頻觀測條件下可以組合得到具有優良特性的虛擬載波觀測量，有利于改善非差觀測數據的周跳實時探測與修復，本文提出一種基于BDS三頻非差數據的周跳實時探測與修復模型，充分考慮電離層延遲變化對周跳實時探測與修復過程中造成的影響，通過優化載波相位組合確定電離層延遲的變化量，以提高NL周跳的探測與修復的成功率和可靠性。最后，通過實測BDS三頻數據對模型可行性進行驗證，結果表明，即使在30s的采樣率以及電離層活動活躍條件下，該模型都能有效的實時探測和修復各類周跳，可應用于北斗三頻非差數據周跳實時探測和修復。

[1]ZHEN D,STEFAN K, OTMAR L.Realtime cycle slip detection and determination for multiple frequency GNSS[J].Proceedings of the 5th workshop on positioning, navigation and communication,2008.

[2]DAI Z, KNEDLIK S, LOFFELD O.Instantaneous triple-frequency GPS cycle-slip detection and repair[J]. Int J Navig Obs,2009.

[3]黃令勇,宋力杰,王琰,等.北斗三頻無幾何相位組合周跳探測與修復[J].測繪學報,2012,41(5):763-768.

[4]李金龍,楊元喜,徐君毅,等.基于偽距相位組合實時探測與修復GNSS三頻非差觀測數據周跳[J].測繪學報,2011 ,40(6):717-722.

[5]de LACY M C, REGUZZONI M,SANSO F.Real-time cycle slip detection in triple-frequency GNSS[J].GPS Solut,2012,16:353-362.

[6]申俊飛,何海波,郭海榮，等．三頻觀測量線性組合在北斗導航中的應用[J].全球定位系統,2012,37(6): 37-40.

[7]柯福陽,王慶,潘樹國.GPS/GLONASS周跳探測[J].測繪科學技術學報,2013,30(20):114-118.

[8]程鵬飛,李瑋,秘金鐘.北斗導航衛星系統測距信號的精度分析[J].測繪學報,2012，41(5)：690-695.

[9]TANG Weiming,DENG Chenlong,SHI Chuang ,et al.Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J].GPS Solu,2013,10.

[10] FENG Yanming.GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J].J Geod,2008,82:847-862.

[11] LI Bofeng,FENG Yanming,SHEN Yunzhong.Three carrier ambiguity resolution: distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J].GPS Solut,2010,14:177-184.

[12] BANVILLE S,LANGLEY R B.Mitigating the impact of ionospheric cycle slips in GNSS Observations[J].J Geod,2013,87:179-193.

[13] ZHAO Qile, SUN Binzi, DAI Zhiqiang, et al. Real-time detection and repair of cycle slips in triple-frequency GNSS measurements[J].GPS Solut,2014,17:123-131.

[責任編輯：張德福]

An modified model for real-time cycle slip detection and repair in triple-frequency BDS measurements

GAO Jie1,2,XIE Jiantao3

(1.School of Geospatial Information，Information Engineering University，Zhengzhou 450001，China；2. Xi’ an Division of Surveying and Mapping，Xi’an 710054，China；3. School of Navigation and Space Engineering，Information Engineering University，Zhengzhou 450001，China)

Many carrier phase combinations with good characteristics can be got in BDS triple-frequency, which improves the effect of cycle slip detection and repair base on undifferenced observation .This paper presents a model for cycle slip detection and repair base on BDS triple-frequency undifferenced observation.Firstly, the HMW combination is used for EWL cycle slip detection and repair, then, geometry-free carrier phase combination with the repaired EWL and WL can be used to estimate WL cycle slip with neglecting the ionospheric delay. Finally, ionospheric delay variation can be updated by optimal carrier phase combinations, then, cycle slip in NL can be estimated by new geometry-free combination formed by the cycle-slip-fixed WL observation and NL observation. At last, cycle slips in original carrier phase observations can be estimated by simple transformation. Then the feasibility of the model is verified with the measured data, and the result shows that the model is feasible even in the condition of active ionospheric disturbance.

BDS; triple-frequency; cycle slip; ionospheric; optimal carrier combination

10.19349/j.cnki.issn1006-7949.2016.12.006

2015-12-30

國家自然科學基金資助項目(41574010)

高杰(1987-)，男，助理工程師，碩士研究生.

P207

A

1006-7949(2016)12-0025-07