具有Neumann邊界條件的非局部多孔體介質方程解的爆破時間下界估計*

方鐘波, 柴　艷

(中國海洋大學數學科學學院，山東 青島 266100)

?

具有Neumann邊界條件的非局部多孔體介質方程解的爆破時間下界估計*

方鐘波, 柴艷

(中國海洋大學數學科學學院，山東 青島 266100)

本文中研究一類具有非齊次Neumann邊界條件的非局部多孔體介質方程解的爆破現象。對邊界流為線性源及線性吸收情形，利用微分不等式技巧得到解發生爆破時爆破時間下界估計值。

多孔體介質方程；非局部源；Neumann邊界條件；爆破時間下界

引用格式：方鐘波, 柴艷. 具有Neumann邊界條件的非局部多孔體介質方程解的爆破時間下界估計[J]. 中國海洋大學學報(自然科學版), 2016, 46(9): 129-132.

FANGZhong-Bo，CHAIYan.Lowerboundsestimatesoftheblow-uptimeforanonlinearnonlocalporousmediumequationwithNeumannboundarycondition[J].PeriodicalofOceanUniversityofChina, 2016, 46(9): 129-132.

考慮一類具有非局部源與非齊次Neumann邊界條件的多孔體介質方程初邊值問題

ut=Δum+up∫Ωuqdx,(x,t)∈Ω×(0,T),

(1)

(2)

u(x,0)=u0(x),x∈Ω,

(3)

其中:Ω?R3是具有光滑邊界?Ω的有界區域;p≥0;q>0;p+q>m>1;k是常數;ν是?Ω上的單位外法線向量;T是可能發生爆破的時間。

方程(1)描述流體力學、人口動力學及生物群體力學等諸多領域中擴散現象[1-2]。從流體力學角度來說，描述牛頓流在多孔體介質中的流動，其中up∫Ωuqdx叫“非局部熱源”項，非線性邊界流(2)中系數k為正或負時分別稱為“線性源”或“線性吸收”邊界流。

對拋物型方程(組)解的爆破現象的研究已有許多文獻和專著，見文獻[3-4]及相關文獻。但是，這些文獻討論的問題是關于解的整體存在性與非存在性及漸近性質相關的問題。最近，此類問題中爆破解的爆破時間上下界估計值的計算方面也引起了許多學者和專家的廣泛關注。其實，爆破時間上界估計方面已有較好的成果，比如Levine[5]介紹的凸性方法，Gao等[6]介紹的輔助函數法、極值原理和上下解方法相結合的方法等。相對而言，爆破時間下界估計更難。Song[7]研究了研究了具有非局部源項和吸收項的半線性擴散方程

ut=Δu+∫Ωupdx-kuq, (x,t)∈Ω×(0,T),

其中p>q>1。他們利用微分不等式的技巧，在齊次Dirichlet邊界條件或齊次Neumann邊界條件下得到了爆破時間的下界。之后，Liu等[8]和Fang等[9]采用類似的方法，考慮了具有非局部源項和吸收項的擬線性拋物型方程，并得到了爆破時間下界估計值。

由上所知，具有非齊次Neumann邊界條件的非局部多孔體介質方程初邊值問題(1)～(3)中爆破解的爆破時間下界估計的研究還未得到展開。此類問題的難度在于文獻[7-9]中采用的微分不等式技巧不再適用于問題(1)～(3)等。本文，對邊界流為線性源及線性吸收情形，利用改進的微分不等式技巧得到爆破時間下界估計值。實際上，當p+q>m>1且初始值充分大時，類似于文獻[10]方法易得問題(1)～(3)解在有限時刻T爆破。

注意到，由Sobolev型不等式的最優化常數，導致所得的結果僅局限在三維空間，見文獻[13]。同時，此類問題的研究對于發展方程解的生命跨度的確定有著非常重要的意義。

1　當k>0時爆破時間T的下界

定義輔助函數

η(t)=∫Ωuα(p+q-1)dx,

(4)

η′(t)=α(p+q-1)∫Ωuα(p+q-1)-1utdx=

α(p+q-1)∫Ωuα(p+q-1)-1[Δum+up∫Ωuqdx]dx=

kα(p+q-1)∫?Ωuα(p+q-1)dS-

mα(p+q-1)[α(p+q-1)-1]∫Ωuα(p+q-1)+m-3

(5)

由積分等式

div(uα(p+q-1)x)=3uα(p+q-1)+α(p+q-1)uα(p+q-1)-1(x·▽u)

可得

(6)

再由Schwarz不等式得

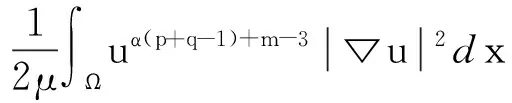
(7)

把(6)，(7)帶入(5)得

{mα(p+q-1)[α(p+q-1)-1]-

α(p+q-1)∫Ωuα(p+q-1)+p-1dx∫Ωuqdx。

(8)

利用H?lder不等式可知

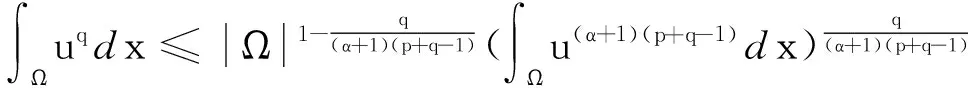
(9)

∫Ωuα(p+q-1)+p-1dx ≤

(10)

(11)

又

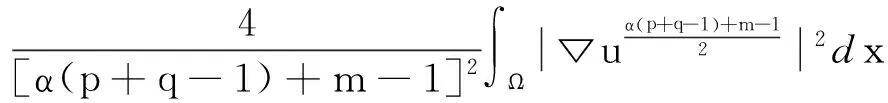
(12)

把(9)-(12)帶入(8)有

(13)

其中

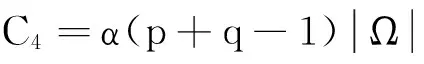
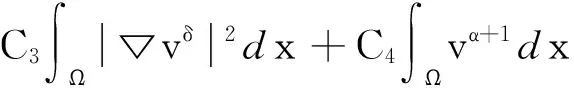
(14)

(15)

類似于[12]中(2.28)式的推導得

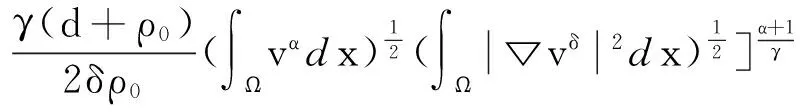
(16)

用H?lder不等式得

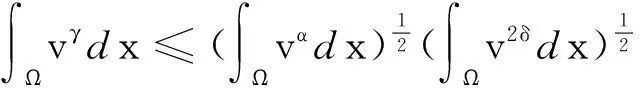
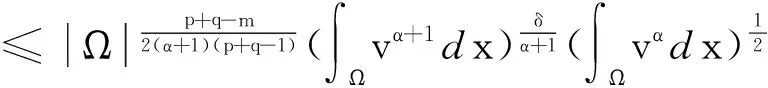
(17)

把(17)帶入(16)且應用下列不等式

得

(18)

由(15)及(18)可知

∫Ωvα+1dx≤

(19)

∫Ωvα+1dx≤

(20)

其中κ1，κ2>0待定。由(20)可以得出

(21)

其中

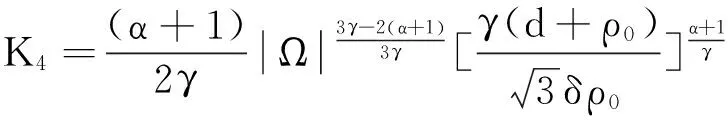
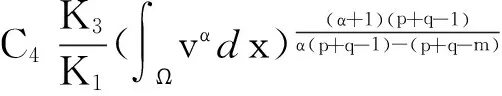
(22)

記

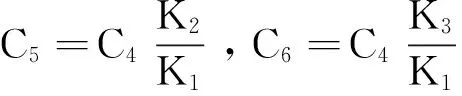
則(22)式可簡寫成

(23)

在(0,t)積分(23)得

其中

2　當k≤0時爆破時間T的下界

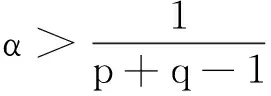
對η(t)求導，并由(2)及k≤0，可得

η′(t)=α(p+q-1)∫Ωuα(p+q-1)-1utdx=

α(p+q-1)∫Ωuα(p+q-1)-1[Δum+up∫Ωuqdx]dx=

kα(p+q-1)∫?Ωuα(p+q-1)dS-

mα(p+q-1)[α(p+q-1)-

α(p+q-1)∫Ωuα(p+q-1)+p-1dx∫Ωuqdx≤

-mα(p+q-1)[α(p+q-1)-

(24)

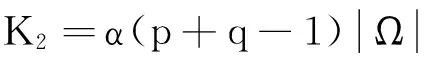
類似于定理1的證明過程，可得

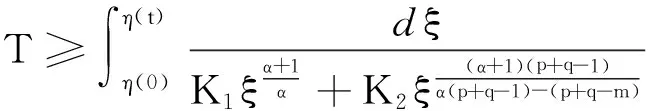
因此，可以建立下面的定理。

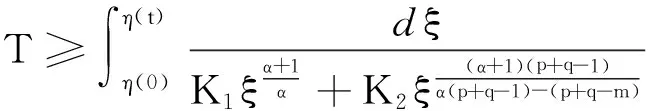
[1]Bebernes J ，Eberly D. Mathematical Problems from Combustion Theory [M]. New York：Springer-Verlag, 1989.

[2]Wu Z, Zhao J, Yin J，et al. Nonlinear Diffusion Equations [M].Singapore: World Scientific, 2001.

[3]Levine H A. The role of critical exponents in blow-up theorems [J]. SIAM Rev, 1990, 32: 262-288.

[4]Samarskii A A, Kurdyumov S P, Galaktionov V A , et al. Blow-up in Problems for Quasilinear Parabolic Equations [M]. Moscow: Nauka, 1987, Berlin: Walter de Gruyter, 1995.

[5]Levine H A. Nonexistence of global weak solutions to some properly and improperly posed problems of mathematical physics: The method of unbounded fourier coefficients [J]. Math Ann, 1975, 214: 205-220.

[6]Gao X, Ding J, Guo B Z. Blow up and global solutions for quasilinear parabolic equations with Neumann boundary conditions [J]. Applicable Analysis, 2009, 88: 183-191.

[7]Song J C. Lower bounds for the blow-up time in a non-local reaction-diffusion problem [J]. Applied Mathematics Letter, 2011,24: 793-796.

[8]Liu D, Mu C, Xin Q. Lower bounds estimate for the blow-up time of a nonlinear porous medium equation [J]. Acta Mathematica Scientia, 2012, 32B(3): 1206-1212.

[9]Fang Z B, Yang R, Chai Y. Lower bounds estimate for the blow-up time of a slow diffusion equation with nonlocal source and inner absorption [J]. Mathematical Problems in Engineering, 2014 ,42: ID764248: 6.

[10]Li F, Xie C. Global existence and blow-up for a nonlinear porous medium equation [J]. Appl Math Lett, 2003, 16: 185-192.

[11]Talenti G. Best constant in Sobolev inequality [J]. Ann Mat Pura Appl, 1976, 110(1): 353-372.

[12]Li Y, Liu Y , Lin C. Blow-up phenomena for some nonlinear parabolic problems under mixed boundary conditions [J]. Nonliner Anal Real World Appl, 2010, 11: 3815-3823.

AMSSubjectClassifications：35R45; 35K65

責任編輯陳呈超

Lower Bounds Estimates of the Blow-up Time for a Nonlinear NonlocalPorousMediumEquationwithNeumannBoundaryCondition

FANGZhong-Bo，CHAIYan

(SchoolofMathematicalSciences,OceanUniversityofChina,Qingdao266100,China)

Inthispaper,theblow-upphenomenaofanonlinearnonlocalporousmediumequationwithnonhomogeneousNeumannboundaryconditionareinvestigated.Byusingadifferentialinequalitytechnique,lowerboundsestimatesoftheblow-uptimeareobtainedwhenboundaryfluxislinearsourceorlinearabsorption.

porousmediumequation;nonlocalsource;Neumannboundarycondition;thelowerboundofblow-uptime

山東省自然科學基金項目(ZR2012AM018)；中央高校基本科研基金項目(201362032)資助

2014-03-20；

2014-10-12

方鐘波(1968-)，男，教授。E-mail:fangzb7777@hotmail.com

O175

A

1672-5174(2016)09-129-04

10.16441/j.cnki.hdxb.20140082

SupportedbytheNaturalScienceFoundationofShandongProvinceofChina(ZR2012AM018)andtheFundamentalResearchFundsfortheCentralUniversity(201362032)