正則化方法在結構模型修正中的應用研究*
李英超, 王樹青, 張 敏
(1.魯東大學土木工程學院,山東 煙臺 264025; 2.中國海洋大學工程學院,山東 青島 266100)
?
研究簡報
正則化方法在結構模型修正中的應用研究*
李英超1, 王樹青2, 張敏2
(1.魯東大學土木工程學院,山東 煙臺 264025; 2.中國海洋大學工程學院,山東 青島 266100)
大型結構的模型修正求解問題多呈現不同程度的病態,實測數據的微小誤差都有可能造成求解的失效。該文研究了測量噪聲影響下模型修正病態系統的求解問題。首先,介紹了結構模型修正的求解問題以及數學上常用的正則化方法;然后,通過一懸臂梁模型數值算例探討了截斷奇異值分解正則化方法和“L”曲線法在結構模型修正求解中的適用性。結果顯示,適當的正則化可以有效的解決模型修正病態系統的求解問題;另外,該方法對于部分滿足離散Picard條件的模型修正方程同樣適用。最后,通過一導管架平臺物理模型試驗對該正則化方法的實用性進行了驗證。
模型修正; 病態;正則化;導管架平臺
引用格式:李英超, 王樹青, 張敏. 正則化方法在結構模型修正中的應用研究[J]. 中國海洋大學學報(自然科學版), 2016, 46(9): 107-115.
LI Ying-Chao, WANG Shu-Qing, ZHANG Min. Study on the application of regularization method in structural model updating[J]. Periodical of Ocean University of China, 2016, 46(9): 107-115.
一個反應實際的有限元模型是進行結構計算分析和安全評估的基礎。然而在實際工程中,有限元模型與實際結構之間往往存在差異,解決這一問題的常用方法是模型修正[1]。
近年來,隨著模型修正方法的日趨成熟,學者和工程師們將其應用到了橋梁[2-3]、房屋[4]和海洋平臺[5-7]等土木工程領域。然而,大量研究表明,簡單的將現有的模型修正方法應用到海洋平臺、橋梁等復雜的結構上,效果并不理想。究其原因:從技術本身來講,動力模型修正是結構動力學的反問題,修正方程常呈現病態,實測數據的微小誤差將會引起解的“振蕩”;另外模型修正方程的解往往具有非唯一性,此時只能通過估計方法給出最優解,估計誤差的大小與方程的病態性以及實測信息的數量和精度直接相關[8]。從工程角度來講,海洋平臺等三維結構在建模中通常需要進行大量的簡化,實際結構參數的不確定性較多;另外,受工作環境限制,實測信息量非常有限,且受噪聲污染較嚴重。因此,研究實測數據含噪聲情況下模型修正病態方程組的求解問題,對于模型修正方法推向工程應用具有重要的意義。
上述病態方程組的求解問題在數學領域并不罕見,常用的手段是正則化方法。最早的正則化方法由Tikhonov[9]提出,通過正則化參數的選擇,使得正則解在最小二乘解和最小范數解之間取得平衡,從而控制解的振蕩和修正的擬合程度。目前最常用的正則化方法主要依據矩陣的奇異值分解(SVD)技術,如截斷奇異值分解(TSVD)方法[10-12]。文獻[8]對各種正則化方法進行了較系統深入的研究,針對不同規模的病態系統提出了適用的正則化方法,并指出利用正則化方法求解不適定問題的關鍵是正則化參數的選擇,這一過程通常需要借助一些數學統計手段,如Morozov偏差準則,廣義交叉檢驗法, “L”曲線法等,這些方法均需要進行大量的試算。
正則化方法盡管在理論上比較完善,但在模型修正的實際應用中卻仍然存在一些問題,如對于不同問題,同一算法表現出的收斂性卻不同,很難用一個通用的方法解決不適定問題[13]。
本文將數學上常用的TSVD正則化方法和“L”曲線法引入到結構模型修正線性方程組的求解中,然后通過一懸臂梁數值算例來探討該方法的適用性,最后通過一海洋平臺物理模型試驗對該方法的實用性作進一步驗證。研究中,模型修正線性方程組的構建方法采用文獻[14]提出的交叉模型交叉模態方法,受篇幅限制,不再對該方法進行詳細介紹。
1 模型修正求解問題
現有的模型修正方法,雖然思路不盡相同,但大多可歸結為線性方程組
Ax=b
(1)
根據m和n的大小關系,式(1)所示線性方程組有三種情況:
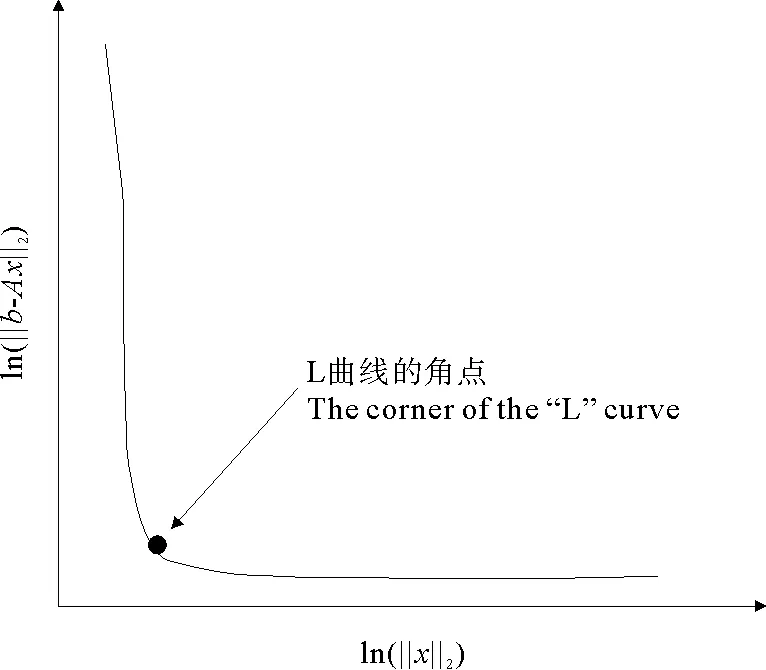
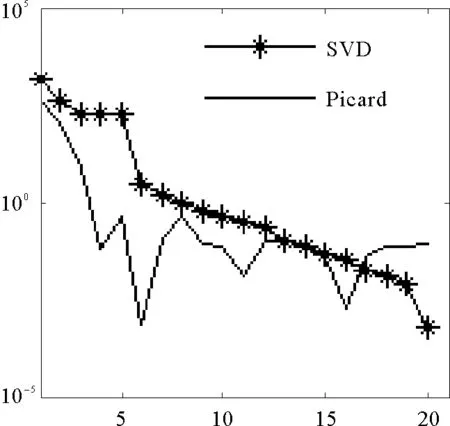
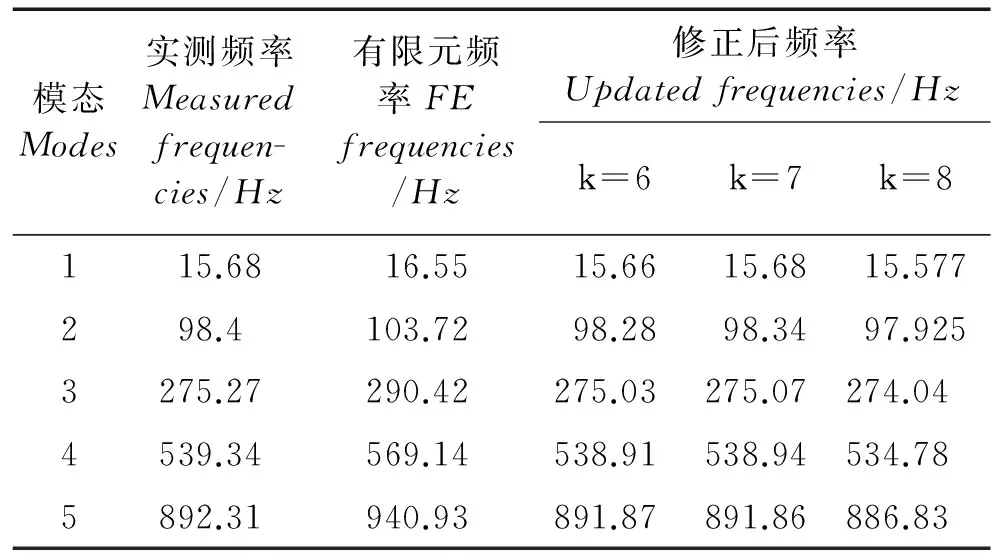
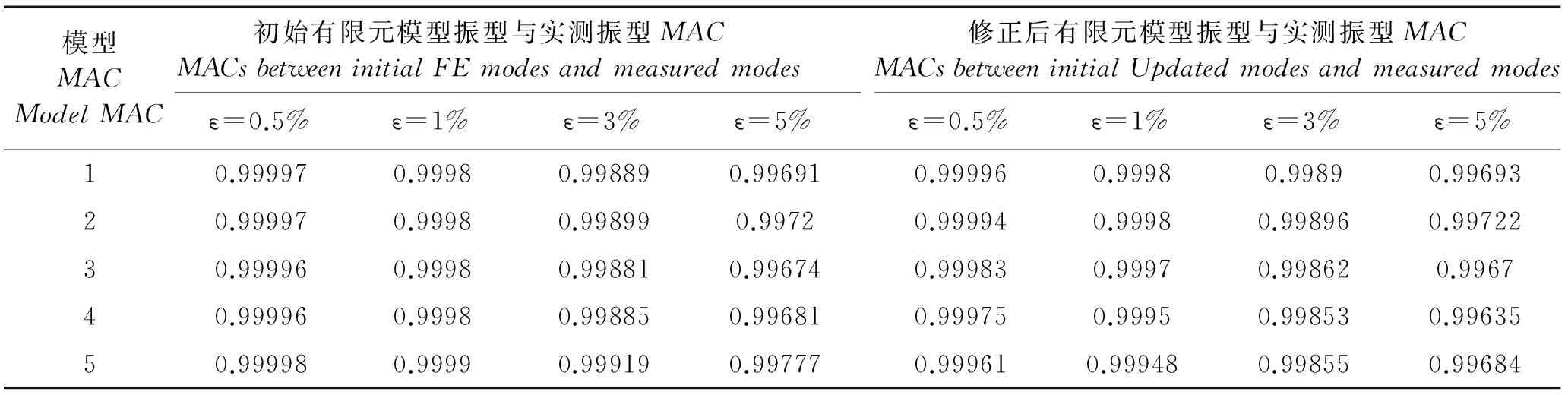
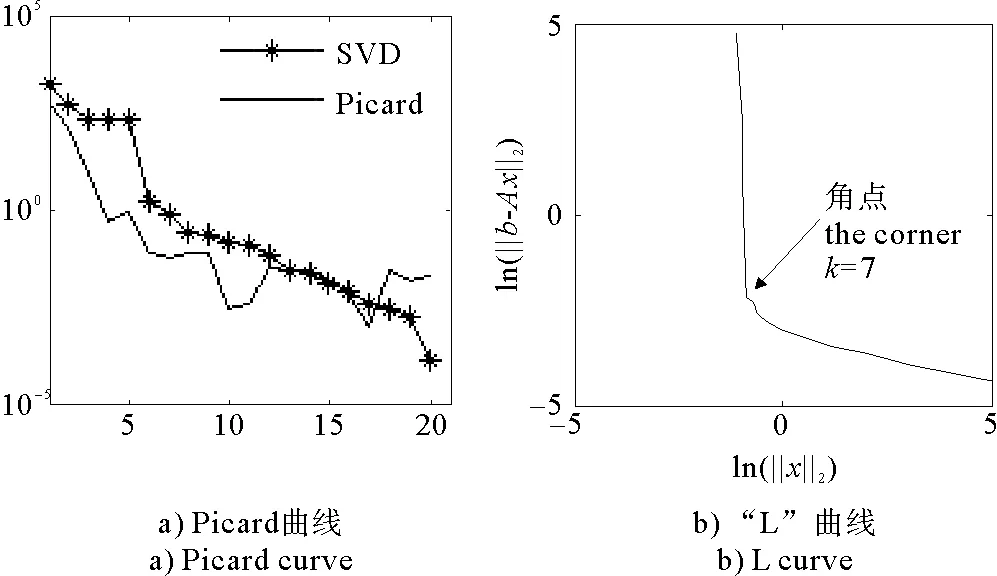
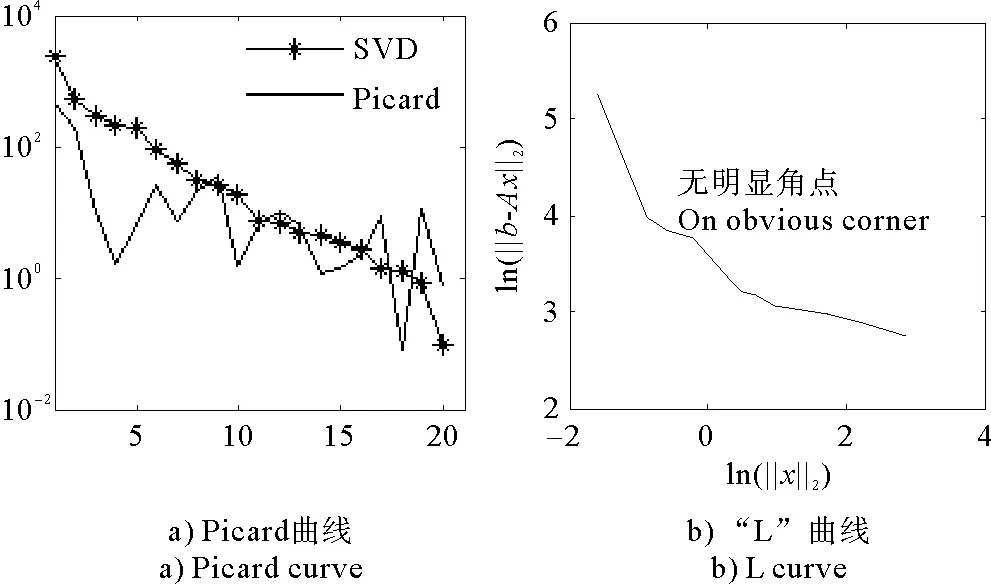
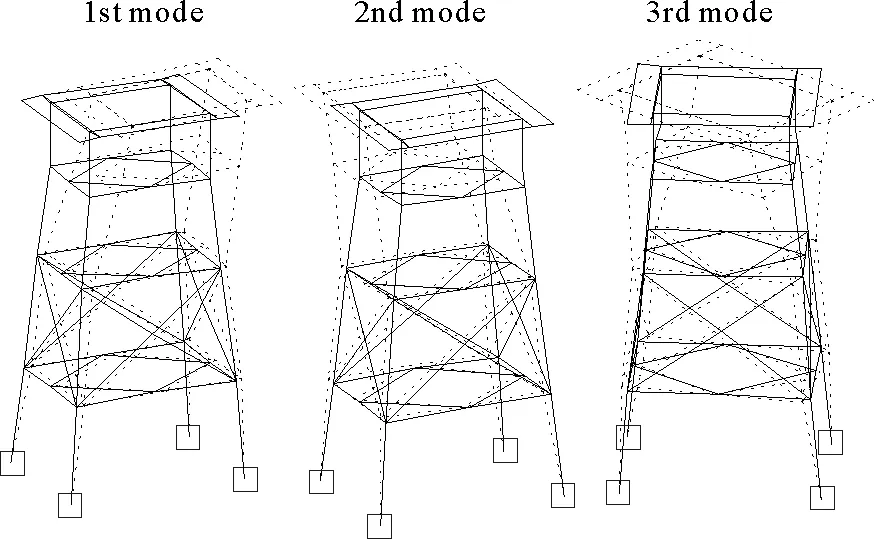
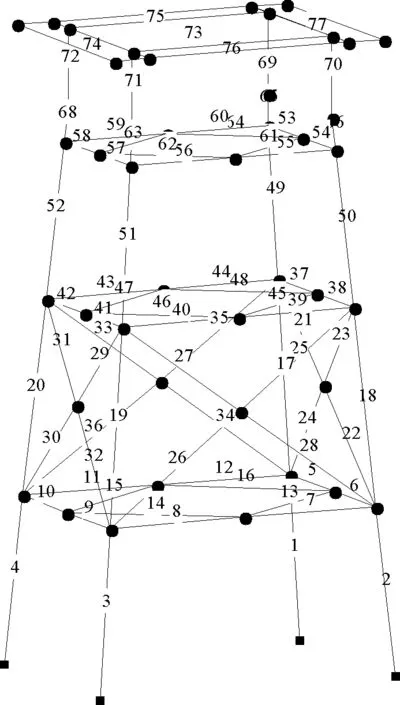
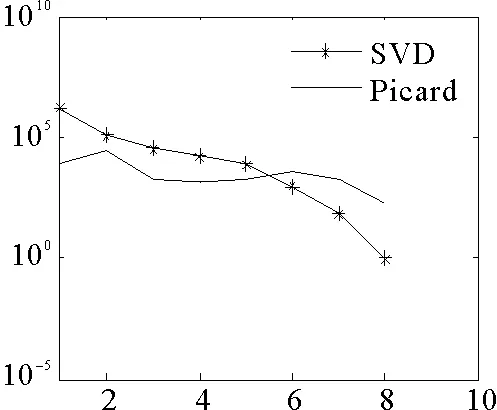
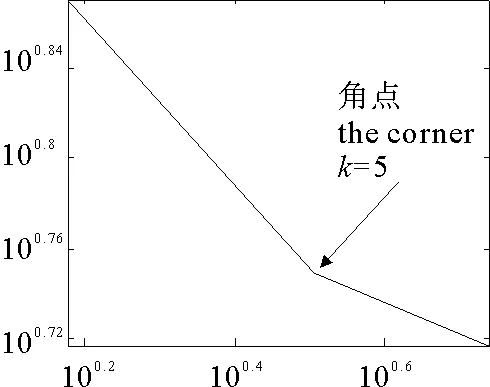
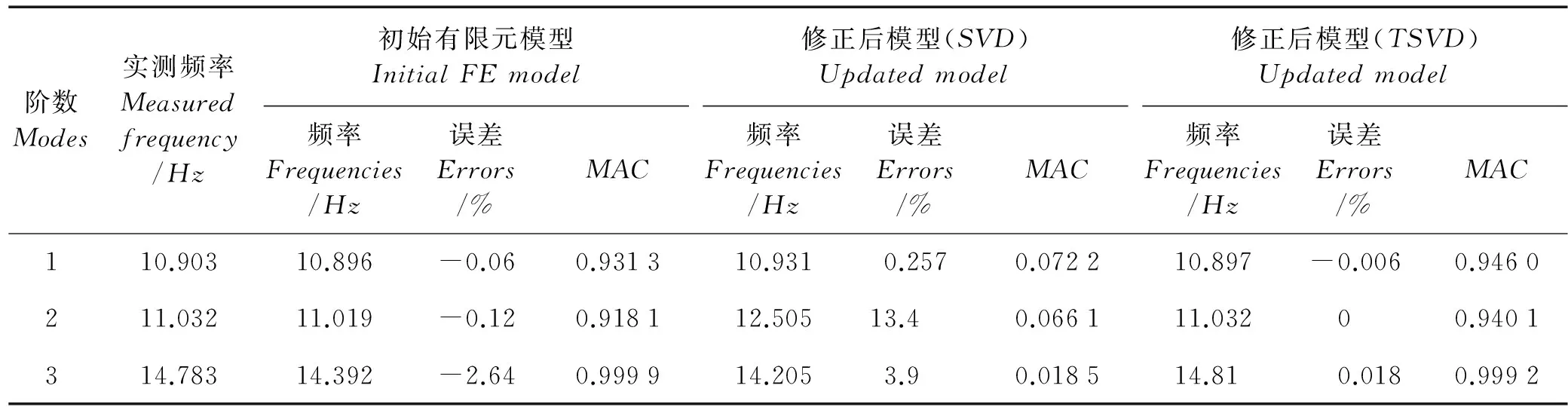
(1)當rank(A) (2)當rank(A)=n,m=n,稱為適定系統,可通過標準求逆來進行求解,x=A-1b; (3)當rank(A)=n,m>n,稱為超定系統,通常采用最小二乘解來逼近真實解; 而多數實際問題均屬于欠定系統、超定系統或者兩種系統的組合,稱為混合待定系統。對于各類問題,比較通用的求解方法是奇異值分解法(SVD)。 對式(1)的系數矩陣A做奇異值分解: A=UΣVT。 (2) (3) 其中對角陣Σr=diag(σ1,σ2,…,σr)的對角元素為矩陣A的奇異值,且滿足σ1≥σ2≥…≥σr>0,r為A的秩。 將酉矩陣U和V分別記為U=(u1,u2,…,um),V=(v1,v2,…,vn),其中u1,u2,…,um和v1,v2,…,vn分別為酉矩陣U和V的列向量,則(2)式可寫為 (4) 方程(1)的解可寫為: (5) 當有限元自由度較大,修正參數較多且靈敏度差異較大時,模型修正方程組多呈現不同程度的病態,測量數據含有噪聲時,會導致該線性方程組的求解發生“振蕩”,很難得到有物理意義的修正結果。通常可以通過系數矩陣的條件數來判斷其病態性,即最大奇異值與最小奇異值之比。條件數越大,系統的病態性越強,解越不穩定。 測量噪聲影響下病態方程組的求解是一個難點問題。Hansen[15]指出,對于式(1)所示線性方程組,如果滿足以下3個條件,則可以通過正則解來逼近精確解。 (1)矩陣A的條件數非常大; (2)矩陣A的奇異值逐漸下降趨于零; 通常可以畫出系數矩陣A的奇異值曲線(SVD曲線)和離散傅里葉系數曲線(Picard曲線),當SVD曲線在Picard曲線上方時,表示滿足該條件;當在下方或重合時即不滿足該條件。離散Picard條件的物理意義在于檢驗線性系統的病態性及受噪聲污染的程度。 本節介紹病態線性方程組求解中常用的兩種正則化(Regularization)方法:吉洪諾夫(Tikhonov)[9]正則化方法和截斷奇異值法(TSVD)[11-12]。 2.1 吉洪諾夫(Tikhonov)正則化方法 對于不適定的修正方程組,最小二乘解的目標是使修正后模型得到最好的擬合,但對某些參數,會出現解的振蕩,從而失去物理意義;而最小范數解可以避免出現解的振蕩,但其修正擬合效果較差。 (6) 其中Γ為Tikhonov正則化矩陣,通常為微分算子或加權傅里葉算子的離散形式,用以保證解的光滑性。一般取Γ=I或Γ=αI,其中α被稱為正則化參數,用于控制最小二乘解和最小范數解之間的平衡。當α值較大時,可以保證‖x‖值較小,但可能會導致解不滿足Ax=b;反之,如果α值較小,雖然能得到滿足方程組的解,但該解會發生振蕩,使得模型修正失去物理意義。α通常取為A的某個奇異值,它的取值對求解非常關鍵。 假定A的奇異值分解為(4),則方程組(1)的正則解可寫為 (7) 其中, (8) 稱為Tikhonov因子,它依賴于奇異值σi和正則化參數α。當f(σi)為1時,式(7)即為(5)。由此可見,非零α的作用是過濾掉小奇異值對解的貢獻,從而起到穩定解的作用。 2.2 截斷奇異值分解(TSVD)正則化方法 截斷奇異值法直接舍棄式(5)中的小奇異值。即取過濾因子為: (9) 如果取σ1≥…≥σk≥α≥σk+1≥…≥σr≥0,則正則解為 (10) 其中k稱為截斷數,當k=rank(A)時,式(10)即為式(5)所示最小二乘解。 截斷奇異值法等價于用矩陣 (11) 來近似系數矩陣A。 TSVD正則化方法是Tikhonov正則化方法的一個特例,該過程直接舍棄了小奇異值對解的貢獻,一般適用于系數矩陣A的奇異值呈階梯型分布病態問題[16]。對于桿系結構有限元模型修正問題,其方程組系數矩陣的奇異值多呈階梯型分布,因此在本文研究中選用TSVD正則化方法進行研究。 2.3 正則化參數的選取 當系統滿足離散Picard條件時,對于正則化參數α∈(0,∞)或k∈(1,r),曲線(ln(‖Γx‖2),ln(‖b-Ax‖2))形狀呈“L”型,被稱為“L”曲線,如圖1所示,其角點正好使得最小二乘解和最小范數解得到平衡。因此可通過畫出“L”曲線來選擇正則化參數。如當采用TSVD正則化方法時,可通過該曲線的最大曲率來確定角點,從而確定截斷數k。 圖1 “L”曲線圖 “L”曲線法選取正則化參數的物理意義明確,應用簡單,因此本文選擇該方法進行適用性探討。 本節通過一懸臂梁模型數值算例,將TSVD正則化方法應用到模型修正線性方程組的求解中,通過與基于SVD的最小二乘解修正結果比較,探討該正則化方法在該類模型修正中的適用性。 3.1 模型介紹 一鋼制二維懸臂梁長1m,彈性模量E=2.06×1011N/m2,密度為ρ=7 850kg/m3,截面為30mm×20mm。將梁均勻劃分為20個單元,如圖2所示,共有21個節點,其中一個節點固定,共有60個自由度。通過特征值分解可以得到其模態頻率和振型。 圖2 懸臂梁模型 算例中實測模型是通過修改有限元模型各單元的剛度矩陣來進行模擬的。假定實測模型與有限元模型相比各單元間有均值為0.1,標準差為0.01,且呈正態分布的的剛度誤差。通過特征值分解,得到修改后模型的模態頻率和振型來模擬實測模型的模態參數。 由于在模態測試中,模態頻率的識別結果一般較準確,而振型的識別結果常常受測量噪聲的影響較嚴重,因此在本算例中假定實測模態振型含有噪聲。為探討正則化方法的實用性,本算例首先設定噪聲水平為1%,添加方式為φi,j=φi,j(1+εRi,j),其中ε為噪聲水平;Ri,j為均值為0,方差為1的高斯隨機數,φi,j為對應于第i個自由度的第j階振型值。即在通過數值模擬獲得的實測模態振型的基礎上添加一定水平的高斯白噪聲。 有限元模型與實測模型的前5階模態對比如表1所示,頻率誤差均大于5%,振型吻合程度較好。 3.2 基于SVD的最小二乘解修正 利用CMCM方法對20個單元的剛度矩陣進行修正,修正系數取各個單元的彈性模量。取前5階實測模態和前5階有限元分析模態,建立模型修正的線性系統Ax=b;其中,size(A)=25×20;cond(A)=2.6536×106;rank(A)=20,與未知數的個數相等,因此理論上有解。 用奇異值分解法(SVD)求取方程組的最小二乘解,并對有限元模型進行修正,結果如表1所示。修正后有限元模型的頻率會出現虛數,振型MAC值嚴重偏離1,因此基于SVD的最小二乘解會導致沒有物理意義的修正。 導致以上結果的主要原因是系數矩陣A的條件數較大(cond(A)= 2.6536×106),方程組呈現一定程度的病態,在測量噪聲的影響下,最小二乘解發生“振蕩”,遠遠偏離真實值,導致模型修正失去物理意義。 表1 基于SVD的最小二乘解修正結果 3.3基于TSVD的正則解修正 對于3.2中構建的線性系統Ax=b,畫出其Picard曲線(其中SVD表示奇異值曲線和Picard表示傅里葉系數曲線),如圖3所示。可以看出,矩陣A的奇異值逐漸趨向于零;但從第17個奇異值開始,不能滿足離散Picard條件。因此該方程組滿足可正則化求解的前兩個條件,但只能部分滿足第三個條件(離散Picard條件)。 圖3 Picard曲線圖(ε=1%) 對于以上部分滿足離散Picard條件的模型修正線性方程組,本文嘗試采用TSVD正則化方法進行求解,并用“L”曲線法選取截斷數k。 通過大量試算,畫出該系統的“L”曲線,如圖4所示。將“L”曲線上位于角點左側最靠近的點選為截斷數,此時k=7。 圖4 “L”曲線圖(ε=1%) 根據式(10)求出該方程的正則解,并對初始模型進行修正,結果如表3和4所示(ε=1%工況對應結果)。通過比較可以發現,基于正則化求解的模型修正效果很好。由此說明,對于部分滿足離散Picard條件的模型修正線性方程組,同樣可正則化求解。 為驗證“L”曲線法對截斷數選取的有效性,分別取k=6, k=8兩種情況來進行模型修正,結果如表2所示。通過比較發現,截斷數取7時修正效果最好。說明“L”曲線法對于截斷數的選取是適用的。 表2 不同截斷數的模型修正結果比較 3.4 TSVD正則化方法的噪聲魯棒性探討 為探討TSVD正則化求解方法在不同測量噪聲水平下的適用性,本部分增加五種噪聲工況:0.5%、 3%、5%、10%和20%進行對比研究。修正方程組的構建方式和噪聲添加方式同上。 采用奇異值分解法(SVD)進行求解,并對有限元模型進行修正,各噪聲工況下結果類似于3.2,修正后有限元模型的頻率會出現虛數,振型MAC值會更差,因此最小二乘解會導致沒有物理意義的修正。 分別畫出各噪聲工況下的Picard曲線和“L”曲線,如圖5~9,通過比較可以看出,隨著噪聲水平的提高,方程組對離散Picard條件的滿足程度逐漸降低。另外 “L”曲線逐漸趨于平滑,當噪聲水平達到10%、20%時,很難通過“L”曲線選定截斷數k,如圖8~9所示。但對于能夠通過“L”曲線選定出截斷數的4個噪聲工況,均可以通過TSVD方法獲得較理想的修正結果,如表3~4所示。 表3 基于TSVD正則解的模型修正結果(模態頻率) 表4 基于TSVD正則解的模型修正結果(模態振型) 圖5 Picard曲線和“L”曲線(ε=0.5%) 圖6 Picard曲線和“L”曲線(ε=3%) 圖7 Picard曲線和“L”曲線(ε=5%) 圖8 Picard曲線和“L”曲線(ε=10%) 圖9 Picard曲線和“L”曲線(ε=20%) 4.1 模型試驗 試驗模型為某導管架平臺的縮尺簡化模型,如圖6所示。材料為鋼材,除導管腿選用Φ20mm×2mm鋼管外,其它桿件均為Φ10mm×2mm的鋼管。由下而上各層高度分別為:0.41m,0.88m,1.25m和1.53m;工作點高度為1.33m。各層橫撐平面尺寸分別為:基底,0.77m×0.54m;一層,0.693m×0.487m;二層,0.6m×0.424m;三層,0.535m×0.375m;工作點以上, 0.52m×0.365m。甲板采用700mm×545mm×10mm的鋼板模擬,柱腳采用螺栓固定。 為模擬在役平臺的不同損傷工況,立柱、斜撐和橫撐均設有局部損傷件(如圖10中帶有替換件位置,分別對應于有限元模型的25、51和60單元)。 圖10 鋼質導管架模型及測試儀器 測試采用加速度傳感器,信號(經內部放大)直接接入PL16-DCB8 數據采集儀,然后通過網線接入電腦。傳感器布置方案如圖11所示,共有62個自由度進行了測試。在模型試驗中,采用力錘敲擊頂層甲板角部,同時激發兩個方向的彎曲模態和扭轉模態。由特征系統實現算法(ERA)識別到的結構前三階頻率分別為:10.9026Hz,11.0321Hz和14.7827Hz。模態測試其它詳細過程可參見文獻[6]。 圖11 傳感器布置示意圖 采用文獻[10]中介紹的最優擬合法對實測模態進行插值擴階,振型圖如圖12所示。 圖12 實測振型 4.2 有限元模型 應用Matlab編程,建立該試驗模型的有限元模型如圖13所示。桿件采用兩節點三維梁單元,導管架中每根桿劃分為1個單元,共計72個桿單元;甲板采用四節點殼單元,共劃分為5個單元。彈性模量取為E=2.06×1011N/m2,密度ρ=7 850kg/m3,采用一致質量矩陣。通過特征值分解,得到有限元模型的模態頻率和振型。通過表5中有限元模態與實測模態的對比可以看出,第三階模態誤差相對較大。 圖13 導管架平臺有限元模型 4.3 有限元模型修正 (1) 修正參數選擇 通過試算發現,在總質量一定的條件下,甲板的單元劃分及質量矩陣的構建方法,對第3階頻率影響較大。對于本模型,雖然甲板總質量是確定的,但在有限元模型中只劃分了五個單元(如圖13中73~77單元),且大小不一,勢必會造成較大的建模誤差。另外由于替換件的設置,局部法蘭連接亦會造成實際模型與有限元模型之間的誤差。 因此,可以初選甲板73~77單元的質量矩陣,以及25、51和60單元的剛度矩陣作為修正對象,修正參數為相應的質量修正系數β74, β75, β76, β77和剛度修正系數α25, α51, α60,共8個。 (2)模型修正 用前3階實測模態和前5階有限元分析模態構建15個CMCM方程,方程組系數矩陣的秩為8,求解8個未知數,理論上有唯一解。 采用SVD方法求取修正方程組的最小二乘解,并對有限元模型進行修正,結果如表5所示,修正后模型的的頻率和振型與實測值吻合程度比初始有限元模型更差,修正求解失效。 由該方程組的Picard曲線(如圖14所示)可以看出,該系統滿足可正則求解的前兩個條件,部分滿足離散Picard條件,因此可考慮采用TSVD正則化方法進行求解。 圖14 Picard曲線 采用L曲線法選取截斷數k=5(如圖15所示)。根據公式(10)求取該方程組的正則解,并對有限元模型進行修正,結果如表5所示。修正后模型的前三階頻率和振型均有所改善,尤其對于初始誤差較大的第三階模態,修正效果較好。 圖15 “L”曲線 階數Modes實測頻率Measuredfrequency/Hz初始有限元模型InitialFEmodel頻率Frequencies/Hz誤差Errors/%MAC修正后模型(SVD)Updatedmodel頻率Frequencies/Hz誤差Errors/%MAC修正后模型(TSVD)Updatedmodel頻率Frequencies/Hz誤差Errors/%MAC110.90310.896-0.060.931310.9310.2570.072210.897-0.0060.9460211.03211.019-0.120.918112.50513.40.066111.03200.9401314.78314.392-2.640.999914.2053.90.018514.810.0180.9992 本文對模型修正病態方程組的求解問題進行了探討,將數學上常用的TSVD正則化方法和“L”曲線法引入到了模型修正線性方程組的求解中,通過數值和試驗研究得出以下結論: (1)當模型修正方程組呈現一定程度的“病態”時,在測量噪聲的影響下,最小二乘解容易導致模型修正失效。采用TSVD正則化方法進行求解可有效的解決這一問題; (2)模型修正線性方程組通常只能部分滿足離散Picard條件,TSVD正則化方法對此同樣適用; (3)TSVD正則化方法求解的關鍵是截斷數的選取,本文研究證明“L”曲線法對于截斷數的選取是有效的,但曲線的繪制過程需要進行大量的試算。 (4)當噪聲水平較大時,“L”曲線趨于平直,很難通過“L”曲線法對截斷數進行選取,因此尚需要探討其它方法。 [1]FriswellMI,MottersheadJE.FiniteElementModelUpdatinginStructureDynamics[M].Netherlands:KluwerAcademicPublishers, 1995: 2-3. [2]方志, 唐盛華, 張國剛, 等. 基于多狀態下靜動態測試數據的斜拉橋模型修正[J]. 中國公路學報, 2011, 24(1): 34-41 FangZhi,TangShenghua,ChenSujun,DongYou.Cable-stayedbridgemodelupdatingbasedonstaticanddynamictestdataofmulti-state[J].ChinaJournalofHighwayandTransport, 2011, 24(1): 34-41 [3]RibeiroD,CalcadaR,DelgadoR,etal.Finiteelementmodelupdatingofabowstring-archrailwaybridgebasedonexperimentalmodalparameters[J].EngineeringSructures, 2012, 40: 413-435. [4]ShiradhonkarSR,ManishShrikhande.Seismicdamagedetectioninbuildingframeviafiniteelementmodelupdating[J].ComputersandStructures, 2011, 89: 2425-2438. [5]MojtahediA,LotfollahiYaghinMA,HassanzadehY,etal.DevelopingarobustSHMmethodforoffshorejacketplatformusingmodelupdatingandfuzzylogicsystem[J].AppliedOceanResearch, 2011, 33: 398-411 [6]李英超. 基于模態參數識別的海洋平臺結構模型修正技術研究[D]. 青島: 中國海洋大學, 2012. LiYingchao.Modelupdatingofoffshoreplatformstructuresbasedonmodalparameteridentification[D].Qingdao:OceanUniversityofChina, 2012. [7]WANGS.,LIY,LIH.StructuralModelUpdatingofanOffshorePlatformUsingtheCrossModelCrossModeMethod:AnExperimentStudy[J].OceanEngineering, 2015, 97: 57-64. [8]吳頡爾. 正則化方法及其在模型修正中的應用[D]. 南京: 南京航空航天大學, 2007. WUJie-er.Theregularizationmethodwithapplicationtofiniteelementmodelupdating[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics, 2007. [9]AN.Tikhonov.Solutionofincorrectlyformulatedproblemsandtheregularizationmethod[J].SovietMath,Dokl, 1963, 4: 1035-1038. [10]C.Mares,MI.Friswell,JE.Mpttershwad.Modelupdatingusingrobustestimation[J].MechanicalSystemsandSignalProcessing, 2002, 16(1): 169-183. [11]MI.Friswell,JE.Mottershead,H.Ahmadian,Finite-elementmodelupdatingusingexperimentaltestdata:parametrizationandregu1arization[J].Phil.Trans.R.Soc.Lond. 2001, 359: 169-186. [12]CalvettiD,ReichelL,SgallariFandSpalettaG.Aregularizinglanczositerationmethodforunderdeterminedlinearsystems[J].JournalofComputationalandAppliedMathematics, 2000, 115: 101-120. [13]肖庭延, 于慎根, 王彥飛. 反問題的數值解法[M]. 北京: 科學出版社, 2003. XIAOTingyan,YUShengen,WANGYanfei.Numericalsolutionofinverseproblem[M].Beijing:SciencePress, 2003. [14]HuS-L.J.,LiH.,andWang,S.Cross-modelcross-modemethodfordynamicsystems[J].MechanicalSystemsandSignalProcessing, 2007, 21(4): 1690-1703. [15]HansenPC.Thediscretepicardconditionforill-posedproblems[J].BIT, 1990, 30: 658-672. [16]王振杰. 大地測量中不適定問題的正則化解法研究[D]. 北京: 中國科學院測量與地球物理研究所, 2003. WangZhenjie.Researchontheregularizationsolutionsofill-posedproblemsingeodesy[D].Beijing:InstituteofGeodesyandGeophysicsofChineseAcademyofSciences, 2003. 責任編輯陳呈超 Study on the Application of Regularization Method in Structural Model Updating LIYing-Chao1,WANGShu-Qing2,ZHANGMin (1.CollegeofCivilEngineering,LudongUniversity,Yantai264025,China; 2.CollegeofEngineering,OceanUniversityofChina,Qingdao266100,China) Whilemodelupdatingequationsoflargestructuresalwayspresentsill-conditioning,smallerrorsinthemeasureddatawouldcauseafailuresolution.Inthispaper,thesolutionproblemofill-conditionedandnoisypollutedmodelupdatingequationsisstudied.First,theregularizationmethodscommonlyusedinmathematicsareintroducedtosolvethemodelupdatingequations.Then,numericalexampleofancantileverbeamisstudiedtodiscusstheapplicabilityoftheregularizationmethod.Resultsshowthattheill-conditionedmodelupdatingsystemcanbesolvedeffectivelywithproperregularization.Inaddition,themethodcanalsobeappliedtothemodelupdatingequationswhichpartiallysatisfiesthediscretePicardcondition.Finally,anexperimentstudyofajacketplatformstructureisconductedtoverifythepracticabilityoftheregularizationmethod. modelupdating;ill-condition;regularization;jacketplatform 國家自然科學基金項目(51379196;51209189);山東省自然科學基金項目(ZR2013EEQ006);泰山學者工程專項經費;魯東大學科研基金項目(LY2013027)資助 2015-03-20; 2015-12-15 李英超(1985-),女,博士,講師。E-mail:yingchao.ouc@163.com O302;O327 A 1672-5174(2016)09-107-09 10.16441/j.cnki.hdxb.20150032 Supported by the National Natural Science Foundation of China(51379196;51209189); Natural Science Foundation of Shandong Province(ZR2013EEQ006); Taishan Scholars Program of Shandong Province ; Science Foundation of Ludong University(LY2013027)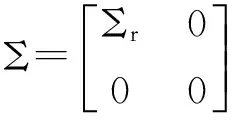
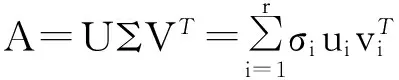
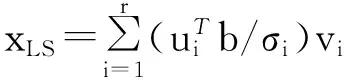
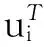
2 正則化方法
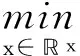
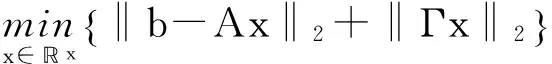
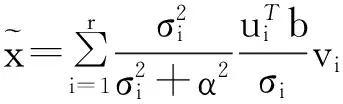

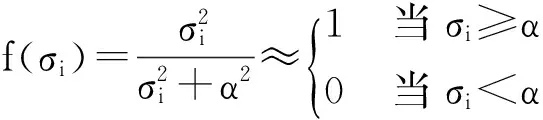
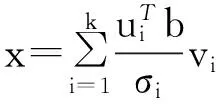

3 懸臂梁模型數值研究






4 導管架平臺物理模型試驗研究


5 結論

