理想聲自導魚雷運動要素的距離方位觀測解算方法
李長文,初 磊
(海軍潛艇學院,山東 青島 266199)
?
理想聲自導魚雷運動要素的距離方位觀測解算方法
李長文,初磊
(海軍潛艇學院,山東 青島 266199)
為快速預測魚雷的聲自導彈道,以特定時刻相對本艦的距離、舷角為運動要素,將其彈道參數(shù)化為以此要素為初值的微分方程組的解,論證了其解析解與一個代數(shù)方程等價,證明了此方程經(jīng)變換后可用標準牛頓方法計算。考慮聲速的作用,建立了發(fā)射、接收點分開的主動聲納探測模型,構(gòu)造了基于距離、方位觀測值解算魚雷運動要素的相對較優(yōu)的彈道擬合準則。實現(xiàn)了小樣本條件下理想聲自導彈道估計的快速計算。仿真實驗證實,該方法預測的彈道可滿足反魚雷魚雷射擊參數(shù)計算的需要。
聲自導魚雷;運動要素解算;彈道擬合準則;反魚雷魚雷
水面艦船以反魚雷魚雷對抗?jié)撋漪~雷之前,需要計算預先設(shè)計的反魚雷魚雷射擊參數(shù)[1-3],其依據(jù)是水面艦船確認魚雷報警后對魚雷的觀測。這些觀測一般以主動聲納方式進行,可以給出魚雷的距離與方位等信息。在一定的條件下,利用這些信息可以對魚雷的彈道進行估計。基于魚雷彈道過程,相關(guān)條件可以假設(shè)為:魚雷處于直航、聲自導、線導等運動狀態(tài),對魚雷彈道的估計除當前時刻之前運動狀態(tài)的估計外,更主要的是對當前時刻之后運動狀態(tài)的預測[4-5]。
對應(yīng)于直航情形,魚雷運動狀態(tài)可以用當前時刻位置、航速、航向這幾個運動要素表達。在有距離、方位等觀測信息的條件下,估計魚雷彈道狀態(tài)比較簡單,這里所說的簡單主要是模型簡單、算法簡單、計算速度快、精度高等。對應(yīng)于聲自導情形,這類問題將變得復雜,作者未發(fā)現(xiàn)相關(guān)報導。
聲自導運動方式主要有被動、主動、主被動聯(lián)合等,一般由變周期的分周期控制實現(xiàn),控制的規(guī)則有固定提前角、變提前角等。若固定提前角為零,即直瞄式或尾追式跟蹤,這是魚雷被動聲自導運動的主要制導方式,這時,考慮到制導周期很小,可以近似認為魚雷速度方向總是魚雷到本艦(噪聲源)的方向,以下稱之為理想聲自導運動,本文只就這一情形進行相關(guān)問題的研究。研究主要包括理想聲自導魚雷運動狀態(tài)的計算、無誤差條件下主動聲納對魚雷的距離方位觀測值的計算、考慮誤差條件下理想聲自導魚雷運動要素估計等。
1 理想聲自導彈道狀態(tài)及計算
假設(shè)水面艦船以速度v等速直航,魚雷以速度vT對水面艦船進行理想聲自導跟蹤,速度方向為魚雷到水面艦船噪聲源的方向。以水面艦船艦艉(假設(shè)為噪聲源)作為其位置參考點,對魚雷進行觀測的某個時刻為零時刻,假設(shè)零時刻魚雷已經(jīng)處于理想聲自導運動狀態(tài)。由于魚雷聲自導運動的空間范圍較小,可以忽略地球橢球形狀的影響,將水面艦船的運動看成零時刻所處水平面上的運動。魚雷對水面艦船的跟蹤分為水平面上的跟蹤與豎直面上的跟蹤,尾追階段基本上已處于戰(zhàn)斗深度,可以忽略其變深運動。假設(shè)只進行水平面上的跟蹤,則運動規(guī)律與其在水面上的投影點的運動規(guī)律相同。因此,以零時刻水面艦船位置點為原點,在當?shù)厮矫嫔?以水面艦船速度方向為x軸正方向,其正右方向為y軸正方向,建立一個該水平面上的直角坐標系,以描述水面艦船及魚雷的運動。為便于公式推導,平面直角坐標系的點(x,y)以及原點到這點的自由向量以復數(shù)x+iy表示,i為虛數(shù)單位。
如圖1,在上述坐標系下,水面艦船總是位于實軸Ox軸上,時刻t到原點的距離為vt,所以表示水面艦船位置點Ov(t)的位置向量OOv(t)復數(shù)為實數(shù)vt,即
Ov(t)=vt
(1)
假設(shè)魚雷運動狀態(tài)以t時刻相對水面艦船的距離D(t)、舷角X(t)表示,則其絕對位置點G(t)的復數(shù)為
G(t)=vt+D(t)eiX(t)
(2)
式中:i為虛數(shù)單位。
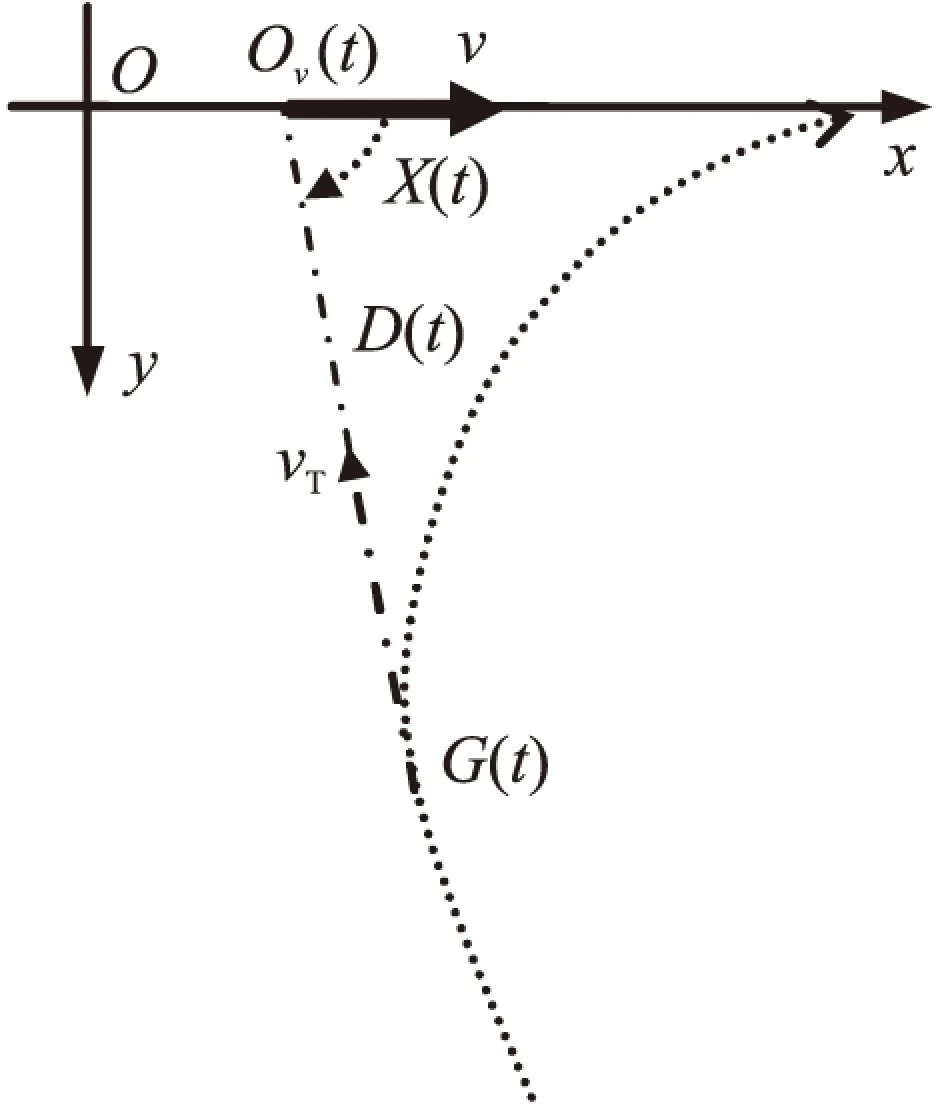
圖1 理想聲自導運動
1.1魚雷運動狀態(tài)的微分方程組
魚雷運動的速度向量復數(shù)為
G′(t)=v+[D′(t)+D(t)iX′(t)]eiX(t)
(3)
式中:G′(t),D′(t),X′(t)表示這些時間變量函數(shù)的導數(shù)。
由前面關(guān)于理想聲自導的假設(shè),魚雷速度方向相對Ox軸的角為X(t)+π,所以其速度向量復數(shù)的另一表示為vTei(X(t)+π),將這一表示與G′(t)相等,則
-vT=ve-iX(t)+D′(t)+D(t)iX′(t)
(4)
改成實部與虛部表示的分量形式:
(5)
此即魚雷相對水面艦船運動狀態(tài)所滿足的微分方程組。給定任一時刻t0的距離D(t0),舷角X(t0),總有唯一解,(D(t),X(t)),t≥0,因此(D(t0),X(t0))可以作為理想聲自導魚雷的運動要素。運動狀態(tài)的計算就是解這個微分方程組,在解算魚雷運動要素的搜索算法中要不斷調(diào)用解這個方程組的計算程序。若用數(shù)值方法計算,一方面計算誤差隨著時間變長而增加,更主要的是計算速度遠不能滿足需要。因此,必須尋找解微分方程組(5)的精確快速算法。
考慮到對稱性,只研究0≤X(t)≤π的情形。若X(t0)=0(或π),即自水面艦船正前方(或正后)方跟蹤目標,魚雷將作直線運動,且舷角保持X(t)=X(t0),D(t)=D(t0)-(v+vT)(t-t0)(正前方),或D(t)=D(t0)-(v-vT)(t-t0)(正后方),自t0時刻至魚雷追上水面艦船時刻的跟蹤時間tg=D0/(v+vT)(正前方),或tg=D0/(v-vT)(正后方)。下面假設(shè)t0>0,D(t0)>0,0 (1/D)dD/dX=-kcscX-cotX (6) 式中:k=vT/v,此方程有解析解: D=D(t0)sinX(t0)tank[X(t0)/2]cotk(X/2)cscX (7) 只要能計算X(t),就可以用此式計算D(t)。因為式(6)正比于cosk-1(X/2)/sink+1(X/2),所以,D→0?k>1,X→π,即當且僅當魚雷速度大于水面艦船速度,理想聲自導運動的魚雷才能追上目標,且總是自正后方追上目標,以下假設(shè)k>1。 將式(7)代入式(5)可得X(t)的微分方程: csc2X(t)cotk[X(t)/2]X′(t)=r (8) 式中: r=[v/D(t0)]cscX(t0)cotk[X(t0)/2] (9) 式(8)兩邊自t0到t積分,得: (10) 此為X(t)所滿足的方程,計算魚雷彈道狀態(tài)的關(guān)鍵就是解這個方程。式(10)中的時間滿足-t0≤t-t0≤tg,tg為跟蹤時間,只需在式(10)令t→t0+tg,X(t)→π,即可得: (11) 式(11)即為計算理想聲自導跟蹤時間的公式,對X(t0)=0(或π)的情形同樣成立。 1.2魚雷彈道狀態(tài)的計算 前文已將微分方程組(5)的求解變?yōu)橐粋€關(guān)于未知數(shù)X(t)的代數(shù)方程(10)的求解,雖然這個方程無解析解,但可以用比較標準的方法精確快速地計算。 利用r,tg的表達式可將式(10)改為 (12) 令z=cot[X(t)/2]∈(0,∞),則 X(t)=2arccotz 方程(12)變?yōu)?/p> (13) 因為g′(z)=zk-2+zk>0,所以g(z)為(0,∞)上單調(diào)上升函數(shù)。因為g(0)<0,g(∞)=∞,所以g(z)=0在(0,∞)上有唯一解。 用Newton方法計算一元方程的數(shù)值解十分快速和精確,對于單調(diào)上升(下降)的函數(shù),只要其二階導數(shù)大于(小于)0,起點的選擇可不作要求。對于函數(shù)g(z),考慮到g″(z)=(k-2)zk-3+kzk-1,若k≥2,則g″(z)>0,無論方程的解小于z0(t0 定理1設(shè)b>a>0,函數(shù)y=g(z)在[a,b]上有二階連續(xù)導數(shù),且g′(z)>0,z ∈[a,b],則存在α>0,使f(u)=g(uα),滿足f′(u)>0,f″(u)>0,u∈[a1/α,b1/α]的充要條件為p=minz∈[a,b]zg″(z)/g′(z)>-1,且可取α=1/(1+q),q∈(-1,p]。 證明?α>0,u∈[a1/α,b1/α] f′(u)=g′(uα)αuα-1>0 f″(u)=g″(uα)(αuα-1)2+g′(uα)α(α-1)uα-2? f′(u)>0,f″(u)≥0,?u∈[a1/α,b1/α]? f″(u)≥0,?u∈[a1/α,b1/α]? uαg″(uα)/g′(uα)+1-1/α≥0,u∈[a1/α,b1/α]? 0<1/α≤1+zg″(z)/g′(z),z∈[a,b]? p=minz∈[a,b]zg″(z)/g′(z)>-1 且 α≥1/(1+q),q ∈(-1,p] 證畢。 式(13)的g(z)滿足: g′(z)>0,0 取α=1/(1+k-2)=1/(k-1),則 滿足: f′(u)>0,f″(u)≥0,u∈[0,u0],u0=z0k-1 可以用u0為起點的Newton方法計算方程f(u)=0的數(shù)值解u*,迭代格式為 ul+1=ul-f(ul)/ f′(ul),l=0,1,… (14) 停止條件為l>lmax或|f(ul)|<ε,實驗程序內(nèi)取lmax=5,ε=10-15,實際計算時取uα=eαlnu,還能提高計算速度。圖2是k<2的一次實驗對應(yīng)的g(z),f(u)的圖形,圖中,u,f(u),z,g(z)均為無量綱量。 g(z)=0的數(shù)值解為z*=(u*)α,以此可以計算t≤t0+tg時刻的X(t),D(t),之后以式(2)計算魚雷絕對位置點復數(shù),以公式: vG(t)=-vTeiX(t) (15) 計算魚雷速度向量復數(shù)。 圖2 k=1.2113時g(z),f(u)曲線 設(shè)水面艦船以主動聲納探測魚雷,信號發(fā)射點P(t)相對艦艉的有向線段數(shù)量為Ls,信號接收點Q(t)相對艦艉的有向線段的數(shù)量為Lr,則其對應(yīng)的復數(shù)為 P(t)=vt+Ls, Q(t)=vt+Lr (16) Ls或Lr的符號為正表示相應(yīng)的點位于艦艉前方,符號為負表示相應(yīng)的點位于艦艉后方,為簡單起見,假設(shè)這些點與魚雷位于同一水平面上。記主動信號發(fā)射時刻為ts,j,j=1,2,…,ts,j時刻由P(ts,j)點發(fā)射的信號到達魚雷的時刻記為tr,j,假設(shè)到達信號在G(tr,j)點被魚雷立即反射,反射信號到達接收點的時刻記為ta,j。假設(shè)聲波在水中的傳播可近似為直線,平均聲速為常數(shù),記為vs,則 |G(tr,j)-P(ts,j)|=vs(tr,j-ts,j) (17) |Q(ta,j)-G(tr,j)|=vs(ta,j-tr,j) (18) 給定j,z=tr,j-ts,j,由式(17)有: (19) 其解z*可利用Newton方法計算,格式同式(14),起點可取1.5|G(ts,j)-P(ts,j)|/vs,方程(19)左端函數(shù)的導數(shù)計算公式為 ta,j為方程(18)的解,可以用上述方法計算。但由于接收點Q(t)等速直航,與方程(17)不同,故方程(18)為一個關(guān)于δ=ta,j-tr,j的二次方程,因此有簡單的解析計算公式。 定理2以A(t),B(t)表示2個水下運動物體t時刻位置點的空間坐標,記w=-1(A發(fā)B收),1(B發(fā)A收),設(shè)B以速度vB=(vBxvByvBz)勻速運動,‖vB‖ 式中:U=A(tA)-B(tA),q=U(vB/ vs) 證明由已知: ‖A(tA)-B(tB)‖=vs(tA-tB)w 因為B(t)=B(0)+vBt,所以 B(tB)=B(tA)-vB(tA-tB) ‖U‖2+2(UvB)(tA-tB)+‖vB‖2(tA-tB)2 用求根公式計算tA-tB,因為‖vB/vs‖<1,根式前面的正負號與w相同。證畢。 利用上述定理可得: (20) 式中:Uj=G(tr,j)-Q(tr,j),q=ksReUj,ks=v/vs。 接收點于ta,j時刻收到信號的理論距離及到達方位(此處以舷角表示)為 d0j=|G(tr,j)-Q(ta,j)| (21) β0j=arg[G(tr,j)-Q(ta,j)] (22) 假設(shè)無系統(tǒng)誤差,只考慮隨機觀測誤差,這些理論值的觀測值為 dj=d0j+Δdj (23) βj=β0j+Δβj (24) 為簡單起見,假設(shè)這些觀測值都在可觀測范圍內(nèi),Δdj,Δβj,j=1,2,…,相互獨立,且 所謂距離方位觀測解算,就是用當前時刻t0之前(ta,j 即可以只用觀測值dj,j=1,…,n,求出(D(t0),X(t0))的極大似然估計,且這個估計與以Jd為目標函數(shù)的最小二乘法估計相同。 同樣也可以只用βj,j=1,…,n,給出(D(t0),X(t0))的極大似然估計,且與以 為目標函數(shù)的最小二乘法估計相同。 為便于反魚雷魚雷發(fā)現(xiàn)魚雷以及發(fā)現(xiàn)魚雷時刻的態(tài)勢有利于后續(xù)的跟蹤,只要有可能,就應(yīng)利用所有觀測信息對魚雷運動狀態(tài)給出精確的預測[6]。因此必須綜合考慮樣本(dj,βj),j=1,…,n,其似然函數(shù)為 對于σd,σβ已知的情形,這對應(yīng)于以 為目標函數(shù)的加權(quán)最小二乘法估計,對于σd,σβ未知的情形,Jd,β不能作為目標函數(shù),只能以L為目標函數(shù)求(D(t0),X(t0))的極大似然估計,這其中包含對σd,σβ的估計。 數(shù)值實驗發(fā)現(xiàn),搜索以上這幾種目標函數(shù)的最優(yōu)點需要較長的時間,且對于樣本容量n 較小的情形,估計的精度不足。為此,考慮一種彈道擬合的方法,記 zj=djexp(iβj), j=1,…,n (25) 為ta,j時刻魚雷相對于接收點的觀測位置復數(shù),則復隨機變量zj的數(shù)學期望E(zj)為 E(zj)=E[(d0j+Δdj)exp(i(β0j+Δβj))]= E(d0j+Δdj)E[exp(i(β0j+Δβj))]= d0jexp(iβ0j)E[exp(iΔβj)] 由正態(tài)分布特征函數(shù)在點1處的值可知: (26) 所以 (27) 因為 |zj-E(zj)|2=|(d0j+Δdj)exp[i(β0j+Δβj)]- 所以zj的方差Var(zj)為 (28) 式(27)、式(28)說明距離方位觀測條件下,觀測位置點并非理論位置點的無偏估計,且是異方差的,為平衡各次觀測,可令 (29) 為目標函數(shù),以 minJ(D(t0),X(t0)) s.t. (D(t0),X(t0))∈(0,dmax)×(0,π) 的解D*(t0),X*(t0)作為D(t0),X(t0)的估計,此處稱之為彈道擬合準則。數(shù)值實驗發(fā)現(xiàn),這個最優(yōu)問題的求解速度較其他方法快,且以最近的15~25個觀測樣本,能給出滿足射擊參數(shù)計算等要求的彈道估計。圖3為一次計算的圖形(輸入?yún)?shù),略)。 圖3 一次仿真實驗預測的魚雷彈道 本文構(gòu)造了對理想聲自導運動的魚雷運動要素進行基于距離方位觀測的估計方法,用仿真實驗進行了驗證。該方法對于解算等速直航運動或其他參數(shù)化彈道的魚雷運動要素同樣適用。但這類方法的 實質(zhì)為非線性最優(yōu)化問題,其算法的速度一般不能滿足實時計算的需要,對于給定的算法速度,必須設(shè)置發(fā)射反魚雷魚雷的時刻較當前時刻t0有一點延遲,給計算預留一定的時間。正是這一原因,需要嘗試一些提高算法速度的辦法。 [1]李本昌,李長文.預定相遇態(tài)勢的潛射魚雷射擊及其技術(shù)方法[J].指揮控制與仿真,2013,35(2):5-8. LI Ben-chang LI Chang-wen.Firing and technical method based on given meeting situation of sub-launched torpedo[J].Command Control & Simulation,2013 35(2):5-8.(in Chinese) [2]李長文,李本昌,初磊.預定相遇態(tài)勢的魚雷二次轉(zhuǎn)角射擊通用模型與算法[J].魚雷技術(shù),2013,21(4):306-312. LI Chang-wen,LI Ben-chang,CHU Lei.General model and algorithm of two-time turn angle shooting of torpedo for predetermined encountering situation[J].Torpedo Technology,2013,21(4):306-312.(in Chinese) [3]由大德,徐德民.反魚雷魚雷攔截概率影響因素仿真分析[J].魚雷技術(shù),2010,18(4):312-315. YOU Da-de,XU De-min.Analysis on parameters influencing intercept probability of anti-torpedo torpedo[J].Torpedo Technology[J],2010,18(4):312-315.(in Chinese) [4]陳顏輝,朱偉良,杜毅.潛射魚雷彈道預測模型與仿真[J].海軍工程大學學報,2013,25(2):57-61. CHEN Yan-hui,ZHU Wei-liang,DU Yi.Trajectory prediction model and simulation of sub-launched torpedo[J].Journal of Naval University of Engineering,2013,25(2):57-61.(in Chinese) [5]姜凱峰,周明,林宗祥.艦載反魚雷魚雷作戰(zhàn)效率仿真研究[J].計算機仿真,2011,28(6):9-12. JIANG Kai-feng,ZHOU Ming,LIN Zong-xiang.Operational efficiency based on simulation of shipboard anti-torpedo torpedo[J].Computer Simulation,2011,28(6):9-12.(in Chinese) [6]李宗吉,張西勇,練永慶.反魚雷魚雷自適應(yīng)滑模導引律[J].彈道學報,2015,27(1):24-26. LI Zong-ji,ZHANG Xi-yong,LIAN Yong-qing.Antit-orpedo-torpedo adaptive sliding mode guidance[J].Journal of Ballistics,2015,27(1):24-26.(in Chinese) Method of Solving Motion Factors of Ideal Acoustic Homing Torpedo by Distance and Bearing Observations LI Chang-wen,CHU Lei (Navy Submarine Academy,Qingdao 266199,China) To predict the trajectory of acoustic homing torpedo fastly,the distance and bearing relative to this ship for specified time were taken as the torpedo motion factors,and the trajectory was parameterized to the solution of differential equations taking the factors as initial value.The result demonstrates that the analytic solution is equivalent to an algebraic equation,and this transformed algebraic-equation can be calculated using standard Newton method.A detection model of active sonar with the separation of sending and receiving point was established by considering sound speed influence.Based on the observation value of distance and azimuth,a relatively superior criterion named trajectory fitting for solving the motion factor was constructed.The fast calculation was realized for estimating the ideal acoustic homing trajectory under the conditions of small samples.Simulation results show that the torpedo trajectory predicted by this method can meet the parameters calculation for firing anti-torpedo torpedo. acoustic homing torpedo;solution to motion factor;trajectory fitting criterion;anti-torpedo torpedo 2016-01-25 李長文(1962- ),男,副教授,研究方向為隨機數(shù)學及軍事運籌學。E-mail:lcwqtxy2996@sina.com。 O315 A 1004-499X(2016)03-0043-05
2 主動聲納對理想聲自導魚雷的觀測

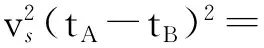
3 理想聲自導運動要素的距離方位觀測估計
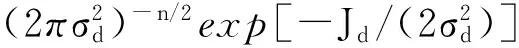

4 結(jié)束語

