ZPW-2000A型無絕緣移頻軌道電路補償方案研究

薛紅巖

(中鐵第一勘察設計院集團有限公司，西安　710043)

?

ZPW-2000A型無絕緣移頻軌道電路補償方案研究

薛紅巖

(中鐵第一勘察設計院集團有限公司，西安710043)

在現場的應用中，ZPW-2000A型無絕緣移頻軌道電路在安全性和可靠性方面有著顯著優勢，但其分路特性的改善是需要關注的問題。采用電平衰耗法的計算方法，對無補償電容、有補償電容和有最佳補償電容時的無絕緣軌道電路的分路特性進行分析，并用Matlab軟件仿真得到軌面各點的分路靈敏度和分路殘壓比較結果。結果表明，補償電容對軌道電路的分路特性有明顯的改善作用，而找到最佳補償電容值對軌道電路進行補償，不但能同時保證軌道電路全程可靠分路，并且降低了分路殘壓，使得無絕緣軌道電路的分路特性更穩定。

無絕緣軌道電路；補償電容；分路特性；分路靈敏度

1　概述

ZPW-2000A型無絕緣軌道電路具有較高安全性，自2003年至今，在全路得到了全面運用，技術成熟。由于裝設無絕緣軌道電路不切割鋼軌，面對越來越高的列車運行速度，無絕緣成為軌道電路必須具備的條件，這是各國紛紛采用無絕緣軌道電路的主要原因。無絕緣移頻軌道電路雖然在目前應用廣泛，但也并不是盡善盡美的，根據現場使用的情況，仍需對其做進一步的優化和改進，才能適應快速發展的高速鐵路的要求。其中補償電容的設置對無絕緣軌道電路的傳輸特性和分路特性的提高起到了非常大的作用，但現階段的工程設計和實際應用中，對無絕緣軌道電路補償電容的容值的大小都是固定在某幾個值上[1]，這其實限制了補償的作用，在某些特殊惡劣條件下，并沒有達到最佳的補償效果。本文通過對不加補償電容、加裝補償電容的現有方式對ZPW-2000A型無絕緣軌道電路分路特性影響的分析，提出尋求軌道電路的最佳補償方案的方法，并結合工程實際，驗證其可行性。

2　無絕緣軌道電路分路狀態現狀的分析

2.1不加補償電容時軌道電路分路靈敏度的計算

分路狀態最不利條件下(道床電阻為無窮大時)，在沒有加補償電容時，ZPW-2000A型無絕緣軌道電路的等效電路如圖1所示[2，3]。

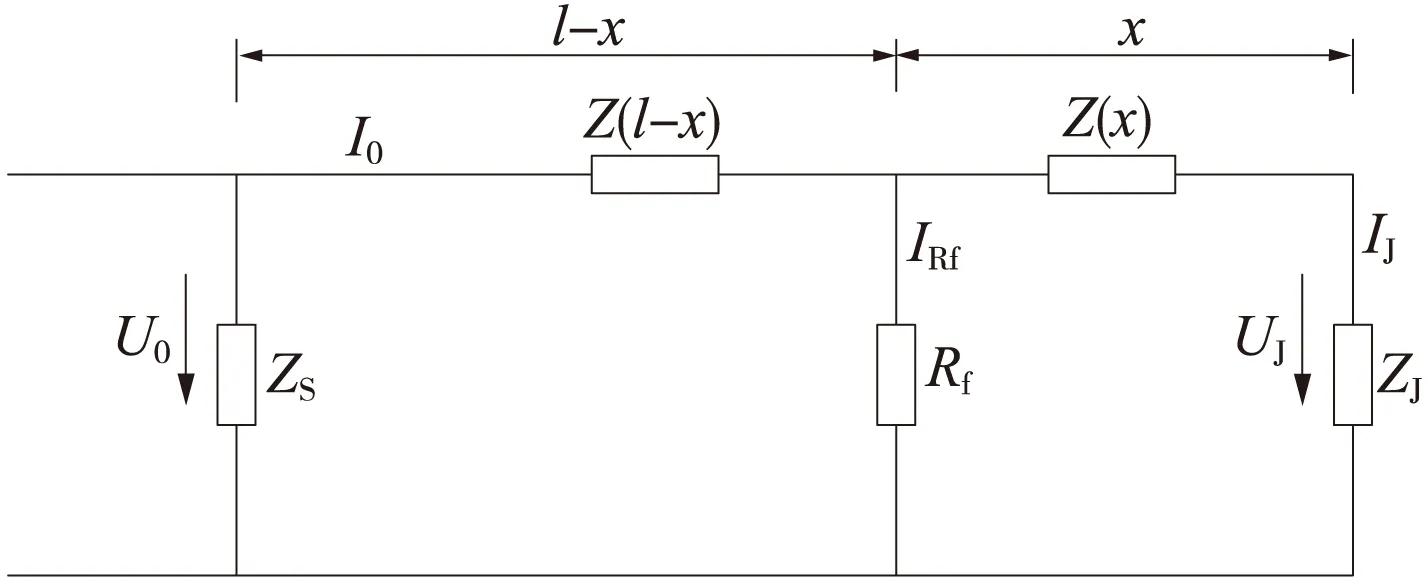
圖1　無補償電容時軌道電路的等效電路

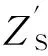
列車在軌面任意點分路時，軌道電路衰耗為

(1)

式中，P0為發送設備向電氣絕緣節調諧單元的右側軌道輸入的功率；PJ為接收設備輸出給電氣絕緣節調諧單元和負載的功率。

根據圖1所示的軌道電路等效電路圖，用接收端的電壓UJ、電流IJ表示發送端的輸入電壓U0、電流

(2)

(3)

當列車在軌道電路終端(接收端)分路時，x=0，這時的軌道電路衰耗為

(4)

將式(2)、式(3)代入式(4)中，可得

b0=4.343×

(5)

當列車在始端(發送端)分路時，x=l，這時的軌道電路衰耗為

(6))

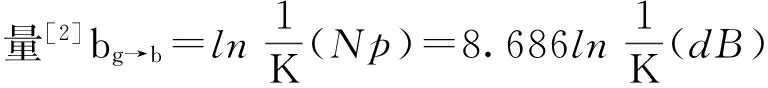
(7))

式中，K為接收器的返還系數。所以，列車在軌道電路終端和始端可靠分路必須滿足衰耗條件式(8)或式

(8)

(9)

式中，bmax為軌道電路允許的最大衰耗量。由于極限分路靈敏度在軌道電路的兩端[4]，所以無補償軌道電路的極限分路靈敏度必然在始端或終端，將式(8)、式(9)兩個不等式取等號，使其變為等式，再用數值迭代法即可求得發送端和接收端的的分路靈敏度。

由此推理出，在軌道電路任意點分路必須滿足的條件是

(10)

假設在頻率為1 700 Hz、軌道長度1.5 km時，軌面各點的分路靈敏度通過上述計算得到如圖2所示的曲線。

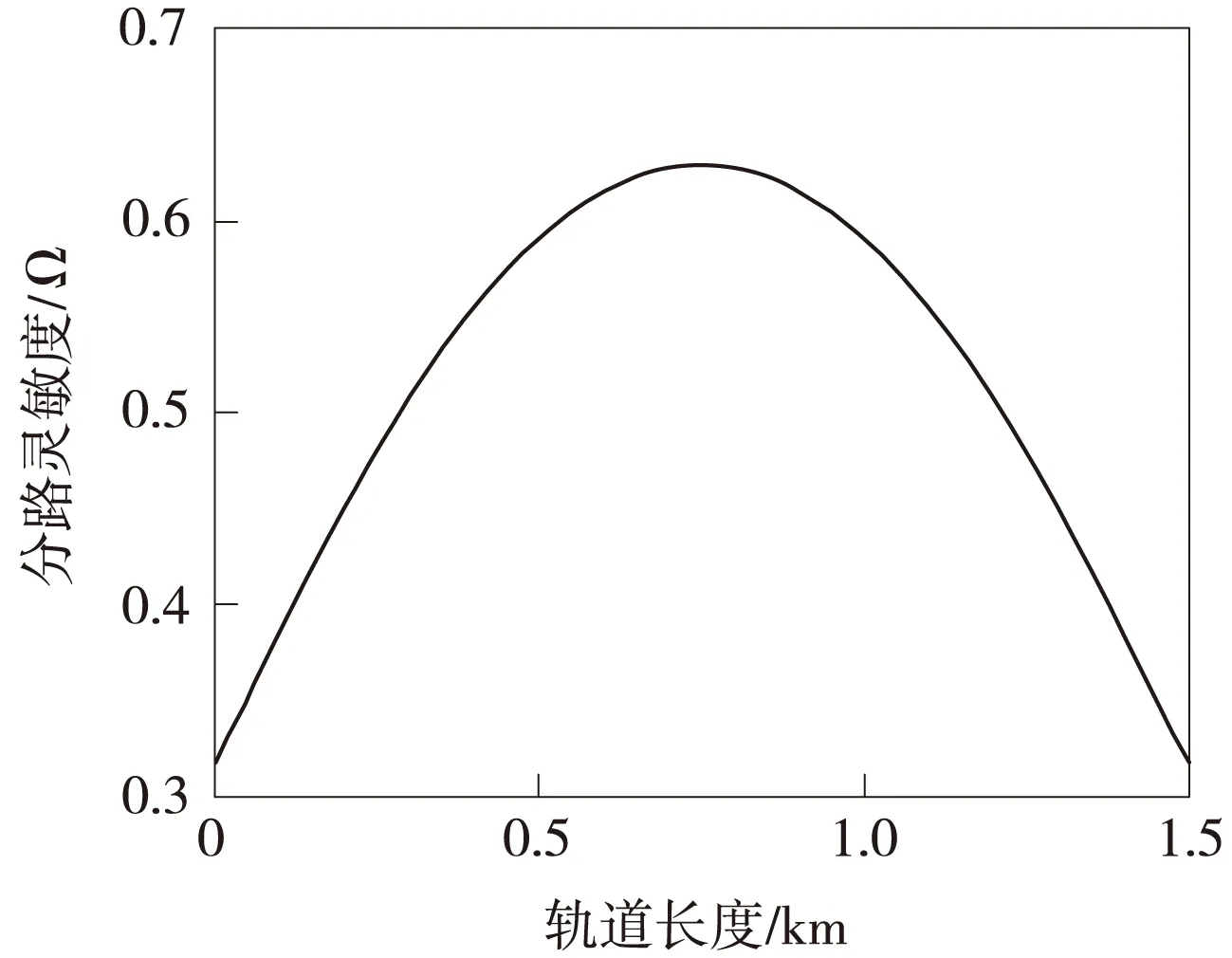
圖2　無補償電容時軌面各點的分路靈敏度

圖2中坐標原點為軌道電路終端。從圖2可以看出，無絕緣軌道電路在無補償的情況下，最難分路的地方在兩端，而有較好分路特性的地方在中間，也就是說，不設補償電容的軌道電路的長度只能在中間分路性能較好的范圍內取值，且軌面各點分路的難易程度相差較大，不利于調整。

2.2加裝補償電容時軌道電路分路靈敏度的計算

在有補償電容的無絕緣軌道電路分路特性的分析中，很難定量計算出其軌面各點的分路靈敏度大小，而采用電平衰耗的方法對其分路狀態分析較為簡便[5，6]。

有補償電容時，終端分路的軌道電路等效電路如圖3所示。

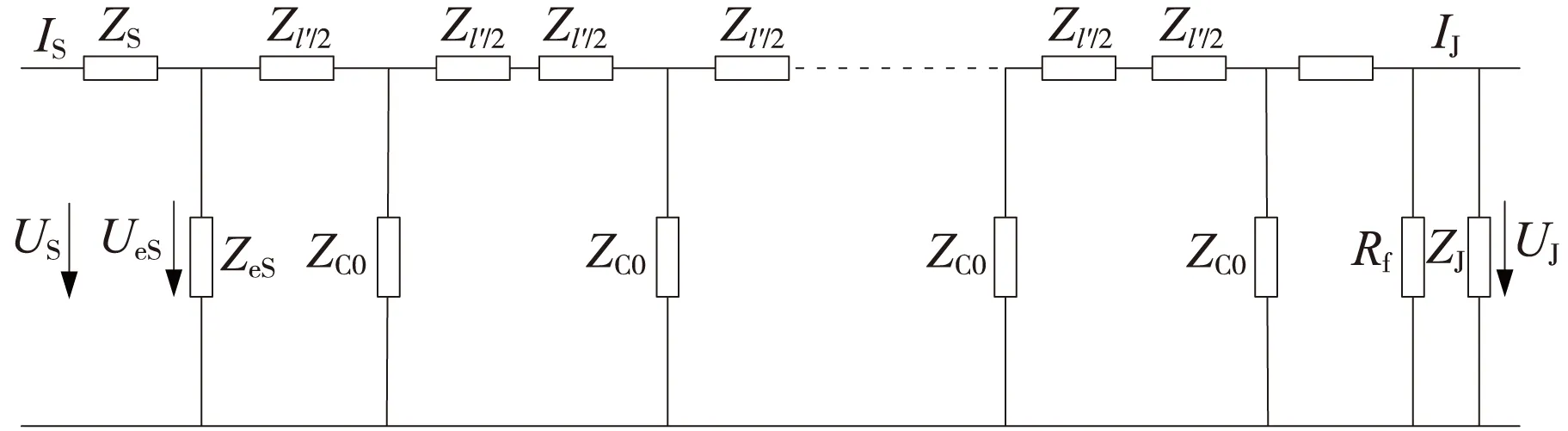
圖3　終端分路時軌道電路等效電路

有補償電容時，始端分路的軌道電路等效電路如圖4所示。

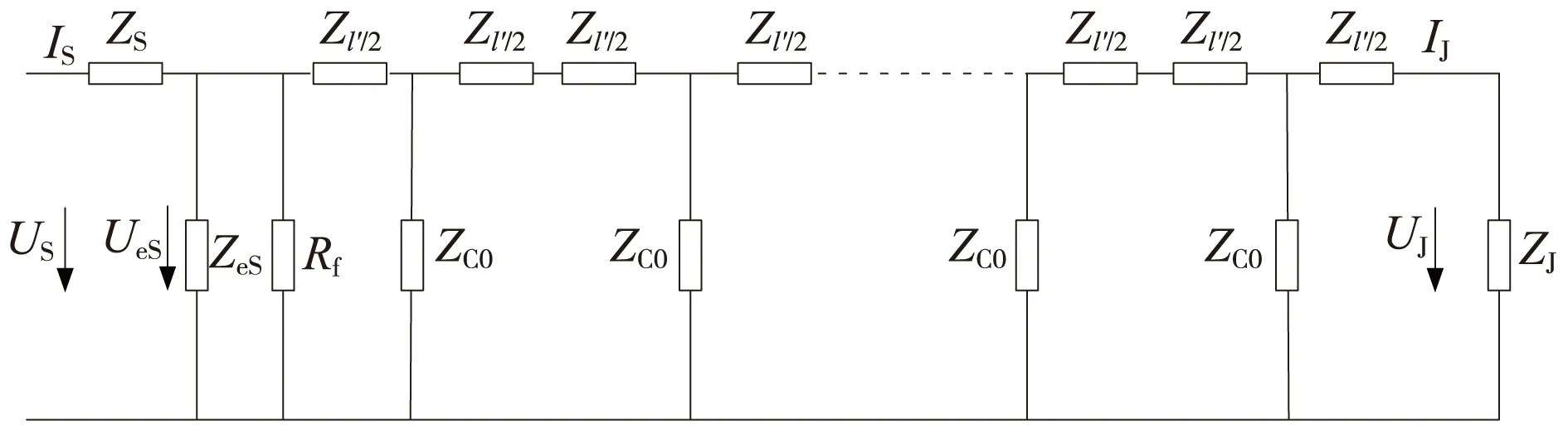
圖4　始端分路時軌道電路等效電路

要得到其分路衰耗，先要計算一個補償節的T型等效電路的衰耗。補償節T型等效電路如圖5所示。

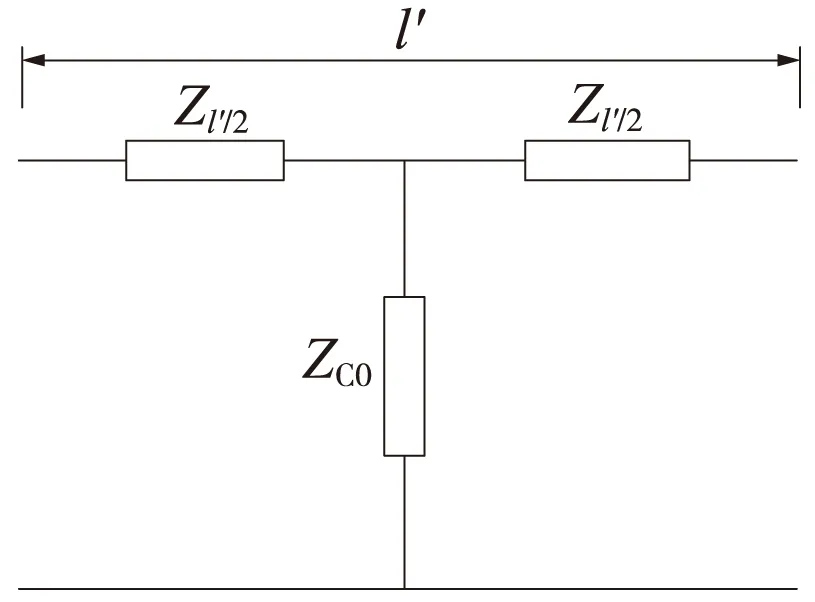
圖5　T型等效電路

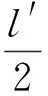
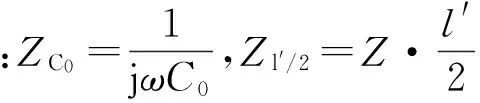
圖5所示的T型等效電路的四端網系數為

(11)

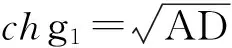
(12)

(13)

(14)

(15)

(16)

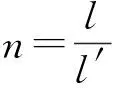
(17)

此四端網的特性阻抗記作ZT，ZT與四端網A參數之間的關系

(18)

列車在軌道電路上分路所引起的衰耗主要有兩種[2]：一種是分路衰耗，另一種是失配衰耗。

終端分路衰耗

(19)

終端與鋼軌的失配衰耗

(20)

始端分路衰耗

(21)

式中，UeS為ZeS的端電壓。

始端與鋼軌失配衰耗

(22)

要使接收端可靠分路，必須滿足衰耗條件[2]

(23)

發送端可靠分路，必須滿足的衰耗條件是[2]

(24)

同樣將上述兩式的大于等于號取等號，再用數值迭代法即可求得發送端和接收端的的分路靈敏度。

加了補償電容后，極限分路靈敏度的位置很難確定，所以不便用分路靈敏度的方法來表征其整個軌道電路的分路特性，而采用ZPW-2000A的標準分路電阻(0.15 Ω)對軌道電路任意點分路時的分路殘壓來表征其分路性能。

在隴海線天蘭段天水至南河川區間下行14019G區段，頻率為1 700 Hz、軌道長度1.3 km， 同等條件下對無補償情況和有補償情況的全程分路殘壓比較如圖6所示。

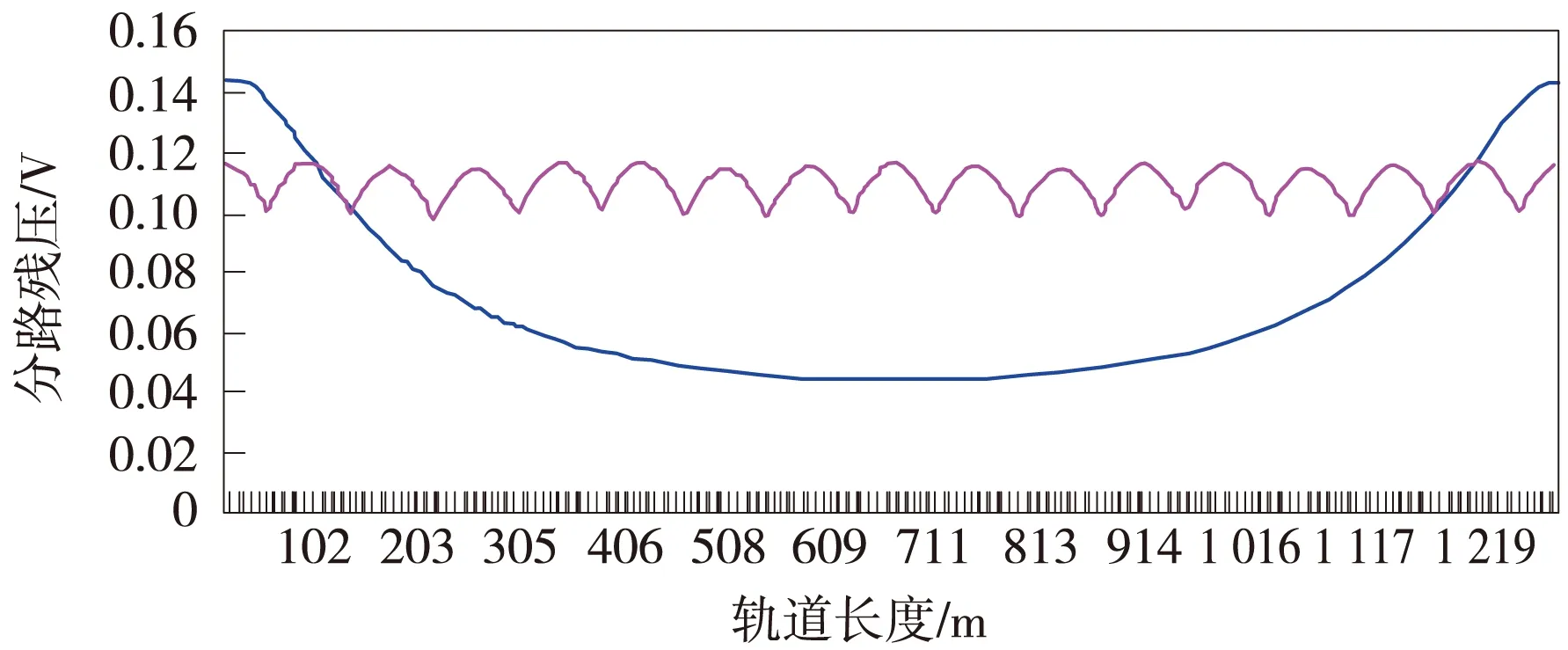
圖6　隴海線天水之南河川區間14019G有補償和無補償軌道電路全程的分路殘壓比較

圖6中坐標原點為軌道電路始端；橫坐標為軌道長度(m)，縱坐標為分路殘壓(V)；向下凹的光滑曲線為無補償的分路殘壓，波浪線為有補償的分路殘壓。從分路殘壓的角度可以看出，補償電容對軌道電路整體的分路靈敏度有很大的提高，但是補償電容的加入打亂了原本軌道電路軌面各點分路靈敏度有規律的排列，使得軌面上各點的分路靈敏度情況復雜化。

3　最佳補償方案的研究

為了穩定軌道電路在不同地點的分路靈敏度，尋求最佳的補償效果，圖7中繪出了頻率為1 700、2 000、2 300、2 600 Hz時，軌道區段均勻補償時的最佳補償電容值與道床電阻的關系曲線。

從圖7可以看出：在同頻的軌道區段內最佳補償電容值隨著道床電阻的增大而減小；在不同頻的軌道區段內最佳補償電容值隨著信號頻率的增大而減小。當軌道區段的信號頻率一定的時候，鋼軌的阻抗值是一個固定值，集中補償方式的最佳補償電容值與道床電阻成反比；而當道床電阻值一定、不同軌道區段的信號頻率變化的時候，鋼軌的阻抗值會發生變化，鋼軌阻抗值隨著信號頻率的增大而增大，所以補償電容值隨信號頻率的增大而減小。

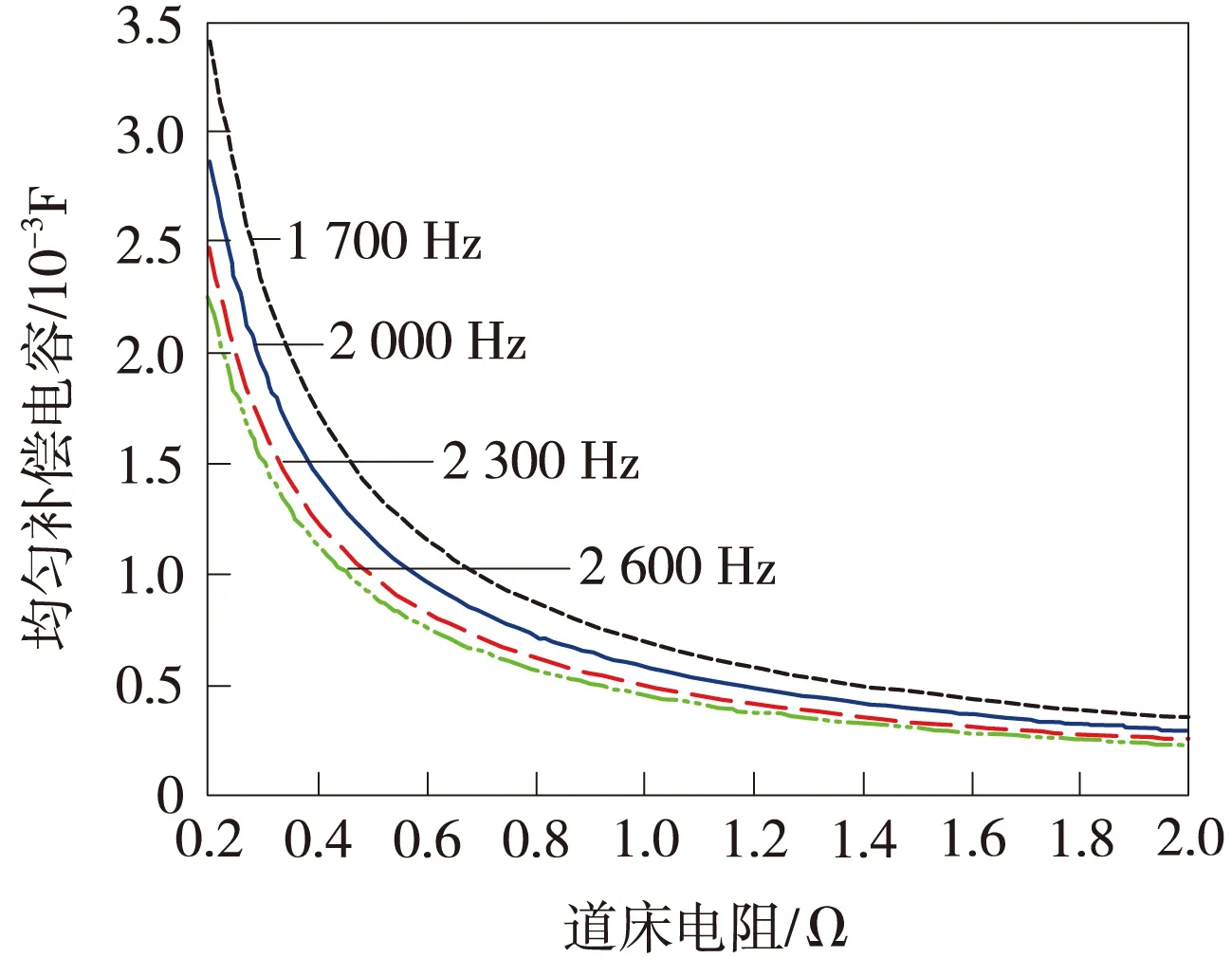
圖7　頻率不同的軌道電路中補償電容與道床電阻的關系

4　最佳補償電容值的確定

最佳補償電容值也就是使整個區段內的補償電容等效為一個連續的均勻分布的補償電容時的電容值[7，8]。確定最佳補償方式的補償電容值，也就是要使整個軌道電路的特性阻抗趨近于純阻性，并使傳輸衰耗最小[9]。最佳補償電容值也就是使等效的連續電容補償網絡的衰耗常數達到最小時的集中補償電容值，可以用數值迭代方法確定。

實際電容補償就是按照等間距設置補償電容[10，11]。電容集中補償的軌道電路的等效T型四端網絡如圖8所示。

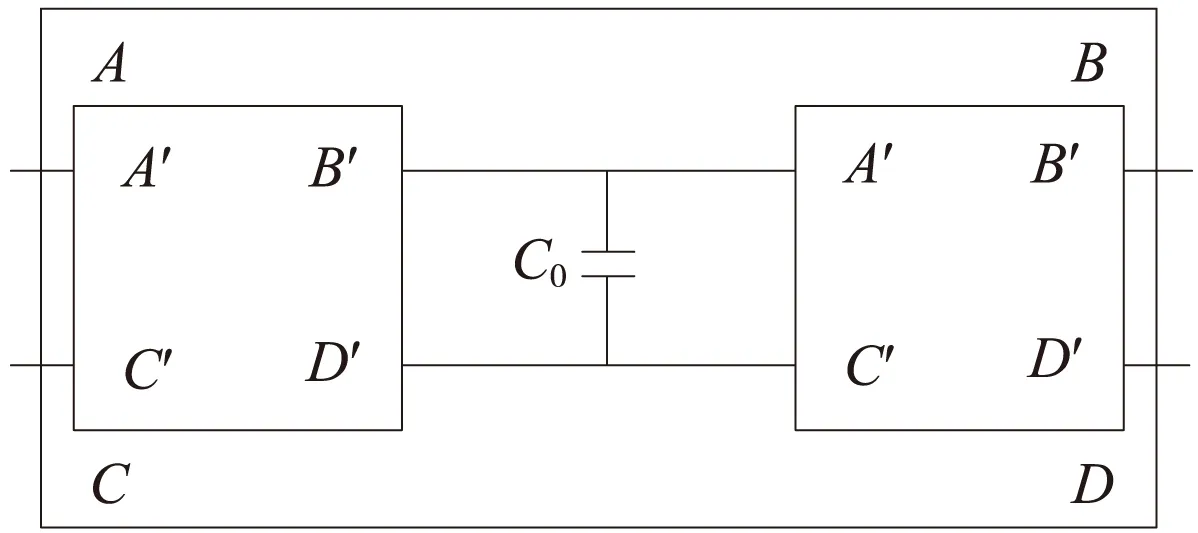
圖8　T型等效四端網絡

經過一系列矩陣變換，可以計算出包括補償電容C0在內的三個級聯的四端網合并而成的四端網絡的系數A、B、C、D

(25)

由此可以推出

(26)

理想的連續電容補償的軌道電路含有一個補償電容的T型等效網絡的衰耗常數由式(26)確定[12-13]。可以看出軌道電路的衰耗常數β′隨著g模值的增加而增加。所以，只要求出g的最小模值就求出了最小的衰耗常數[14-15]。

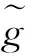
(27)

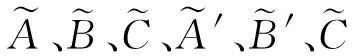
同樣以上述隴海線天蘭段天水至南河川區間下行14019G區段為例，頻率為1 700 Hz、軌道長度1.3 km。經過迭代運算得到：在1 700 Hz區段的最佳集中補償電容值為50.4 μF，即在軌道區段的每100 m處并聯1個50.4 μF的補償電容。同等條件下全程分路殘壓比較如圖9所示。

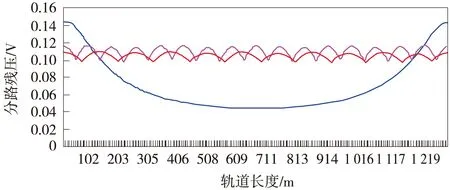
圖9　隴海線天水至南河川區間14019G最佳補償、實際補償和無補償軌道電路全程的分路殘壓比較

圖9中比圖6中多的較為光滑的波浪線為最佳補償的分路殘壓。可以看出，最佳補償電容比實際1 700 Hz區段中固定容值的補償電容更能提高軌道電路的分路靈敏度，且軌面各點的分路靈敏度雖仍有起伏，但已改善了很多。

5　結語

不加補償電容的無絕緣軌道電路，在分路的情況下，軌面各點的分路靈敏度分布曲線呈開口向下的拋物線，其極限分路靈敏度在軌道電路的始端或終端。而加了補償電容的無絕緣軌道電路分路時，軌面各點的分路靈敏度情況變得沒有規律，極限分路靈敏度的位置亦不確定。對于ZPW-2000A的無絕緣軌道電路來說，加了補償電容使得在任意點分路時的分路殘壓分布在一個較小的范圍內，降低了始、終端附近的分路殘壓，改善了分路狀態。而更精確地找到軌道電路的最佳補償電容值，不但能同時保證軌道電路全程可靠分路，并且降低了分路殘壓，較現有的集中補償電容值所得到的軌道電路全程分路殘壓曲線更優、分路性能更好。

本文是從等間距(100 m)設置補償電容的角度出發來研究其對ZPW-2000A型無絕緣軌道電路的分路特性的影響，下一步還應從調整補償電容的間距(或為不等間距)的角度進行研究，以便找到穩定軌道電路分路靈敏度的方法。

[1]陶啟滬.鐵道信號基礎設備及原理[M].北京:中國鐵道出版社，1992.

[2]費錫康.無絕緣軌道電路原理及分析[M].北京:中國鐵道出版社，1993.

[3]趙志，程蔭杭.無絕緣軌道電路死區段的計算方法[J].鐵道學報，2000，22(5):51-54.

[4]趙會兵，章宇舟，汪希時.電容補償軌道電路若干問題的研究[J].鐵道學報，1998，20(4):77-79.

[5]趙志.諧振式無緣軌道電路傳輸特性及仿真的研究[D].北京:北方交通大學，2000.

[6]趙志，程蔭杭.無絕緣軌道電路死區段的計算方法[J].鐵道學報，2000，22(5):51-54.

[7]張少平.UM71型無絕緣軌道電路的調試與開通[J].鐵道通信信號，1994，30(7):15-17.

[8]李燁，徐中偉.電氣化鐵路移頻自動閉塞信號傳輸仿真的研究及應用[J].鐵道學報，2003，25(6):66-70.

[9]陳志穎.高速鐵路隧道群地段信號維護技術及體制的完善和應用研究[J].鐵道標準設計，2015，59(2):110-113.

[10]袁彥.軌道電路的建模與仿真[D].成都:電子科技大學，2005.

[11]馬濤，米根鎖，齊東.基于灰色理論ZPW-2000A無絕緣軌道電路故障風險分析[J].鐵道標準設計，2013(4):115-118.

[12]董昱.區間信號與列車運行控制系統[M].北京:中國鐵道出版社，2008.

[13]賈晨子.軌道電路參數測量和調整的研究[D].北京:北京交通大學，2007.

[14]阿·米·布列也夫，尤·阿·克拉夫，阿·付·希師良柯夫.軌道電路分析與綜合[M].北京:中國鐵道出版社，1981.

[15]魯恩斌，李宏一.區間及站內軌道電路干擾問題的分析和處理[J].鐵道通信信號，2009，45(3):35-36.

Research on Compensation Capacitance Scheme of ZPW-2000A Non-insulated Track Circuit

XUE Hong-yan

(China Railway First Survey and Design Institute Group Co.， Ltd.， Xi’an 710043， China)

The field application shows the obvious advantages of ZPW-2000A non-insulated track circuit in security and reliability， but its shunt characteristic still needs to be improved. The shunt characteristics of the track circuit with and without compensation capacitor and with optimal compensation capacitor are analyzed and shunt sensitivity and shunt residual voltage of the track circuit at each track surface point are compared and simulated with MATLAB simulation software. The results show that the compensation capacitor improves remarkably the shunt characteristic of the track circuit and the best compensation capacitance can not only guarantee track circuit reliability but also reduce the shunt residual pressure， and make the shunt characteristic of the non-insulated track circuit more stable．

Non-insulated track circuit， Compensation capacitor; Shunt characteristics; Shunt sensitivity

2016-01-20；

2016-02-19

薛紅巖(1983—)，女，工程師，2009年畢業于蘭州交通大學交通信息工程及自動化專業，工學碩士，E-mail：xue_hy@163.com。

1004-2954(2016)08-0139-05

U284.2

ADOI:10.13238/j.issn.1004-2954.2016.08.029