控制方向未知分數階混沌系統的Nussbaum增益同步

吳梅，程繼紅，余名哲，張友安

（1.煙臺毓璜頂醫院消防監控室，山東煙臺264001；2.海軍航空工程學院a.科研部；b.控制工程系，山東煙臺264001；3.91526部隊，廣東湛江524064）

控制方向未知分數階混沌系統的Nussbaum增益同步

吳梅1，程繼紅2a，余名哲3，張友安2b

（1.煙臺毓璜頂醫院消防監控室，山東煙臺264001；2.海軍航空工程學院a.科研部；b.控制工程系，山東煙臺264001；3.91526部隊，廣東湛江524064）

文章將Nussbaum增益控制引入分數階混沌系統，解決了分數階混沌系統在存在控制方向未知情況下的同步控制問題。首先，選取了一類穩定的分數階積分滑模面。然后，結合整數階Nussbaum增益控制方法與滑模變結構控制理論，設計了一種Nussbaum增益同步控制器。最后，作為例子，實現了分數階Chen系統和分數階R?ssler系統在控制系數未知時的混沌同步控制，數值仿真驗證了文中方法的正確性和有效性。

分數階混沌系統；同步；Nussbaum增益控制；控制方向未知

控制方向未知也屬于一種不確定性。所謂控制方向，也就是控制增益的符號，在通常的控制設計中，一般是需要預先獲知的。但當控制方向不確定時，混沌系統的控制問題將變得非常困難，特別是當控制系數時變或緩變時，如果涉及到增益符號的改變，原本穩定的系統可能會因為控制方向的改變而失去穩定。一般涉及到控制方向未知的情況大多會運用到Nussbaum增益控制方法。自從Nussbaum提出Nussbaum增益控制概念以來，該方法在控制設計中已經得到廣泛應用。針對不同的系統和控制目標，設計者會將Nussbaum增益控制與其他不同的控制技術相結合來設計控制器，從而達到控制目的。

在混沌同步中引入Nussbaum增益控制，已有文獻進行了相應研究［1-2］，但研究對象仍然局限于整數階混沌系統。由于分數階非線性系統控制有其特殊性，與整數階系統相比有較大不同，因而在考慮控制方向不確定時，引入Nussbaum增益控制，進而解決分數階混沌系統的同步問題仍是一個全新的課題。增益限制也是控制設計要考慮的因素［3］。文獻［4］將Nussbaum增益控制方法引入到整數階混沌系統的同步控制。文獻［5］提出一種基于Nussbaum增益的自適應Backstepping控制策略，實現了控制方向未知的嚴反饋系統的穩定控制。王強德等人［6］應用Nussbaum增益技術和遞推方法，結合自適應控制，實現了一類控制方向未知和時變不確定性的本質非線性系統的跟蹤控制。劉露等人［7］結合魯棒鎮定技術和Nussbaum增益控制技術控制方向未知的非線性系統的全局魯棒輸出調節問題。A.Boulkrounet等人［8］針對不確定多變量系統存在未知執行器非線性項和未知控制方向問題，采用Nussbaum增益控制技術，設計了模糊自適應控制器。葛樹志等人［9］研究了一類控制方向未知的嚴反饋非線性離散時間系統的自適應控制問題，運用離散Nussbaum增益克服了控制方向變化引起的控制困難。但以上應用Nussbaum增益控制的相關文獻均沒有考慮分數階混沌系統的同步控制問題。另一方面，雖然考慮分數階混沌系統的同步控制問題的相關文獻比較多［10-14］，但這些文獻都沒有應用Nussbaum增益控制方法解決控制方向未知情況下分數階混沌系統的的同步控制問題。

本文進一步將Nussbaum增益控制方法引入分數階混沌系統的同步控制，解決了控制方向未知情況下分數階混沌系統的同步控制問題。為不使問題過于復雜，本文重點考慮控制方向未知問題，暫不考慮增益受限問題和其他不確定因素的影響。

1　基礎知識

定義1：［15］如果函數N（χ）滿足

那么函數N（χ）稱為Nussbaum-type函數。

引理1：［15］若是光滑的Nussbaum-type函數，q≥1是奇數，則Nq（χ）也是光滑的Nussbaum-type函數。

引理2：［15］設V（t）和χ（t）是定義在區間上的光滑函數，對于，V（t）≥0，N（χ）是適當且光滑的Nussbaum-type函數，如果下列不等式成立：

式（2）中：c0是適當的常數；c1＞0；g（t）是取值于未知閉區間的時變參數，則V（t）、χ（t）和必定在區間上有界。

2　問題描述和模型建立

考慮如下分數階混沌系統

式（3）為最一般的系統表達式，分數階混沌系統均可用此式表示。將系統式（3）作為驅動系統，構建帶控制輸入的響應系統如下：

式（4）中：u為控制量；b為未知的控制系數（方向、大小均未知）。

本文的目的是在控制方向未知情況下，實現驅動系統和響應系統同步，換句話說就是當控制方向發生變化時，同步仍能實現，即，使得當t→∞時，有

定義驅動系統與響應系統的誤差為e=y-x，則分數階誤差系統可表示為

其第i（i=1，2，…，n）維分量可表示為

假設1：控制系數bi未知且有界，并在未知閉區間內取值，且0?Ii。

3　Nussbaum增益控制器設計

選取如下的滑模面：

式中，ci為正常數。

對式（7）兩邊沿時間求導得

不難證明此滑模面是穩定的。

對誤差系統（6），可設計如下虛擬控制量

式中，k0為正常數。

對于式（10），根據Lyapunov穩定性理論，si是漸近穩定的。

接下來，設計Nussbaum增益控制律為

將式（10）改寫為如下形式

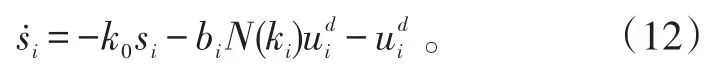
設計Nussbaum增益更新律為

構造如下Lyapunov函數

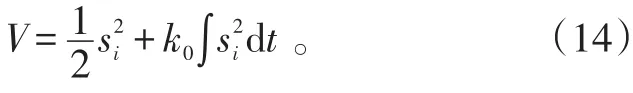
對式（14）兩邊關于時間求導得：

對式（15）兩邊積分得：

下面分析ki（t）的有界性。先假設ki（t）無界，且ki（t）→+∞。對式（16）兩邊除以ki（t），可得：

由Nussbaum函數的定義1及其性質式（1），可以推得：

此時，存在ki（t），使得當ki（t）→+∞時有：

而當ki（t）→+∞時，由式（17）的左邊，又有：

由式（17）～（19），結果顯然是矛盾的，即ki（t）→+∞的假設不成立。同理可以證明ki（t）→-∞的假設也不成立。因此，ki（t）是有界的。由式（7）、（14）和式（16）及混沌系統的特性容易得到V（t）有界，si有界，有界，再由Lyapunov函數的構造形式及其正定性，易得si→0。

4　數值仿真與分析

下面驗證本文Nussbaum增益控制方法的有效性。

以分數階Chen混沌系統作為驅動系統：

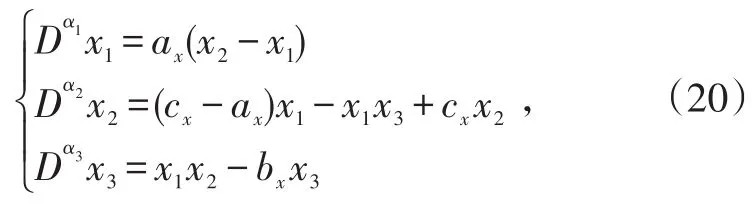
當ax=35，bx=3，cx=28時，整數階（αi=1）Chen系統表現出混沌狀態，仿真表明，當αi=0.95時，分數階Chen系統仍能表現出混沌行為［16］，當αi=0.9時，系統仍是混沌的。

構建帶控制輸入的分數階R?ssler系統作為響應系統：

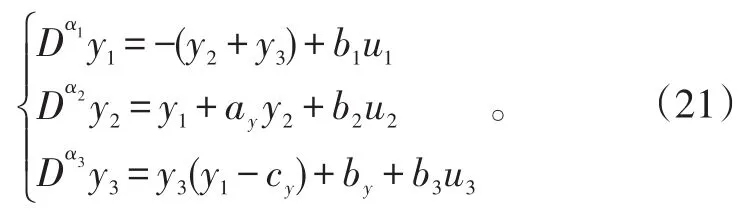
當ay=0.2，by=0.2，cy=5時，整數階Rssler系統表現出混沌狀態；當ay=0.4，by=0.2，cy=10，αi=0.9時，分數階R?ssler系統仍可得混沌吸引子［17］。

未知控制系數bi設置如下：

選取Nussbaum增益的初始值為ki（0）=（1，1，1）；驅動系統和響應系統的初始值分別為（x1（0），x2（0），x3（0））=（1，2，-1）和（y1（0），y2（0），y3（0））=（2，-1，1）；系統分數階次αi=0.9。

根據前面所設計的控制律式（11），得到的仿真結果如圖1所示。從仿真曲線可以看出，在控制方向切換時超調較大，這是Nussbaum增益控制進行方向搜索造成的。考慮Nussbaum增益控制的特性，其受初始狀態影響較大，當初始誤差較小時，穩定性會較好，但是，當誤差較大時，增益自適應調節律容易進入高增益區，使仿真結果發散。

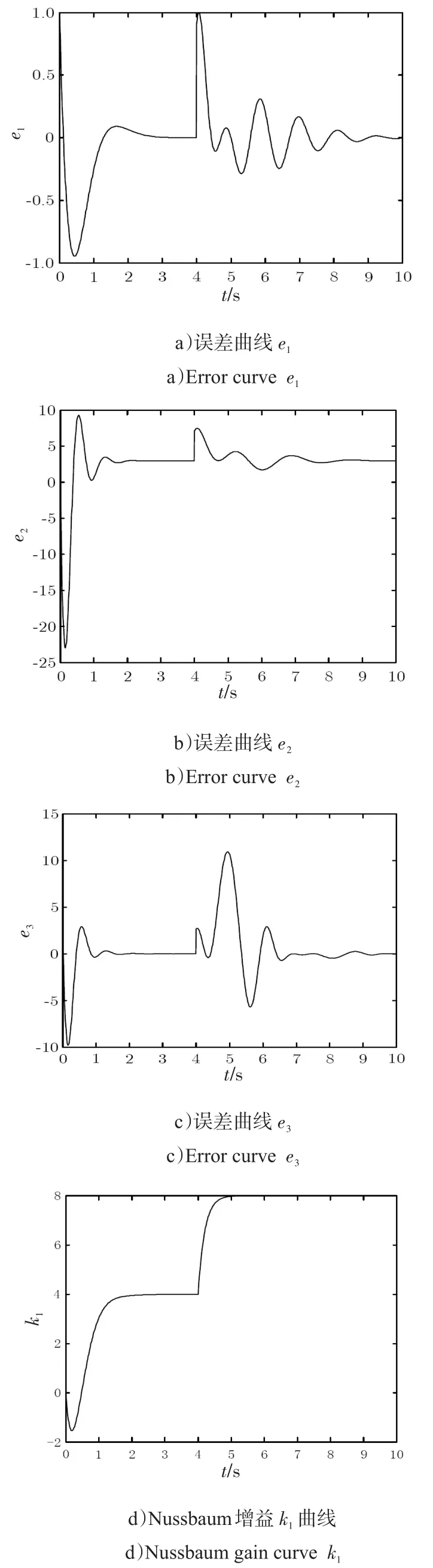
圖1　仿真曲線Fig.1 Simulation curves

5　結論

本文將Nussbaum增益控制引入分數階混沌系統，解決了分數階混沌系統在存在控制方向未知情況下的同步控制問題。首先，選取了一類穩定的分數階積分滑模曲面；然后，結合周愛軍等人設計的整數階Nussbaum增益控制方法，實現了分數階Chen系統和分數階R?ssler系統在控制系數未知情況下的混沌同步，仿真結果驗證了該方法的正確性和有效性。在同時考慮控制方向未知、增益受限和其他不確定因素影響的情況下，如何設計分數階混沌系統的同步控制是我們今后要進一步研究的課題。

［1］LEI J，WANG X，LEI Y.A Nussbaum gain adaptive synchronization of a new hyperchaotic system with input uncertainties and unknown parameters［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14（8）：3439-3448.

［2］ZHOU A，REN G，SHAO C，et al.Synchronization of chaotic systems by using limited nussbaum gain method［J］.Research Journal of Applied Sciences Engineering and Technology，2012，4（20）：4007-4011.

［3］劉濤，張皓，陳啟軍.通信受限網絡控制系統的H∞控制［J］.控制與決策，2013，28（4）：537-541. LIU TAO，ZHANG HAO，CHEN QIJUN.H∞control for networked control systems with communication constraints［J］.Control and Decision，2013，28（4）：537-541.（in Chinese）

［4］周愛軍.不確定混沌系統的控制與同步方法研究［D］.大連：大連海事大學，2012. ZHOU AIJUN.Research on control and synchronization methods for uncertain chaotic systems［D］.Dalian：Dalian Maritime University，2012.（in Chinese）

［5］DING Z.Adaptive control of non-linear systems with unknown virtual control coefficients［J］.International Journal of Adaptive Control and Signal Processing，2000，14（5）：505-517.

［6］王強德，井元偉，張嗣瀛.控制方向未知的非線性系統的自適應輸出跟蹤控制［J］.控制與決策，2006，21（3）：248-252. WANG QIANGDE，JING YUANWEI，ZHANG SIYING. Adaptive output tracking control of nonlinear systems with unknown control directions［J］.Control and Decision，2006，21（3）：248-252.（in Chinese）

［7］LIU L，HUANG J.Global robust output regulation of lower triangular systems with unknown control direction［J］. Automatica，2008，44（5）：1278-1284.

［8］BOULKROUNE A，M'SAAD M，CHEKIREB H.Design of a fuzzy adaptive controller for MIMO nonlinear time-delay systems with unknown actuator nonlinearities and unknown control direction［J］.Information Sciences，2010，180（24）：5041-5059.

［9］SAM GE S，YANG C，HENG LEE T.Adaptive robust control of a class of nonlinear strict-feedback discretetime systems with unknown control directions［J］.Systems&Control Letters，2008，57（11）：888-895.

［10］周平，鄺菲.分數階混沌系統與整數階混沌系統之間的同步［J］.物理學報，2010，59（10）：6851-6858. ZHOU PING，KUANG FEI Synchronization between fractional-order chaotic system and chaotic system of integer orders［J］.Acta Physica Sinica，2010，59（10）：6851-6858.（in Chinese）

［11］ZHOU P，DING R，CAO Y X.Multi drive-one response synchronization for fractional-order chaotic systems［J］. Nonlinear Dynamics，2012，70（2）：1263-1271.

［12］馬鐵東，江偉波，浮潔，等.一類分數階混沌系統的自適應同步［J］.物理學報，2012，61（16）：160506. MA TIEDONG，JIANG WEIBO，FU JIE，et al.Adaptive synchronization of a class of fractional-order chaotic system［J］.Acta Physica Sinica，2012，61（16）：160506.（in Chinese）

［13］李東，鄧良明，杜永霞，等.分數階超混沌Chen系統和分數階超混沌R?ssler系統的異結構同步［J］.物理學報，2012，61（5）：50502. LI DONG，DENG LIANGMING，DU YONGXIA，et al. Synchronization for fractional order hyperchaotic Chen system and fractional order hyperchaotic R?ssler system with different structure［J］.Acta Physica Sinica，2012，61（5）：50502.（in Chinese）

［14］黃麗蓮，齊雪.基于自適應滑模控制的不同維分數階混沌系統的同步［J］.物理學報，2013，62（8）：80507. HUANG LILIAN，QI XUE.The synchronization of fractional order chaotic systems with different orders based on adaptive sliding mode control［J］.Acta Physica Sinica，2013，62（8）：80507.（in Chinese）

［15］RYAN E.A universal adaptive stabilizer for a class of nonlinear systems［J］.Systems&Control Letters，1991，16（3）：209-218.

［16］YAN J，LI C.On chaos synchronization of fractional differential equations［J］.Chaos，Solitons&Fractals，2007，32（2）：725-735.

［17］LI C，CHEN G.Chaos and hyperchaos in the fractionalorder R?ssler equations［J］.Physica A：Statistical Mechanics and itsApplications，2004，341：55-61.

Nussbaum Gain Synchronization for Fractional-Order Chaotic Systems with Unknown Control Direction

WU Mei1，CHENG Jihong2a，YU Mingzhe3，ZHANG Youan2b
（1.Fire Monitoring Room，Yuhuangding Hospital，Yantai shandong 264001，China；2.Naval Aeronautical and Astronautical University a.Department of Scientific Research；b.Department of Control Engineering，Yantai shandong 264001，China；3.The 91526thUnit of PLA，Zhanjiang Guangdong 524064，China）

The Nussbaum gain control method was introduced to solve the synchronization control problem for fractionalorder chaotic systems with unknown control direction.Firstly，a fractional-order sliding motion was selected.Then，a Nussbaum gain controller was designed by combining the Nussbaum gain control method for integer-order systems and sliding mode variable structure control theory.Finally，an example was given，which realized the synchronization control between fractional-order Chen systems and fractional-order R?ssler systems with unknown control direction.Simulation results demonstrated the correctness and effectiveness of the presented method.

fractional-order chaotic systems；synchronization；Nussbaum gain control；unknown control direction

TN850.3

A

1673-1522（2016）03-0348-05DOI:10.7682/j.issn.1673-1522.2016.03.009

2016-03-18；

2016-04-20

國家自然科學基金資助項目（61273058）

吳梅（1962-），女，高工，大學。