新型無尾翼水下滑翔器升阻比性能的研究

呂鴻冠，黃　技*，王天霖，黃斯慧

（1.廣東海洋大學　工程學院，廣東　湛江　524088；2.大連海事大學，遼寧　大連　116026）

新型無尾翼水下滑翔器升阻比性能的研究

呂鴻冠1，黃技1*，王天霖2，黃斯慧1

（1.廣東海洋大學工程學院，廣東湛江524088；2.大連海事大學，遼寧大連116026）

采用標準k-ε兩方程渦粘性模型，壓力的隱式算子分割算法（PISO）求解時均Reynolds方程（RANS），對三種新型無尾翼水下滑翔器的升阻比性能進行研究。先對滑翔器摩擦阻力的CFD模擬結果與理論計算結果進行對比分析，驗證CFD模擬結果的合理性與可靠性；再對不同迎流速度、不同速度攻角下的試驗工況進行數值模擬，分析不同試驗工況下滑翔器的粘壓阻力與升力，得到不同試驗工況下滑翔器的升阻比性能。研究結果表明，新型無尾翼水下滑翔器在5°～15°攻角區間內具有良好的升阻比，小攻角下圓碟型和飛碟型滑翔器的升阻比性能優于橢圓型滑翔器，而大攻角下橢圓型滑翔器相對其它兩種具有更佳的升阻比性能，為新型無尾翼水下滑翔器升阻比性能的研究提供一定的思路。

水下滑翔器；無尾翼；升阻比；CFD

水下滑翔器是一種以浮標技術與水下機器人技術為基礎，依靠自身浮力驅動的新型海洋工程裝備。由于水下滑翔器與傳統的浮標和水下機器人相比，具有操控性高、靈活性強、續航時間久、數據采集密度大等特點，以及其在海洋開發、軍事勘察等領域的出色表現，水下滑翔器已逐漸發展為海洋工程裝備領域的熱門研究課題，受到很多工程師、科研人員等的高度關注。

目前，在整個世界范圍內，歐美國家的水下滑翔器技術較為成熟。歐美國家的水下滑翔器以Slocum、Seaglide、Spray等為典型代表［1-4］；21世紀初，日本東京大學TamakiUra實驗室研發了ALBAC水下滑翔器［5］，并在Sugura海灣進行試航；2005年，沈陽自動化研究所成功研發出中國第一臺水下滑翔器“Sea-Wing”；2010年，國家海洋技術中心開始從事淺海型水下滑翔器“Sun-Glider”的研制，直到今天已經廣泛應用于國內外海洋科學考察［6］；2015年國家“863”計劃項目資助的多家深海型水下滑翔器在南海進行了長航程集中海試比測，天津大學的深海型水下滑翔器“海燕”取得了最好的成績，這標志著我國第一款達到實用化水平的深海型水下滑翔器工程樣機的誕生。總的來看，國內的研究起步相對較晚，但也取得顯著的進展［6-8］。

近年來，世界各國加大了海洋資源的開發力度，對海洋工程裝備提出了更高的要求，傳統的水下滑翔器已經難以滿足實際的作業需求，一些學者總結了傳統水下滑翔器的弊端，提出了新型水下滑翔器的一些新功能、新模塊［6-8］。新型的水下滑翔器與傳統的水下滑翔器相比，對整體外觀設計、內部模塊集成、實際作業表現及自身的水動力性能都有更高的要求。

哈爾濱工程大學王天、葉秀芬等［9］對圓碟形滑翔器的航姿控制進行研究，在碟形滑翔器水動力性能的基礎上設計了控制系統算法；大連海事徐宏翔、王天霖等［10］對碟形浮標進行CFD數值計算，得到碟形浮標的水動力性能，上海交通大學張懷新、潘雨村等［11］對圓碟形滑翔器的阻力性能進行研究，得到碟形滑翔器的阻力規律。本文結合流體理論和CFD求解技術，對橢圓型（Ellipse）、圓碟型（Roundel）、飛碟型（Disk）三種新型無尾翼水下滑翔器進行分析，對滑翔器的阻力、升力及不同工況下的升阻比性能進行研究。

1　數值求解控制方程

笛卡爾坐標系下，水下滑翔器周圍的粘性不可壓縮三維流場的Navier-Stokes方程為：

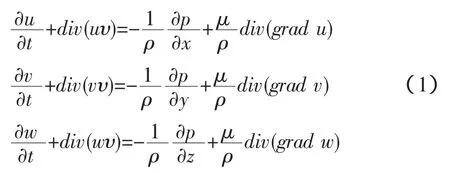
考慮滑翔器周圍流場湍流脈動的影響，對式（1）采用時均法，將湍流運動看成兩個流動疊加而成，一部分為時均流動，一部分為瞬時脈動流動。則Reynolds時均Navier-Stokes方程（RANS）定義為：

上述的RANS方程中引入了湍流脈動值的Reynolds應力項，需采用湍流模式對其進行封閉求解。這里采用標準k-ε兩方程渦粘性模型封閉RANS方程，算法采用求解瞬態迭代的PISO算法。

2　滑翔器選型及工況設計

滑翔器的選型一共三種：橢圓型（Ellipse）、圓碟型（Roundel）、飛碟型（Disk），如圖1所示：

圖1　Ellipse、Roundel、Disk滑翔器的三維模型

定義工況代號“DA0V0.1”，其中首項為滑翔器類型：D（Disk）、E（Ellipse）、R（Roundel）；第二項A（Angle）為攻角值；第三項V（Velocity）為速度值，如“DA0V0.1”代表飛碟形水下滑翔器0°攻角0.1 m/s迎流速度。則試驗工況如表1～表2所示：

表1　試驗工況表-不同迎流速度

表2　試驗工況表-不同速度攻角

3　滑翔器摩擦阻力的討論

3.1滑翔器的阻力構成

水中運動物體受到到的總阻力Rt由摩擦阻力Rf、粘壓阻力Rpv和興波阻力Rw組成，即：

對于大部分水中運動的物體，如水下機器人、水下滑翔器等，興波阻力Rw可忽略不計，則滑翔器運動時，受到的總阻力為：

由于水下運動物體的外型相對復雜，摩擦阻力Rf和粘壓阻力Rpv目前尚無成熟的理論體系直接求解。對于摩擦阻力Rf，目前大部分運用“相當平板假設”進行計算；而對于粘壓阻力，目前尚無理論進行計算，而是通過水池試驗或CFD技術進行研究。

3.2摩擦阻力系數

水中運動物體受到的摩擦阻力為：

式中：Cf為摩擦阻力系數；ρ為流體密度；v為迎流速度；S為濕表面積。

對于摩擦阻力系數Cf，目前主流的計算公式主要有邊界層速度指數型分布公式、Schoenherr公式、Prandtl-Schlichting公式、Hughes公式、1957ITTC公式。

（1）邊界層速度指數型分布公式

假設邊界層內的速度分布形式為指數分布，經過試驗結果修正后的指數分布公式為：

（2）Schoenherr公式

1932年Schoenherr運用邊界層速度為對數分布的假設，并依據平板拖曳試驗的數據，給出下列的摩擦阻力系數表達式：

上述公式為Schoenherr公式，1947年美國船模試驗池會議（ATTC）決定以該式作為摩擦阻力的標準公式，故此公式又稱為1947ATTC公式。

（3）Prandtl-Schlichting公式

Prandtl、Schlichting等人運用與1947ATTC公式相同的原則，得到與式（7）十分相似的Prandtl-Schlichting公式，該公式的表達式為：

（4）Hughes公式

1952年Hughes根據以往的平板試驗數據，提出平板摩擦阻力系數與展弦比有關的理論，給出以下公式：

（5）1957ITTC公式

1957年在西班牙馬德里召開的第八屆國際船模試驗池會議（ITTC）上根據幾何相似模型阻力試驗結果，認為Schoenherr公式、Prandtl-Schlichting公式等傳統的摩擦阻力計算公式在低雷諾數時偏低，于是提出了新的公式，叫做“1957年國際船模試驗池實船-船模換算公式”，簡稱1957ITTC公式：

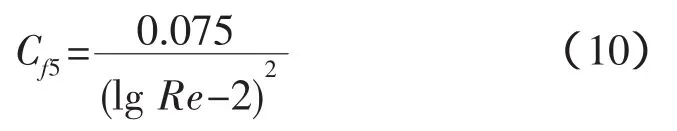
式（7）～式（8），式（10）為當前最常用的公式，式（7）在美國的應用最為普遍，式（8）在歐洲大陸的應用最為普遍。我國目前采用1957ITTC公式［12］。

4　數值模擬分析

4.1滑翔器的摩擦阻力

通過對比相同攻角、不同迎流速度下三種選型的CFD模擬結果與理論計算結果，驗證CFD模擬結果的合理性與可靠性。采用六面體結構網格占優法建立三種滑翔器的網格模型，在邊界壁面處（Wall）處采用非結構網格，流場區域采用結構網格；在迎流區域加密網格以捕捉滑翔器周圍流場的變化；滑翔器壁面劃分三棱柱邊界層網格，以精確捕捉滑翔器的升力、阻力信息。網格劃分信息如表3所示，邊界條件如圖2所示，核心區域網格如圖3所示。

表3　網格信息

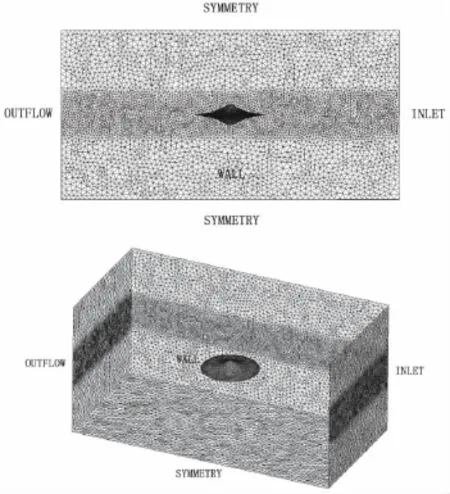
圖2　邊界條件設置

圖3　核心區域的結構網格

在標準k-ε兩方程渦粘性模型中使用標準壁面函數，以初始y+值為50作為基準，通過理論計算控制第一層邊界層網格厚度于0.005 m左右。每種計算工況均劃分5層邊界層網格，通過不斷調整第一層邊界層網格高度控制y+值在30~300之間，以保證第一層網格節點在粘性層流子層之上。如果第一層邊界層網格高度過小，即y+值低于30，則會導致第一層網格節點落入粘性子層，得到不準確的升力、阻力數據。一般來說，對于通常的湍流計算，y+在30~60之間可保證計算精度。

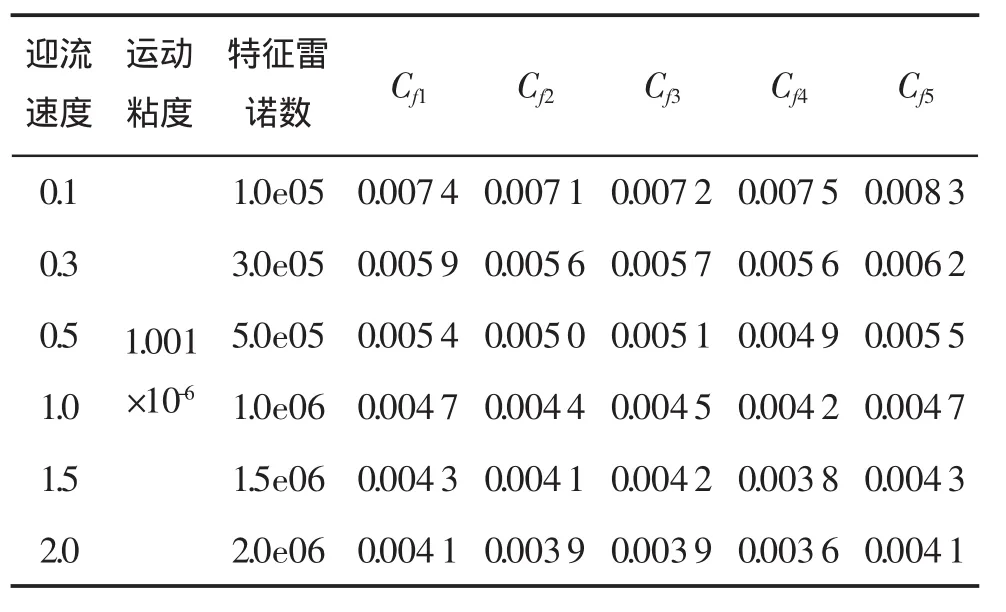
表4　不同經驗公式下的摩擦阻力系數

圖4　滑翔器理論摩擦阻力計算結果對比

從圖4第一張數據圖可看出，不同經驗公式計算的摩擦阻力系數基本差別不大。而Hughes公式相對其它公式偏小，這是因為Hughes公式是根據有限展弦比（三因次流動）平板數據外插得到的。總體來看，經驗公式的計算值基本分布在一個常數周圍。從圖4第二張到第四張數據圖還可看出，利用經驗公式計算滑翔器得到的摩擦阻力十分接近，阻力曲線基本呈現水平分布。

表5　滑翔器摩擦阻力的理論計算值

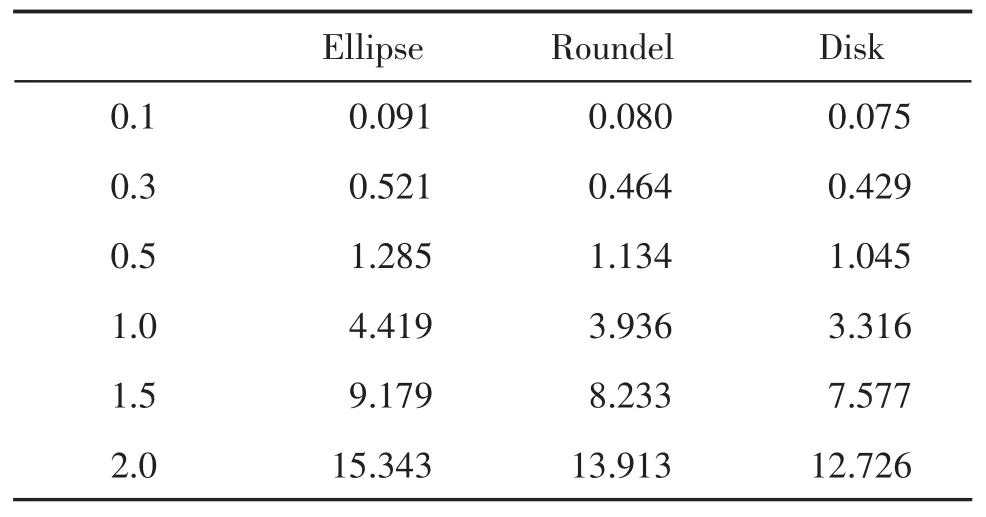
表6　滑翔器摩擦阻力的CFD模擬結果

從圖5可看出，滑翔器的摩擦阻力隨著迎流速度的增加而增加，且阻力變化趨勢近似拋物型，與摩擦阻力的計算公式（二次型）吻合得很好。對比圖5各條摩擦阻力曲線還可發現，CFD模擬結果與理論計算結果相當接近，每種外型的CFD摩擦阻力曲線與五條理論摩擦阻力曲線基本吻合，證明了每種工況的網格劃分方式、邊界層網格厚度定義，及各種求解參數設置的正確性。在此基礎上，可進一步討論滑翔器的在不同速度攻角下的升阻比性能。

圖5　理論計算結果與CFD模擬結果的對比

4.2滑翔器的粘壓阻力

粘壓阻力一直是流體力學中的難題，由于水下運動物體形狀的復雜性，目前尚無成熟的理論體系對其進行定量計算。但是，對粘壓阻力的定性分析，目前有較為成熟的理論體系。水下運動物體的粘壓阻力主要取決于物體的形狀及流體的流態，還與邊界層的流動情況有著密切的關系。新型滑翔器的三種不同選型在外觀上有著巨大的差別，故新型滑翔器的粘壓阻力是重要的水動力性能參數。

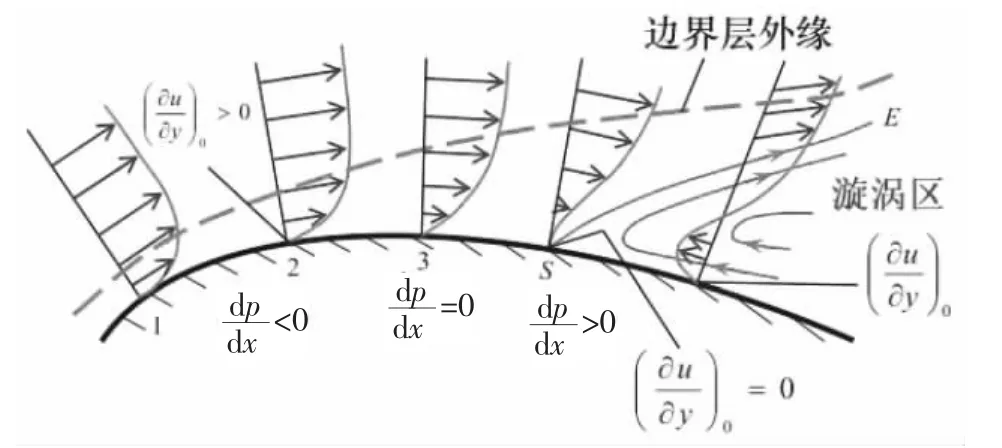
圖6　邊界層分離現象［13］

根據邊界層理論可知，當滑翔器在迎流方向的下游處滿足一定的條件時會出現粘性漩渦，導致滑翔器的粘壓阻力急劇增大。將滑翔器表面某一局部區域放大，如圖6所示。設邊界層外流體微團的速度在3時達到最大值Umax，壓力達到最小值Pmin。現在基于能量觀點，將滑翔器的繞流運動劃為3個過程分析滑翔器的粘壓阻力。

第一個過程：則從1到3區間內，滑翔器邊界層外部的流體微團速度呈遞增趨勢，呈壓力遞減趨勢，此區域為順壓梯度區。當流體微團到達3時，壓能全部轉化為動能，此時速度達到最大值Umax，壓力達到最小值Pmin。

第二個過程：超過3點后，壓力沿著流動方向呈遞增趨勢，流體微團開始進入逆壓梯度區。從力學理論分析可知，在順壓梯度區時，流體微團雖然受到粘性剪應力的作用，但是在正壓梯度下，流體微團仍擁有足夠的動能順利前進，在3處達到最大速度Umax。當流體微團經過3后，進入了逆壓梯度區，此時流體微團的動能不僅要轉化為壓能，而且還要提供一部分能量克服粘性阻力做功，在這雙重阻礙下，流體微團的動能不斷降低。

第三個過程：當流體到達S點的時候，動能被完全消耗，速度降為0，此時在逆壓梯度的作用下，流體微團開始回流。從流體理論可知，滑翔器邊界層外的流體與來流速度相同，而邊界層內的速度與來流速度相反，故在尾部處出現回流，產生了粘性漩渦。這部分漩渦的維持需要不斷消耗能量，導致滑翔器表面邊界層分離點下游的壓力無法繼續升高，保持著和分離點一樣的壓力值。經過上述分析可知，滑翔器的前后存在一個壓力差，滑翔器運動的時候需要克服這個壓力差做功，必須消耗額外的能量，這便是是滑翔器粘壓阻力的由來。

實際上，繞流過程不一定會產生邊界層分離現象。如果將物體設計成流線型，可大大降低邊界層分離的幾率。另外，邊界層是否分離還與速度攻角有著非常大的聯系，即使是流線型物體，在小攻角情況下無分離，但是在大攻角的情況下便可能會發生分離。

表7　不同速度攻角下滑翔器的粘壓阻力

圖7　不同速度攻角下滑翔器粘壓阻力的變化趨勢

從圖7可明顯看出，Disk滑翔器的粘壓阻力隨著迎流速度的增大而急劇增大，而Ellipse滑翔器的變化則十分緩和。尤其當速度攻角為45°時，Disk滑翔器的粘壓阻力為Ellipse滑翔器的5倍。根據上述的分析結果可推測，造成這種現象的根本原因在于Disk滑翔器與Ellipse滑翔器外觀的巨大差異，導致兩者的粘壓阻力出現極大的差別。Disk滑翔器對速度攻角的變化十分敏感，即隨著速度攻角的變化，邊界層分離現象會明顯加劇，迎流后方出現強漩渦區，導致粘壓阻力的急劇增大。而Ellipse滑翔器對速度攻角變化的反應相對緩和，邊界層分離現象不明顯甚至不出現邊界層分離現象。

下面根據流場的分布情況來驗證推論的準確性。15°，25°，35°，45°速度攻角的工況下，Disk滑翔器和Ellipse滑翔器周圍的流場分布如圖8～圖9所示：

圖8　15°，25°，35°，45°速度攻角下Disk滑翔器周圍流場的分布情況

圖9　15°，25°，35°，45°速度攻角下Ellipse滑翔器周圍流場的分布情況

從圖8～圖9可看出，Disk滑翔器對速度攻角的變化非常敏感。當速度攻角為15°時，邊界層分離現象不明顯，而當速度攻角增加到25°時，迎流方向的后背處開始出現漩渦，從圖7可得知此時粘壓阻力會大幅度增加，接近翻倍；而Ellipse滑翔器的粘壓阻力增加非常小，幾乎不變。當速度攻角達到45°時，Disk滑翔器在迎流方向的后背處出現強漩渦，此時粘壓阻力急劇加大，而Ellipse滑翔器粘壓阻力增加值相對較小，邊界層分離現象不明顯甚至不出現邊界層分離。造成這種現象的根本原因是Ellipse滑翔器更符合流線型外觀設計，Ellipse滑翔器貼體流場變化相對緩和，不會出現巨幅震蕩，故大攻角時Ellipse滑翔器更具有實際的應用價值。

4.3滑翔器的升阻比

滑翔器的升阻比如表8~表10、圖10所示。

表8　不同速度攻角下Ellipse滑翔器的升阻比

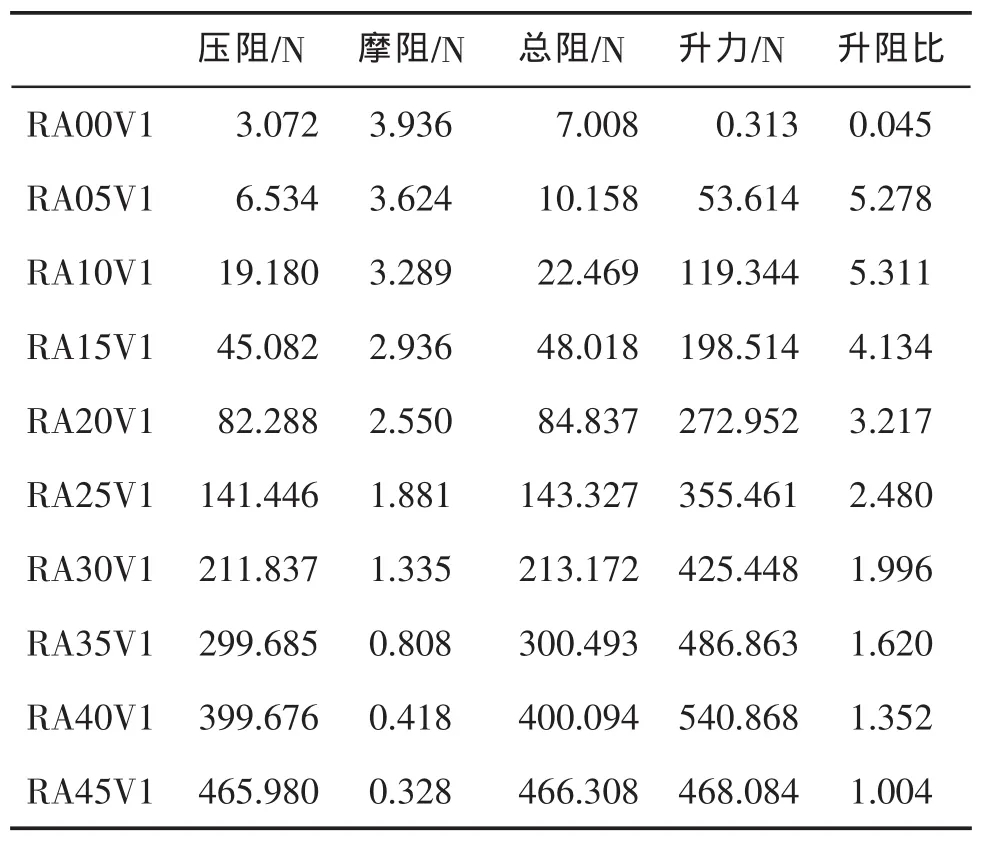
表9　不同速度攻角下Roundel滑翔器的升阻比

表10　不同速度攻角下Disk滑翔器的升阻比

圖10　滑翔器在不同速度攻角下的升阻比性能

從圖10可看出，無論哪種選型的滑翔器，升阻比均呈現先升高后降低的趨勢。在5°~15°速度攻角范圍內，滑翔器的升阻比達到最大值。在小攻角情況下，Disk滑翔器和Roundel滑翔器相對Ellipse滑翔器具有更優的升阻比性能；而在大攻角情況下，Ellipse滑翔器以其優良的流線型外觀在升阻比性能方面表現出巨大的優勢。

5　總結

利用流體理論與CFD求解技術對三種新型無尾翼水下滑翔器的升阻比性能進行研究，得到了滑翔器重要的升阻比性能參數。滑翔器在速度攻角為5°~15°的范圍內具有良好的升阻比性能。在小攻角情況下，Roundel滑翔器和Disk滑翔器的升阻比性能表現優于Ellipse滑翔器；而在大攻角情況下，Ellipse滑翔器的升阻比性能相對Roundel滑翔器和Disk滑翔器更具實際應用價值。

［1］SStommel.The SlocumMission［J］.Oceanography，1989，2（1）：22-25.

［2］Douglas C Webb，Paul J Simoneai，Clayton P Jones.SLOCUM：An Underwater Glider Propelled by Environmental Energy［J］.IEEE Journal ofOceanic Engineering，2001，26（4）：447-452.

［3］Eriksen C C，Osse T J，Light R D，et al.Seaglider：A Long-Range Autonomous Underwater Vehicle for Oceanographic Research［J］.IEEE Journal ofOceanic Engineering，2001，26（4）：424-436.

［4］JeffS，Russ E D，Owens W B，et al.The Autonomous Underwater Glider"Spray"［J］.IEEE Journal of Oceanic Engineering，2001，26（4）：437-446.

［5］Tomoda Y，Kawaguchi K，Ura T，et al.Development and Sea Trials of a Shuttle Type AUV ALBAC［C］//8th Int.Symposium on Unmanned Untethered Submersible Tech，1993：7-13.

［6］溫浩然，魏納新，劉飛.水下滑翔機的研究現狀與面臨的挑戰［J］.船舶工程，2015，01：1-6.

［7］李志偉，崔維成.水下滑翔機水動力外形研究綜述［J］.船舶力學，2012，07：829-837.

［8］李杰，周興華，唐秋華，等.水下滑翔機器人研究進展及應用［J］.海洋測繪，2012，01：80-82.

［9］王天.新型碟形水下機器人及其航姿預測控制系統研究［D］.哈爾濱：哈爾濱工程大學，2013.

［10］徐宏翔.基于CFD模擬方法的圓碟型浮標水動力分析［D］.大連：大連海事大學，2014.

［11］張懷新，潘雨村.圓碟形潛水器阻力性能研究［J］.上海：上海交通大學學報，2006，06：978-982+987.

［12］盛振邦，劉應中.船舶原理［M］.上海：上海交通大學出版社，2003.

［13］王家楣，張志宏，馬乾初.流體力學［M］.大連：大連海事大學出版社，2010.

［14］孟凡豪，嚴天宏，何波，等.水下滑翔器整體外形設計及水動力性能分析［J］.海洋工程，2014，02：61-71.

Research on a New Type of Tailless Underwater Glider

LV Hong-guan1，HUANG Ji1，WANG Tian-lin2，HUANG Si-hui1
1.College of Engineering，Guangdong Ocean University，Zhanjiang 524088，Guangdong Province，China；
2.Dalian Maritime University，Dalian 116026，Liaoning Province，China

This paper uses the standard κ-ε two equation eddy viscosity model and the pressure implicit with splitting of operators（PISO）algorithm to solve the Reynolds-Averaged Navier-Stokes（RANS）equation for studying three new types of tailless underwater gliders in their lift-drag ratio performances.The CFD simulation results are compared with the results of theoretical calculation of the friction of the glider for verifying the rationality and reliability of the CFD simulation results.Then numerical simulation is conducted for the experimental states under different approach speeds and different speeds of attack angle，in order to analyze the viscous-pressure resistance and elevating force，obtaining the lift-drag ratio performances of gliders under different experimental states.The research results show that the new type of tailless underwater glider has a good performance in lift-drag ratio between the 5 to 15 degree attack angle.It is showed that the lift-drag ratio of the Roundel or Disk glider is higher than that of Ellipse glider under small attack angle，while the Ellipse glider has a higher lift-drag ratio than others under large attack angle.The study results provide some ideas for the research of new-type tailless underwater gliders.

underwater glider；tailless；lift-drag ratio；CFD

U661.31；P715.5

A

1003-2029（2016）04-0011-09

10.3969/j.issn.1003-2029.2016.04.003

2015-11-26

廣東省青年創新人才類項目資助（2014KQNCX086，2014KQNCX081）；廣東省大學生科技創新培育專項資助項目（pdjh2016a0226）

呂鴻冠（1994-），男，主要研究方向為船舶與海洋工程。E-mail：lhggzyx2015@163.com

黃技（1988-），男，碩士，講師，主要研究方向為船舶與海洋結構設計。E-mail：dmuhuangji@163.com