非線性光束傳輸方程的tanh-coth解法

徐偉津，卓輝

（湖南農業大學信息科學技術學院，長沙410128）

非線性光束傳輸方程的tanh-coth解法

徐偉津，卓輝

（湖南農業大學信息科學技術學院，長沙410128）

非線性薛定諤方程的解析解的分析對研究信息的傳輸有著非常重要的作用，利用tanh-coth法求非線性薛定諤方程得到一系列較好的解析解，對研究光束的非線性傳輸具有一定的指導意義。

光孤子；非線性薛定諤方程；tanh-coth法

0　引言

自然界的非線性現象是一個普遍問題，而且都可以用非線性薛定諤方程來描述。在非線性光學研究中，也同樣可以用非線性薛定諤方程來描述。從上個世紀開始，非線性光學的非線性薛定諤方程已經成為研究的熱點，其中對介質中的光束演化的研究也是一個非常重要的問題，其研究成果指導了許多光控制器件的開發。孤子的現象與孤子概念的提出可以追溯到20世紀30年代，起初人們是在水中發現了孤子現象，1973年，光孤子的概念首次提出：光孤子與其他同類光孤子相遇后，其形狀，速度，幅度將不會發生變化，隨后對其進行了深入研究并推廣開來。當前，研究者已經陸續建立了KDV方程［1］，S-G方程，K-G方程［2］及非線性薛定諤方程來描述孤子的相關變化，當前有很多研究者利用逆反射法［3］，Painleve展開法［4］，Hirota雙線性法［5］，變分法，數值法等，來解決光學的非線性傳輸特性問題，得到了非常重要的結論。其中D.Anderson利用變分法求解了光脈沖在光纖中的非線性傳輸的非線性薛定諤方程得到了啁啾和波包寬度的演化情況［6］，沒有給出一個定量的具體的解析解，但非常簡潔。本文則著眼于tanh-coth法［7］在非線性薛定諤方程在光孤子通信中的求解，得到了一系列相對較好的解析解。對于光束在非線性介質的傳輸研究有著重要的研究作用。

1　傳輸方程與tanh-coth法

1.1傳輸方程簡介

在橫向X方向上折射率具有線性周期調制的自聚焦克爾型非線性介質中，光束沿縱向Z方向的傳輸方程在弱調制近似下滿足下面的非線性薛定諤方程：

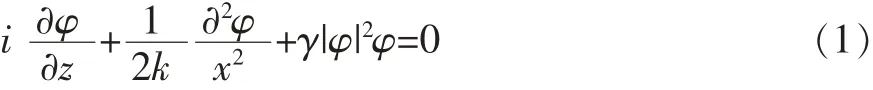
式中，k=n0ω/c=2πn0/ρ，n0是線性折射率，ρ是ρ射光束的波長，γ是介質的。

1.2對于非線性偏微分方程

引入w=x-ct，則將方程（2）化成常微分方程如下：

再引入一個新的獨立變量，令：

則有：

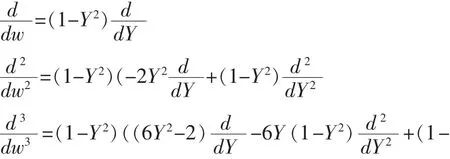
2　簡化的傳輸方程求解

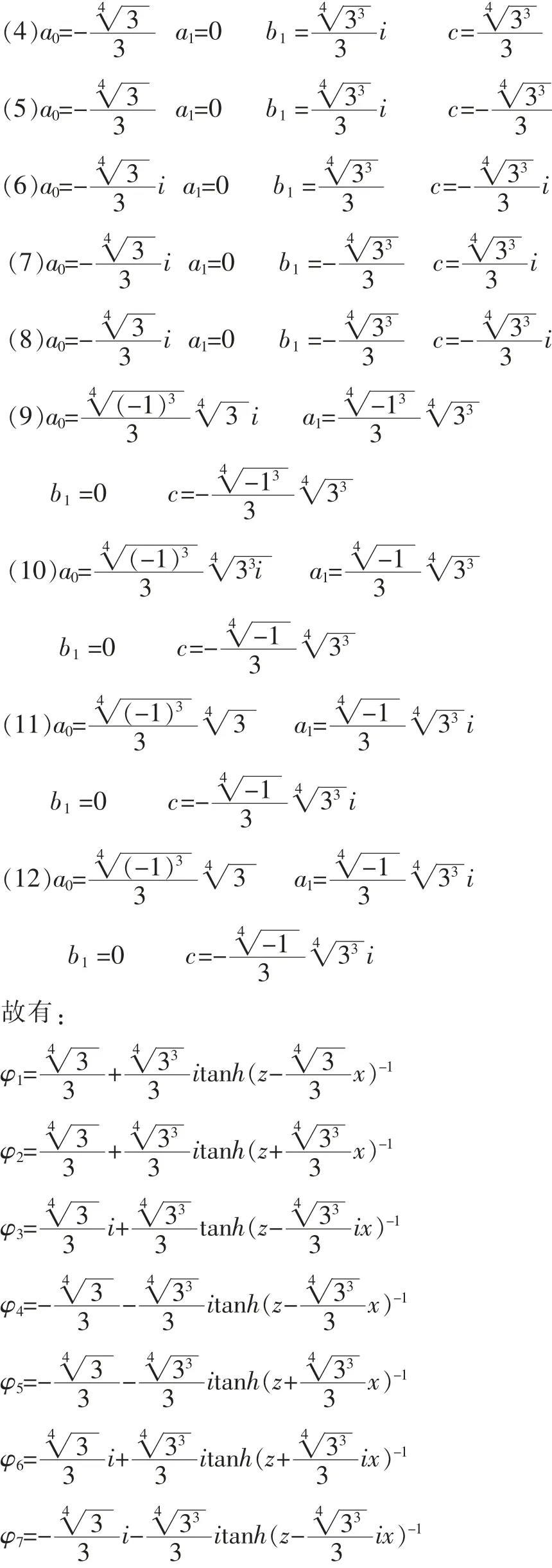
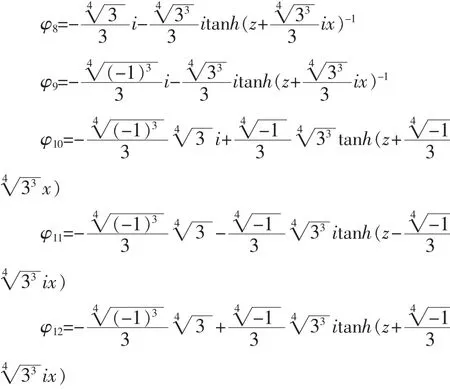
與D.Anderson用變分法求解的結果比較發現，D. Anderson研究了光脈沖在光纖中的非線性傳播的傳輸方程，假設輸入脈沖為，經過傳輸介質后光脈沖假定形式為（x））+ib（x）τ2）通過變分分析，D.Anderson得到了Ax、a（x）、b（x）的演化關系，能很好地分析光脈沖的演化情況，而本文通過tanh-coth方法得到了一系列的具體的解，這對問題的分析有更好的指導作用。

3　結語

本文運用tanh-coth方法求出了簡化的光束在弱調制情況下的傳輸方程的解析解，通過求解過程可以看出tanh-coth方法解非線性方程十分的簡潔，易懂，直觀，而且能夠得到十分豐富的解的數據，能夠幫助我們更好地分析和研究相關的非線性方程。

［1］廖歐，舒級，曾群香.一類混合KDV方程的精確孤立波解［J］.四川師范大學學報：自然科學版，2015（4）：493-496.

［2］董孝義.光孤子通信原理與進展［J］.光通信技術，1992，16（2）：28-39.

［3］Ablowitz M J，Segur H.Solitons and Inverse Scattering Transform［M］.Philadelphia：SIAM，1981.

［4］樓森岳.推廣的Painlevé展開及KdV方程的非標準截斷解［J］.物理學報，1998，47（12）：1937-1945.

［5］張解放，郭冠平.（2+1）維破裂孤子方程的新多孤子解［J］.物理學報，2003，52（10）：2359-2362.

［6］Anderson D.Variational Approach to Nonlinear Pulse Propagation in Optical Fibers［J］.Physical review A，1983，27（6）：3135.

［7］Gzükizil F，Salhi A.New Travelling Wave Solutions of Two Nonlinear Physical Models by Using a Modified Tanh-Coth Method［J］. Journal of Algorithms&Computational Technology，2015，9（1）：1-12.

The tanh-coth Solution to the Beam Nonlinear Transmission Equation

XU Wei-jin，ZHUO Hui
（Institude of Information and Science Technology，Hunan Agriculture University，Changsha 410128）

Analyzing the analytic solutions of Nonlinear Schrodinger equation plays a significant role in studying the transmission of information.Uses the tanh-coth method to solve Nonlinear Schrodinger equation and gets a series of decent analytic solutions，which makes a positive difference in studying the nonlinear transmission.

Optical Soliton；Nonlinear Schrodinger Equation；tanh-coth Method

1007-1423（2016）23-0013-03DOI：10.3969/j.issn.1007-1423.2016.23.003

徐偉津（1994-），男，湖南永州人，學生，專業方向為主攻非線性傳輸

卓輝，博士，副教授，研究方向為從事光的非線性、光孤子等理論，E-mail：zhuohuitxh@163.com

2016－05－10

2016－08－05