“一類與橢圓有關的最值問題”的教學分析①
陶新芝
(江蘇省昆山中學,昆山 215300)
?
“一類與橢圓有關的最值問題”的教學分析①
陶新芝
(江蘇省昆山中學,昆山215300)
圓錐曲線是高中解析幾何的核心內容,其最值問題是與不等式、函數密切相關的具有較強綜合性的問題.掌握與橢圓有關的最值問題,不僅有助于學生分析問題和解決問題能力的培養,還能夠通過滲透數形結合、化歸與轉化等數學思想,增強思維的靈活性.那么,如何更加有效地指導學生學習“與橢圓有關的最值問題”呢?筆者在實踐中進行了多次嘗試,并獲得一些有意義的經驗.
教學中,筆者先通過多媒體向學生演示了“運動的太陽系”,并請學生結合所學知識,從數學角度研究地球公轉過程中,地球距離太陽中心的最近和最遠的距離.其設計意圖在于,利用天體運動中所蘊含的數學問題激發學生的學習興趣,使學生主動引入平面直角坐標系,用代數的方法思考幾何問題,以體現解析幾何的本質,并通過把實際問題轉化為數學問題,體會數學知識的實際應用價值.
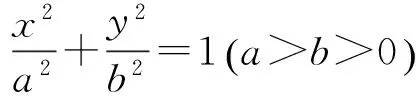
分析:求定點到橢圓上的任意點之間距離的最值問題,常用兩點間距離公式求解,通過消元將該問題轉化成二次函數的最值問題,用代數方法解決幾何問題.或者考慮F點的特殊性,利用橢圓的第二定義,將兩點間的距離問題轉化為橢圓上點到直線的距離問題,采用數形結合的方法加以解決.
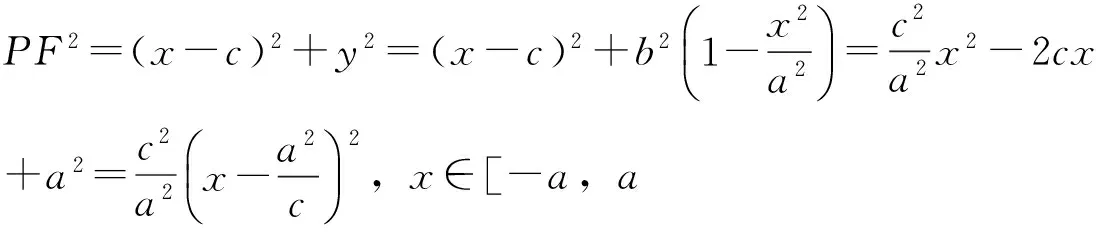
當x=-a時,PFmax=a+c;
當x=a時,PFmin=a-c.
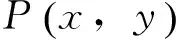

通過觀察圖形并結合運動的觀點(動橢圓上的點定直線或動直線定橢圓)得:
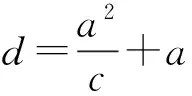
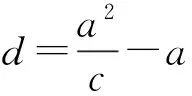
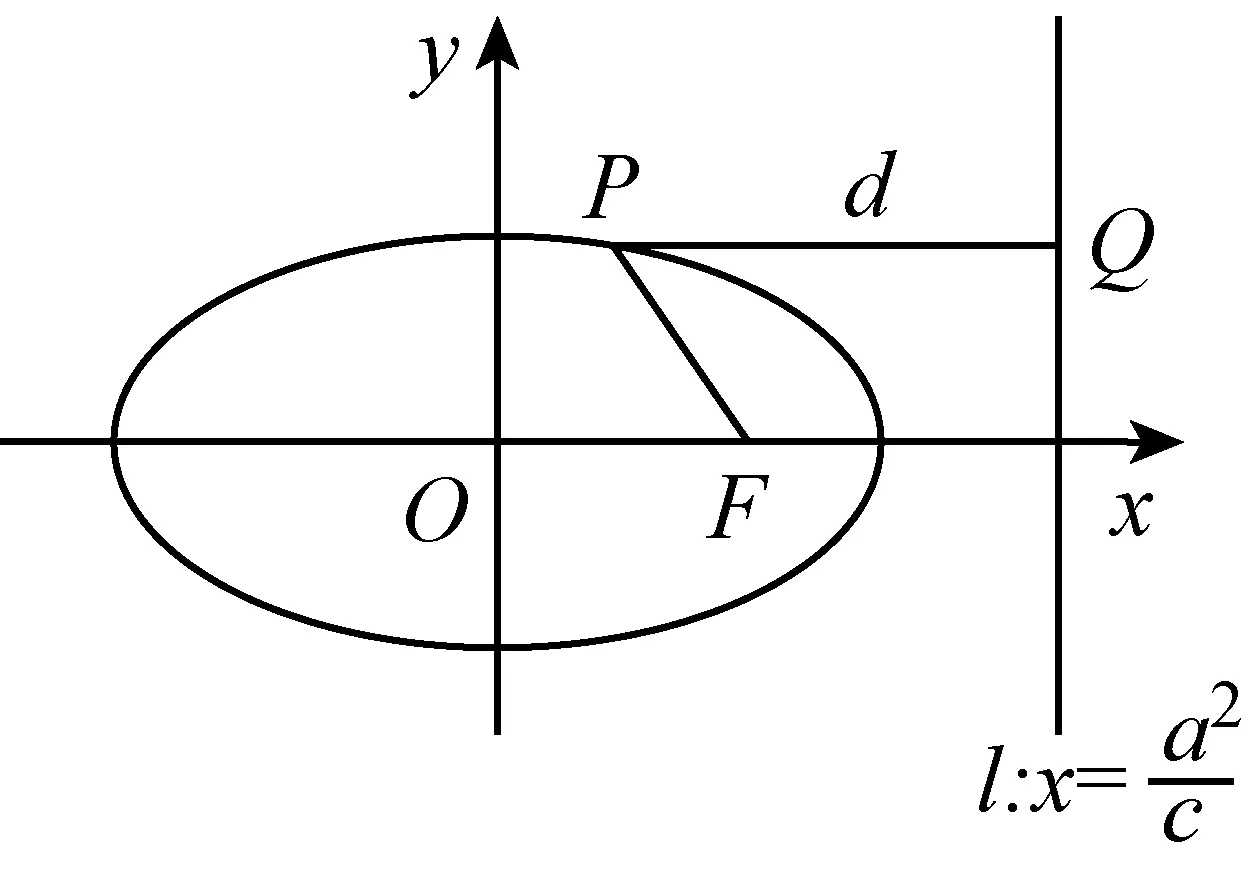
圖1
本題是研究焦點到橢圓上任意點的距離的最值問題,目的是引出解決此類最值問題的兩種基本方法,即函數法和定義轉化法.由上題的研究可以發現,橢圓的右頂點是到右焦點最近的點,其對應的位置在太陽系中稱為近日點;橢圓的左頂點是到右焦點最遠的點,其對應的位置在太陽系中稱為遠日點.教學中可引導學生思考:如果定點是長軸上除焦點外的其他點,這個結論成立嗎?由此進行下面的探究.
分析:用兩點間距離公式求解,通過消元將問題轉化成二次函數的最值問題.解題過程中需要關注目標函數的定義域.
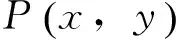
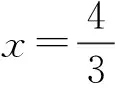
當x=-2時,PM2max=9?PMmax=3.
教師再結合地球公轉問題,引導學生思考,如何計算地球距太陽表面的最近距離.通過回歸實際,從學生的直觀感知出發得到問題的解決方法,并揭示該問題的本質,即橢圓上任意一點到圓上任意一點距離的最值.

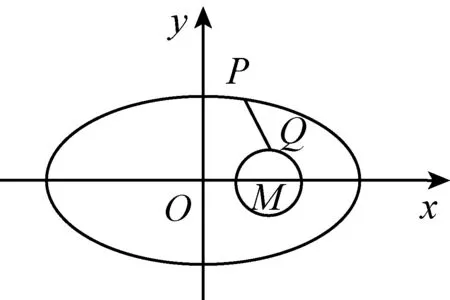
圖2
分析:此題有兩個動點,考慮先確定一個,利用圓的性質,可知PQmin=PMmin-r,再利用探究問題1的結論即可求得PQmin,則問題得到解決.這個變式是對探究問題1的強化,難點在于對兩個動點的處理.利用圓的性質突破難點,這是化歸思想的具體應用.
解:設圓M的半徑為r,
由圓的性質和題意,可知PQmin=PMmin-r.
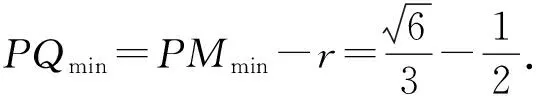
在經典問題的幾何法解題過程中,我們采用數形結合的方式研究了橢圓上的點到與x軸垂直的直線距離的最值問題,如果直線不垂直于x軸,應該怎樣解決?

分析:求橢圓上的點到直線距離的最值問題,可以利用點到直線距離公式構建二元目標函數,再用解決二元最值問題的基本方法來解決;或者借鑒解決經典問題時動直線定橢圓的操作過程,得到平行于已知直線的直線與橢圓相切時切點到直線的距離最近,而最近距離等于切線到已知直線的距離.
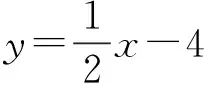
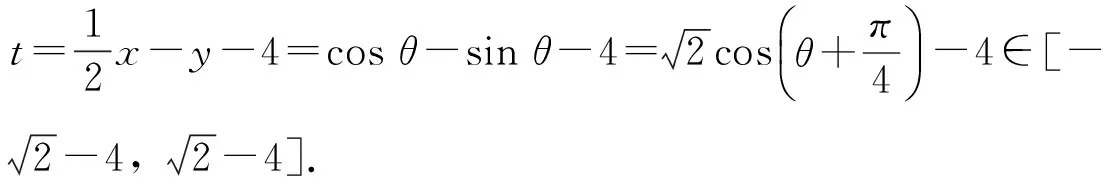
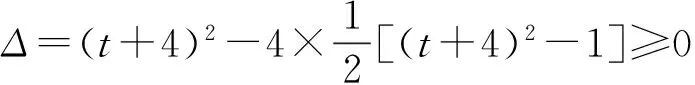
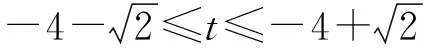
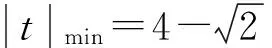
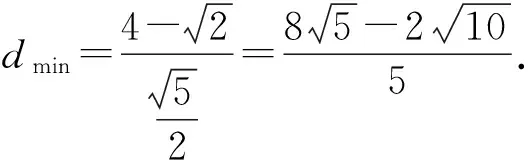
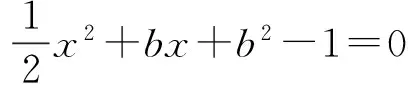
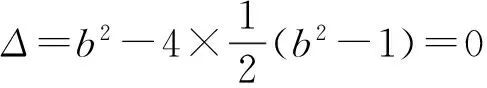
解此類問題時,學生很容易想到代數法和幾何法這兩種解題途徑.大部分學生利用代數法解題時會在消元的時候遇到困難;而利用幾何法解題時,計算切點又過于復雜.因此可以組織學生進行分組討論,最后歸納總結:當目標函數不便于直接消元時,可以利用三角換元或者目標函數的幾何意義找到解題的突破口.求圓錐曲線上的點到某條直線距離的最值時,利用數形結合思想先求與已知直線平行的且與圓錐曲線相切的直線方程,再求兩平行線之間的距離可以避免煩瑣的計算.
在“一類與橢圓有關的最值問題”的課堂教學中,筆者運用了系統的方法分析教學問題,建立了解決問題的策略方案.這個過程的科學化運作是行為主義、建構主義等教學設計理論有機結合的結果.
行為主義認為學習是一種行為的變化,強調刺激、反應和強化.這種理論給教學設計的啟示是:(1)反應必須在刺激之后立即出現;(2)重復練習能加強學習和促進記憶;(3)與反應正確性有關的信息可以促進學習.本節課在完成例題的解答后,利用探究問題1及兩個變式,探究問題2和探究問題3不斷刺激,促使學生學習和反復操練,達到強化和鞏固的目的.
建構主義認為,學習者要真正獲取知識,是學習者在一定社會文化背景和情境下,利用必要的學習資源,通過與他人的協商、交流與合作,由本人進行意義建構而獲得的.建構主義強調創設情境,并使學習者進入情境;強調為學習者提供各種資源,讓學習者自主學習和探究;強調組織學習者之間進行協商學習.根據建構主義學習理論,教學設計必須體現的是:(1)強調“情境”的重要性;(2)強調以學生為中心;(3)強調“協作學習”的重要性.根據這種教學設計理論,本節課設置并圍繞太陽系行星公轉的情境,不斷提出問題,促使學生充分利用已有的知識體驗和生活經驗進行獨立思考、分組討論和交流總結,努力實現課程改革中“以學生為本”的基本理念.
根據這兩種理論的結合,本節課利用多媒體課件輔助教學,直觀形象地展示了問題情境,圍繞情境不斷提出與橢圓有關的最值問題,層層遞進反復強化,始終貫徹以教師為主導,學生為主體,探究為主線,引導學生主動參與到課堂教學的全過程中.從教學效果上看,這種實踐是非常有益的.
(責任編輯:李珺)
① 本文系江蘇省中小學教學研究2013年度第十期立項課題《普通高中師生共建教學問題庫的實踐》(編號:2013JK10-L086,主持人:姜紅珍、胡福林)的研究成果之一.

