非全包裹超空泡航行體建模與反演變結構控制

李洋，劉明雍，張小件，彭星光

(西北工業大學航海學院，陜西西安 710072)

非全包裹超空泡航行體建模與反演變結構控制

李洋，劉明雍，張小件，彭星光

(西北工業大學航海學院，陜西西安 710072)

超空泡航行體動力學系統存在高度非線性及多變量耦合等問題，非全包裹超空泡使其受力更為復雜，給控制系統設計造成諸多困難。針對超空泡航行體的以上特點，開展了對非全包裹超空泡航行體控制系統的研究，在通過受力分析建立其動力學模型基礎上，設計了超空泡航行體的反演變結構控制器，并證明了系統穩定性。仿真結果驗證了該控制器對超空泡航行體穩定航行及跟蹤控制的有效性。

非全包裹；超空泡航行體；建模；反演變結構控制

因利用一層氣體包裹航行體，使其僅有很小部分與水接觸，減少了附加質量和阻尼力矩，超空泡技術為水下航行體帶來高速航行可能性的同時，也使航行體對外界干擾更加敏感，動力學建模、制導與控制等方面更加困難［1-6］。

超空泡根據空泡形狀的不同可以分為全包裹與非全包裹兩大類。目前，研究大多集中于全包裹超空泡技術中。Vanek等［1］對超空泡航行體縱向動力學模型非線性項里的滑行力進行重點研究，并通過滾動時域控制對航行體進行了跟蹤控制的研究。Dzielski［2］建立了全包裹超空泡航行體的非線性模型并利用反饋線性化進行處理。Mao等［3］考慮了尾舵效率n的不確定性，將其視為未知參量并通過自適應控制的方法實現對超空泡航行體的跟蹤控制。Kirschner等［4］研究了空泡結構對航行體動力學模型的影響。Yu等［5］利用有限元方法對超空泡的形成，航行體在機動過程與空泡的相互作用等內容進行了研究。Li等［6-7］考慮空泡變化的時延效應，并進行了相關試驗。Mokhtarzadeh等［8］研究了3種不同形狀空化器對航行體穩定性的影響，以及不同空化數對空泡形成的影響，同時也對上述不同情況下航行體產生的滑行力進行了分析和研究。目前，研究大多集中于全包裹超空泡技術中，而對非全包裹超空泡的研究還十分欠缺，僅Kim等［9］提到超空泡形成的過渡階段等相關內容，但其研究重點在于從物理角度出發，研究在非全包裹超空泡的狀態下，航行體的受力情況，對該狀態下的航行體控制系統研究較少。非全包裹超空泡，即空泡不完全包裹航行體，而閉合在航行體尾部之前，這就造成航行體尾部仍受到浮力作用［9］。在實際航行中，當航行速度下降或者空化器通氣不足時，空泡自然會縮短，非全包裹超空泡航行不可避免。與全包裹超空泡相比，非全包裹超空泡狀態下的航行體受到的阻力增加，因航行體處于2種介質之中受力更為復雜。因空泡外形改變，不再適用已有全包裹超空泡的動力學模型，有必要對非全包裹狀態下航行體的動力學特性進行研究。

本文以非全包裹超空泡航行體為研究對象，首先對該狀態下的航行體進行受力分析，進而建立動力學模型并分析其零輸入狀態響應性能；然后設計了一種反演滑模控制器來完成對航行體的復合控制；最后通過仿真驗證，表明該控制系統具有較好的控制效果。

1　非全包裹超空泡航行體動力學建模

本文研究模型為無尾舵航行體，利用頭部空化器偏轉及尾部直接側向力控制航行體姿態，且其上下、左右均相互對稱，不考慮橫滾的情況下，運動可解耦為縱平面及水平面2個平面運動［10］。以縱平面運動分析為例，其頭部空化器可偏轉一定角度，利用合理的通氣及航行體外形設計使空泡閉合于航行體尾部即直接側向力作用前端。如此，該航行體受力如圖1所示。分為頭部空化器阻力且與尾部推力相同，空化器升力，自身重力，直接側向力，尾部浸入海水部分所受浮力以及尾部上下表面所受的壓力差。

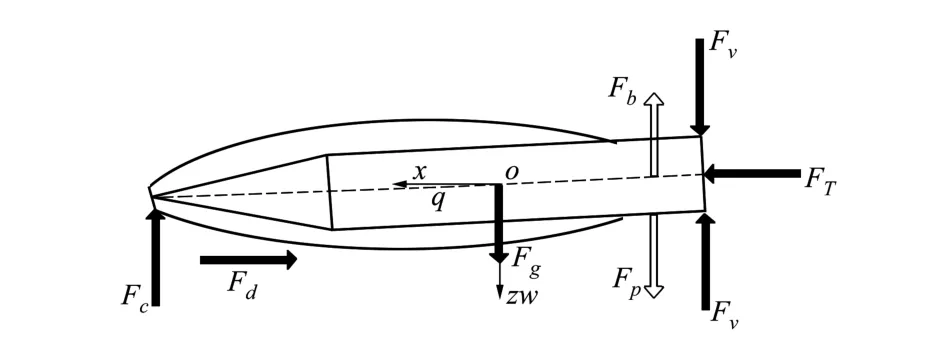
圖1　超空泡航行體受力分析圖

考慮頭部空化器為圓盤形，主體前1/3部分為圓錐，后2/3部分為圓柱，總長度用L表示［7］。描述航行體運動的坐標系取重心處為原點o，三軸分別為沿發射方向水平的x軸，垂直于x軸水平向右的y軸及垂直平面豎直向下的z軸。其中航行體質量為m，x軸方向上速度為V，繞橫軸轉動慣量為Jy，空化器相對于重心的位置為lc，直接側向力作用點相對于重心的位置為lf，且分別為：

與全包裹超空泡航行體的情況類似，作用在空化器上的升力及阻力：

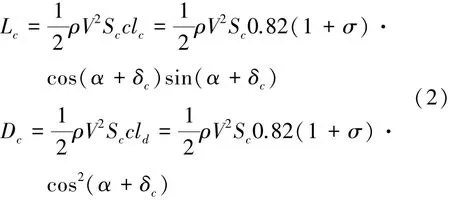
式中，ρ為海水密度，Sc為空化器的最大橫截面積［10-11］。

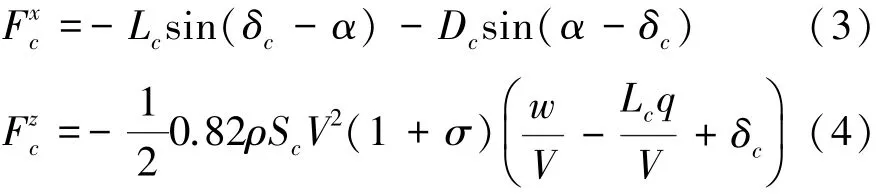
當空化器發生偏轉時，將作用在空化器上的流體動力分解為體坐標系各軸方向的分力［8］為：若記體坐標系下，空化器的坐標為(xc，0)，則空化器上的升力相對航行體重心的轉動力矩［18］為：

尾部壓差主要來自機動時，因與水接觸的角度及截面積不同而造成的，這里近似以尾舵的計算公式來計算：

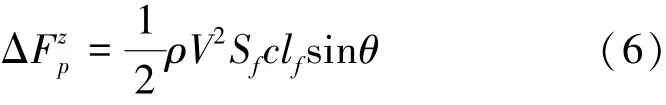
式中，Sf為受力面的最大橫截面積，clf為升力系數。需要注意的是，此處的壓差不同于全包裹超空泡中的尾部滑行力，滑行力是指因航行體尾部部分伸出空泡，與水接觸，而其另一側仍在空泡中時受到的一種流體動力。本文所討論的尾部壓差來源于直接側向力作用時，全部侵入水中的航行體尾部所受到的流體動力。

因航行體在超空泡航行狀態下，速度較高，機動時間較短，故可在小時間范圍內忽略其速度變化，認為速度是恒定的［12］，推力和阻力保持平衡，可以得到下面的二維縱向動力學方程：

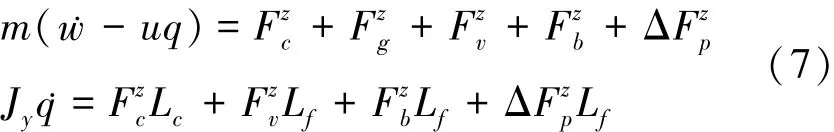
選取深度z，縱向線速度w，俯仰角θ，縱向角速度q為狀態向量，空化器偏轉角δc及直接側向力Fv作為系統輸入，另考慮縱向的2個運動方程［13］：

可得關于縱平面內線性化的狀態方程：

2　模型開環特性驗證

對已建立的非全包裹超空泡航行體系統模型進行開環系統零輸入狀態響應仿真分析，航行體縱向模型系統參數［5，8，12，15］分別為：重力加速度g＝9.81 m/s2，空化器半徑r＝0.019 m，航行體半徑R＝0.05 m，航行體總長L＝1.8 m，航行體速度V＝70 m/s，空化數σ＝0.03，航行體質量m＝2 kg，轉動慣量Jy＝0.54 kg·m2。

系統初始狀態設為［20 0.1 0 0］T，仿真結果如圖2所示。

圖2　系統零輸入狀態響應

由圖中可以看出，系統在零初始狀態下的系統狀態響應，因空化器無偏角，造成頭部空化器所受升力為零，在重力作用下，在2 s附近迅速發散。俯仰角的變化劇烈，在1.9 s以后w和θ幅值急劇震蕩并最終發散，無法實現穩定航行。實際應用中，發射該航行體的有效距離較短，其航行速度在超空泡的狀態下相對較高，導致其機動、姿軌控制的調節時間很短，幾乎都是在毫秒級完成姿軌控制［7］，因此必須對航行體的機動施加閉環控制。

3　反演變結構控制器設計

3.1問題描述

非全包裹超空泡航行體的復合控制是一個涉及多參量，多輸入多輸出的復雜控制系統［15］，反演控制的設計方法可以有效簡化問題［11］，但傳統的反演控制方法無法保證魯棒性，通過引入滑模項，可克服干擾，保證控制器的魯棒性［16］。

為簡要說明問題，在不影響理解的情況下將(9)式改寫：

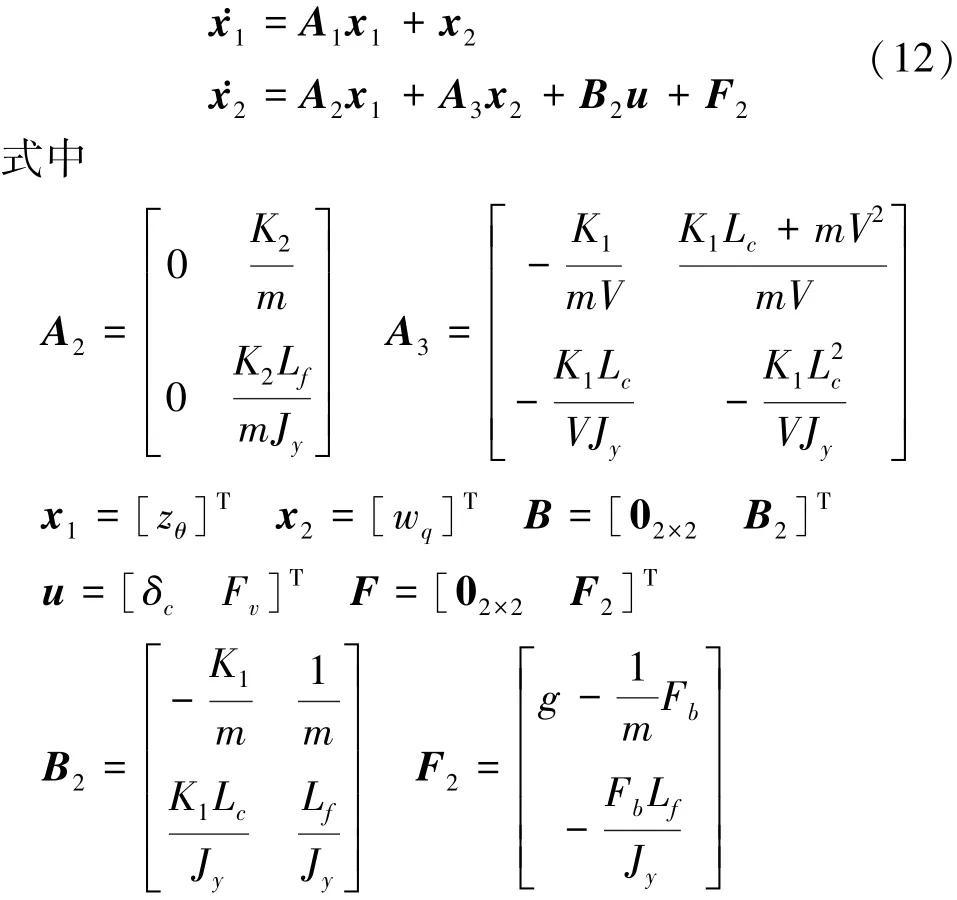
B2非奇異。

3.2控制器設計

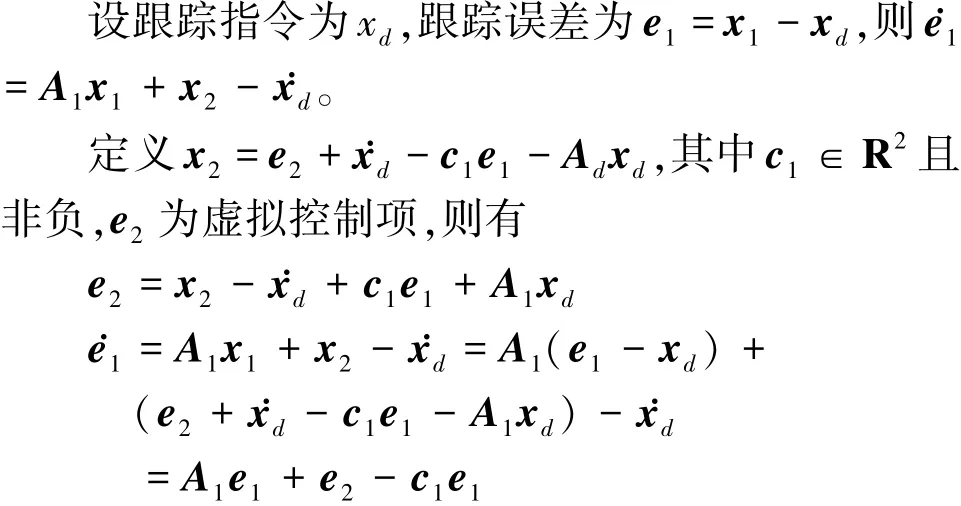
定義一個Lyapunov函數

對V1求導，則有

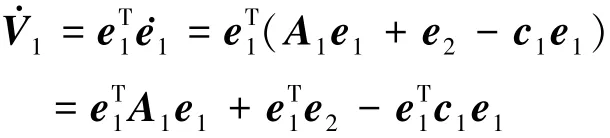
令c1＝A1，由A1各項元素可知，c1滿足非負條件，則上式可進一步化簡為

利用反演思想，設計線性切換面函數

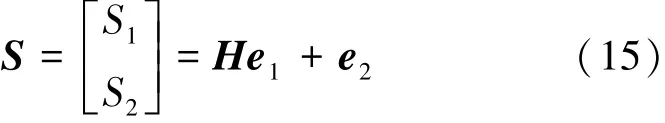
式中，H為滑動模態參數矩陣，且正定。

根據非全包裹超空泡航行體縱向動力學模型可知，只要設計參數使z→0，θ→0，必能保證w→0，q→0，于是有

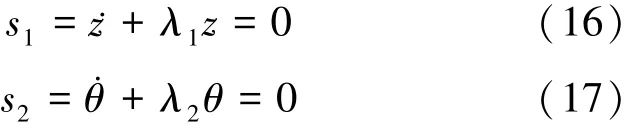
式中，λ1，λ2是保證(16)式、(17)式是Hurwitz的設計參數［10］。綜合(15)～(17)式可進一步得到

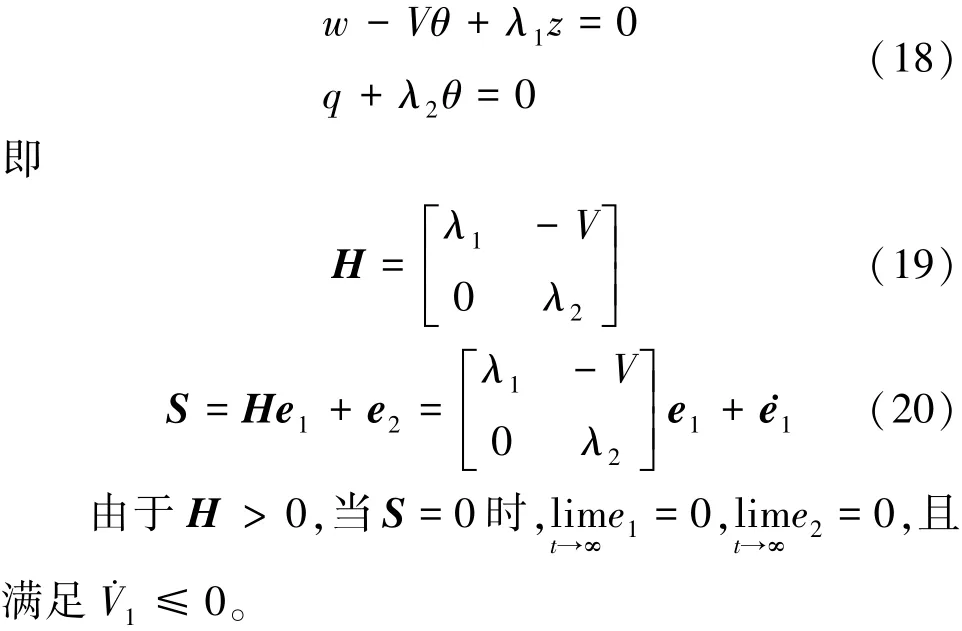
定義第二個Lyapunov函數

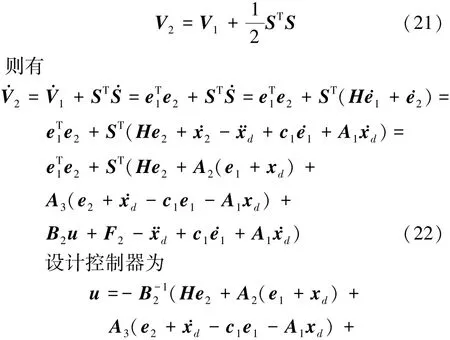
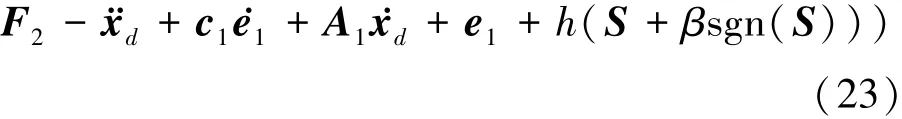
式中，h∈R，β∈R且h＞0，β＞0。

將控制輸入u代入V2中可得

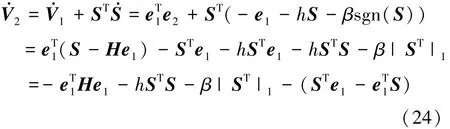
式中，｜ST｜1表示為ST的1范數，且由誤差項e1和切換面函數S維數可知：STe1＝eT1S，因此，上式可整理成

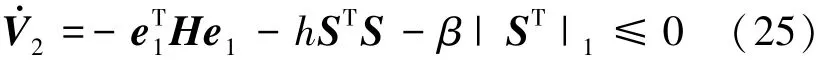
由系統模型(12)可知，參數不隨時間變化，該系統為自治系統，要使V.2＝0成立，當且僅當e1＝e2＝0成立，由LaSalle不變集定理，V2滿足李雅普諾夫定理，系統漸進穩定。由以上推導可知，各個狀態變量在閉環系統基于反演變結構控制器可實現跟蹤控制。

由于控制律(23)是不連續函數，為防止出現抖陣現象，用sat函數代替sgn函數［18］，即

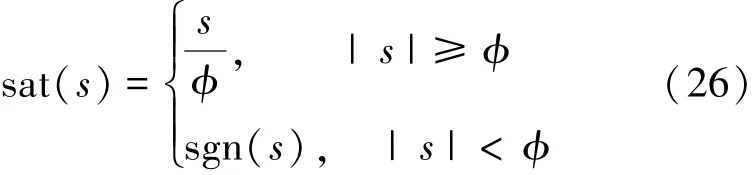
式中，?＝0.1，s∈R。

4　仿真分析

為驗證本文所設計的反演變結構控制器的有效性，對非全包裹超空泡航行體進行跟蹤控制研究。跟蹤控制的仿真驗證主要分兩部分，第一部分是深度z及俯仰角θ均為恒值的定深跟蹤控制，第二部分將深度z的設定信號設置為正弦曲線，考慮驗證控制算法的正弦跟蹤控制效果，設計控制參數為h＝5，β＝0.01，λ1＝λ2＝1。

4.1定深跟蹤控制

設定的航行深度為45 m，深度初始值為30 m，俯仰角設定值為0 rad，初始值為0.1 rad，并與單一變結構策略控制效果進行比較，如圖3至圖5所示。

由圖3和圖4可知，在控制輸入(23)的作用下，各狀態變量均能快速收斂。與單一變結構控制相比，反演變結構控制在各狀態量及誤差等方面的超調量較小，所引起的波動也更小，雖然初始階段的響應速度稍慢于變結構控制，但兩者各狀態量收斂到穩定值的時間是相同的。圖5表示系統狀態變量的跟蹤誤差，可以看出，反演變結構的誤差超調要小于變結構控制，反演變結構控制下的系統性能更優。

圖3　定值跟蹤控制狀態響應

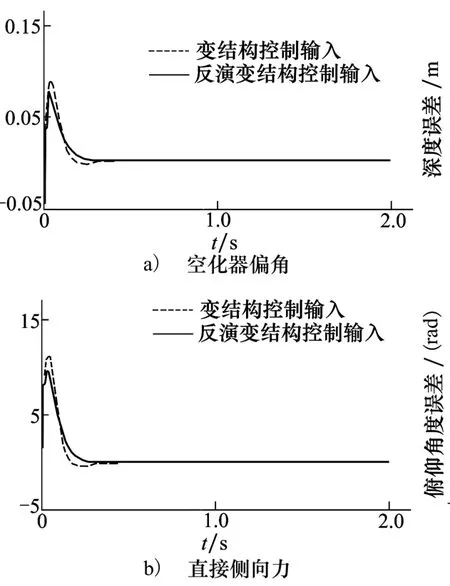
圖4　定值跟蹤控制輸入

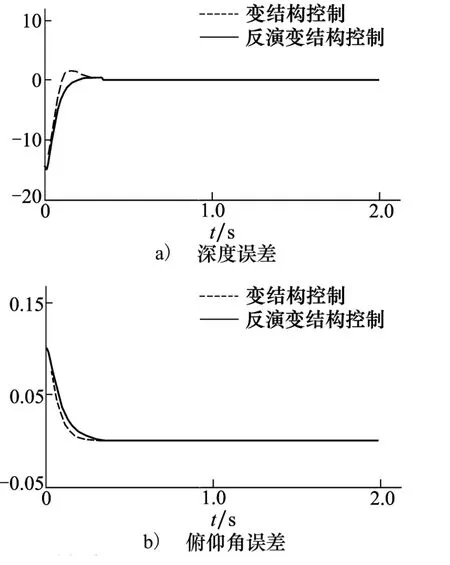
圖5　定值跟蹤控制誤差曲線

4.2正弦跟蹤控制

考慮如下的跟蹤控制信號：設定的深度值為正弦曲線，根據(27)式將俯仰角設為關于深度設定值一階偏導的函數［3］。仿真結果如圖6至圖8所示。

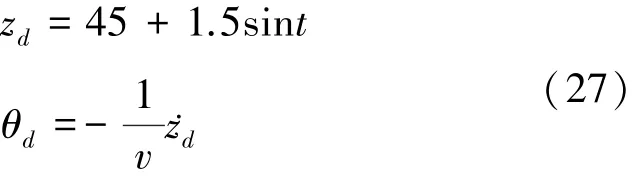
圖6　正弦跟蹤控制狀態響應

圖7　正弦跟蹤控制輸入

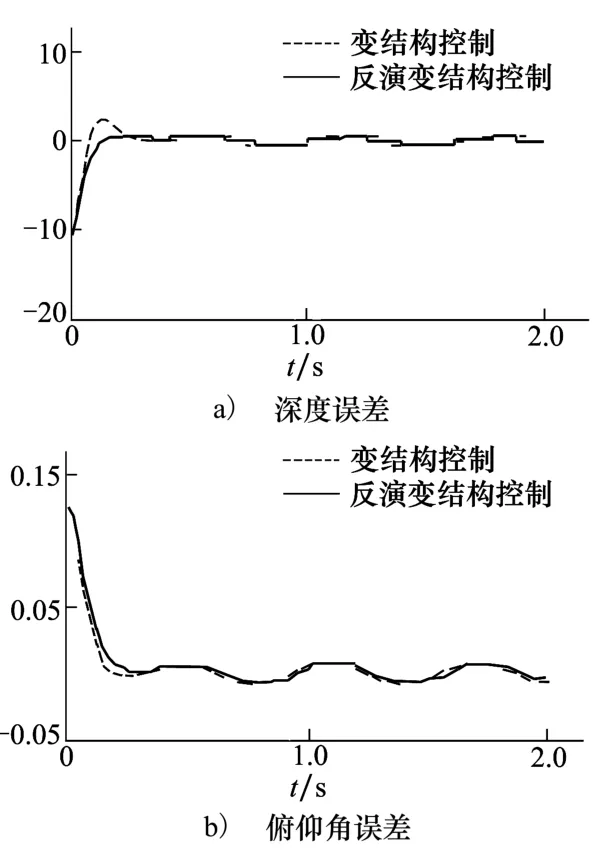
圖8　正弦跟蹤控制誤差曲線

圖6表示的是在正弦信號設定下的系統各參量響應曲線，可以看出，深度z及俯仰角都能夠很好跟蹤設定曲線，并且通過調整變結構控制中趨近律參數進一步削弱抖振。反演變結構與單一變結構在正弦跟蹤控制效果上的區別與定值跟蹤控制效果區別類似，與變結構控制方法相比，反演變結構的超調量更小，跟蹤誤差更快收斂到零。圖7表示的是控制輸入的曲線，明顯可以看出兩者雖然同時收斂，但反演變結構方法的2個控制輸入均小于單一變結構方法，波動也更小。圖8反映了類似的現象，單一變結構的超調較大，容易產生抖動，造成累積誤差較大。

綜上仿真結果不難看出，本文針對非全包裹超空泡航行體所設計的反演變結構控制器具有良好的控制效果，具有超調量小，抑制抖動，調節時間短，作用下的系統性能更優等特點。

5　結 論

本文針對非全包裹超空泡航行體的控制問題，構建了非全包裹超空泡的動力學模型，并據此設計了反演變結構控制器。通過分別對定值跟蹤及正弦跟蹤控制仿真分析證明，該控制器具有較好的控制效果，且與單一變結構控制器相比，其超調量更小，收斂速度更快。研究內容可用于超空泡航行體及類似復合控制航行體的姿軌控制問題。

［1］ Vanek B，Bokor J，Balas G J，et al.Longitudinal Motioncontrol of a High-Speed Supercavitation Vehicle［J］.Journal of Vibration and Control，2007，13(2)：159-184

［2］ Dzielski J E.Longitudinal Stability of a Supercavitating Vehicle［J］.IEEE Journal of Oceanic Engineering，2011，36(4)：562-570

［3］ Mao X，Wang Q.Adaptive Control Design for a Supercavitating Vehicle Model Based on Fin Force Parameter Estimation［J］. Journal of Vibration and Control，2013，1：2-4

［4］ Kirschner I N，Kring D C，Stokes A W，et al.Control Strategies for Supercavitating Vehicles［J］.Journal of Vibration and Control，2002，8(2)：219-242

［5］ Yu K，Zhang G，Zhou J，et al.Numerical Study of the Pitching Motions of Supercavitating Vehicles［J］.Journal of Hydrodynamics，Ser B，2012，24(6)：951-958

［6］ Kirschner I N，Uhlman J S，Perkins J B.Overview of High-Speed Supercavitating Vehicle Control［C］//Proceedings of the AIAA Guidance，Navigation，and Control Conference and Exhibit，2006：3100-3116

［7］ Li D，Luo K，Huang C，et al.Dynamics Model and Control of High-Speed Supercavitating Vehicles Incorporated with Time-Delay［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2014，15(3)：221-230

［8］ Mokhtarzadeh H，Balas G，Arndt R.Effect of Cavitator on Supercavitating Vehicle Dynamics［J］.IEEE Journal of Oceanic Engineering，2012，37(2)：156-165

［9］ Kim S，Kim N.Neural Network-Based Adaptive Control for a Supercavitating Vehicle in Transition Phase［J］.Journal of Marine Science and Technology，2015，20(3)：454-466

［10］Vanek B，Balas G J，Arndt R E A.Linear，Parameter-Varying Control of a Supercavitating Vehicle［J］.Control Engineering Practice，2010，18(9)：1003-1012

［11］Qu Y B，Zhang J Y，Wu Y，et al.An Improved Sliding-Backstepping Control Law for Large Flexible Satellite Attitude Maneuver［C］//2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics，2010：918-923

［12］Mao X，Wang Q.Nonlinear Control Design for a Supercavitating Vehicle［J］.IEEE Trans on Control Systems Technology，2009， 17(4)：816-832

［13］Mao X，Wang Q.Delay-Dependent Control Design for a Time-Delay Supercavitating Vehicle Model［J］.Journal of Vibration and Control，2011，17(3)：431-448

［14］Vanek B，Bokor J，Balas G.Theoretical Aspects of High-Speed Supercavitation Vehicle Control［C］//American Control Conference IEEE，2006：5263-5267

［15］Kirschner I N，Rosenthal B J，Uhlman J S.Simplified Dynamical Systems Analysis of Supercavitating High-Speed Bodies［C］//Proceedings of the 5th International Symposium on Cavitation，2003：1-4

［16］Xia Y，Lu K，Zhu Z，et al.Adaptive Back-Stepping Sliding Mode Attitude Control of Missile Systems［J］.International Journal of Robust and Nonlinear Control，2013，23(15)：1699-1717

Modeling and BackstePPing Variable Structure Control for a IncomPlete-EncaPsulated SuPercavitating Vehicle

Li Yang，Lui Mingyong，Zhang Xiaojian，Peng Xingguang
(College of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China)

The special navigation environment of supercavitating vehicle causes it to be sensitive to disturbance and the dynamics system is highly nonlinear with multivariable coupling；these make it very difficult to design the control system.According to this problem，we study the control system for an incomplete-encapsulated supercavitating vehicle，design backstepping variable structure controller based on force analysis，establish the dynamic model， and prove the system stability.Numerical simulations illustrate the effectiveness of the proposed control method.

angular velocity，backstepping，cavitation，closed loop control systems，computer simulation，controllers，design，dynamics，efficiency，errors，Lyapunov function，mathematical models，matrix algebra， navigation，stability，variable structure control；incomplete-encapsulated，supercavitating vehicle， backstepping variable structure control

TP273

A

1000-2758(2016)02-0215-07

2015-10-20基金項目：國家自然科學基金(51379176、61473233、51109179)資助

李洋(1987—)，西北工業大學博士研究生，主要從事超空泡航行體姿軌控制研究。