光伏并網逆變器非線性離散最速誤差反饋控制策略

張國月 齊冬蓮 張建良 吳 越

?

光伏并網逆變器非線性離散最速誤差反饋控制策略

張國月 齊冬蓮 張建良 吳 越

（浙江大學電氣工程學院 杭州 310027）

基于LC濾波器的光伏并網逆變器輸出電流通常采用dq或ab坐標系下的線性控制策略，難以克服內外擾動等不確定因素對系統的不利影響，因而系統魯棒性較差。在重新建立光伏并網逆變器非線性數學模型的基礎上，提出一種基于非線性離散最速函數的控制策略，通過誤差反饋實現逆變器輸出電流的快速無差跟蹤，提高系統抗干擾能力。搭建以TI公司DSP2812為控制核心的4.5kW三相光伏并網逆變器樣機，實驗證明了該方法的優越性。

光伏并網逆變器 LC濾波器 非線性控制離散最速函數 誤差反饋

0 引言

能源危機和環境污染的加劇，迫使世界各國尋求各種可再生清潔能源作為傳統化石燃料的替代能源。近年來，隨著可再生能源利用技術的不斷完善及應用規模的持續擴大，太陽能正從補充能源向替代能源過渡，已使得光伏并網發電技術的研究成為學術界日益關注的焦點[1]。

作為光伏并網發電系統與電網的接口設備——光伏并網逆變器（Photovoltaic Grid-Connected Inverter, PVGCI）承擔著電能傳遞、控制和轉換的重要功能，其控制策略的優劣直接決定著系統輸出電能能否安全、優質和友好的并網[2]。

在光伏并網發電系統實際運行中，由于需要對光伏陣列進行實時的最大功率點跟蹤[3]，因而要求PVGCI必須具有快速的動態響應特性。此外，隨著分布式光伏發電系統在配電網中滲透率的不斷增大，各國均制定了嚴格的PVGCI并網標準，對系統魯棒性及電能質量提出了嚴格的要求。并網逆變器的數學模型具有明顯的非線性特征，但目前對其控制大多采用小偏差線性化方法，這種方案雖可利用經典線性控制理論進行控制器設計，但當系統工作點因光照強度、環境溫度的變化或內部擾動而移動時，則無法保證系統具有較好的控制性能。

PVGCI線性控制方法實現簡單，控制效果能夠滿足一定的工程要求。忽略電阻、電容和電感等元件所固有的非線性特性，利用經典控制理論中的切線法或小偏差法，可得在工程實際中應用最為廣泛的基于傳遞函數的并網逆變器控制策略，主要包括dq坐標系下的PI控制方法[4]、ab坐標系下的PR控制方法[5]以及二者的改進策略[6,7]等。然而，無論哪種方法均無法克服被控對象參數不確定性對系統的影響，導致魯棒性變差。

為優化系統性能，有些研究人員提出通過基于現代控制理論的線性狀態反饋方法實現閉環系統極點的任意配置[8,9]，從而改善光伏并網發電系統的動態特性。然而，狀態反饋方法卻存在三個制約其工程應用的缺點，包括：①如何合理選擇期望的閉環極點以兼顧系統的穩定性和動態性；②描述系統動態特性的狀態變量及其微分信號在大多數工程實際中難以準確測量，導致極點配置出現偏差或無法實現；③在考慮系統時變的擾動時，由于其存在不可測性，將致使極點配置方法難以實現。

在PVGCI控制方法中，無論是基于傳遞函數的經典控制策略還是基于狀態反饋的現代控制策略，均是建立在實際光伏系統近似線性數學模型之上的。該模型無法反映系統的真實工況，很難消除系統中各種不確定性對控制性能的不利影響，因而線性控制方法魯棒性不強。基于此，一些研究學者提出了諸如狀態反饋線性化、滑模控制和無源控制等非線性控制策略，試圖通過重建系統模型，得到能夠反映光伏系統實際工況的非線性數學模型，進而設計相應的魯棒非線性控制律。

反饋線性化控制（Feedback Linearization Control，FLC）是一種理論較為成熟的非線性控制方法。文獻[10,11]給出了FLC控制在PVGCI中的具體應用方法和仿真分析。文獻[12]針對傳統FLC方法計算復雜、不易實現DSP編程的缺點，提出一種簡化的FLC控制方法。該方法通過將PVGCI控制環由內到外逐層化簡（即假設內環傳遞函數為1），簡化了分析和計算的復雜度，同時進行了仿真和實驗驗證。然而，FLC控制需要確定擾動的具體形式，而實際中的擾動構成極其復雜，難以進行精確測量，這限制了反饋線性化在工程中的應用。

滑模控制（Sliding Mode Control，SMC）方法是一種成熟的魯棒控制方法，其通過切換函數將具有不同特性的反饋控制律結合在一起，使控制量處于滑動模態，這不僅可以保持對結構、參數以及外界干擾等不確定因素的魯棒性，而且可以獲得較為滿意的動態性能。文獻[13]在建立PVGCI非線性離散數學模型的基礎上，設計離散積分滑模控制器，同時采用柔性函數法消除滑模抖振現象，提高滑模穩定性。仿真和實驗結果表明，該控制策略具有快速動態響應能力和較強的魯棒性。然而，傳統的SMC方法只能保證系統在滑動模態實現對不確定性的魯棒控制，而在到達階段則不具有魯棒性[14]，即系統魯棒性無法在整個控制過程中得到保證。針對該問題，文獻[15]提出一種單相PVGCI自適應全局動態滑模控制（Adaptive Total SMC，ATSMC）方法。實驗結果表明，在負載突變的情況下，提出的ATSMC方法可以有效提高系統魯棒性。SMC方法魯棒性較強，具有較好的工程應用前景，但是SMC控制性能依賴于滑模面的選取，而滑模面的選取隨機性較大，沒有明確的選取方法。此外，為證明系統在SMC作用下的穩定性，還需要選擇適當的Lyapunov函數，而Lyapunov函數的選取同樣無規則可循。因此，SMC仍有待改進。

無源控制（Passivity-Based Control，PBC）是從能量的角度，基于Lyapunov穩定性理論，研究系統的穩定控制的非線性控制技術。文獻[16,17]證明了三相PVGCI是嚴格無源的，進而將該系統數學模型轉換為EL（euler-lagrange）方程，通過注入阻尼的方法加快系統能量耗散，從而提高系統的收斂速度，仿真結果表明系統具有較好的穩定性。文獻[18]將PVGCI數學模型轉換為端口受控的耗散哈密頓系統標準形式，進而采用互聯和阻尼分配無源控制方法，簡化控制器的設計。仿真和實驗證明該方法可以加快系統收斂速度，提高系統對于階躍擾動的魯棒性。PBC控制理論通過尋求能量函數設計無源控制律，可以實現系統的全局穩定，且無奇異點，因此對系統不確定性及外部擾動有較強的魯棒性。但是，PBC算法運算較為復雜，且當系統實現模型難以明確建立時，控制律的設計難以實現。

除了上述非線性控制方法外，無差拍控制策 略[19,20]等也可以應用于PVGCI控制中，并取得了一定的研究成果。然而，現有的非線性控制方法仍然依賴于逆變器數學模型，當數學模型難于建立時，將會對控制器參數計算產生影響，進而導致控制器設計無法實現。

本文首先介紹光伏并網逆變器控制領域應用和研究較為廣泛的控制策略的原理，分析其存在的缺點；其次，為改善系統動態性能，提高系統魯棒性，提出一種基于非線性離散最速函數的誤差反饋控制策略：隨后利用離散最速控制函數的不變性原理克服系統模型和內外擾動的不確定性并且通過誤差反饋實現系統動態特性未知和狀態變量難以測量等先驗知識的不足對系統控制器設計的影響。最后通過4.5kW樣機驗證了該方法的有效性和實用性。

1 考慮不確定因素的PVGCI非線性數學模型

1.1 主電路拓撲

圖1為三相光伏并網發電系統的拓撲結構，由直流母線分裂電容1、2，12個IGBT開關管等組成的二極管鉗位式三電平PVGCI以及LC濾波器構成。

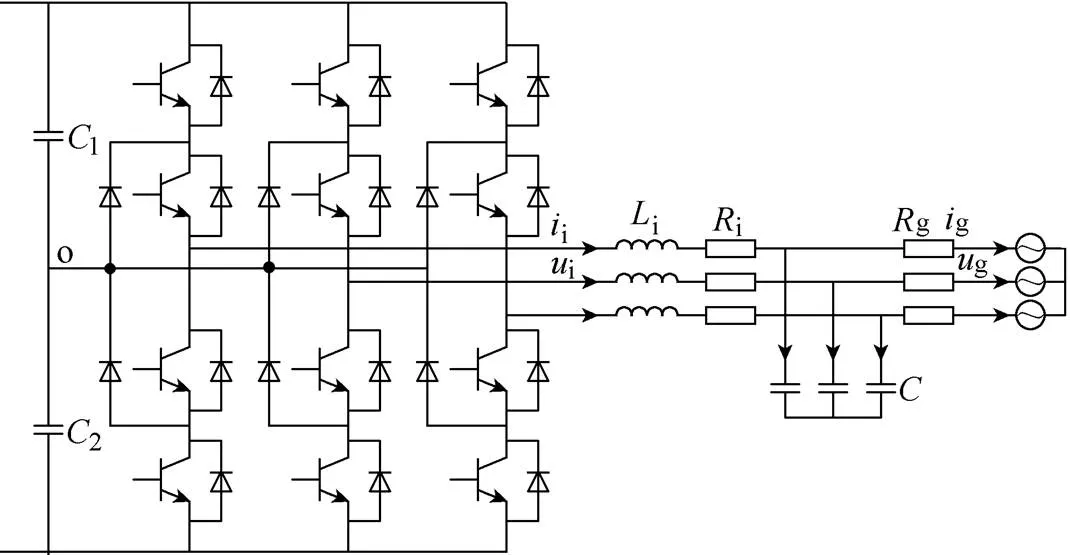
圖1 三相光伏并網發電系統拓撲結構

1.2 PVGCI非線性數學模型

為了簡化分析過程，本文基于三相PVGCI的單相等效電路建立其數學模型，等效電路如圖2所示。圖3為LC濾波器控制結構框圖，根據Mason增益公式可以推導出并網電流g、逆變器輸出電壓i和電網電壓g之間的傳遞函數為

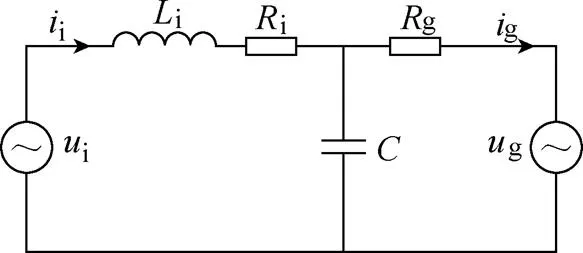
圖2 PVGCI單相等效電路

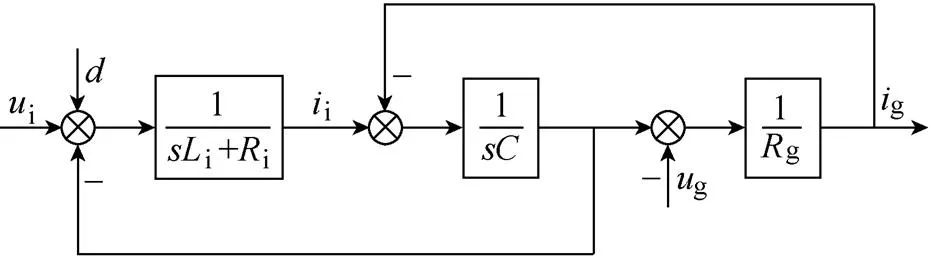
圖3 LC濾波器控制結構框圖

式中，i、i分別為濾波電感及其等效電阻；為濾波電容；g為電網側等效電阻；代表光照強度、溫度突變[21]等系統外部擾動和開關器件老化[22]、調制死區[23]等內部擾動。同時，將電網電壓視作外部電網擾動。并記

式中，為光伏發電系統擾動總和，即PVGCI系統含有的不確定因素。

由式（1）、式（2）可得

其中

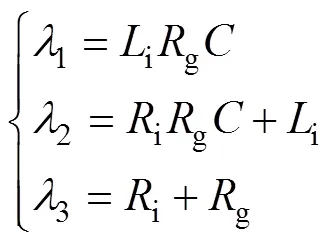
2 理論準備

由以上分析可知，影響系統控制性能的因素主要包括開環動態特性——數學模型(,)、及的不確定性及擾動總和(,,)的復雜時變性。為此，本文通過離散最速控制方法及誤差反饋控制方法尋求上述問題的解決途徑。首先需要根據PVGCI數學模型式（4），推導其對應的誤差反饋控制方法，進而將其與最速控制相結合，從而提高光伏發電系統的魯棒性。

2.1 誤差反饋控制

控制的目的是在系統運行過程中施加適當的控制力，使得被控輸出()快速無差的跟蹤控制目標()，即()()-()→0。

假設

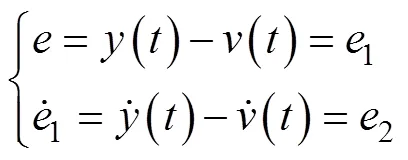
則系統式（5）變為

式中，(1,2,)為變換之后系統的動態特性，(1,2,)=(-1,-2)。定義開環動態在控制過程中的實時表征量為

式中，表征量()是可以由系統的目標值()、控制輸入()和輸出()得到，而這些量往往是已知或可以測量的。此時，若將控制量取為

那么控制系統的微分方程變成

假設式（9）中(1,2)為線性狀態反饋，即(1,2)12，、為滿足一定條件的任意實數。對任意給定的正定矩陣（此處取為單位矩陣），若存在正定的實對稱矩陣，滿足Lyapunov方程

T

取()為系統的Lyapunov函數，()T，此時=-T，即系統漸近穩定，從而有(1,2)→ (0,0)，即()→()。此時，實對稱矩陣為

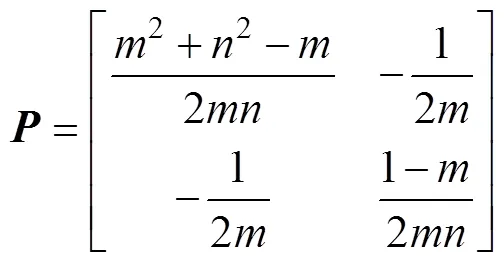
根據Sylvester穩定性判據可知，只需通過選擇適當的＜0、＜0，即可以保證系統穩定。

上述誤差反饋方法能夠克服系統數學模型的不確定性，避免動態特性和狀態變量的難以測量或測量偏差對狀態反饋方法有效性的影響，但當存在擾動總和(,,)時，仍難以實現優良的控制性能。

2.2 離散最速反饋控制

韓京清根據二階積分器串聯型系統的最速控制為Bang-Bang控制的結論，發現以開關曲線為滑動曲線的變結構控制

系統的最速控制函數為

式中，為控制量增益；sgn(·)表示符號函數。同時，為消除系統穩態時的高頻振動并便于工程應用，提出離散系統的最速控制函數形式fhan(1,2,,)。

離散最速控制函數fhan(·)可以抑制具有一定幅值的擾動作用，并使閉環系統以最短時間趨于穩 定[24,25]。

3 離散最速誤差反饋控制方法

3.1 算法設計

本文提出一種基于誤差反饋方法的光伏并網逆變器ab軸電流離散最速誤差反饋控制策略：利用誤差反饋方法消除狀態變量和動態模型的難以測量以及測量器件的精度對控制性能的不利影響；通過最速控制函數抑制系統擾動總和，提高系統魯棒性。此時，光伏并網逆變器電流環離散誤差數學模型為

且有

結合前文分析，同時為實現逆變器輸出電流的無超調跟蹤，本文選取離散最速誤差控制函數為fhan(1,2,,1)

其中

式中，1為快速因子；為阻尼因子。

鑒于光伏并網逆變器dq旋轉坐標系中的電流控制路徑的耦合及存在復雜坐標變換等原因，本文選擇ab靜止坐標系中的控制策略，其中a軸控制框圖如圖4所示（b軸與其相似）。

圖4 光伏并網逆變器離散最速誤差反饋控制框圖

圖4中，LTD表示離散變量的線性微分器，其數據的合理性和可用性參見文獻[24]。

由圖4可見，基于LC濾波器的光伏并網逆變器采用雙閉環控制結構。本文方法與其他方法的區別在于：在電流控制環中，將a軸和b軸的電流參考值a、b與實際輸出a、b之差1()經離散化處理，得到離散誤差變量1()，將1()經過離散求導單元，得到1()微分信號的離散形式2()，將1()、2()送入離散最速控制函數fhan(·)可得光伏并網逆變器控制量a、b。由此可見，本文提出的方法不依賴于精確的數學模型，只需計算參考值與實際值的差值，并將其輸入具有可移植特性的控制器fhan，即可實現光伏并網發電系統輸出電流的有效控制。

3.2 參數選取

由式（12）、式（15）可知，、1為本文涉及的待調參數，而整定這些參數卻沒有理論依據，實際上這也正是fhan(·)的優勢，其在實際應用中不受具體被控對象的限制，可以用同一組參數控制不同的對象，無論不確定因素具體的形式如何，只要其滿足||＜，最速控制函數就可以使閉環系統穩定收斂[26]。

因此，本文按照經驗方法，將1/1設計為PID的比例系數（1一般取為的整數倍），設計為PID的微分增系數（一般有0＜＜2），但并非完全對應，需要通過實驗進一步優化，從而確定最終的參數[27]。

4 實驗結果

為驗證本文提出的光伏并網逆變器非線性離散最速誤差反饋控制方法，搭建了以TI公司DSP2812為控制核心的額定功率為4.5kW三相二極管鉗位式三電平PVGCI樣機，利用可編程直流電源模擬光伏陣列，通過示波器和功率分析儀對逆變器輸出電流進行分析，分別在正常運行、輸入功率突變、突加隨機擾動、系統起動及老化運行五種工況下比較離散最速誤差反饋控制方法和工程中常見的雙閉環PI控制方法的控制性能，實驗波形如圖5、圖6所示，實驗參數見表1。

表1 光伏并網發電系統相關參數

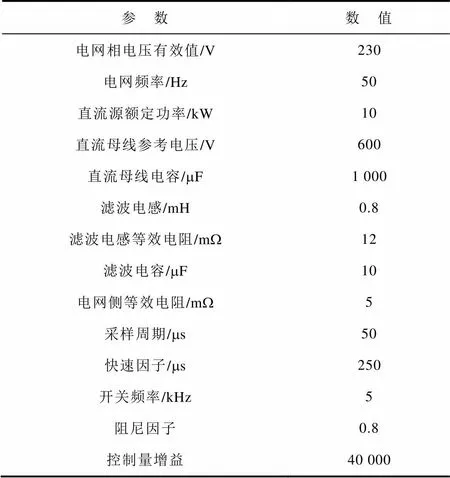
Tab.1 The parameters for the PV grid-connected power system

圖5為光照穩定、無外加擾動和室溫條件下，系統額定功率運行時輸出電壓、電流波形。由圖5可見，與PI控制策略相比（THD＞3%），采用本文提出的非線性離散最速誤差反饋控制策略，在保證電能以單位功率因數并網的同時，可以顯著提高電流波形質量，減小輸出電流總諧波畸變THD＜2%。這主要是因為系統中所存在的諧波可被視為功率器件不平衡、老化、調制死區及電網電壓諧波等擾動在系統中的作用，本文提出的算法恰好具有能夠抑制具有一定幅度限制擾動的能力，因此可以達到優化電能質量，提高系統穩態性能的效果。

圖6所示為光照強度突然減弱和增強時（通過控制直流電源輸出功率進行模擬）逆變器直流側輸入電流與交流側輸出電流的動態變化過程。由圖6可見，當光強突變時，離散最速誤差反饋會使系統在5～7個周期內過渡至新的穩態，同時可以明顯抑制切換瞬間的電流沖擊，使直流側、交流側電流平穩的過渡至穩態，有效地減小了過渡過程的沖擊現象；而PI控制無論是在過渡過程還是在切換瞬間，其控制性能明顯弱于本文方法。可見，本文提出的控制方法可以大幅度提高系統的動態性能，抵抗外部環境因素對光伏發電系統的擾動作用，保證系統安全可靠運行。

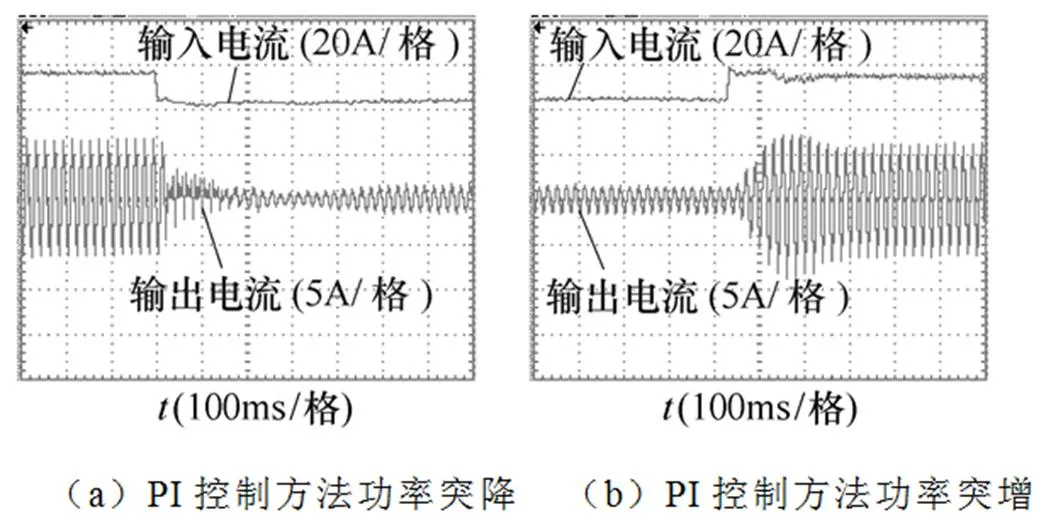
圖7為突加一定幅值范圍的隨機擾動d0.3sgn(sin1)+0.52（利用DSP編程實現，并通過LCD顯示屏觸發，擾動作用時間為100ms）時，光伏發電系統輸出電流波形。如圖7虛線所示，離散最速誤差反饋控制下的逆變器輸出電流僅在突加擾動時產生幅值較小的波動并很快恢復穩態；而PI控制下的電流波形則會出現明顯的畸變，且在擾動消失后仍需一段時間才可恢復穩定。由此可見，本文提出的方法可以提高系統的魯棒性，增強系統抵御擾動的能力。

圖8為逆變器直流側輸入電流和交流側輸出電流的起動波形。由圖8可見，PI控制下逆變器在起動過程中輸出電能存在明顯的波動，且輸入電能抖動劇烈；而本文采用的控制方法可以保證起動過程中電能平滑過渡，無畸變現象發生。可見，本文提出的方法較傳統PI方法能夠明顯提高光伏系統的穩定性。

圖9為光伏逆變器老化實驗波形，老化房環境參數：溫度45℃，濕度40%。隨著逆變器運行時間的變長，其內部器件逐漸老化，故而其非線性特性更加明顯。由實驗截圖可見，傳統PI控制方法下，逆變器輸出電能穩定性較差，而且會出現多次跳機重連現象，由檢測軟件得到的故障報警信息可以發現，除少數通信故障外，大部分跳機現象原因包括直流母線電壓過高、母線電壓不平衡以及過電流等；而在本文提出的控制策略下，逆變器輸出電能較為穩定，雖然也會出現故障停機重連現象，但是相較PI控制已經得到了明顯改善。可見，本文提出的控制策略可以提高系統的魯棒性，降低系統的非線性對控制性能的影響。

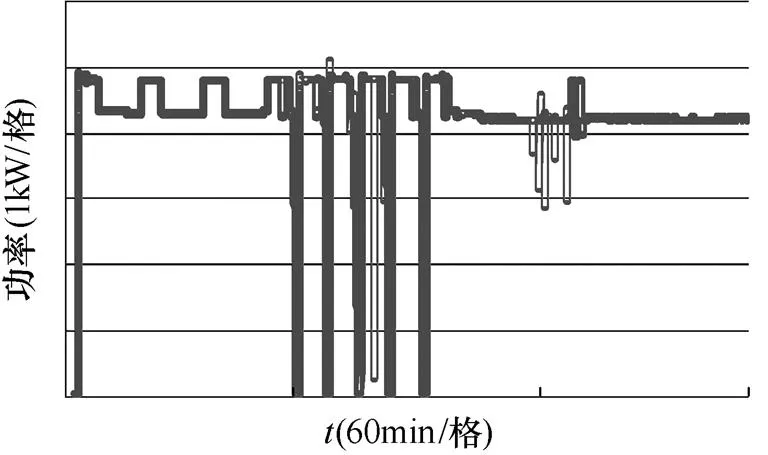
（a）PI控制方法

（b）本文控制方法

圖9 光伏系統老化波形

Fig.9 Aging waveforms of PV system

5 結論

本文提出一種基于離散最速誤差反饋控制策略的光伏并網逆變器非線性方法。該方法可以提高系統的魯棒性，優化系統的綜合性能，使光伏發電系統的整機性能及供電可靠性得到非常明顯的改善。實驗表明，本文所提出的光伏并網發電系統控制策略有效提高了系統的魯棒性，同時改善了動態性能。

參考文獻

[1] 周念成, 樓曉軒, 王強鋼, 等. 電網電壓不平衡下三相光伏發電系統的諧波電流抑制[J]. 電工技術學報, 2015, 30(16): 246-254.

Zhou Niancheng, Lou Xiaoxuan, Wang Qianggang, et al. Harmonic currents suppression for three-phase photovoltaic power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 246-254.

[2] 趙貴龍, 曹玲玲, 祝龍記. 基于光伏并網逆變系統的改進鎖相環設計[J]. 電力系統保護與控制, 2015, 43(2): 108-112.

Zhao Guilong, Cao Lingling, Zhu Longji. Improved PLL design of PV grid inverter system[J]. Power System Protection and Control, 2015, 43(2): 108-112.

[3] 唐磊, 曾成碧, 苗虹, 等. 基于蒙特卡洛的光伏多峰最大功率跟蹤控制[J]. 電工技術學報, 2015, 30(1): 170-176.

Tang Lei, Zeng Chengbi, Miao Hong, et al. A novel maximum power point tracking scheme for PV systems under partially shaded conditions based on Monte Carlo algorithm[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 170-176.

[4] 王飛, 余世杰, 蘇建徽, 等. 太陽能光伏并網發電系統的研究[J]. 電工技術學報, 2005, 20(5): 72-91.

Wang Fei, Yu Shijie, Su Jianhui, et al. Research on photovoltaic grid-connected power system[J]. Transa- ctions of China Electrotechnical Society, 2005, 20(5): 72-91.

[5] Teodorescu R, Blaabjerg F, Liserre M, et al. Proportional-resonant controllers and filters for grid- connected voltage-source converters[J]. IEEE Transa- ctions on Electric Power Applications, 2006, 153(5): 750-762.

[6] 王禹璽, 劉秦維, 劉偉, 等. 一種加權式并聯型重復控制的研究[J]. 電工技術學報, 2015, 30(8): 127-134.

Wang Yuxi, Liu Qinwei, Liu Wei, et al. Study of weighted parallel-type repetitive control[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(8): 127-134.

[7] 杭麗君, 李賓, 黃龍, 等. 一種可再生能源并網逆變器的多諧振PR電流控制技術[J]. 中國電機工程學報, 2012, 32(12): 51-58.

Hang Lijun, Li Bin, Huang Long, et al. A multi- resonant PR current controller for grid-connected inverters inrenewable energy systems[J]. Proceedings of the CSEE, 2012, 32(12): 51-58.

[8] 劉飛, 查曉明, 周彥, 等. 基于極點配置與重復控制相結合的三相光伏發電系統的并網策略[J]. 電工技術學報, 2008, 23(12): 130-136.

Liu Fei, Zha Xiaoming, Zhou Yan, et al. Research on grid-connected strategy combining pole-assignmentand repetitive control in three-phase photovoltaic system[J]. Transactions of China Electrotechnical Society, 2008, 23(12): 130-136.

[9] Lalili D, Mellit A, Lourci N. State feedback control of a three level grid-connected photovoltaic inverter[C]// the 9th International Multi-Conference on System Signals and Devices, Chemnitz, 2012: 1-6.

[10] 張興, 張崇巍, 曹仁賢. 光伏并網逆變器非線性控制策略的研究[J]. 太陽能學報，2002, 23(6): 770- 773.

Zhang Xing, Zhang Chongwei, Cao Renxian. Study on nonlinear control of PV parallel feed inverter[J]. Acta Energiar Solaris Sinica, 2002, 23(6): 770-773.

[11] Lin Wei, Li Rui. Strategy analysis of photovoltaic grid based on input-output feedback linearization[C]// Proceedings of 2012 Asia-PacificPower and Energy Engineering Conference, Shanghai, 2012: 1-4.

[12] Bao Xianwen, Zhuo Fang, Tian Yuan, et al. Simpli- ?ed feedback linearization control of three-phase photovoltaic inverter with an LCL filter[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2739-2752.

[13] 黃慶義, 段啟迪, 郝翔, 等. 具有精確非線性補償的三相光伏并網逆變器滑模變結構控制策略[J]. 電源學報, 2013, 4(4): 81-87.

Huang Qingyi, Duan Qidi, Hao Xiang, et al. A discrete-time integral sliding-mode controller with nonlinearity compensation for three-phase grid- connected photovoltaic inverter[J]. Journal of Power Supply, 2013, 4(4): 81-87.

[14] Wai Rongjong, Lin Kuomin. Robust decoupled control of direct field-oriented induction motor drive[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 837-854.

[15] Wai Rongjong, Wang Wenhung. Grid-connected photovoltaic generation system[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2008, 55(3): 953-964.

[16] 王久和, 慕小斌. 基于無源性的光伏并網逆變器電流控制[J]. 電工技術學報, 2012, 27(11): 176-182.

Wang Jiuhe, Mu Xiaobin. Current control strategy of photovoltaic grid-connected inverter based on passivity[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 176-182.

[17] Mu Kun, Ma Xiaoyu, Mu Xiaobin, et al. A new nonlinear control strategy for three-phase photo- voltaic grid-connected inverter[C]//Proceedings of IEEE International Conference on Electronic and Mechanical Engineering and Information Technology, Harbin, 2011, 9: 4611-4614.

[18] Chen Zongxiang, Ge Lusheng. Research on current control strategy for grid-connected inverter based on passivity-based control[C]//Proceedings of IEEE Inter- national Conference on Energy Conversion Congress and Exposition, Atlanta, GA, 2010: 79-83.

[19] 高金輝, 邢倩. 無差拍控制的非隔離型并網逆變器漏電流分析[J]. 電力系統保護與控制, 2014, 42(9): 120-125.

Gao Jinhui, Xing Qian. Deadbeat control for trans- formerless PV grid inverter leakage current analysis[J]. Power System Protection and Control, 2014, 42(9): 120-125.

[20] Fischer J R, González S A, Herrán M A, et al. Calculation-delay tolerant predictive current controller for three-phase inverters[J]. IEEE Transactions on Industrial Electronics, 2014, 10(1): 233-242.

[21] Liu F R，Duan S X，Liu F，et al. A variable step size INC MPPT method for PV system[J]. IEEE Transa- ctions on Industrial Electronics, 2008, 55(7): 2622- 2628.

[22] Kulkarni A, John V. Mitigation of lower harmonics in a grid-connected single-phase PV inverter[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5024-5037.

[23] Herran M A, Fischer J R, Gonzalez S A, et al. Adaptive dead-time compensationfor grid-connected PWM inverters of single-stage PV systems[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2816-2825.

[24] 韓京清. 自抗擾控制技術[M]. 北京: 國防工業出版社, 2009.

[25] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[26] 韓京清. 最速反饋控制的不變性[J]. 系統科學與數學, 2005, 25(4): 498-506.

Han Jingqing. Invariability of time optimal feedback control[J]. Journal of System Science and Mathe- matical Science, 2005, 25(4): 498-506.

[27] 韓京清. 自抗擾控制技術[J]. 前沿科學, 2007, 1(1): 24-31.

Han Jingqing. Active disturbance rejection control[J]. Frontier Science, 2007, 1(1): 24-31.

Control Strategy of Non-Linear Discrete Time-Optimal Error Feedback in PV Grid-Connected Inverter

（College of Electrical Engineering Zhejiang University Hangzhou 310027 China）

The output current control with LC filter of PV grid-connected inverter (PVGCI) usually adopts linear control strategies in dq orabframe. It is difficult to resist adverse effects of uncertain factors produced by internal and external disturbances. As a result, the system has poor robustness. According to the rebuilding of nonlinear mathematical model of PVGCI, a new control method based on nonlinear time-optimal function combined with error feedback is proposed, to realize the rapid tracking of output current without steady state error and enhance the capability of disturbance-rejecting of the whole system. A prototype of three-phase grid-connected PV inverter is designed based on DSP2812. Experiments on this prototype verify the proposed method.

PV grid-connected inverter, LC filter, nonlinear control, non-linear control discrete time-optimal function, error feedback

TM46

張國月 男，1987年生，博士研究生，研究方向為可再生能源發電與微電網。

E-mail: zgytju@163.com

齊冬蓮 女，1973年生，教授，博士生導師，研究方向為非線性控制理論及其在電力系統中的應用、信號分析與處理。

E-mail: qidl@zju.edu.cn（通信作者）

2015-01-05 改稿日期 2015-05-15

國家高技術研究發展計劃（863計劃）（2015AA050402），浙江省自然科學基金（LY15E070001）和中央高校基本科研業務費專項資金（2014QNA4011）資助項目。