基本不等式解題“三步走”
李代輝
(四川省德陽市德陽中學校)
基本不等式解題“三步走”
第一步:應用特征
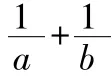
例1.已知a2+b2=1(a,b>0),求a+b的最大值。
分析:條件中有平方和為定值、結論中有和為最值,滿足基本不等式的應用特征,故可以直接使用基本不等式求解。而包含和與平方和的基本不等式是公式④。
例2.α為銳角,求sinαcosα的最大值。
分析:題目中只有一個字母α,但可以發現結論中是sinα與cosα積的最值,而sinα與cosα的平方和是定值1為隱藏條件,滿足基本不等式的應用特征。包含和與積的基本不等式是公式②。
解:∵2sinαcosα≤sin2α+cos2α=1
點評:在使用基本不等式時可能會出現在和、積、倒數、平方和這四個中,題目上只有一個最值。那就需要你尋找隱藏的定值,而隱藏的定值就必然在剩下三個中(例1)。同時在使用中不一定是兩個字母,它可能是只有一個字母(例2)。
第二步:應用技巧
在題目滿足基本不等式的應用特征時,經常會出現不能直接得出定值或直接應用公式的情況。這時就需要有一定的技巧進行轉化,技巧規律為:加減常數(或定值)與乘除常數(或定值)。舉例如下:
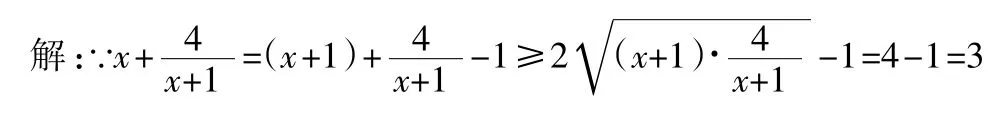
李代輝
(四川省德陽市德陽中學校)
(當且僅當x+1=2時等號成立)
分析:題目中滿足倒數和與和的特征,但基本不等式中沒有對應的公式。此時直接在結論中乘除定值后整理就可以把和與倒數和的特征轉化為和與積的特征,從而使用公式①。
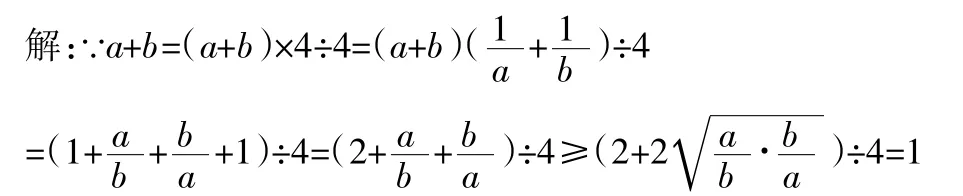
(當且僅當a=b=2時等號成立)
∴a+b的最小值為1。
第三步:應用檢測
基本不等式的應用過程中會全程貫穿應用前提“一正二定三相等”。在前面兩步中,我們主要在公式的應用和定值上下功夫,第三步就需要考慮“一正”和“三相等”了。
“一正”是出現字母為負需要提負調整為正后才能用基本不等式。
“三相等”是指在計算出結果后一定要檢驗其不等式中等號是否能夠成立,如果能成立,則最值是可以取到的;如果不成立,則不能用基本不等式求解,需要放入函數中求解。
∵a+b=1
總結:在實際使用中,按照“三步走”的原則弄懂知識點后,加以少量的訓練鞏固就可以解決所有涉及基本不等式的最值問題,從而達到靈活應用基本不等式的目的。
·編輯李建軍

