壓電微位移臺的動態遲滯建模及實驗驗證

楊曉京，彭蕓浩，李　堯

(昆明理工大學 機電工程學院，云南 昆明 650500)

?

壓電微位移臺的動態遲滯建模及實驗驗證

楊曉京*，彭蕓浩，李堯

(昆明理工大學 機電工程學院，云南 昆明 650500)

為了提高壓電微位移平臺快速定位的精確度，建立了一種表征壓電微位移平臺驅動電壓與輸出位移關系的定位模型。考慮壓電工作臺在快速、大行程精確定位過程中會受壓電陶瓷遲滯特性及本身動態特性的影響，本文采用Bouc-Wen模型描述壓電陶瓷遲滯特性，并結合壓電工作臺的動態特性進行共同建模，使模型同時體現壓電工作臺的動態特性與遲滯特性。為了驗證模型的正確性，搭建了基于壓電微位移平臺和相關驅動器的實驗設備對模型進行了實驗驗證，并進行了測控程序的二次開發。研究結果表明，與單純的Bouc-Wen模型相比，提出模型在最大位移輸出為40 μm，輸入電壓頻率為40 Hz時的最大誤差由3.04 μm下降到了0.67 μm，此時最大相對誤差為1.68%。得到的結果驗證了提出的模型可較好地模擬壓電工作臺的遲滯特性與動態特性，大大提高壓電微位移平臺在快速、大行程定位中的精確度。

壓電微位移臺；動態特性；遲滯特性；Bouc-Wen模型；運動定位

1　引　言

壓電微位移平臺是基于柔性鉸鏈機構，由壓電陶瓷提供驅動力的微位移精密機構。具有分辨率高、無摩擦、響應快和無噪音等優點，被廣泛應用于超精密加工制造、微納定位、生物工程、微機電系統等領域[1]。但是，壓電陶瓷驅動器的輸入電壓與輸出位移之間存在的遲滯非線性，壓電陶瓷驅動器本身具有的蠕變性以及壓電工作臺的動態特性，都會對壓電工作臺的定位準確度造成影響，使其定位精度降低[2]。

為了提高微位移平臺的定位精度，國內外很多專家學者提出了不同的壓電驅動器設計方案[3-5]，同時也對壓電陶瓷微位移器的數學模型進行了大量的研究，建立了Preisach模型[6-7]、Prandtle-Ishlinskii模型[8-9]、Duhem模型[10-11]、Bouc-Wen模型[12-14]等遲滯模型。但是，這些模型均不能表示微位移平臺運動過程的全部信息，大部分模型僅能表示壓電執行器的遲滯性、蠕變性或平臺的動態特性。由于壓電驅動器的蠕變性在平臺的慢速定位中影響顯著，遲滯性在大行程定位中顯示明顯，而平臺快速運動中主要體現動態特性[2]，這就使得在進行大行程、快速定位的時候，微位移平臺的定位精度不高。為了提高平臺的定位精度，就必須將壓電微位移平臺的動態特性和遲滯特性結合起來建模。

本文選取Bouc-Wen模型對平臺的遲滯特性進行數學建模。Bouc-Wen模型是由Bouc[15]于1967年提出，并由Wen[16]于1976年完善的微分方程。該方程由一系列不定參數構成，不同的參數對應于不同的遲滯環。近年來，眾多學者對該模型模擬壓電陶瓷的遲滯性進行了研究[12-14]，取得了一定成果。同時，該模型本身為動態模型，與靜態模型相比，能較好的反應壓電執行器的動態遲滯性，但隨著輸入信號頻率的上升，模型的準確性會逐步下降。為了進一步提高平臺在大行程、較快速度下的定位精度，本文研究了壓電工作臺的線性動態模型，并通過將線性動態模型與遲滯模型相結合，得到了更加精確的動態遲滯模型，使得該模型能夠同時表示壓電微位移平臺的動態特性和遲滯特性。最后，以三維壓電微位移平臺為對象，驗證了由線性動態模型與遲滯模型結合的動態遲滯模型的精確性，并將其與單純基于Bouc-Wen模型建模的結果進行了比較，驗證了模型的優越性。

2　動態遲滯模型

2.1動態遲滯模型的建立過程

壓電微位移平臺主要由壓電驅動器和柔性鉸鏈等組成，其特性主要由壓電驅動器的遲滯性、蠕變性，位移平臺的動態特性來表現。因此，微位移平臺系統為典型的二階系統[17]。當壓電工作臺的工作頻率遠小于其諧振頻率時，可將工作臺系統看做一個彈簧-阻尼系統。其中，彈簧表示壓電驅動器的特性，阻尼表示柔性鉸鏈的特性。則系統的力與位移的關系為：

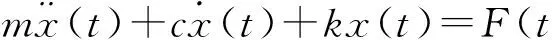
(1)

同時，工作臺的輸出力還與壓電驅動器的輸出力呈遲滯非線性關系：

F(t)=H{V(t)}.

(2)

聯立式(1)、(2)，轉換成標準的二階系統的形式：

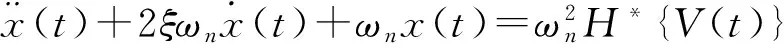
(3)

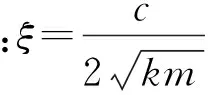
式(3)即為壓電微位移平臺的動態遲滯模型，既體現出了微位移平臺的遲滯特性，又表示出了平臺的動態特性。

2.2Bouc-Wen模型的建立過程

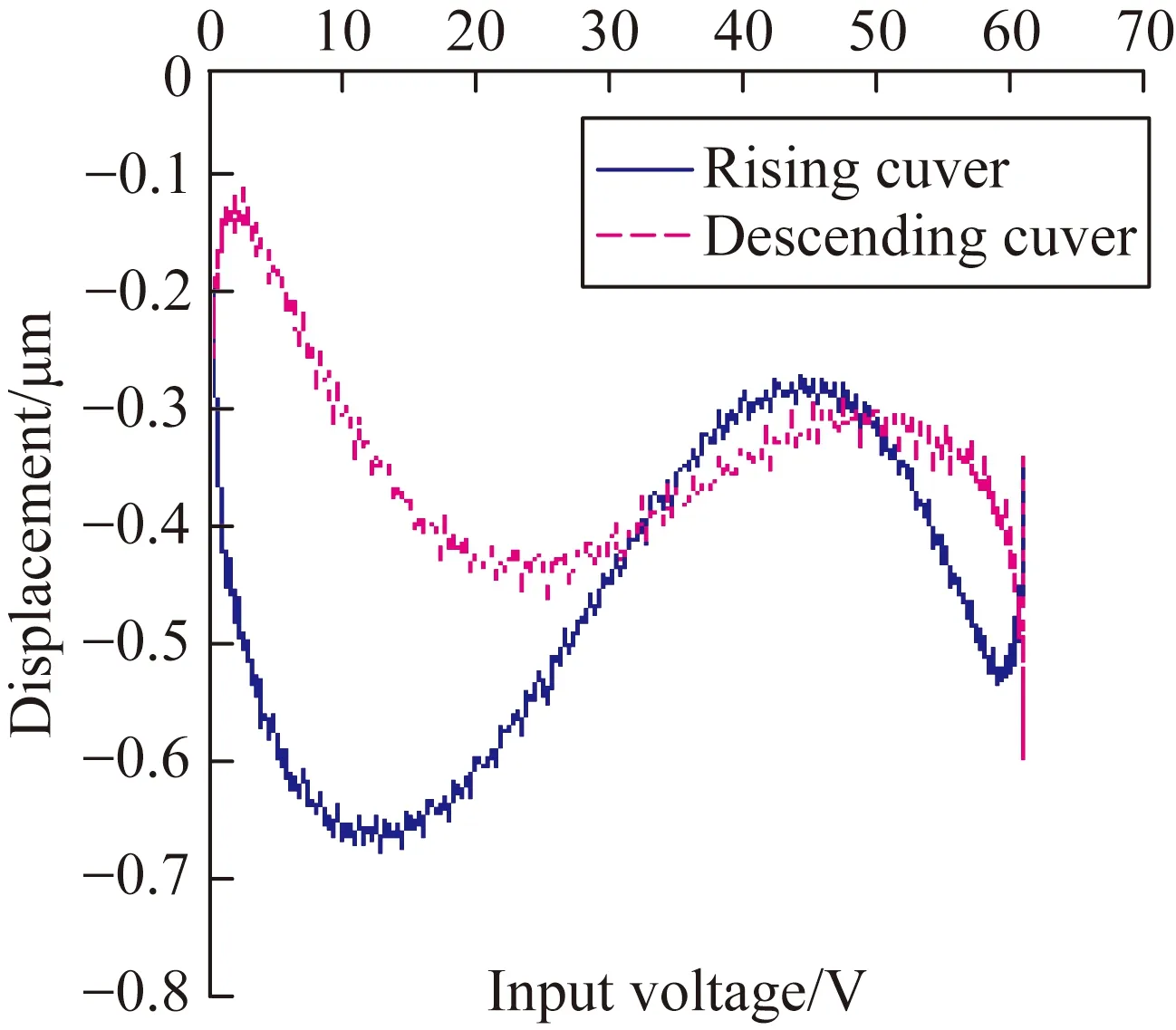
圖1所示為壓電微位移平臺的遲滯曲線。圖中虛線所示為遲滯曲線上位移最大值與最小值的連線。壓電微位移平臺的遲滯曲線即可看成是該直線加上曲線的遲滯分量構成的：

x(t)=kvu(t)+h(t)+x0，

(4)

式中：x(t)為輸出位移，u(t)為輸入電壓，kv為構成輸入電壓與輸出位移線性關系的比例常量，h(t) 為遲滯分量，x0為初始位移。

其中，h(t)的一階導數為[15]：

，

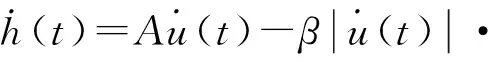
(5)

式中：A、β、γ為待求參數。為了簡化辨識過程，降低辨識難度，通常情況下將n設為1，則有：

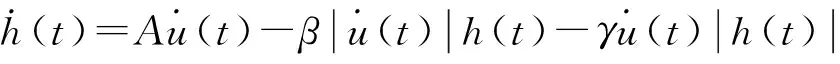
(6)

則只需要確定參數kv，A、β、γ便能得到相應的Bouc-Wen模型。

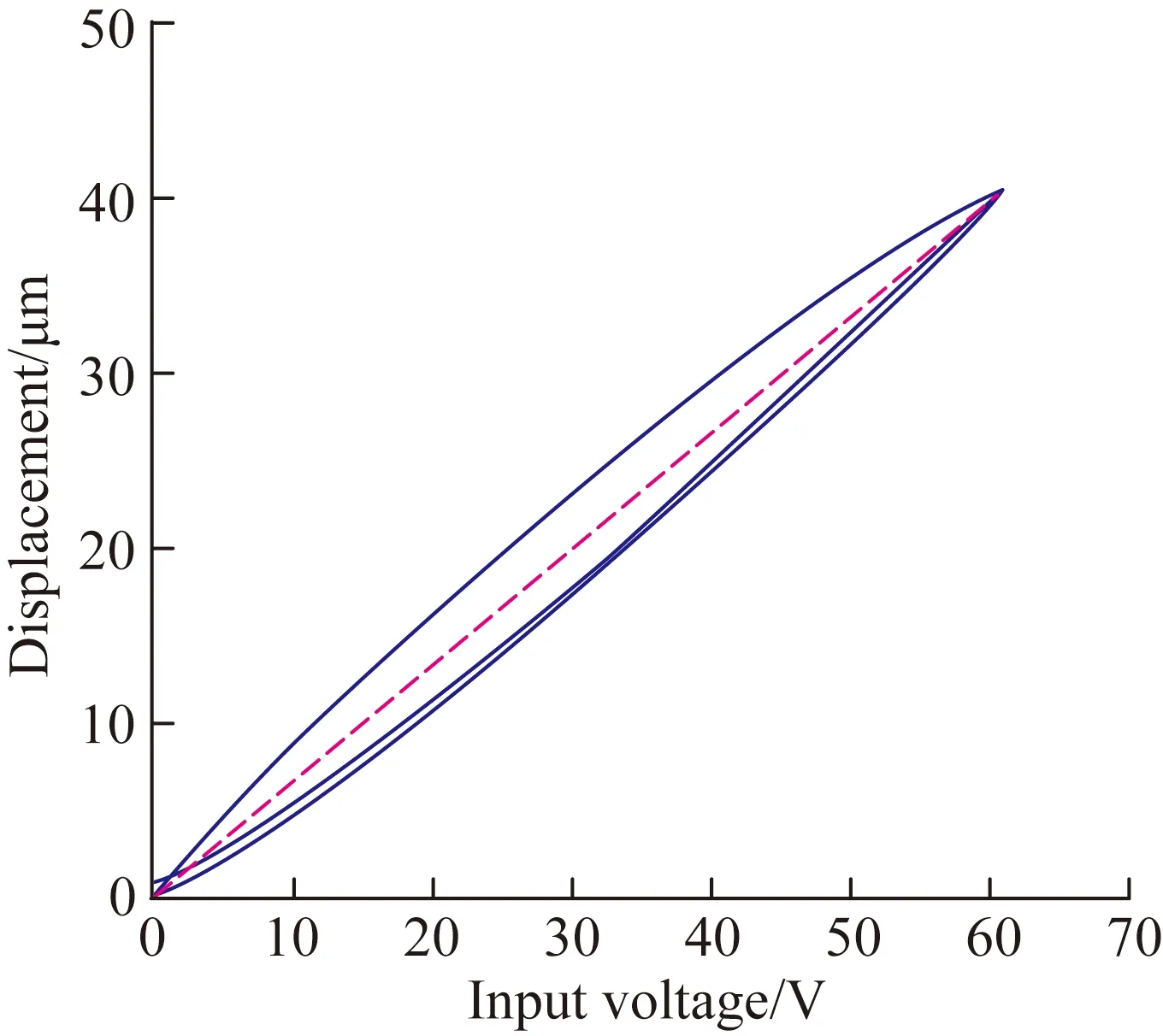
圖1壓電微位移平臺輸入電壓與輸出位移的遲滯曲線

Fig.1Hysteresis curves of input voltage and output displacement of piezoelectric positioning stage

3　模型參數的辨識

壓電微位移平臺的動態遲滯模型由平臺的遲滯特性和動態特性組成，因此，建模也可以分成這兩個部分進行。當壓電平臺進行慢速定位時，平臺的動態特性表現不明顯，平臺主要表現為遲滯特性。則模型方程可簡化為：

x(t)=H*{V(t)}.

(7)

此時，僅需要對系統進行遲滯模型的建立即可。Bouc-Wen模型的參數辨識過程如下：

對壓電微位移平臺輸入兩組電壓u(t)和u′(t)，它們之間的關系為u′(t)=u(t)±c(c為常數)，將其分別代入式(4)，得：

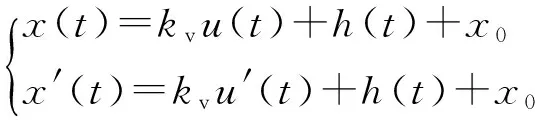
(8)

由式(8)可解得：

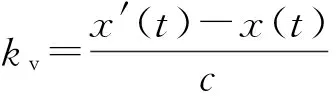
(9)

又對于一個完整的遲滯過程來說，h(t)的變化量為0，則有：

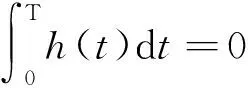
(10)

由式(10)和式(8)，可以確定初始位移x0：

(11)

由式(6)可得：

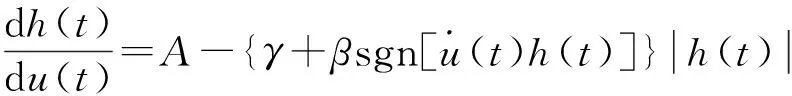
(12)

在圖1中求得直線與遲滯曲線的交點(u0，x0)，由Bouc-Wen模型的性質可知，此時h(t)為0。則由式(8)、(12)可得：

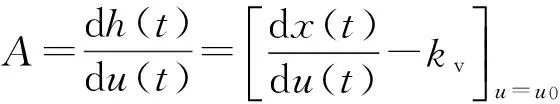
(13)

在上升曲線中，當點(u1，x1)處于(u0，x0)下方時，由式(12)可得：

(14)

同樣，在上升曲線上取點(u2，x2)處于(u0，x0)上方，同理可得：

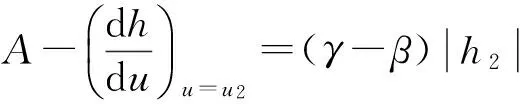
(15)

聯立式(14)、(15)可得：

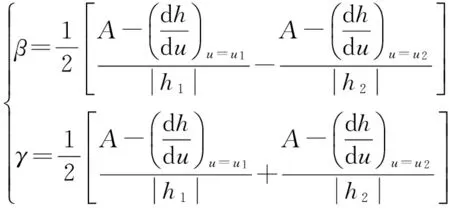
(16)

至此，Bouc-Wen模型的所有參數均求解完成，平臺的遲滯模型也建立完成。當壓電微位移平臺進行小行程快速定位時，平臺的遲滯性表現不明顯。此時，平臺表現線性動態性，則式(3)可寫為：

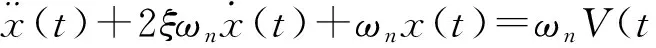
(17)

此時，需要確定的參數為ξ和ωn，可由線性系統的頻率響應辨識法獲得。

4　實驗驗證

4.1實驗裝置

采用如圖2所示的實驗裝置，來完成Bouc-Wen模型和線性動態模型的數據采集和模型的驗證實驗。該實驗裝置采用哈爾濱芯明天科技有限公司生產的三維壓電微位移平臺XP-611.XYZ和XE-500/501 D系列壓電陶瓷控制器搭建組成，并進行了測控程序的二次開發。

以X軸方向為例進行實驗。壓電微位移平臺X軸的基本參數如下：輸入電壓為0～150 V；最大輸出位移為120 μm(±20%)；開環定位分辨率為0.2 nm；重復定位精度為30 nm；空載響應頻率為350 Hz。XE-500/501 D系列壓電陶瓷控制器由放大器模塊、傳感器控制模塊和顯示與接口模塊等組成。實驗過程中，通過壓電陶瓷控制器驅動微位移平臺，并與計算機相連，采用基于LabVIEW的數據采集處理程序，對數據進行采集處理。

圖2　實驗裝置實物圖

4.2Bouc-Wen模型參數辨識

為了得到準確的參數值，先讓壓電微位移平臺輸入一組0.2 Hz，電壓分別為0～61 V、30～91 V，最大位移分別為40 μm、62 μm的正弦信號，如圖3所示。

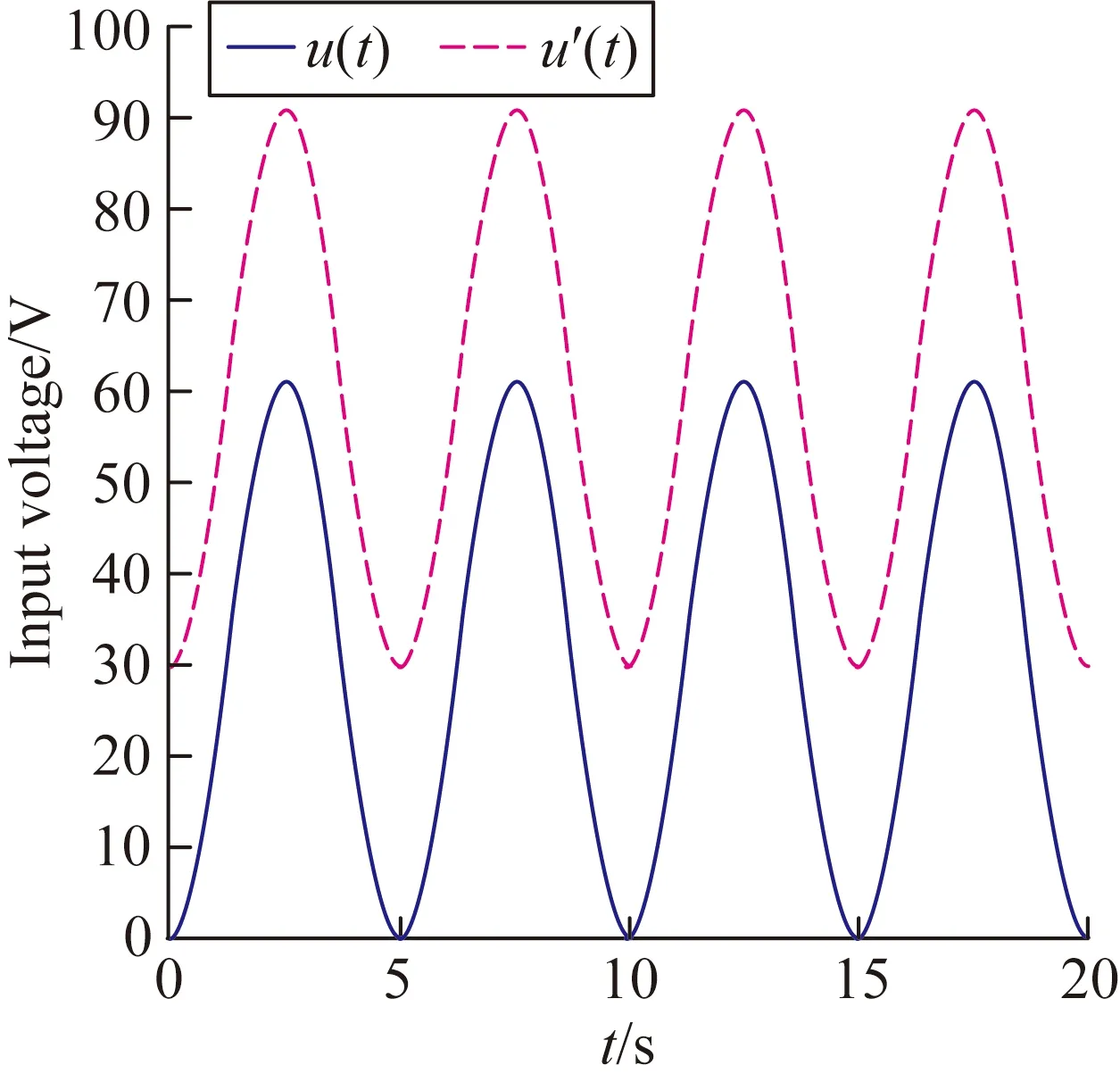
(a)輸入電壓時間曲線

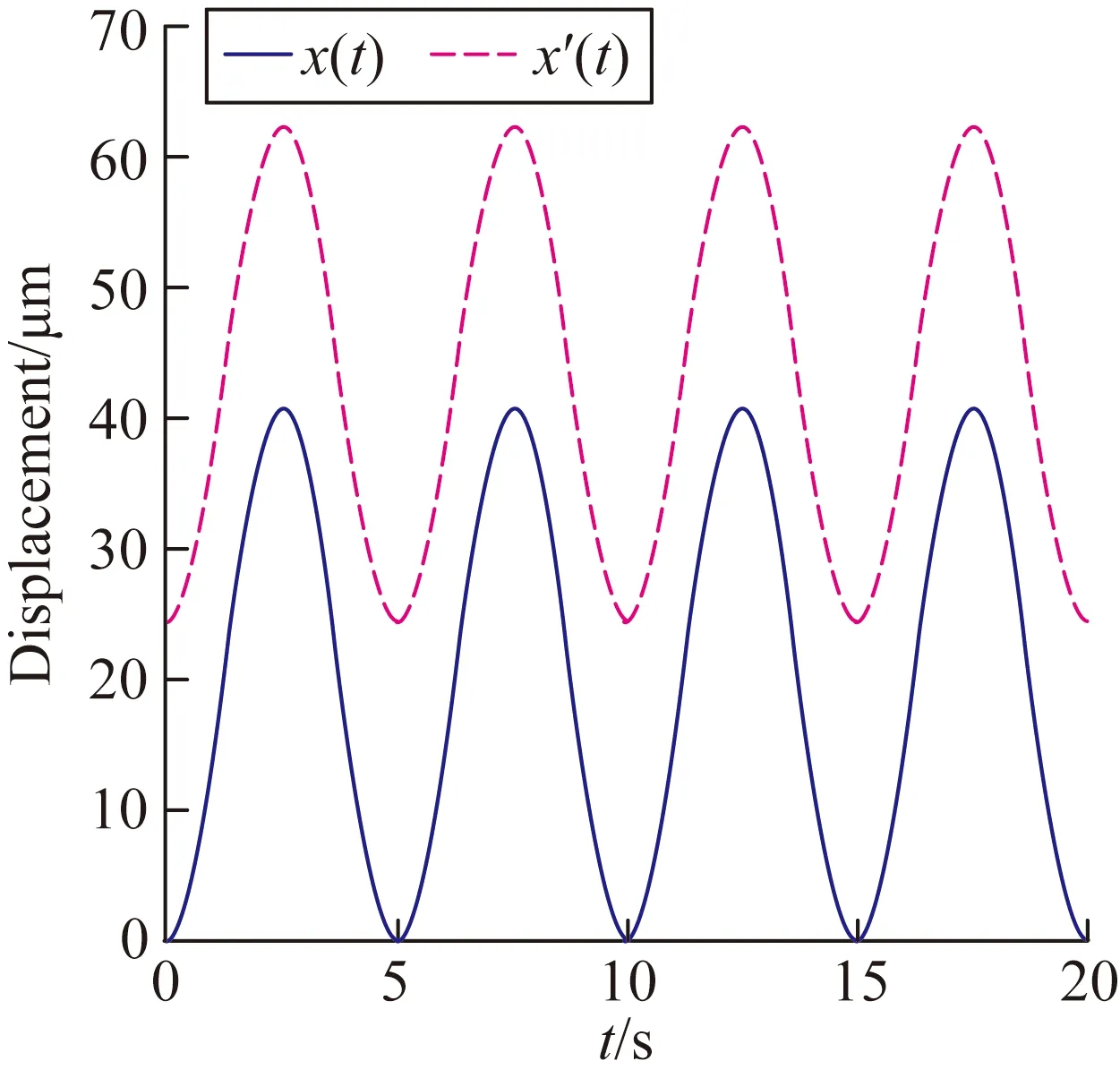
(b)輸出位移時間曲線

由圖3和式(9)、(11)、(13)、(16)可得模型的參數分別為：kv=7.015×10-7，x0=0.354×10-6，A=-1.87×10-7，β=0.085 4，γ=-0.093 5。

再將各參數代入式(4)、(6)，即可求出Bouc-Wen模型的表達式，完成模型的建立。

4.3動態特性的辨識

平臺的動態特性參數由頻域響應法獲取，由于壓電微位移平臺X軸向的空載響應頻率為350 Hz，所以，將輸入電壓信號由0 Hz逐步加至550 Hz，平臺的最大位移控制在6 μm左右。通過MATLAB以二階系統傳遞函數的形式，對實驗數據進行處理。得到的動態特性的參數為：

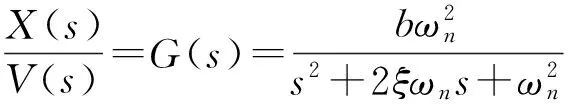
(18)

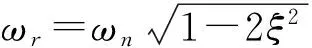
4.4動態遲滯模型的驗證

結合遲滯模型和平臺的動態特性模型，將兩模型代入式(3)中，即可建立平臺的動態遲滯模型。為了驗證模型的準確性，將平臺的輸入電壓信號設置為40 Hz的正弦信號，最大位移定為40 μm，并與單純的Bouc-Wen模型建模進行比較，結果如圖4所示。

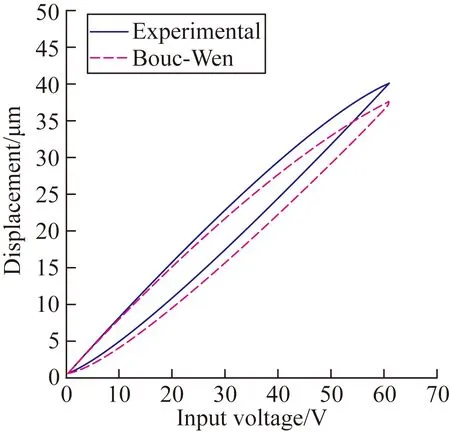
圖4　Bouc-Wen模型與實際遲滯環

圖4所示為單純的Bouc-Wen模型與實際遲滯環的電壓-位移曲線圖。從圖中可以看出，在壓電微位移平臺較快速、大行程定位時，用單純的Bouc-Wen模型進行壓電微位移平臺遲滯模型的描述時，出現了較大的誤差，模型最大誤差出現于最大位移40 μm處，誤差為3.04 μm，且模型較實際遲滯環有向下的偏移，這是由于單純的Bouc-Wen模型沒有考慮到平臺自身的動態特性，因此在平臺快速定位的過程中產生了較大的誤差，且隨著平臺位移的增大，誤差也隨之增大。圖5所示為改進后的動態遲滯模型與實際遲滯環的電壓-位移曲線圖、誤差曲線圖和輸出位移時間曲線圖。由于改進后的動態遲滯模型考慮到了平臺本身的動態特性，在單純的Bouc-Wen模型中加上了平臺的動態特性，所以得到了較好的精度，提高了模型的精確度，最大誤差為0.67 μm，最大相對誤差為1.68%。

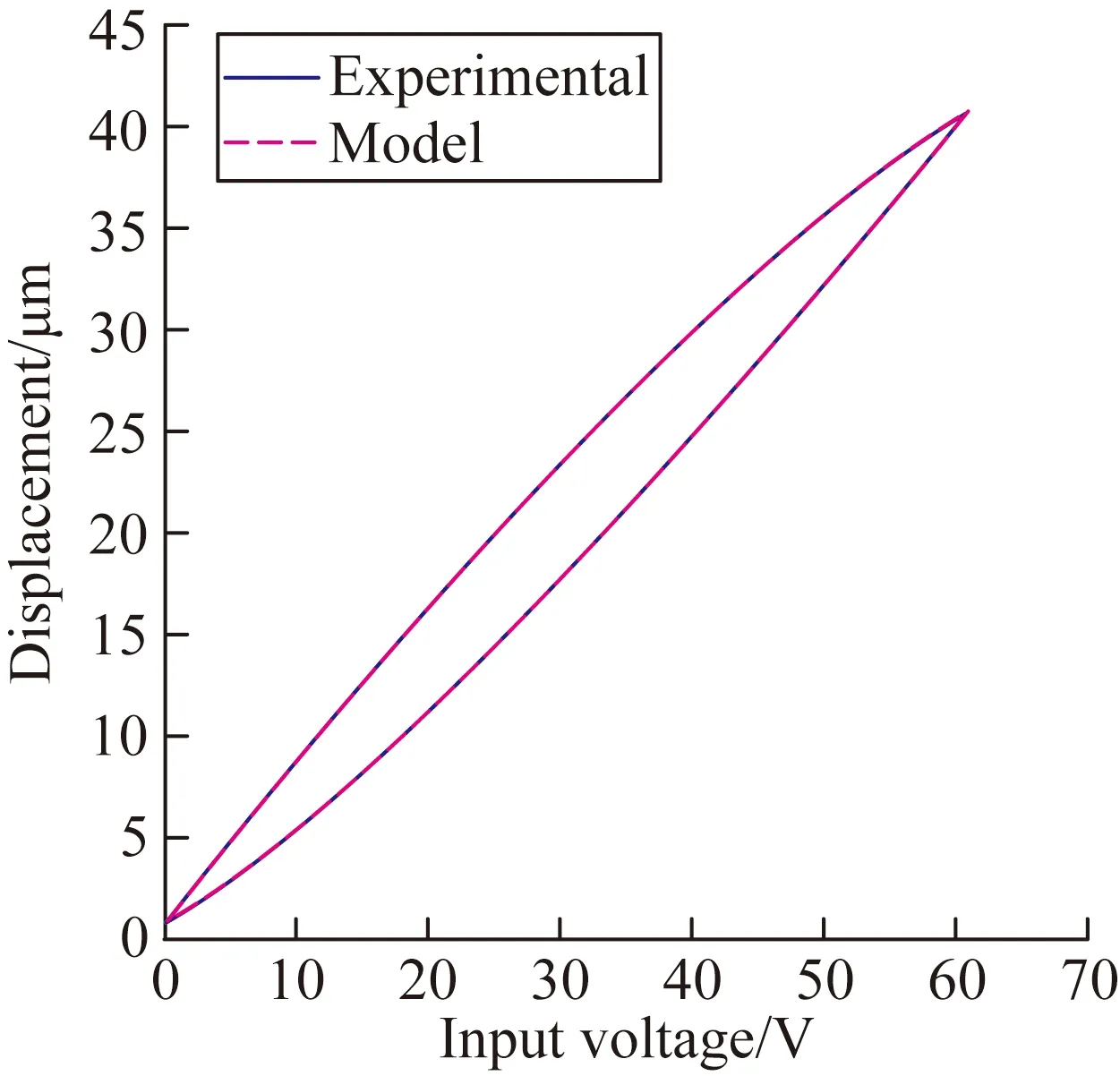
(a)動態模型與實際遲滯環

(b)動態模型的位移誤差與驅動電壓之間的關系曲線

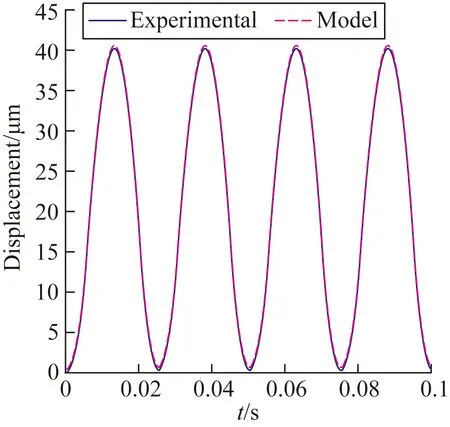
(c)輸出位移時間曲線

圖5模型預測的壓電陶瓷微位移平臺的結果與實驗測量結果的比較

Fig.5Comparisons between predicted results from piezoelectric micro displacement platform by model and measured results

5　結　論

本文提出了一種表征壓電微位移平臺輸出位移與輸入電壓之間關系的動態遲滯模型。主要應用于壓電微位移平臺進行較大行程、快速定位過程中。模型是在Bouc-Wen模型的基礎上加上了壓電微位移平臺的動態特性而建立起來的動態遲滯模型，既能表現出微位移平臺在快速定位過程中出現的動態特性，又能體現出平臺在大行程定位過程中出現的遲滯特性。實驗表明，在最大位移輸出為40 μm，輸入電壓頻率為40 Hz時，模型的最大誤差由單純使用Bouc-Wen模型時的3.04 μm 下降到了0.67 μm。此時，模型的最大相對誤差為1.68%，驗證了該模型能大大提高壓電微位移平臺在快速、大行程定位中的精確度。需要說明的是，實驗驗證以國產代表性的哈爾濱芯明天科技有限公司生產的壓電微位移平臺和驅動器為基礎進行的。在實際應用中，根據壓電微位移平臺類型，僅需在模型的基礎上對其主要參數進行識別，即可得到一種能更加精確描述壓電微位移臺動態遲滯現象的模型，模型具有廣泛適用性。為高性能壓電微位移平臺控制系統的設計提供了參考。

[1]李慶祥，王東生，李玉和.現代精密儀器設計[M]. 北京:清華大學出版社，2004.

LI Q X， WANG D SH， LI Y H.DesignofModernPrecisionInstruments[M]. Beijing:Tsinghua University Press，2004.(in Chinese)

[2]張棟，張承進，魏強.壓電微動工作臺的動態遲滯模型[J]. 光學 精密工程，2009，17(3):549-556.

ZHANG D， ZHANG CH J， WEI Q. Dynamic hysteresis model of piezopositioning stage[J].Opt.PrecisionEng.，2009，17(3):549-556.(in Chinese)

[3]WANG Z W， LI T J. Optimal Piezoelectric sensor/actuator placement of cable net structures using H_2-norm measures [J].Journalofvibration&control， 2014，20(8):1257-1268.

[4]王志斌，李克武，張瑞，等. 基于鈮酸鋰制作光彈調制器用壓電驅動器[J].光學 精密工程，2015，23 (1):63-69.

WANG ZH B， LI K W， ZHANG R，etal.. Fabrication of piezoelectric actuator for photoelastic modulator based on lithium niobate[J].Opt.PrecisionEng.，2015，23(1):63-69. (in Chinese)

[5]劉泊，郭建英，孫永全.壓電陶瓷微位移驅動器建模與控制[J].光學 精密工程，2013，21(6):1503-1509.

LIU B，GUO J Y，SUEN Y Q.Modeling and control for PZT micro-displacement actuator[J].Opt.PrecisionEng. ，2013，21(6):1503-1509. (in Chinese)

[6]LI Z， SU CY， CHAI T. Compensation of hysteresis nonlinearity in magnetostrictive actuators with inverse multiplicative structure for preisach model[J].IEEETransactionsonAutomationScienceandEngineering， 2014，11(11):613-619.

[7]李黎，劉向東，王偉，等.壓電陶瓷執行器遲滯特性的廣義非線性Preisach模型及其數值實現[J].光學 精密工程，2007，15(5):706-712.

LI L， LIU X D， WANG W，etal.. Generalized nonlinear Preisach model for hysteresis nonlinearity of piezoceramic actuator and its numerical implementation [J].Opt.PrecisionEng. ，2007，15(5):706-712. (in Chinese)

[8]GU G Y， ZHU L M， SU C Y，etal.. Modeling and compensation of asymmetric hysteresis nonlineairty for piezoceramic actuators with a modified prandtl-ishlinskii model[J].IEEETransactionsonIndustrialElectronics， 2013，61(3):1583-1595.

[9]方凡，崔玉國，梁冬泰，等.壓電微動平臺的改進PI遲滯模型研究[J].壓電與聲光，2014，36(1):69-75.

FANG F， CUI Y G， LIANG D T，etal..Research on improved hysteresis model of piezoelectric micro positioning stage [J].PiezoelectricandAcoustooptics，2014，36(1):69-75.(in Chinese)

[10]王曉東，江國棟.壓電陶瓷遲滯建模及控制仿真[J].壓電與聲光，2015，37(36):926-929.

WANG X D，JIANG G D.Hysteresis modeling and control simulation of piezoelectric ceramic[J].PiezoelectricandAcoustooptics，2015，37(36):926-929.(in Chinese)

[11]孫孔政.壓電陶瓷系統遲滯非線性建模與控制的研究[D].北京:中國科學院，2013.

SUEN K ZH.Researchbasedonpiezoelectricceramicshysteresisnonlinearmodelingandcontrol[D]. Beijing:Graduate University of the Chinese Academy of Sciences，2013. (in Chinese)

[12]XIAO S L， LI Y M. Dynamic compensation andH∞ control for piezoelectric actuators based on the inverse Bouc-Wen model[J].RoboticsandComputer-IntegratedManufacturing， 2014， 30(1):47-54.

[13]袁剛，張小波，王代華，等. 壓電式快速控制反射鏡的遲滯特性及線性化[J].光學 精密工程，2015，23(6):1650-1656.

YUAN G， ZHANG X B， WANG D H，etal.. Hysteresis and linearization of piezoelectric fast steering mirror[J].Opt.PrecisionEng. ， 2015， 23， (6):1650-1656.(in Chinese)

[14]朱煒，芮筱亭.壓電執行器的Bouc-Wen模型在線參數辨識[J].光學 精密工程，2015，23(1):110-116.

ZHU W， RUI X T. Online parameter identification of Bouc-Wen model for piezoelectricactuator[J].Opt.PrecisionEng. ，2015，23(1):110-116.(in Chinese)

[15]BOUC R．Forced vibration of mechanical systems with hysteresis[C].Proceedingsofthe4thConferenceonNonlinearOscillations，Prague，Czechoslovakia， 1967: 315.

[16]WEN Y K. Method for random vibration of hysteretic systems[J].ASCEJournalofEngineeringMchanics， 1976， 102(2): 249-263.

[17]ADRIAENS H， KONING W， BANNING R.Modeling piezoelectric actuators[J].IEEE/ASMETransactionsonMechatronics， 2000， 5(4):331-341.

楊曉京(1971-)，男，云南大理人，教授，博士生導師，1993年、1996年于中國農業大學分別獲得學士、碩士學位，2008年于浙江大學獲得博士學位，2013年于昆明理工大學博士后出站。主要從事超精密驅動與傳動理論及新技術等方面的研究。E-mail:xjyang@vip.sina.com

彭蕓浩(1991-)，男，廣東樂昌人，碩士研究生，2014年于長春理工大學獲得學士學位，主要從事精密工作臺設計及精密工作臺系統建模、控制方面的研究。E-mail:1713142503@qq.com

(版權所有未經許可不得轉載)

Dynamic hysteresis modeling and experimental verification of piezoelectric positioning stage

YANG Xiao-jing*， PENG Yun-hao， LI Yao

(SchoolofMechanicalandElectricalEngineering，KunmingUniversityofScienceandTechnology，Kunming650500，China)*Correspondingauthor，E-mail：xjyang@vip.sina.com

To improve the precision of rapid positioning of a piezoelectric positioning stage， a positioning model is established to characterize the relationship between driving voltage and output displacement of the platform. As the piezoelectric positioning stage for precision position in the fast and large stroke is not only affected by the hysteresis characteristics of the piezoelectric ceramics， but by the dynamic characteristics， this paper uses Bouc-Wen model to describe the hysteresis characteristics of piezoelectric ceramics， combines with the dynamic characteristics of the piezoelectric positioning stage to establish model， and lets the model reflect the dynamic characteristics and hysteresis characteristics of the platform. To verify the correctness of the model， the experimental equipment based on the piezoelectric micro displacement platform and the related driver is built， and model is verified by experiments， and a secondary development of monitor-control program is performed.The results show that, compared with the previous Bouc-Wen model,when proposed model in the maximum displacement output is 40 μm and the input voltage frequency is 40 Hz,the maximum error is reduced from 3.04 μm to 0.67 μm and the maximum relative error is 1.68%.The results show that the proposed model can better simulate the hysteresis characteristics and dynamic characteristics of the piezoelectric stage, and greatly improve the accuracy of the piezoelectric micro displacement platform in the fast and large stroke positioning.

piezoelectric positioning stage; dynamic characteristics; hysteresis characteristics; Bouc-Wen model; dynamic position

2016-04-10；

2016-05-21.

國家自然科學基金資助項目(No.51365021)

1004-924X(2016)09-2255-07

TP271.4；TH701

A

10.3788/OPE.20162409.2255