基于數據截斷變換的主成分分析回歸預測方法

蘇 嘉，關 毅

（哈爾濱工業大學計算機科學與技術學院，哈爾濱　150001）

基于數據截斷變換的主成分分析回歸預測方法

蘇 嘉，關 毅

（哈爾濱工業大學計算機科學與技術學院，哈爾濱150001）

針對DataCastle學生成績排名預測任務：根據學生以往的在校信息預測下學期的成績排名，結合現有的主成分分析方法以及多元線性回歸模型，本文提出了基于數據截斷變換的主成分分析回歸預測方法，并與其它的方法進行了比較，結果表明：基于數據截斷的主成分分析回歸預測方法能夠更好地預測學生下個學期成績，預測準確率達到78.57%，優于對比的模型，在最終結果排行榜中排在前百分之十，因此可以較好地作為解決其它預測分析問題的工具。

截斷變換；主成分分析；多元線性回歸；預測

0　引 言

大數據分析、挖掘并在此基礎之上的信息預測是當今信息化時代迫切面臨的挑戰和機遇。2014年巴西世界杯無疑是全世界足球愛好者的一場盛宴，而本次世界杯上另一新奇看點就是大數據的分析和預測。谷歌、百度、微軟均各擅勝場地競相給出了自家的賽事評測分析，就是分別根據以往比賽經驗、球員技術、身體狀況等信息成功預測了世界杯的16強。百度和微軟甚至以100%的勝率預測了4強的名單，由此可見大數據的潛在價值。隨著大數據時代的到來，基于事物以往信息的未來狀態預測分析已經愈演愈熱，預測分析在科學研究以及生活中具有廣泛的優勢發展空間，如天氣預測［1］、經濟走勢預測［2］、健康疾病預測等［3-5］。

DataCastle也認識到了大數據的重要性，2014年發布了學生成績排名預測任務：根據學生以往的在校數據，預測接下來一個學期的相對成績排名。隨之也公開了2組數據集：訓練集數據和測試集數據。訓練集數據包括某高校的538名在校大學生3個學期按學號遞增排序的成績排名、按日期遞增排序的圖書借閱記錄、按日期遞增排序的進入圖書館門禁記錄、按地點代碼遞增排序的學生卡消費記錄。測試集數據由另外某學院的91名學生3個學期的這4類信息組成，只不過沒有給出該組學生第三學期的相對成績排名。任務就是要根據訓練集數據訓練預測模型，以在測試集數據上預測測試集里91名學生第三學期的相對成績排名。預測結果需要按91名學生的學號遞增的順序給出，并按照regression-SpearmanR算法計算預測結果和真實排名的Spearman相關性，相關性在［0，1］區間內，越接近于1，表示預測結果和真實排名越接近，具體計算公式如下：

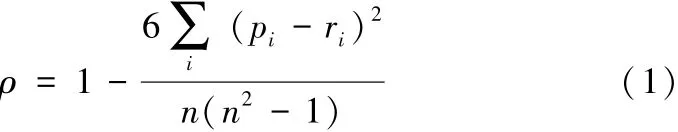
其中，pi，ri分別表示第i個學生預測的相對排名和真實的相對排名，n代表學生數，i=1，2，…，n。這里預測結果的Spearman相關性的計算是由DataCastle根據提交的結果進行的。

該評測的目的在于：一方面，就評測內容本身來說，通過預測結果，使得教育和學習更有目的性和針對性。首先，可以幫助學校制定合理的教學計劃，對可能成績下滑嚴重的同學提出警示，并開展有針對性的教育教學任務；其次，學生通過觀察自己可能出現的成績，自我調整，成績好的可以保持現在的學習生活習慣，成績不理想或有巨大下滑的可以通過改進現有的學習方法和調整生活作息安排來提高成績，避免成績下滑。另一方面，就評測長遠意義來說，通過對數據的處理、預測、以及利用新的方法和技術手段來解決實際問題等過程，為大數據行業注入新的思想和方法以及優秀人才，這將會推動整個大數據行業的發展。

針對該評測，結合現有的主成分分析方法和多元線性回歸模型，本文提出一種新的預測模型算法：基于數據截斷變換的主成分分析回歸預測方法，模型的具體構建過程見第二部分。同時，也對預測結果進行了提交，并就預測結果與其它5組預測方法進行了比較，實驗結果證實了該模型的優異性。

本文第二部分為方法概述，詳細描述了基于數據截斷變換的主成分分析回歸預測方法的理論。第三部分為實驗部分，包括該模型的結果、與其它5組預測方法的比較以及結果分析。第四部分為總結部分。

1　方法概述

針對給出的數據形式，研究考慮對所給信息進行數據統計，并將統計得到的各學期每個學生的借書次數、進入圖書館次數、校園卡消費次數分別來代替圖書借閱信息、進入圖書館門禁信息、學生卡消費信息。該方法的結構流程如圖1所示。

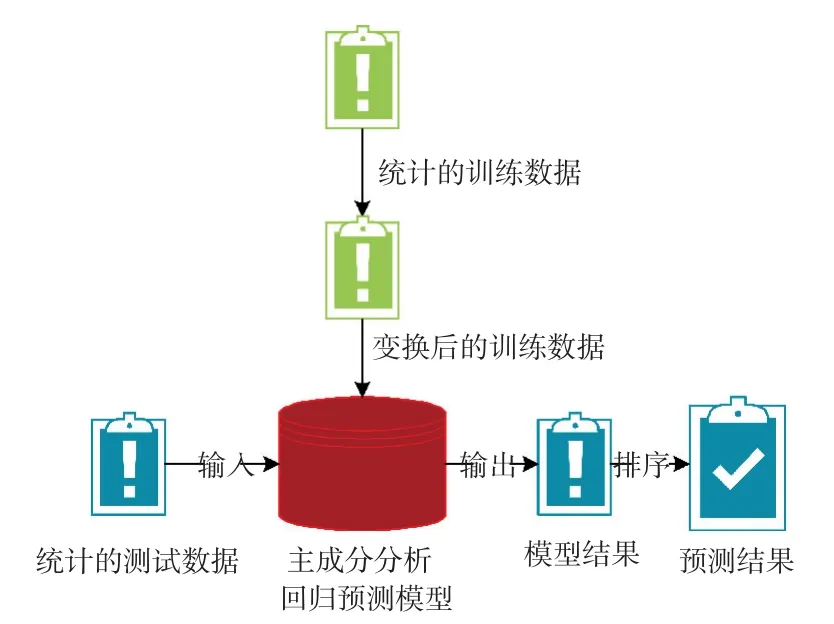
圖1　方法結構圖Fig.1 Structure of the model

由圖1可知，將統計的訓練集數據進行數據截斷變換。之后，用得到的變換后訓練數據對主成分分析回歸預測方法進行訓練，直至模型訓練完畢。接著，對統計得到的測試集數據進行數據截斷變換，并將變換后的測試數據輸入已訓練好的主成分分析回歸預測方法，得到模型輸出結果，再對結果進行相關排序，從而得到最終預測結果。下面詳細介紹該方法的實現過程。

對于統計得到的各個變量數據：3個學期的借書量B1、B2、B3，進入圖書館的次數E1、E2、E3，校園卡消費次數C1、C2、C3，其中數值很小或者很大的點只有極少數。此處需要對每個變量的這些異常數據進行處理以使得這些極少的數據不會在較大程度上影響回歸模型，從而提高預測結果的準確性。研究中利用上、下截斷點作為判斷數據異常的準則。要理解上、下截斷點，首先得給出上、下四分位數Q3、Q1的概念。所謂上、下四分位數即為在一組從小到大的已經完成排序的數據中處在3/4位置和1/4位置的數據。在此概念基礎上，上截斷點T1就可以由以下公式得出：

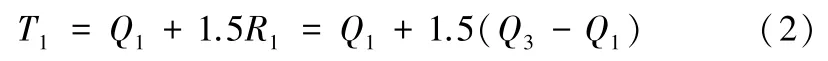
而下截斷點T0則可以由以下公式得出：

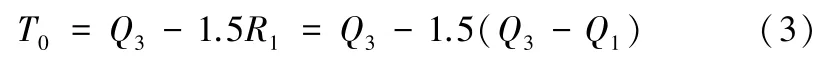
其中，R1=Q3-Q1表示的是四分位極差［6］。

計算得到了上、下截斷點后，將對統計數據x（x∈B1，B2，…，C3）進行如下數據截斷變換：

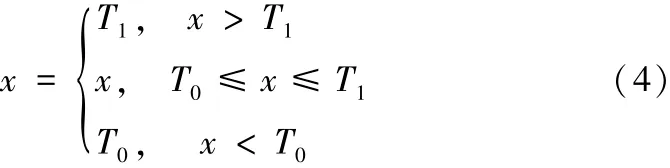
這里的T0、T1即為對應的x所取變量的下截斷點和上截斷點。

從所給變量來看，能影響第三學期成績的預測因素有：前兩學期的學生成績S1、S2，3個學期的借書量B1、B2、B3，進入圖書館的次數E1、E2、E3，校園卡消費次數C1、C2、C3。考慮到影響因素眾多，而研究中卻希望能用較少的變量來盡可能詳實地構建表達第三學期的成績排名。降維的思想即已成為關鍵，這里采用的是主成分分析法［7-9］。主成分分析是多元統計學科中分析數據的一個重要方法，能夠有效地減少影響因變量的因素，起到降低自變量維數的作用。同時，研究發現這些自變量中還有一些信息的重疊，如第一學期和第二學期的成績排名，第一學期借書量和第二學期借書量等，用如上量值表達對第三學期成績的影響時，重疊信息即會成為冗余性工作，只會增加計算量并可能會對結果形成負面的影響。而主成分分析則能夠將自變量中有重疊部分的信息合并在一起，再通過線性變換將原來相關的變量轉化為不相關的變量，合成后的新變量兩兩之間則彼此互不相關，并且新變量還能盡量地保留原來自變量的指示信息。變換的具體形式可如下所示：

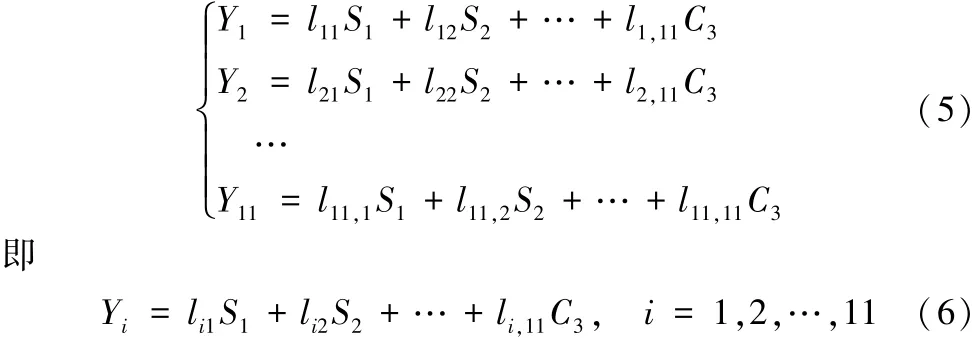
用原來11個變量的線性組合形成的新變量來代替舊變量，并且新變量要盡可能多地涵蓋所有舊變量的信息，也就是新變量的方差越大、整體實現效果越佳。選取方差最大的新變量Yk1（k1∈｛1，2，…，11｝）為第一主成分，如果第一主成分所涵蓋的信息不足以代表原來的11個變量信息，則在剩下的新變量中再選取方差最大的Yk2（k2∈｛1，2，…，11｝/｛k1｝），作為第二主成分，以此類推，直到選取的所有主成分信息足夠涵蓋原來舊的變量信息（在90%以上即可）。同時為了避免有如舊變量一樣的信息重復，主成分之間必須是線性無關的，故在做變量的線性組合（5）時，選擇的系數就必須滿足一定條件以使新變量兩兩之間均能呈現為線性無關。下述引理即已給出了主成分選擇的方法。

引理1［6］當總體X=（X1，X2，…，Xp）T的協方差矩陣∑=（aij）p已知時，設協方差矩陣∑的特征值是λ1≥λ2≥…≥λp≥0，對應的單位正交特征向量為e1，e2，…，ep，則X的第k個主成分為：

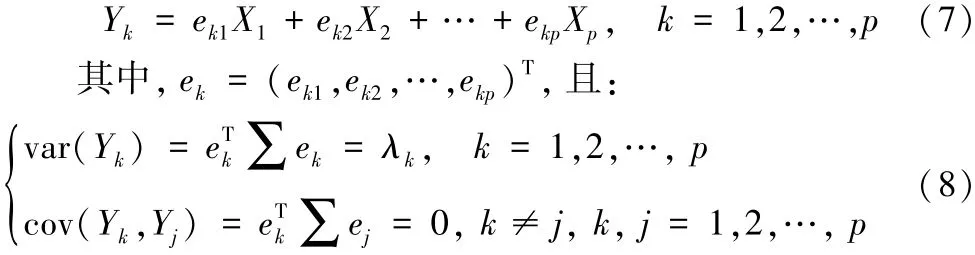
結合以上引理，通過求解原來11個影響變量的協方差矩陣、協方差矩陣的特征值以及單位正交特征向量，就可以得到滿足條件的主成分。此時再根據對應的主成分所包含的原來變量的信息，選取所需要的主成分。在主成分選取完成后，就可基于主成分變量進行多元線性回歸模型的訓練。回歸模型訓練結束后，對測試集數據實施預測［10-12］。

2　實驗設計與結果分析

在這一部分，研究擬定將該模型與其它5組預測模型進行比較，并對該模型的優劣性質及表現展開分析。

2.1基于數據截斷變換的主成分分析回歸預測方法

該實驗采用未變換的統計數據與經過數據截斷變換（4）的數據進行主成分分析回歸預測分析，并將結果進行比對以判定模型優劣。其中以3個學期的借書量為例，分布結果如圖2所示。

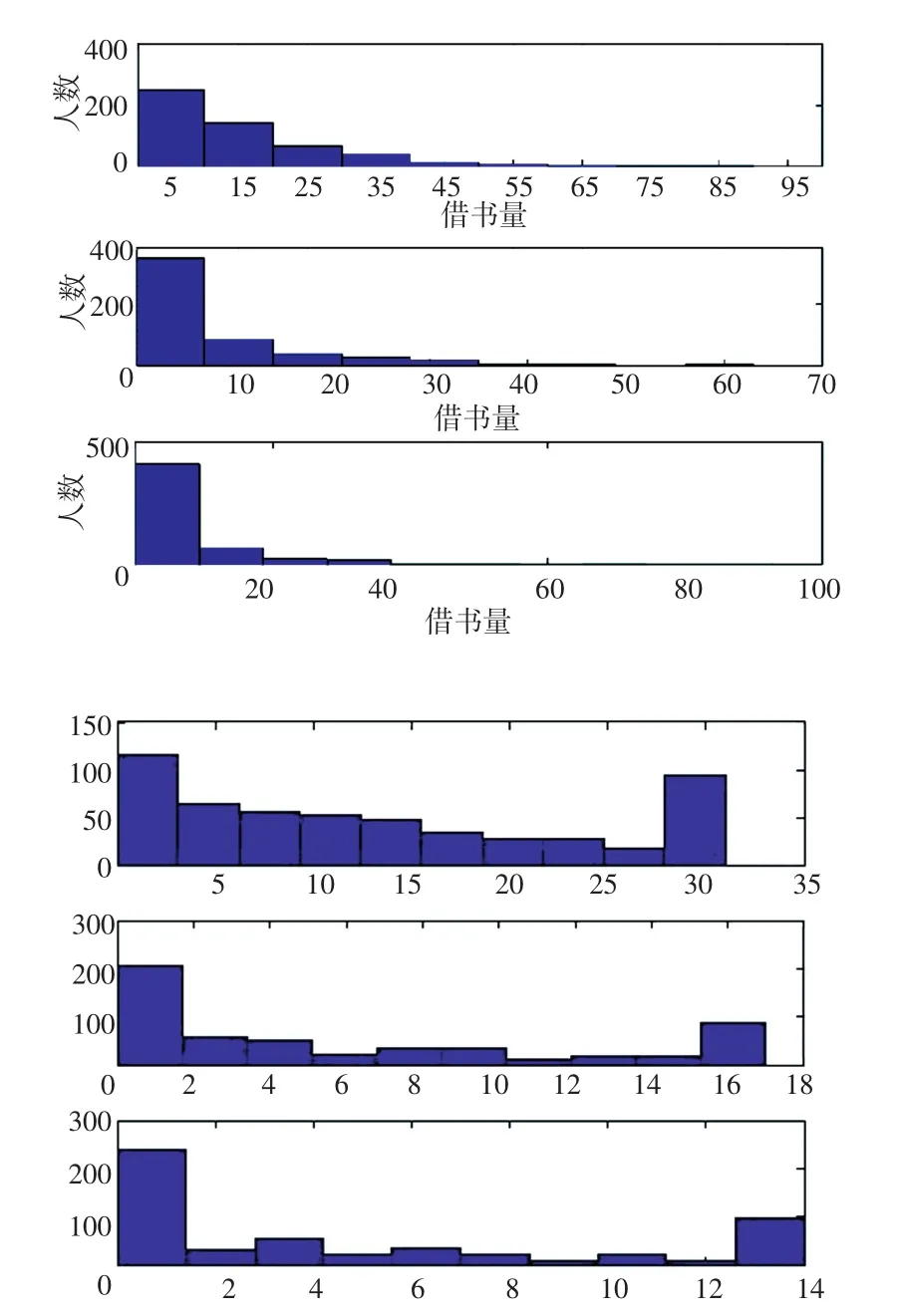
圖2　未變換數據與變換后數據Fig.2 Untransformed data and transformed data

圖2中上面3幅為3個學期的借書量與人數的分布圖，而下方3幅為經過數據截斷變換之后的借書量與人數的分布圖。從圖中可以看到經過數據變化之后兩端的數據都變少了（大于上截斷點的數據以及小于下截斷點的數據均被縮小和放大了）。同時，研究中也對其余的幾個統計變量進行同樣的變換處理。利用處理過的數據（訓練集和測試集）進行主成分分析回歸預測方法的訓練以及預測，得到結果如表1所示。

通過提交2組結果，對比預測準確率可以看出，經過數據截斷變換的主成分分析回歸預測方法比基于未變換數據的主成分分析回歸預測方法的預測準確率要更顯優越，由此證明了數據截斷變換的有效性。

表1　主成分分析回歸預測方法準確率對比Tab.1 Spearman accuracy of PCA

2.2不同預測方法的比較

為了驗證本方法的有效性，本節將考慮其他參賽者使用的數據變換—拉依達變換，和預測模型—BP神經網絡預測模型。

所謂拉依達法又稱拉依達準則、3σ準則，是指對于一個變量x的一組樣本數據x1，x2，…，xn，記其平均值為，標準差為σ，則對于這組數據中的點xi，如果滿足：

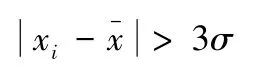
即可判定點xi是誤差粗大值的壞點，應將其剔除［13］。對于統計變量B1，B2，…，C3，可以采用拉依達法進行誤差粗大值的剔除，去除數據中不好的那些點。同時在選取樣本時，實際選取了所有這些學生，學生的各種統計變量的值都沒有被剔除，也就是其各項指標都不是誤差粗大值的壞點，研究中就將用拉依達法剔除壞點，并選取剔除之后的樣本的過程叫做拉依達變換。

BP神經網絡是一種誤差反向傳播的神經網絡［14］，通過梯度下降法使傳遞誤差達到最小值，進而反向調整神經網絡中鏈接的權值，使得模型得到的實際結果和真實結果誤差達到最小。該模型是一種有監督的學習模型，具有現實鮮明的自組織和自適應能力，在很多領域中都有廣泛的應用［15-17］。對于最簡單的隱含層只有一層的BP神經網絡，具體的網絡拓撲結構可如圖3所示。

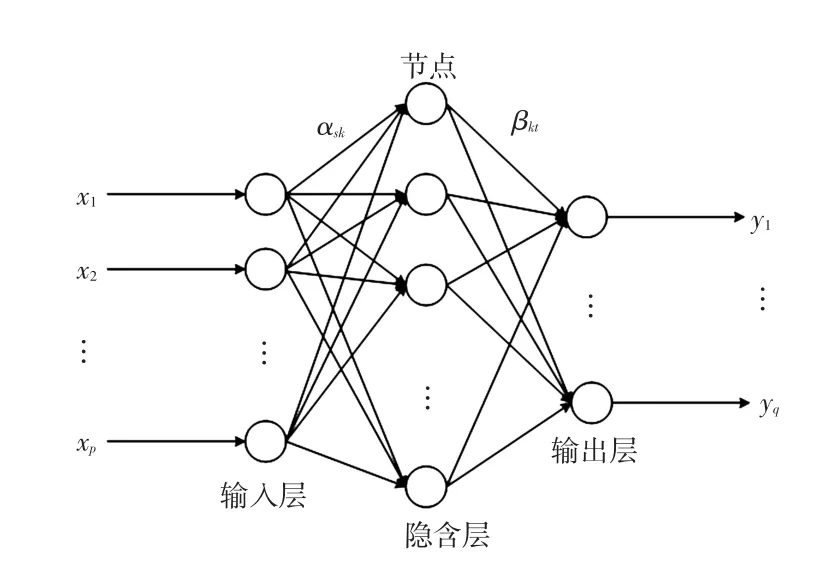
圖3　BP-神經網絡拓撲圖Fig.3 Topological graph of BP-neural network

對于經過拉依達變換的數據，對應的BP神經網絡預測模型訓練則如圖4及圖5所示。

圖4為用經過拉依達變換的數據進行神經網絡預測模型的效果預測時，誤差和訓練時間的關系圖，可以看出誤差逐漸趨向于一個恒定的值，在一定時間之后基本保持誤差在極小值的一個最佳區間范圍內，此時已達到訓練的目的。圖5為用經過拉依達變換的數據進行網絡訓練之后的擬合程度，從中能夠看到網絡輸出值和真實值的擬合度已高達0.957 47。此時，網絡中的各個參數已訓練完畢。

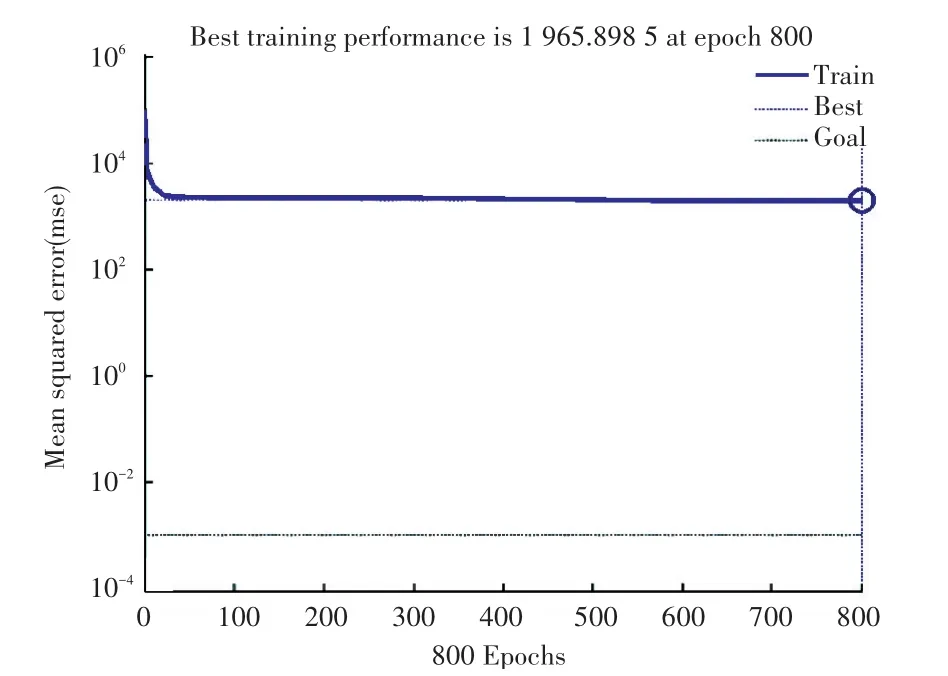
圖4　基于數據拉依達變換的神經網絡訓練過程Fig.4 Training process of BP-neural network based on Pau Ta transformation

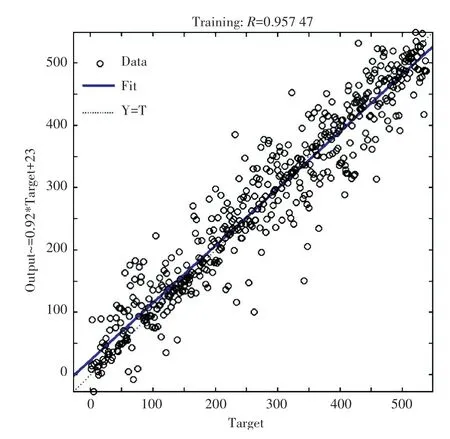
圖5　基于數據拉依達變換的神經網絡訓練擬合結果Fig.5 Fitting result of the BP-neural network based on Pau Ta transformation

此后，還進行了一系列組合對比試驗，可得實驗結果如表2所示。

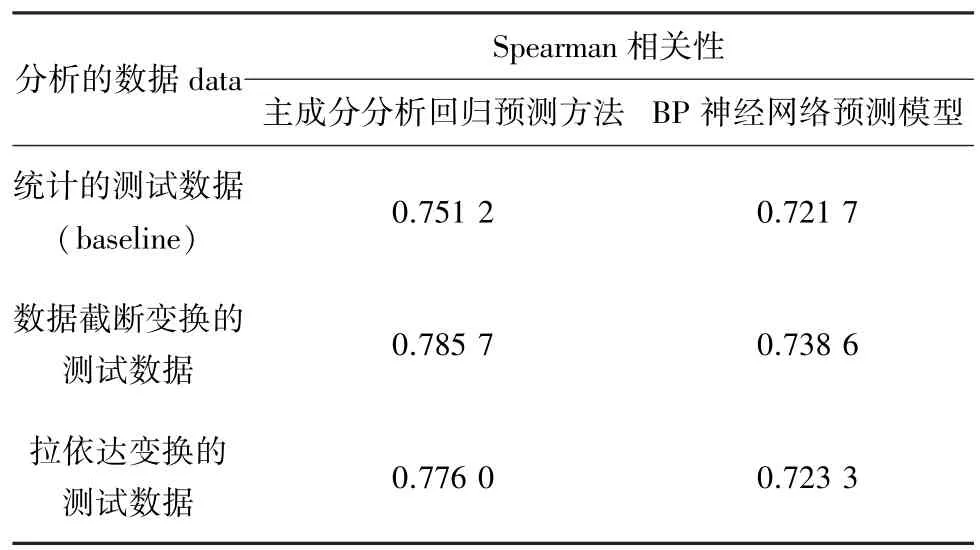
表2　各預測模型預測準確度Tab.2 Spearman accuracy of models

通過分析表2可以得出，基于數據截斷變換的主成分分析回歸預測方法具有最高的預測準確度。無論是基于哪類數據，主成分分析回歸預測方法的結果比BP神經網絡預測模型預測結果都要表現出更高的準確度；而基于數據截斷變換的測試數據預測結果在準確度上則要明顯超出基于統計的測試數據以及基于拉依達變換的測試數據的實驗效果。

2.3結果分析

在第二部分方法概述里所介紹了主成分分析回歸預測方法的構建，這也可以映射得出其具備的特點，將有關聯的變量轉化為獨立的變量，在做回歸分析的時候就能夠訓練出更精確的回歸模型，最終結果中也證明了主成分分析的優異性。

對于BP神經網絡的不佳表現，則是因BP神經網絡的特性所致。對于訓練集數據，擬合程度可以很高，這既是優點，也已成為缺點。過度擬合的模型對測試集的數據進行預測，將不會得到理想中的預測準確度。為了得到更好的準確度，就需要不斷地調試與訓練集相關聯的目標模型，從而使得對于測試集預測結果能達到最優，這將會是一項費時費力的工作。

另外，分析基于拉依達變換的預測準確度要比基于數據截斷變換的預測準確度略低這一結果事實可知，則是由于在涉及拉依達變換進行樣本的剔除過程中，一些“重要”的數據點信息被刪除了，而利用這些殘缺的數據信息訓練出來的模型將無法完整表達變量內部之間的聯系，用測試集數據做預測時預測準確度就不會高。而經過數據截斷變換的數據則因沒有剔除掉這些異常樣本，而只是在原有的數據基礎上進行了一定的壓縮，相比較拉依達變換而言，過程中保留了所有的原始樣本，因而信息繼承較為完好。

3　結束語

本文針對的問題是：預測學生未來成績排名，結合現有的一些方法和手段提出了基于數據截斷變換的主成分分析回歸預測方法，并在實驗部分對預測準確度進行了討論，對比了其它5組預測方法，實驗結果證明基于數據截斷變換的主成分分析回歸預測方法比其它5組方法的預測準確度要高。得到的模型可以對其它相關問題進行預測分析，同時下一步的工作即是需對數據處理和預測模型做進一步的改進，以提高預測準確率。

［1］鳳英.現代氣候統計診斷與預測技術［M］.北京：氣象出版社，1999.

［2］吳世農，盧賢義.我國上市公司財務困境的預測模型研究［J］.經濟研究，2001，6（2008）：4.

［3］李連弟，魯鳳珠，張思維，等.中國惡性腫瘤死亡率20年變化趨勢和近期預測分析［J］.中華腫瘤雜志，1997，19（1）：3-9.

［4］孫秀娣，牧人，周有尚，等.中國胃癌死亡率20年變化情況分析及其發展趨勢預測［J］.中華腫瘤雜志，2004，26（1）：4-9.

［5］楊玲，李連弟，陳育德.中國2000年及2005年惡性腫瘤發病死亡的估計與預測［J］.中國衛生統計，2005，22（4）：218-221.

［6］李柏年，吳禮斌.MATLAB數據分析方法［M］.北京：機械工業出版社，2012.

［7］JOLLIFFE I.Principal component analysis［M］.New York：John Wiley&Sons，Ltd，2002.

［8］WOLD S，ESBENSEN K，GELADI P.Principal component analysis［J］. Chemometrics and intelligent laboratory systems，1987，2（1）：37-52.［9］ABDI H，WILLIAMS L J.Principal component analysis［J］.Wiley Interdisciplinary Reviews：Computational Statistics，2010，2（4）：433-459.

［10］AIKEN L S，WEST S G，PITTS S C.Multiple linear regression［J］. Handbook of Psychology，2003，4（19）：481-507.

［11］KUTNER M H，NACHTSHEIM C，NETER J.Applied linear regression models［M］.New York：McGraw-Hill/Irwin，2004.

［12］ANDREWS D F.A robust method for multiple linear regression［J］. Technometrics，1974，16（4）：523-531.

［13］ZHANG L，QIN Y，ZHANG J.Study of polynomial curve fitting algorithm for outlier elimination［C］//Computer Science and Service System（CSSS）2011，International Conference on.Nanjing：IEEE，2011：760-762.

［14］MCCLELLAND J L，RUMEHART D E.Parallel Distributed Processing（Two Volumes）［M］.Cambridge，Massachusetts：MIT press，1986.

［15］PATTERSONDW.Artificialneuralnetworks：theoryand applications［M］.New Jersey：Prentice Hall PTR，1998.

［16］劉洪蘭，張強，張俊國，等.BP神經網絡模型在伏旱預測中的應用——以河西走廊為例［J］.中國沙漠，2015（35）：474-478.

［17］ZHANG G，PATUWO B E，HU M Y.Forecasting with artificial neural networks：The state of the art［J］.International journal of forecasting，1998，14（1）：35-62.

A new regression model of principal component analysis based on the data with truncated transformation

SU Jia，GUAN Yi
（School of Computer Science and Technology，Harbin Institute of Technology，Harbin 150001，China）

Combine with principal component analysis and multiple linear regression methods，a new regression model based on the data with truncated transformation is proposed in the prediction of students’future performance at school，one of the tracks of 2014 DataCastle.Experiments show that compared with other predict methods，the proposed model perform in an efficient way.The accuracy of the proposed model reaches highly as 78.57%，better than any others methods，and ranks in the top ten percent of the ranklist.This model not only has the availability in this area，but also can be used in other prediction researches.

truncated transformation；principal component analysis；multiple linear regression；predict

TP391

A

2095-2163（2016）03-0001-05

2015-12-13

蘇 嘉（1991-），男，博士研究生，主要研究方向：醫療健康信息學、自然語言處理、機器學習；關 毅（1970-），男，博士，教授，博士生導師，主要研究方向：自然語言處理、醫療健康信息學、認知語言學等。