論自復位防屈曲支撐鋼框架減震性能

張 國 鋒

(賽鼎工程有限公司，山西 太原　030032)

?

論自復位防屈曲支撐鋼框架減震性能

張 國 鋒

(賽鼎工程有限公司，山西 太原030032)

介紹了自復位防屈曲支撐的構造原理，采用ANSYS有限元軟件，建立了自復位防屈曲支撐滯回模型，數值分析了自復位防屈曲支撐鋼框架的減振性能，得出了一些有價值的結論。

防屈曲支撐，鋼框架，復位系統，地震響應

防屈曲支撐發展至今已經有大約40年的歷史，技術趨于成熟、制度標準相對比較完善，是一種有效的對抗側力的減震設備。在強震或者中震中，防屈曲支撐能夠實現全截面的屈服，不會對局部或者整體結構產生損壞，有效的對地震所產生的能量進行耗散。然而，防屈曲支撐鋼框架結構可以依靠其所具有的形變能來消耗強大外力帶來的能量。防屈曲支撐結構在強震的作用下，肯定會發生較大的殘余變形。自復位防屈曲支撐鋼框架在殘余變形方面具有較好的復位能力，有效的解決了殘余變形的問題。

1　自復位防屈曲支撐的構造原理

1.1自復位防屈曲支撐的基本構造

自復位防屈曲支撐鋼框架結構由內方鋼管和外方鋼管兩者組成起到支撐的作用。在內管和外管的上部需要安裝一個連接板，對各個構件來進行連接(見圖1)。左側的連接管由槽孔和內管兩者進行連接來對其進行固定；右側的連接管由槽孔和內管兩者進行連接來對其進行固定。外管的中間位置設置有槽孔，穿過槽孔將內部和外管的摩擦板進行連接，借助高強螺栓進行固定。左右端板上有四根高強度的鋼絞線固定于此，并且借助端板將預應力來進行傳遞，從而形成一個完整的支撐結構。

1.2自復位防屈曲支撐的工作原理

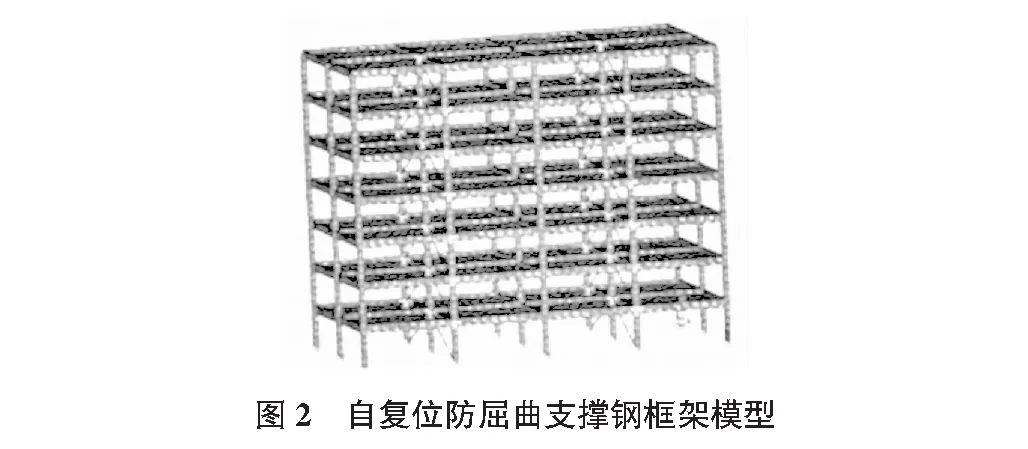
在自復位防屈曲支撐鋼框架的兩側同時給一個外力，當外荷載力與內管、外管的摩擦力之和小于鋼絞線的預應力時，即0PO+F時，則自復位防屈曲支撐鋼框架的內管和外管會發生一定程度的位移，并且產生一定的能耗；當外荷載P開始減小時，當PO-F≤P≤PO+F時(PO≈1.2F)，摩擦板之后會形成方向作用力，不發生耗能；當P

2　ANSYS計算模型的建立

2.1自復位防屈曲支撐滯回模型的建立

支撐滯回模型的建立借助計算機完成，采用七層五榀兩跨的結構。自復位防屈曲支撐鋼框架模型的建立需要從底部連續向上進行建立，連續布置于第二榀及第四榀框架結構中，如圖2所示。框架層高大約為3.6 m，跨距為7.7 m，處于第Ⅲ類場地，地震分組第二組，抗震設防烈度為8度，強震結構中阻尼比為0.55。在軟件中沒有符合自復位防屈曲支撐模型的滯回模型，所以，需要將滯回模型分為兩個模型來進行分析，并且兩者都可以使用軟件來對其進行分析，將兩者模型所得到的結構進行疊加就得到自復位防屈曲支撐的模型。

2.2材料特性及相關參數

自復位防屈曲支撐鋼框架將雙線性隨動硬化材料模型來作為梁和柱的材料，并且材料的彈性數值為2.06×105MPa，材料的屈服強度為205 MPa，材料的泊松比為0.3，材料的密度為7 850 kg/m3，材料的強化模量為4 120 MPa。

自復位防屈曲支撐鋼框架采用相同的兩個Link8單元來進行模型的搭建，最為關鍵的模型材料為多彈性材料，彈性的模量數值為1.3×106MPa，泊松比為0.3，應變點和應力點分別為0.000 3和390 MPa，0.01和1 950 MPa；另一個為雙線性隨動硬化材料模型，彈性的模量數值為1.2×106MPa，泊松比為0.3，屈服強度為360 MPa，強化模量為0，密度為7 850 kg/m3。相同的Link8單元截面實常數值為0.001 m2，其長度為8.32 m。

防屈曲支撐采用單一的Link8單元來進行模型的搭建，采用的材料模型是雙線性隨動硬化材料模型，其中，彈性的模量數值為2.06×105MPa，泊松比為0.3，屈服強度為345 MPa，強化模量為6 589 MPa，密度為7 850 kg/m3。Link8單元截面實常數為0.002 2 m2，長度為8.32 m。

各項相同的彈性材料模式為樓板，其彈性模量為3.0×104MPa，泊松比0.3，樓板的厚度為0.15 m，密度為2 500 kg/m3。

2.3邊界條件及地震波的施加

自復位防屈曲支撐鋼架的柱腳節點需要與地基進行焊接，并且梁和柱的結點也需要借助焊接的方式來進行固定，支撐板與梁、柱的結點需要借助耦合的方式來進行連接和固定。樓板的荷載值大約為2 kN/m2，所具有的重力加速度為9.81 m/s2，積分步長0.01 s，可持續的時間大約為19.19 s。為了更好的模擬強震環境中的地震效果，將地震波的數值需要調節到400 cm/s2，如圖3所示。為了更加準確的得到在強震環境下自復位防屈曲支撐鋼架的殘余變形數值，因此，需要增加20 s的加速度。

3　結果對比

3.1對比準則的建立

自復位防屈曲支撐鋼架和防屈曲支撐鋼框架兩者在支撐方面具有共同點。因此，在進行實驗時，需要選擇759 kN的屈服力來進行對比。地震響應需要與第三榀框架梁保持平行狀態，借助柱結點UX方向的位移數值來對自復位防屈曲支撐鋼架和防屈曲支撐鋼框架的復位情況進行比較。

3.2結構地震響應分析

為了有效的對自復位防屈曲支撐結構的抗震性能進行充分的考察，需要對自復位防屈曲支撐(SCBRB)鋼框架和防屈曲支撐(BRB)鋼框架、無支撐抗彎鋼框架(NMRF)三者進行時程分析研究。抗彎鋼框架結構中主體框架不但需要承擔重力，而且還需要梁柱構件的彎曲變形來對外力進行抵抗。

自復位防屈曲支撐鋼框架中，αs為0.5，αc為0.5，β為0.5，αB/M取3.0，依照數據來進行結構的設計。為了更好的對自復位防屈曲支撐鋼框架和防屈曲支撐鋼框架具有對比性，在進行設計時，需要將自復位防屈曲支撐和防屈曲支撐的第一軸向剛度和軸向屈服力相同。自復位防屈曲支撐和防屈曲支撐軸向參數見表1，各層結構的支撐截面相同，初始周期相同。

表1　SCBRB及BRB支撐參數

時程分析結構如表2所示。表2中所顯示的數據為第三條地震波的包絡值。通過數據可以看出，在強震的作用下，普通的抗彎鋼框架最大的位移角達到了7.2%，殘余變形也達到了5.6%;防屈曲支撐鋼框架中最大位移角為2.8%，殘余變形位移角為0.8%；自復位防屈曲支撐鋼框架中由于存在復位系統，其殘余變形位移角小于0.1%。但是，自復位防屈曲支撐鋼框架和防屈曲支撐鋼框架的剪重比相差不多，主要是由于自復位防屈曲支撐鋼框架的第二剛度力大于防屈曲支撐鋼框架。所以，將位移角作為評價的指標更加的科學合理。

表2　不同結構的響應

4　減震效果的影響參數分析

4.1支撐與主體結構剛度比αB/M

支撐結構和主體結構之間的剛度比αB/M越大，支撐結構所發揮的作用就越大。建筑物的高度一定時，結構的合理基本周期值相對穩定。支撐結構和主體結構的剛度比αB/M越大，主體結構發揮的剛度力越小。因此，可以對梁柱結點的連接方式進行改變，來對主體結構的剛度進行改變。

選擇為αB/M為3，5，7的3個結構，可以得到主體框架的周期和整體結構周期之比以及其剛度之間的關系:

(1)

結構的周期TMO，TTO與剛度比αB/M之間的關系：

(2)

當αB/M=3時，支撐結構中最大的位移角和層間的位移角數值最小，是αB/M為5，7的0.8倍，主要原因是當αB/M=3時，結構中的總剛度為最大值，αB/M=3時，底部的剪力為最小值，由此可以看出結構處于非線性工作的環節。可以從控制殘余變形和最大變形的角度來進行分析，在地震作用力下，當梁端αB/M=3時，是最科學的選擇。

4.2耗能系統與復位系統的屈服力比β

耗能系統和復位系統之間的屈服力比用β表示，β可以對復位防屈曲支持結構的耗能能力產生影響，β值越大，則系統耗能的能力就越強。當β=0時，代表耗能曲線飽滿；當β=0.9時，代表無耗能，兩種結構的模型如圖4所示。主體結構梁柱結點采用剛接模式，在進行設計時，結構和參數保持不變，僅對β數值進行改變。為了使結構更加的具有可比性，需要選擇不同的β數值，并且使β=0和β=0.9的結構模型中初始剛度和第二剛度保持相同，具有相同的屈服力。

當β=0時自復位防屈曲支撐框架結構模型的層間位移角為4.8%，當β=0.9時，自復位防屈曲支撐框架結構的層間位移角為4.0%，由此可以看出，主體結構已經明顯屈服，支撐復位可以從殘余變形的位置恢復到初始位置。當β=0時，結構的位移角較大，由此說明耗能系統可以對自復位防屈曲支撐結構具有一定的減震作用。為了使得結構中耗能和復位達到平衡，需要將β控制在0.5～0.9之間。

4.3耗能系統與復位系統的剛度比αc

在確保β值不發生變化時，αc的大小與系統的屈服有關，并且αc會對滯回曲線的飽滿程度產生影響，也就是對結構的耗能能力產生影響。當αc為0.1,0.3,0.5時，三個不同結構模型中初始周期相同。對結構進行分析之后，當αc為0.1,0.3時，結構模型中最大層間位移角和殘余層間位移角相差較小，當αc為0.5時，結構模型中最大層間位移角和殘余層間位移角數值最小。由此可見，最大位移的大小會隨著αc的增大而減小。

5　結語

通過對三種不同模型的最大層間位移角、殘余層間位移角等進行對比，發現自復位防屈曲支撐結構具有明顯的優勢。自復位防屈曲支撐鋼框架在殘余變形方面具有較好的復位能力，減少了鋼框架結構的殘余變形。

[1]劉璐,吳斌,李偉.一種新型自復位防屈曲支撐的擬靜力試驗[J].東南大學學報(自然科學版),2012(3)：72-73.

[2]潘振華,潘鵬,葉列平.自復位鋼框架節點有限元模擬及參數分析[J].建筑結構學報,2011(3)：57-59.

[3]郭彥林,王小安,江磊鑫.裝配式防屈曲支撐構件及框架設計理論[J].結構工程師,2010(6)：101-102.

Onvibrationattenuationperformanceofself-centeringbuckling-restrainedbrace

ZhangGuofeng

(Saiding Engineering Co., Ltd, Taiyuan 030032, China)

Thepaperintroducesthecomponentprinciplefortheself-centeringbuckling-restrainedbrace,adoptstheANSYSfiniteelementsoftware,establishesthehystereticmodeloftheself-centeringbuckling-restrainedbrace,undertakesthenumericanalysisofitsvibrationattenuationperformance,andpointsoutsomevaluableconclusion.

buckling-restrainedbrace,steelframework,resetsystem,seismicresponse

1009-6825(2016)23-0038-03

2016-06-03

張國鋒(1975- )，男，高級工程師

TU352

A