基于平衡系數的Active Demons 非剛性配準算法

薛鵬　楊佩　曹祝樓　賈大宇　董恩清

基于平衡系數的Active Demons 非剛性配準算法

薛鵬1楊佩1曹祝樓1賈大宇1董恩清1

經典的Active demons算法利用參考圖像和浮動圖像的梯度信息作為驅動力，并使用均化系數調節兩種驅動力之間的強度.該算法克服了Demons算法單一使用參考圖像的梯度信息作為驅動力的缺點，但是Active demons算法中的均化系數無法同時兼顧大形變和小形變區域的準確配準，還會導致配準的收斂速度和精確度相互制約的問題.為此，本文提出一種新的Active demons非剛性配準算法.提出的算法在Active demons擴散方程中引入一個稱為平衡系數的新參數，與均化系數聯合調整驅動力，不僅可以兼顧圖像中同時具有的大形變和小形變區域的準確配準，而且在一定程度上緩和了收斂速度和精確度相互制約的問題.為了進一步提高配準的收斂速度和精確度，避免陷入局部極值，在新的配準算法的實現中引入由粗到細的多分辨率策略.在Checkboard測試圖像、自然圖像和醫學圖像上的實驗結果表明，提出的算法較經典的Active demons算法收斂速度更快，配準精度平均提高了54.28%，接近最新的TV-L1光流場圖像配準算法的配準精度，解決了Active demons算法存在的問題.

非剛性配準，Active demons算法，光流場圖像配準，驅動力，多分辨率策略

引用格式薛鵬，楊佩，曹祝樓，賈大宇，董恩清.基于平衡系數的Active demons非剛性配準算法.自動化學報，2016，42（9）：1389-1400

圖像配準是圖像處理和計算機視覺等領域的熱點研究問題，廣泛應用于遙感圖像拼接、目標定位和疾病診斷治療等方面.一般我們將配準過程中固定不變的圖像稱為參考圖像，將施加變換的圖像稱為浮動圖像.圖像配準通過進行參考圖像和浮動圖像的空間變換，最終使得參考圖像和浮動圖像對齊.一般來說，圖像配準在不同領域存在一定差異，比如：將多幅遙感圖像拼接成一幅更大的圖像，多幅圖像之間有重疊部分，重疊部分的特征提取是配準的關鍵；而在醫學圖像配準中，兩幅圖像之間幾乎是完全重疊的，研究關注的核心問題是圖像的非均勻形變.按照配準過程中圖像是否存在形變來劃分，圖像配準分為剛性配準和非剛性配準.其中，非剛性圖像配準是近年來的研究熱點之一［1］.非剛性配準算法可以分為基于特征和基于灰度的兩類算法.雖然基于特征的配準算法運算速度較快，但是特征提取和特征匹配往往又是一個困難的問題，對那些特征不清晰的圖像，該類算法存在一定的局限性.而基于灰度的配準算法直接利用圖像灰度的梯度信息，避免了特征提取過程中可能涉及的人工干涉，完全自動處理，受到越來越多的青睞.

基于光流場理論［2］的Demons算法最初由Thirion［3］提出，是一種基于灰度的全自動配準算法.該算法將配準視作擴散問題，在圖像之間的形變較小的前提下，可利用參考圖像灰度的梯度和兩幅圖像的差值來估計浮動圖像的形變.Demons算法具有完備的數學理論基礎和高效的配準性能，廣泛應用于各種圖像配準中，特別是醫學圖像的配準［3-10］.Hellier等［11］對常用的6種配準算法對比研究表明，Demons算法配準精度高于其他5種配準算法.然而，Demons算法存在以下不足：1）僅采用參考圖像的梯度信息驅動形變，收斂速度慢；2）在參考圖像梯度信息接近于零時，浮動圖像的形變方向不能確定，將導致錯誤的配準變換；3）Demons算法建立在圖像之間存在小形變的假設之上，對于形變較大的圖像，Demons算法基于圖像灰度很難準確估計形變.

針對以上的問題，Rogelj等［12］和Wang等［13］提出Active demons算法，將浮動圖像的梯度信息也引入擴散方程，將來自兩幅圖像的兩個單向力疊加為一個合力，引入均化系數α調節驅動力的強度.該算法很好地克服了Demons算法無法配準形變相對較大的圖像的缺陷，且大幅提高了配準速度和精確度.但是，Active demons算法僅通過均化系數α調節驅動力的強度，也存在很大的缺陷：當α取值較大時，驅動力較小，適合小形變區域的配準，不適合大形變的區域配準；當α取值較小時，驅動力較大，收斂速度很快，適合大形變區域的快速配準，但對于小形變區域，則容易產生過矯正的問題，導致圖像的整體配準精度較低.

在實際圖像處理中，尤其是在醫學圖像配準中，兩幀圖像之間通常同時存在大形變和小形變，這導致Active demons算法經常會陷入兩難的境地.綜合以上分析得出，均化系數α調節驅動力無法兼顧大形變和小形變區域的配準.我們應該尋找一種可以解決該問題的方法，使其既能夠兼顧大形變和小形變區域的配準，同時也能夠提高配準精度和收斂速度.

為了提高Demons算法的配準精度，許多學者對Demons算法進行了不同的改進，這些改進算法可以分為3種策略.策略1保證形變場的拓撲保持性.最具代表性的學者是來自法國的Vercauteren等，他們提出了一種標準的配準模型［14-15］，將基于圖像灰度的Demons配準算法看成一個能量優化過程，通過建立一個適當的目標函數，對其進行優化搜索得到相應的配準參數.為了保證形變場的拓撲保持性，避免圖像配準時產生物理上不合理的形變，Vercauteren根據李群理論提出了Diffeomorphic demons配準算法.基于該理論，后人提出了很多的改進算法.例如，Lorenzi等［16］提出在形變場中增加SVFs（Stationary velocity fields）約束和使用新的相似性測度函數LCC（Local correlation coefficient）.另外，林相波等［17］從矢量場的特點出發，詳細分析了該算法得到的形變場拓撲性質，并在此基礎上給出了強化形變場拓撲保持性的方法.策略2是在驅動力計算公式中增加新的信息項，彌補僅依靠灰度梯度信息配準圖像的不足；常見的信息項有灰度梯度場的相似性［18］、對稱正交梯度信息［19］、幾何形狀約束［20］等.策略3從分力的影響程度上開展研究，如Rogelj等［12］提出對稱梯度平均化的Symmetric demons算法；Lin等［21］對兩個分力進行了取舍，如果某個分力指向圖像匹配方向，則對其進行加強，否則將其設為零，取消該分力的影響.文獻［21］中的算法有利于提高配準的精度，但是分力的取舍需要較長的時間.

為了加快配準的收斂速度，Sharp等［22］研究了Demons算法基于硬件的加速方法，利用GPU中的并行計算能力，大幅減少算法運行時間.也有一些學者采用多分辨率策略［21，23］，將低分辨率層的空間變換作為高分辨率層的初始形變矩陣，按照由粗到細的方式進行逐層配準.文獻［24］提出一種在配準迭代過程中采用自適應地調節均化系數的算法.

Pock等［25］及S′anchez等［26］在傳統光流模型的基礎上，利用全變差正則項（Total variation regularization，TV正則項）和魯邦性數據項（L1范數項）構建能量函數得到的TV-L1光流場圖像配準算法的配準精度較高，與Demons類算法相比運算時間縮短不小，但是同樣不能解決大形變的問題.

本文在Active demons算法的基礎上，提出了一種能夠同時提高配準精度和收斂速度的非剛性配準算法.主要思路如下：1）在Active demons算法的驅動力計算公式中引入平衡系數k，該系數聯合均化系數α精細地調整驅動力的強度，使得Active demons算法適合形變范圍更大的圖像配準；2）通過實驗分析，給出平衡系數k的一般取值范圍，增強算法的普適性；3）引入了多分辨率策略.在實驗測試分析中，采用配準精度和收斂速度指標，將提出的算法分別與經典的Active demons配準算法和TV-L1光流場圖像配準算法進行對比.

本文剩余部分結構安排如下：在第1節，本文回顧經典的Demons算法以及Active demons算法；在第2節，介紹本文提出的改進Active demons算法；在第3節，通過對Checkboard測試圖像、自然圖像和醫學圖像的實驗驗證本文算法的有效性；第4節對本文工作進行總結.

1　方法與原理

1.1Demons算法

Demons算法［3］將參考圖像和浮動圖像看成是連續運動圖像序列中的兩幀，并估計從浮動圖像到參考圖像的形變向量u.通常該向量理解為施加在浮動圖像上的形變驅動力.假設圖像在運動的過程中保持灰度不變，對于空間中任意一點（x，y），如果參考圖像S和浮動圖像M上的灰度分別為S（x，y）和M（x，y），?S（x，y）為參考圖像在（x，y）處的梯度值，根據光流場方程可以得到下式：

則 u可以用下式估計：

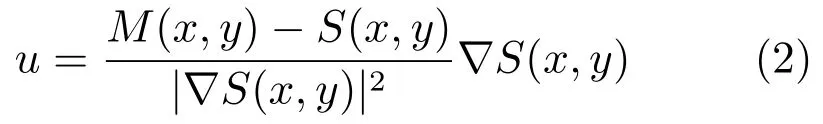
顯然，當|?S（x，y）|2很小時，u可能無限大，與實際情況不符.為了解決該問題，在式（2）分母上增加一新項，變為

式（3）可以保證在參考圖像灰度變化較小的地方對浮動圖像的位移向量 u接近于零，即驅動力為零.

在Demons算法中，采用迭代方式得到最終變換.在第n次迭代時，對每一點（x，y），根據式（3）計算該點的形變驅動力u（x，y），得到該點的瞬時位移vn（x，y）=-un（x，y），計算形變場Tn（p）=Tn-1（p）+vn（p）.此外，為了使該變換在全局范圍內連續，在迭代過程中，使用高斯濾波對瞬時位移進行平滑.

1.2Active demons算法

在Demons算法中，使浮動圖像發生形變的力單純取自參考圖像的梯度信息.這樣的模型只適合于處理小形變問題，不能滿足較大形變圖像配準應用的需要.為了擴大該算法的應用范圍，Wang等［13］根據牛頓第三定律的作用力與反作用力的原理，提出了Active demons算法，將浮動圖像的梯度信息也作為一種正內力引入到驅動力計算公式中，得到下式：

為了能夠調整驅動力的強度，在上式中引入了一個均化系數α，式（4）變為

文獻［27］詳細分析了α的取值對配準結果的影響，該分析結果表明：較小的α可以加快算法的收斂速度，減少配準時間，但配準精度較差；較大的α會增加配準時間，但得到的配準結果較好.

2　基于Active demons算法的非剛性配準方法

2.1一種改進的Active demons算法

本文針對Active demons算法在圖像配準中存在的問題，提出了一種能夠同時提高配準精度和收斂速度的改進算法.在Active demons擴散方程中，為了能夠調節驅動力，Wang在分母中灰度差的平方項上引入了一個均化系數α.受此啟發，將該思想應用在另一分母項上，即在梯度的模值的平方項上引入一個新的系數k，我們稱之為平衡系數.然后通過調整均化系數α和平衡系數k的取值，聯合調節驅動力的強度，較依靠單一系數能夠更加精細地控制配準過程中的的形變程度.改進后的Active demons擴散方程如下所示：

式（6）中，如果均化系數α不變，平衡系數k對驅動力 u的大致影響可以分為三種情況：當k＜1時，分母項減小，u變大，形變程度增大；當k＞1時，分母項增大， u變小，形變程度減小；當k=1時，式（6）等價于Active demons擴散方程的形式.下一節將具體分析平衡系數k的取值對配準結果的影響.

2.2平衡系數的引入及取值分析

2.2.1引入平衡系數的有效性分析

為了清晰地了解參數k對配準結果的影響，本節采用簡單的二值圖像進行配準.如圖1所示，正方形為浮動圖像，圓為參考圖像.實驗參數設置如下：1）圖像分辨率為256×256；2）Demons估計浮動圖像中所有點的形變大小；3）初始形變矩陣為零，空間變換為自由項變換；4）最大迭代次數為200，單尺度實現；5）圖像插值使用三線性插值法.

圖1　二值圖像Fig.1The binary images

為了進行詳細的分析，我們先使用經典的Active demons算法進行配準實驗，均化系數α取10個不同的值，依次為0.05，0.1，0.4，0.5，0.6，1，1.5，2，2.5，3，得到迭代過程的均方差曲線圖，如圖2所示.圖2表明：隨著迭代次數的增加，均方差基本上保持單調遞減，收斂后保持微幅振動.α越小，配準的收斂速度越快，α較大時收斂變慢，但是配準精度更高，這也與文獻［27］的分析相符.

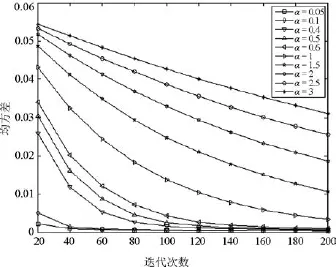
圖2　均化系數α對Active demons算法的影響Fig.2The impact of α on the active demons algorithm

實驗條件不變，采用本文提出的改進Active demons算法進行配準實驗.平衡系數k取0.5，實驗結果的均方差與迭代次數的關系曲線圖如圖3所示.為了比較兩種算法的配準精度，表1為兩種算法迭代200次時得到的均方差（Mean square error， MSE）值.AD為Active demons算法，IAD（Improved active demons）為引入平衡系數k之后的Active demons算法.可以很明顯地看到，IAD算法的均方差值均小于AD算法，這說明改進算法配準精度更高.為了考察收斂速度，分別從兩個實驗中取出4組具有代表性的實驗數據進行對比分析.圖4是兩種算法的配準曲線對比圖，其中，α取為0.05，0.4，1，2，圖4中帶標志的曲線表示Active demons算法，未帶標志的曲線表示改進算法，相同的線型代表相同的均化系數.從曲線圖中可以明顯看到，改進后的Active demons算法的配準曲線與經典的Active demons算法相比更貼近y軸，這說明本文算法的收斂速度更快.

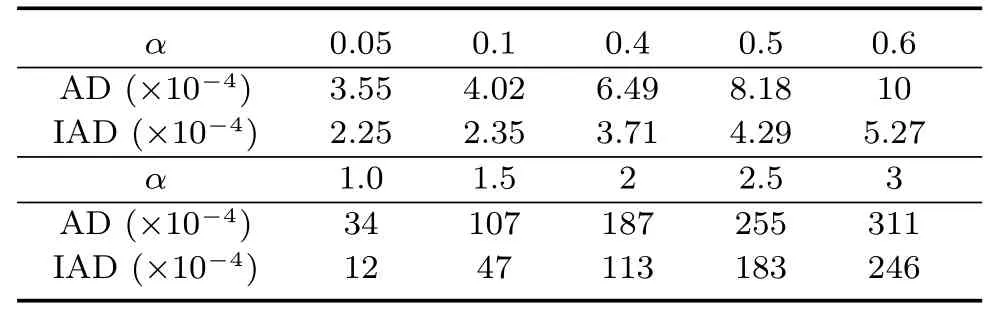
表1　兩種算法的配準結果均方差對比Table 1The comparison of two registration algorithms on the MSE

圖3　均方誤差與迭代次數的關系曲線Fig.3The relations between the mean square error and iterations

以上分析表明：本文在Active demons算法中引入平衡系數k是非常正確的，不僅提高配準的精確度，收斂速度也更快.那么，對于固定的某一均化系數α，該如何確定平衡系數k的值才可使配準性能達到最好呢？接下來，本文將具體分析這個問題.

2.2.2最優平衡系數的取值分析

從理論上分析，在式（6）中，因為|k?S（x，y）|2+ α2（M（x，y）-S（x，y））2≥2αk?S（x，y）（M（x，y）-S（x，y）），所以驅動力的上限為u≤（1/αk）.若α不變， u與k成反比.k越大，u就越小，形變程度小，配準的精度高，但收斂速度較慢.k越小，u越大，允許的形變度越大，收斂速度很快，但配準精度較低.

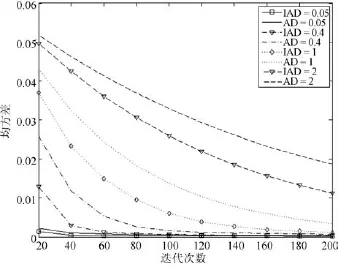
圖4　兩種算法對比曲線Fig.4The comparison of two registration algorithms

在實驗中，設定α為0.5，均化系數k取10個不同的值（0.05，0.1，0.4，0.5，0.6，1.0，1.5，2，2.5，3），考察平衡系數對配準結果的影響，其他實驗條件與上節中相同，結果如圖5～圖7所示.圖5是取不同參數值時的配準結果，圖6是相應的配準結果的差值圖，圖7是配準過程的收斂曲線圖.從圖5和圖6的實驗結果可以明顯看到，在200次迭代條件下，當α取0.5時，k取0.5的配準結果的均方誤差最小，說明配準精度最高；從圖7的曲線圖中可以發現，隨著迭代次數的增加，均方差基本上保持單調遞減，收斂后保持微幅振動.k越小，配準的收斂速度越快；k越大，收斂速度變慢，但是配準精度更高.這也與上面的理論分析相符.

圖5　不同平衡系數k的配準結果Fig.5The registration results with different k variants

圖6　不同參數k的配準結果差值Fig.6The registration results＇error with different k variants

圖8為不同α和k組合情況下，以固定迭代200次之后的配準結果的均方差關系曲面圖，其最小值點位于α=0.5，k=0.5處.從實驗結果中可以看出，α和k較小時，配準精度高平滑性較差；α和k較大時，配準精度相對低.建議二者的取值在［0.5，1.5］之間較適宜.

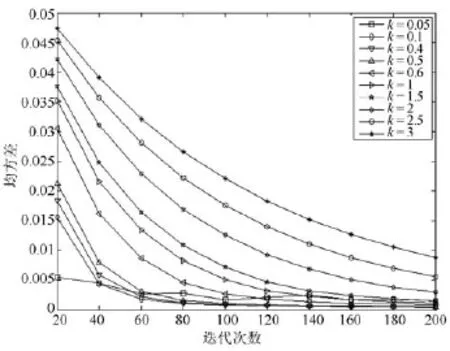
圖7　平衡系數對改進Active demons算法的影響Fig.7The impact of balance coefficient k on the improved active demons registration algorithm

2.3基于多分辨率策略實現

Active demons算法容易陷入局部極小值，而且該算法的運行速度慢、配準精度不高.多分辨率策略可以避免陷入局部極值，在提高算法的準確性、速度和魯棒性方面都很有幫助，其基本思路如下：

1）通過降采樣的方法將待配準圖像分解成多種不同分辨率的圖像；

2）在低分辨率圖像上快速進行粗配準；

3）對在低分辨率圖像上得到的形變場進行升采樣，將其作為更高一級分辨率的初始變換；

4）逐層的迭代，最終實現整幅圖像的配準.

為了進一步提高配準的收斂速度、準確度以及避免陷入局部極值，本文基于多分辨率策略實現，具體實現步驟如下所示.

圖8　均方差與均化系數和平衡系數的關系曲線Fig.8The relations of the mean square error with the α and the k

算法1.基于多分辨率策略實現的配準過程

1：設定初始形變矩陣T0，最大迭代次數k，最大分解尺度L，當前分解級數l，當前迭代次數n；

2：對參考圖像S和浮動圖像M進行L級尺度分解；

3：while（l＜L）do

4：while（n＜N）do

6：n=n+1

7：end while

8：l=l+1，n=0

9：對前一級圖像的形變矩陣Tl-1升采樣，作為當前圖像配準的初始形變矩陣；

10：end while

11：將最終的形變矩陣T應用于浮動圖像M，應用雙三次插值得到配準結果.

3　實驗結果分析

本文先用主觀評價方法對所得配準結果進行分析，并獲得初步的質量評價結果，再用5種客觀評價方法進一步準確地分析配準效果.

為了分析和驗證本文提出算法的實際效果，分別采用測試圖像、自然圖像和醫學圖像進行實驗.實驗中同時采用了Demons算法、Active demons算法（AD）、單尺度實現的改進算法（Single-scale implementation active demons，SIAD）、多分辨率實現的改進算法（Multi-scale implementation active demons，MIAD）和TV-L1光流場算法（TV-L1）.為了公平起見，在下面的實驗中，各種算法的參數選擇都是相對于該算法的最佳結果.

3.1Checkboard測試圖像對比分析

圖9和圖10是針對典型的Checkboard測試圖像的配準實驗，浮動圖像為參考圖像模擬球狀扭曲而得到的，現在欲通過配準將其復原，以此來檢驗各種配準算法的性能.圖9（a）為浮動圖像；圖9（b）為參考圖像；圖9（c）為Demons算法的配準結果；圖9（d）為Active demons算法的配準結果，α為0.5；圖9（e）為SIAD算法的配準結果，α為0.5，k為0.5；圖9（f）為MIAD算法的配準結果，α為0.5，k為0.5，分解尺度為3；圖9（g）為TV-L1光流場算法的配準結果.為了能清晰地分辨配準結果的優劣，圖10為配準后的浮動圖像與參考圖像的差值圖，圖9（a）～（f）分別為原始差值、Demons算法、Active demons算法、SIAD算法、MIAD算法以及TV-L1光流場算法的差值圖.表2為5種算法的配準結果的客觀比較.

通過對比圖9和圖10，可以發現，Demons算法由于僅依靠參考圖像的梯度信息配準圖像，配準結果與參考圖像的誤差最大，配準效果最差；Active demons算法的配準結果相比Demons算法有了一定的改善，尤其是對Demons算法無法配準的大形變區域實現了較好的配準；本文提出的MIAD算法的配準誤差最小，效果最好；SIAD算法的配準結果次之，但也好于原來的兩種配準算法.雖然TV-L1算法配準的效果最好，但其與參考圖像的差值明顯有不規則的邊緣效應.

圖9　圖像的配準結果圖Fig.9The image registration results

圖10　圖像的配準結果與參考圖像的差值Fig.10The differences between the registration results and the static image

從表2的5種客觀評價方法中可以看出，MIAD算法的均方差值最小，相關系數最大，峰值信噪比最大，歸一化互信息最大，結構相似度也是最大的. SIAD算法的5種評價值也均優于Demons算法和Active demons算法，這也與前面的主觀分析一致.綜合以上分析說明，對于測試圖像，無論從配準圖像的主觀效果和客觀指標，顯然目前最新的TVL1光流場算法是最好的，但本文提出的SIAD算法、MIAD算法的配準性能與之非常接近，且好于原來的同類算法.

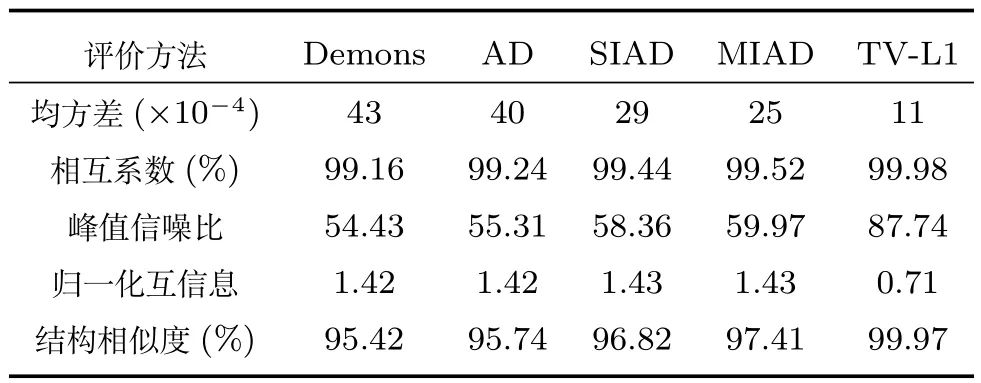
表2　配準結果的客觀分析Table 2The objective analysis of registration results

3.2自然圖像對比分析

下面是針對自然圖像的配準實驗，本文選取兩種不同形變程度的圖像分別進行配準實驗.其中，Lena圖像代表大形變圖像配準，自然彩色圖像代表小形變圖像配準.

圖11和圖12是針對典型的大形變Lena圖像進行的配準實驗.圖11（a）為浮動圖像；圖11（b）為參考圖像；圖11（c）為Demons算法的配準結果；圖11（d）為Active demons算法的配準結果，α為1.5；圖11（e）為SIAD算法配準結果，α為1，k為 1.5；圖11（f）為MIAD算法的配準結果，α為1，k為1.5，分解尺度為3；圖11（g）為TV-L1算法配準結果.圖12為配準后的浮動圖像與參考圖像的差值圖，圖12（a）～（f）分別對應初始差值、Demons算法、Active demons算法、SIAD算法、MIAD算法和TV-L1算法的差值圖.表3為5種算法的配準結果的客觀比較.

從圖11和圖12的配準結果差值圖中可以明顯看出，Demons算法完成了圖像中小形變部分的配準，在一定程度上糾正了浮動圖像中面部五官的形變，但頭發部位的形變加強了，眉毛和帽子也發生了畸變；Active demons算法相比Demons算法在處理大形變圖像配準問題上優越性明顯，尤其是頭發部位的矯正.但對于形變較小的四周區域，在經過了Active demons算法配準之后，明顯形變過大；SIAD算法不僅解決了Active demons算法存在的小形變區域過配準的問題，而且保留了大形變區域配準的準確性，配準誤差更小，MIAD算法的配準誤差最小，配準的差值圖很光滑，證明了多分辨率策略實現的優越性.從配準圖像及與參考圖像的差值來看，TV-L1算法配準的效果是最好的，但其差值圖邊緣具有不規則的邊緣效應.

從表3中的5種客觀評價方法可以看出，對于TV-L1光流場算法，除了均方誤差指標不及本文提出的算法外，其他的指標都是最好的.同理，對于本文提出的算法，除了TV-L1外，其5個指標均優于其他同類算法，特別是結構相似度，比其他算法都高出很多.這也進一步表明了本文算法優越性，能夠較好地保持圖像的拓撲結構.

圖13是針對小形變的彩色自然圖像進行的配準實驗，浮動圖像只出現了局部小形變.圖13（a）為浮動圖像；圖13（b）為參考圖像；圖13（c）為Demons算法的配準結果；圖13（d）為Active demons算法的配準結果，α為2；圖13（e）為SIAD算法配準結果，α為0.5，k為1.5；圖13（f）為MIAD算法的配準結果，α為0.5，k為1.5，分解尺度為3；圖13（g）為TV-L1算法配準結果.由于該測試圖像是彩色小形變圖像，圖像的信息豐富，由5種配準算法得到的配準圖像的配準精度都較高，從圖13中的各種算法配準結果很難能夠辨別出差異；同樣，由這些算法得到的配準圖像與參考圖像的差值圖，依靠肉眼觀察差異性較小，整體背景將是黑色，所以這里就不把這些差值圖列出來.我們可以依靠表4中5種算法的配準結果的客觀指標比較進行評判.

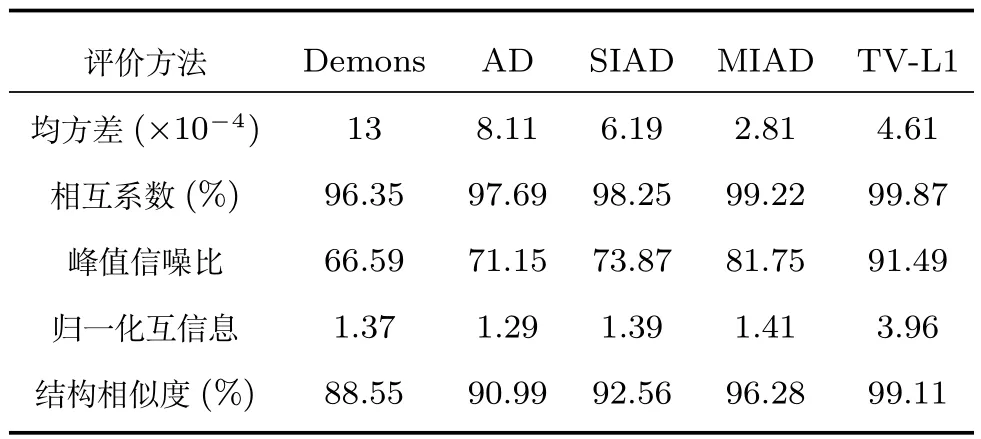
表3　配準結果的客觀分析Table 3The objective analysis of registration results

從表4中的5種客觀指標（R、G、B彩色通道分列）可以看出，Demons算法、Active demons算法、SIAD算法、TV-L1算法的配準均方誤差均明顯小于MIAD算法的配準均方誤差.但整體來講，這5種算法的其余4個客觀指標基本相當，這說明對于小形變的彩色自然圖像，本文提出的SIAD算法與Demons算法、Active demons算法的效果基本等價，且提出的MIAD算法不如Demons算法、Active demons算法和SIAD算法要好，這主要是由于Demons算法、Active demons算法本身擅長小形變區域的配準.由于采用的測試圖像是變形小的彩色圖像，且信息量豐富，MIAD算法的優勢顯現不出來.主要原因是由于圖像形變太小，呈現不出MIAD算法的優勢.

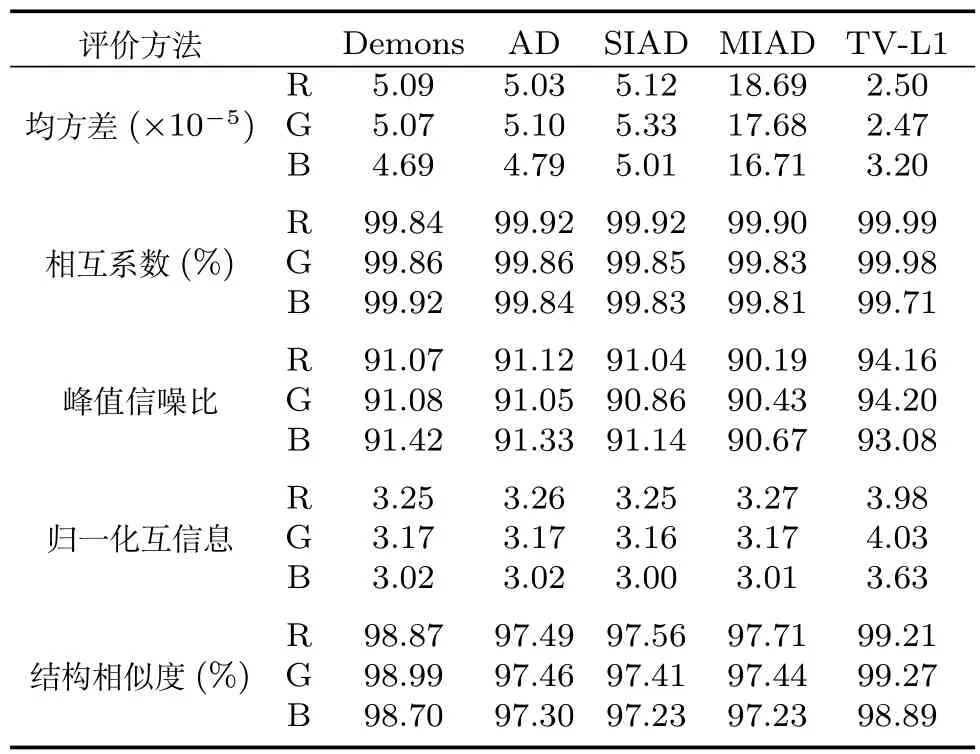
表4　配準結果的客觀分析Table 4The objective analysis of registration results

圖11　圖像的配準結果圖Fig.11The image registration results

圖12　圖像的配準結果與參考圖像的差值Fig.12The differences between the registration results and the static image

圖13　圖像的配準結果圖Fig.13The image registration results

3.3醫學圖像的對比分析

為了考察5種算法在醫學圖像上的配準性能，本節進行了2組試驗.前1組是來源于網絡檢驗配準算法優劣的常用實驗數據，代表小形變圖像配準的測試.后1組為真實的實驗數據，為磁共振肝圖像的位置矯正實驗，代表大形變圖像配準的測試.

圖14和圖15是對醫學圖像的小形變配準實驗.圖14（a）為參考圖像；圖14（b）為浮動圖像；圖14（c）為Demons算法的配準結果；圖14（d）為Active demons算法的配準結果，α為2；圖14（e）為SIAD算法的配準結果，α為0.5，k為2；圖14（f）為MIAD算法的配準結果，α為0.5，k為2，分解尺度為3；圖14（g）為TV-L1算法配準結果.圖15為配準后的浮動圖像與參考圖像的差值圖，表6為5種算法的配準結果的客觀比較.

通過視覺觀察圖14和圖15可以發現，Demons算法的配準效果比Active demons算法要好；Active demons算法單純依靠均化系數調節形變程度，會導致小形變區域矯正過大，產生誤配準的問題；SIAD算法的配準誤差相比Active demons算法和Demons算法明顯減少，差值圖更平滑；基于多分辨率策略實現的MIAD算法的配準差值圖總體比較平滑，沒有出現較大的配準誤差區域.TV-L1算法的配準差值圖是最平滑的，但表6中其均方誤差及峰值信噪比要次于MIAD算法.

從表5的5種客觀評價方法可以看出，Active demons算法的各項客觀評價指標確實不如Demons算法，配準性能最差，這也與前面的視覺觀察相呼應.除了TV-L1的歸一化互信息最高外，MIAD算法的其他4種客觀評價指標最好，所以配準效果相對最優.

肝癌患者接受分次放射治療的過程中，治療部位的位置和形狀可能發生變化，靶區形狀以及靶區與周圍危及器官的位置關系也會發生變化，因此需要利用圖像配準技術來跟蹤形變［27］.圖16和圖17是采用真實的磁共振肝圖像進行的配準實驗.圖16（a）為參考圖像；圖16（b）為浮動圖像；圖16（c）為Demons算法的配準結果；圖16（d）為Active demons算法的配準結果，α為1；圖16（e）為SIAD算法的配準結果，α為0.4，k為1.5；圖16（f）為MIAD算法的配準結果，α為0.5，k為2，分解尺度為3；圖16（g）為TV-L1算法配準結果.圖17為5種算法的配準結果與參考圖像的差值圖，表7為5種算法的配準結果的客觀比較.

從圖16和圖17中可以看出，TV-L1算法的配準效果是最好的；Demons算法對于圖像中部的大形變區域與參考圖像存在很大的偏差；Active demons算法比Demons算法有了一定程度的改善，但在輪廓的小形變區域里出現了明顯的誤配準現象；SIAD算法相比Active demons算法，配準誤差減小了很多；MIAD算法得到的配準效果最好，無論是對大形變區域還是小形變區域，均實現了準確的配準.表6的客觀分析驗證了前面的主觀分析，TV-L1算法是最好的，MIAD算法其次，進一步說明了本文提出的算法相比原來的算法在醫學圖像配準應用上更有優勢.

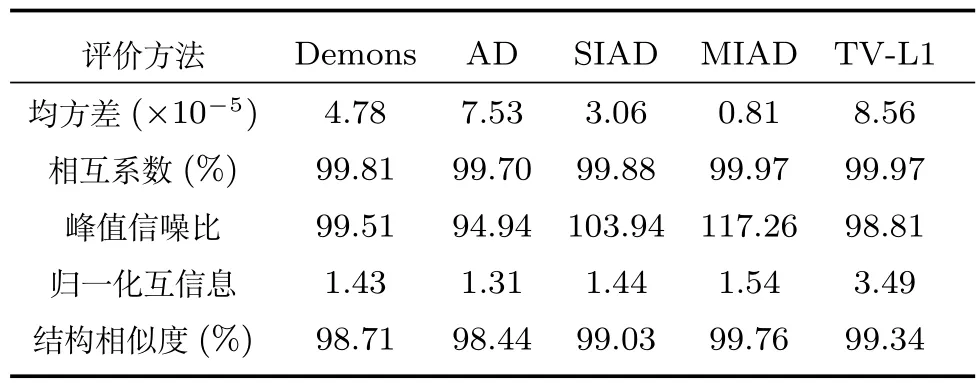
表5　配準結果的客觀分析Table 5The objective analysis of registration results

表6　配準結果的客觀分析Table 6The objective analysis of registration results

為了衡量某種算法在配準精度方面優于其他算法的程度，文獻［18］定義了Pe來權衡，計算公式如下：

其中，MSEe為已有的配準算法的均方差，MSEp為提出算法的均方差.

圖14　圖像的配準結果圖Fig.14The image registration results

圖15　圖像的配準結果與參考圖像的差值圖Fig.15The differences between the registration results and the static image

圖16　圖像的配準結果圖Fig.16The image registration results

圖17　圖像的配準結果與參考圖像的差值圖Fig.17The differences between the registration results and the static image

本文也采用上面的方法來衡量提出的算法在配準精度上的優越性.由于Demons算法的配準精度不如Active demons算法，所以本文僅與Active demons算法相比較.關于實驗結果的精確度分析如表7所示，其中最后兩列表示本文提出的兩種算法相對于Active demons算法在配準精確度上的提高程度，經過計算分別平均提高了28.45%、54.28%.

4　結束語

針對Active demons算法存在的問題，本文提出了一種改進算法.經過在Checkboard測試圖像、自然圖像和醫學圖像上的實驗表明，本文算法的圖像配準精確度要好于Active demons算法、Demons算法，接近于最新的TV-L1光流場配準算法，配準的速度較Active demons算法和Demons算法大大提高，但不如TV-L1光流場配準算法快.對于相對大形變圖像的配準，改進算法解決了Active demons算法可以配準大形變區域而無法兼顧小形變區域的配準問題.對于小形變圖像的配準，改進算法提高了Active demons算法的配準精度，實現了小形變區域的更準確的配準.所以本文提出的算法比經典的Active demons算法更有優勢，是一種有效的處理非剛性配準的方法.

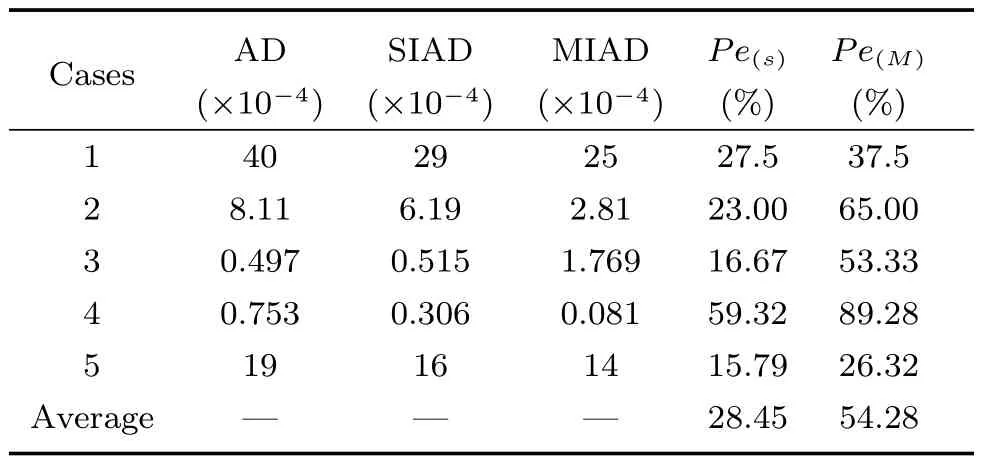
表7　幾種算法的配準結果均方差值比較Table 7The objective analysis of difference algorithms

應該說無論是TV-L1光流場配準算法、Demons算法、Active demons算法，還是本文提出的新算法都是基于灰度信息的，針對小形變的圖像配準有明顯效果，相對大形變的圖像還有基于圖像特征的配準算法有優勢.盡管如此，本文算法也存在如下不足.由于改進算法引入了新參數，在進行配準實驗時，為了達到高配準精度，針對不同的圖像類型，可能需要進行一定的參數取值試驗工作，以選擇最優的配準結果.

References

1 Sotiras A，Davatzikos C，Paragios N.Deformable medical image registration：a survey.IEEE Transactions on Medical Imaging，2013，32（7）：1153-1190

2 Cachier P，Pennec X，Ayache N.Fast non rigid matching by gradient descent：study and improvements of the“Demons”algorithm.Technical Report-3706，India，1999.

3 Thirion J P.Image matching as a diffusion process：an analogy with Maxwell＇s demons.Medical Image Analysis，1998，2（3）：243-260

4 Brown L G.A survey of image registration techniques.ACM Computing Surveys，1992，24（4）：325-376

5 Lester H，Arridge S R.A survey of hierarchical non-linear medical image registration.Pattern Recognition，1999，32（1）：129-149

6 Jie T，Xue J，Dai T K，Chen J，Zheng J.A novel software platform for medical image processing and analyzing.IEEE Transactions on Information Technology in Biomedicine，2008，12（6）：800-812

7 Cao Z L，Dong E Q，Zheng Q，Sun W Y，Li Z Z.Accurate inverse-consistent symmetric optical flow for 4D CT lung registration.Biomedical Signal Processing and Control，2016，24：25-33

8 Cao Z L，Dong E Q.Distinctive local binary pattern for non-rigid registration of lung computed tomography images. Electronics Letters，2015，51（22）：1742-1744

9 Nithiananthan S，Schafer S，Mirota D J，Stayman J W，Zbijewski W，Reh D D，Gallia G L，Siewerdsena J H.Extradimensional demons：a method for incorporating missing tissue in deformable image registration.Medical Physics，2012，39（9）：5718-5731

10 Reaungamornrat S，Wang A S，Uneri A，Otake Y，Khanna A J，Siewerdsen J H.Deformable image registration with local rigidity constraints for cone-beam CT-guided spine surgery. Physics in Medicine and Biology，2014，59（14）：3761-3787

11 Hellier P，Barillot C，Corouge I，Gibaud B，Le Goualher G，Collins D L，Evans A，Malandain G，Ayache N，Christensen G E，Johnson H J.Retrospective evaluation of intersubject brain registration.IEEE Transactions on Medical Imaging，2003，22（9）：1120-1130

12 Rogelj P，Kovaˇciˇc S.Symmetric image registration.Medical Image Analysis，2006，10（3）：484-493

13 Wang H，Dong L，O＇Daniel J，Mohan，Garden A S，Ang K K，Kuban D A，Bonnen M，Chang J Y，Cheung R.Validation of an accelerated‘demons’algorithm for deformable image registration in radiation therapy.Physics in Medicine and Biology，2005，50（12）：2887-2905

14 Vercauteren T，Pennec X，Perchant A，Ayache N.Nonparametricdiffeomorphicimageregistrationwiththe demons algorithm.In：Proceedings of 10th International Conference on Medical Image Computing and Computer-Assisted Intervention（MICCAI 2007）.Brisbane，Australia，2007.319-326

15 Vercauteren T，Pennec X，Perchant A，Ayache N.Diffeomorphic demons：efficient non-parametric image registration.NeuroImage，2009，45：S61-S72

16 Lorenzi M，Ayache N，Frisoni G B，Pennec X.LCC-Demons：a robust and accurate symmetric diffeomorphic registration algorithm.NeuroImage，2013，81：470-483

17 Lin Xiang-Bo，Qiu Tian-Shuang，Ruan Su，Nicolier F.Research on the topology preservation of the demons nonrigid registration algorithm.Acta Automatica Sinica，2010，36（1）：179-183（林相波，邱天爽，阮素，Nicolier F.Demons非剛性配準算法拓撲保持性的研究.自動化學報，2010，36（1）：179-183）

18 Liu X Z，Yuan Z M，Zhu J M，Xu D R.Medical image registration by combining global and local information：a chaintype diffeomorphic demons algorithm.Physics in Medicine and Biology，2013，58（23）：8359-8378

19 Lu C，Mandal M.Improved image registration technique based on demons and symmetric orthogonal gradient information.In：Proceeding of the 2010 International Conference on Signal Processing and Communications（SPCOM）.Bangalore：IEEE，2010.1-5

20 Cazoulat G，Simon A，Dumenil A，Gnep K，de Crevoisier R，Acosta O，Haigron P.Surface-constrained nonrigid registration for dose monitoring in prostate cancer radiotherapy.IEEE Transactions on Medical Imaging，2014，33（7）：1464-1474

21 Lin X B，Qiu T S，Nicolier F，Ruan S.An improved method of‘Demons’non-rigid image registration algorithm.In：Processing of the 9th International Conference on Signal Processing.Beijing，China：IEEE，2008.1091-1094

22 Sharp G C，Kandasamy N，Singh H，Folkert M.GPU-based streaming architectures for fast cone-beam CT image reconstruction and demons deformable registration.Physics in Medicine and Biology，2007，52（19）：5771-5783

23 Guimond A，Roche A，Ayache N，Meunier J.Threedimensional multimodal brain warping using the demons algorithm and adaptive intensity corrections.IEEE Transactions on Medical Imaging，2001，20（1）：58-69

24 Xu Sheng-Zhou，Song En-Min，Xu Xiang-Yang.Non-rigid mammogram registration based on improved demons algorithm.Journal of Image and Graphics，2009，14（12）：2566-2571（徐勝舟，宋恩民，許向陽.基于改進Demons算法的乳腺X線攝片非剛性配準.中國圖象圖形學報，2009，14（12）：2566-2571）

25 Pock T，Urschler M，Zach C，Beichel R，Bischof H.A duality based algorithm for TV-L1-optical-flow image registration.In：Proceedings of the 10th International Conference on Medical Image Computing and Computer Assisted Intervention（MICCAI）.Brisbane，Australia：Springer，2007. 511-518

26 S′anchez J，Meinhardt-Llopis E，Facciolo G.TV-L1 optical flow estimation.Image Processing on Line，2013，3：137-150

27 Lin Xiang-Bo，Qiu Tian-Shuang，Nicolier F，Ruan Su.The study of active demons algorithm for deformable image registration.Chinese Journal of Biomedical Engineering，2008，27（4）：636-640（林相波，邱天爽，Nicolier F，Ruan Su.Active Demons可變形圖像配準算法研究.中國生物醫學工程學報，2008，27（4）：636-640）

薛鵬山東大學（威海）碩士研究生. 2015年獲得哈爾濱工程大學工學學士學位.主要研究方向為醫學圖像處理.

E-mail：xuepeng2016@126.com

（XUEPengMasterstudentat Shandong University（Weihai）.He received his bachelor degress from Harbin Engineer University in 2015.His main research interest is medical image processing.）

楊佩山東大學（威海）碩士研究生. 2008年獲得山東大學（威海）學士學位.主要研究方向為醫學圖像處理.

E-mail：yangpei301@163.com

（YANGPeiMasterstudentat Shandong University（Weihai）.She received her bachelor degree from Shandong University（Weihai）in 2008.Her main research interest is medical image processing.）

曹祝樓山東大學（威海）數學與統計學院講師.2015年獲得山東大學（威海）博士學位.主要研究方向為圖像處理.

E-mail：zlouc@sdu.edu.cn

（CAO Zhu-LouLecturer at the Institute of Mathematics and Statistics，Shandong University（Weihai）.He received his Ph.D.degree from Shandong University（Weihai）in 2015.His main research interest is image processing.）

賈大宇山東大學（威海）碩士研究生，2013年獲得哈爾濱工業大學學士學位.主要研究方向醫學圖像處理.

E-mail：dayu_jia1990@126.com

（JIADa-YuMasterstudentat Shandong University（Weihai）.He received his bachelor degree from Harbin Institute of Technology in 2013.His main research interest is medical image processing.）

董恩清山東大學（威海）教授.2002年于西安交通大學獲得信息與通信工程專業博士學位.主要研究方向包括無線通信技術，無線傳感器網絡，醫學圖像處理.本文通信作者.

E-mail：enqdong@sdu.edu.cn

（DONG En-QingProfessor at the Shandong University（Weihai）.He received his Ph.D.degree from Xi＇an Jiaotong University in 2002.His research interest covers wireless communication network technology，wireless sensor networks，and medical image processing.Corresponding author of this paper.）

Active Demons Non-rigid Registration Algorithm Based on Balance Coefficient

XUE Peng1YANG Pei1CAO Zhu-Lou1JIA Da-Yu1DONG En-Qing1

Classic active demons algorithm uses gradient information of the static image and the moving image as driving forces，and uses a homogeneous coefficient to adjust their intensities.Although the algorithm overcomes the disadvantage of the demons algorithm using the gradient information of a single static image，the homogeneous coefficient of the active demons algorithm can not accurately handle registration with both large deformation and small deformation，and will cause the mutual restraint problem of convergence speed and registration accuracy.In order to solve this problem，this paper presents a non-rigid registration algorithm based on active demons algorithm，which introduces a new parameter called balance coefficient to the active demons algorithm to adjust the driving force in combination with the homogeneous coefficient.Not only can the large deformation and small deformation be taken into account at the same time，but also the mutual restraint problem of speed and accuracy can be eased to a certain extent.In order to further improve registration accuracy and convergence speed and avoid falling into local extremes，a coarse-to-fine multi-resolution strategy is introduced into the registration process.Experiments on checkboard test images，natural images and medical images demonstrate that the proposed algorithm is faster and more accurate.The registration accuracy is improved by 54.28% on average，and is close to that of the latest TV-L1 optical flow image registration algorithm.

Non-rigid image registration，active demons algorithm，optical flow image registration，driving force，multiresolution strategy

Manuscript April 22，2015；accepted March 20，2016

10.16383/j.aas.2016.c150186

Xue Peng，Yang Pei，Cao Zhu-Lou，Jia Da-Yu，Dong En-Qing.Active demons non-rigid registration algorithm based on balance coefficient.Acta Automatica Sinica，2016，42（9）：1389-1400

2015-04-22錄用日期2016-03-20

國家自然科學基金（81371635），高等學校博士學科點專項科研基金（20120131110062），山東省科技發展計劃項目（2013GGX10104）

Supported by National Natural Science Foundation of China（81371635），Specialized Research Fund for the Doctoral Program of Higher Education of China（20120131110062），Science and Technology Development Project of Shandong Province（2013GGX10104）

本文責任編委楊健

Recommended by Associate Editor YANG Jian

1.山東大學（威海）機電與信息工程學院威海264209

1.School of Mechanical，Electrical&Information Engineering，Shandong University，Weihai 264209