基于客流的有軌電車發車時刻模型研究

巴宇航　姜　梅　郭孜政　陳崇雙

(1. 西南交通大學交通運輸與物流學院　成都　610031；2. 中國中鐵二院工程集團有限責任公司科學技術研究院　成都　610031；3. 西南交通大學數學學院　成都　611756)

?

基于客流的有軌電車發車時刻模型研究

巴宇航1姜梅2郭孜政1陳崇雙3

(1. 西南交通大學交通運輸與物流學院成都610031；2. 中國中鐵二院工程集團有限責任公司科學技術研究院成都610031；3. 西南交通大學數學學院成都611756)

闡明國內現有對公共交通發車時刻表的研究模型計算復雜，未考慮影響運營的多重因素，針對城市有軌電車系統，提出一種以車站客流量為依據、不均勻的發車時刻模型。首先以有軌電車最大、最小滿載率和發車間隔作為約束，兼顧運營企業收入與有軌電車系統對乘客的服務水平；然后以斷面客流作為確定發車間隔的依據，得到有軌電車的全天發車時刻表；最后通過影響發車的隨機波動因素對發車時刻進行校正。該方法在實踐中較以往的方法更加容易執行。

有軌電車；發車時刻；客流；滿載率；發車間隔

現代城市有軌電車系統具有良好的適用性與經濟性[1]，因此在大中型城市得到廣泛利用。有軌電車運營調度的基礎是制訂合理的發車時刻表，時刻表的制訂對電車發車計劃與折返計劃的制訂與實施具有重要影響。

目前，國內對于公共交通發車時刻表的研究主要有以下兩類：一類是研究基于各種智能的優化算法，代表性研究有王慶榮[2]、陳遠[3]等人將遺傳算法引入到公交排班問題的研究中，并對模型進行優化求解；另一類是研究基于實際運營調度的影 響 因 素，代 表 性 研 究有李英帥[4]等人依據客流在時間上的不均衡性優化了發車間隔，熊桂喜[5]等人建立了支持信號優先的快速公交行車時刻表優化模型，從而降低了車輛在交叉口的等待時間。

上述研究從不同層面完善了公交時刻表的制訂研究，但仍存在一定不足：1) 智能優化算法比較復雜，求解困難；2) 對于發車時刻的制訂未兼顧運營企業收入與公交系統對乘客提供的服務水平。鑒于以上不足，筆者提出一種基于客流并兼顧公交運營收入與乘客服務水平的有軌電車發車時刻模型，以期得到一種以客流量為基礎，考慮多重運營因素的時刻表算法。

1　有軌電車時刻表制訂影響因素分析

以客流數據、運營企業收入、有軌電車系統對乘客的服務水平以及影響發車間隔的隨機波動因素作為制訂有軌電車發車時刻表的依據。

乘客的活動具有規律性與周期性，具體表現在時間與空間上。客流在時間上具有不均衡性，早晚高峰的客流量比平峰要高，商業區的客流量在節假日比工作日要高[4]；在空間上，上下行不同站點的客流量不同，即客流同時具有空間不均衡性，這是由于客流量大小易受周邊土地開發與經濟發展情況的影響。在實際的運營過程中，只有適應客流實際時間、空間分布規律的時刻表方案，才可為乘客提供高質量的服務水平。

時刻表的制訂應同時考慮運營企業收入與有軌電車系統的服務水平，即需平衡公交乘客和公交企業的利益，使兩者盡量達到最大化[6]。時刻表發車間隔制訂過密，易造成系統資源浪費，不利于運營企業的盈利與組織；發車間隔制訂過大，易造成乘客等待時間過長和車內滿載過高，會對有軌電車系統的整體服務水平產生不利影響。因此，發車間隔的制訂應在考慮客流時空特征的基礎上，綜合上述兩因素，具體通過發車時刻模型的約束條件進行界定。

由于現代城市有軌電車使用專用車道，因此影響發車的隨機波動因素主要為電車在各站點、交叉口的等待時間。等待時間的大小由客流量大小、線路有無突發事件、交叉口的控制機制而確定。下面的算法以客流為基礎，在制訂發車時刻模型中還應考慮電車在交叉口的等待時間。

2　有軌電車發車時刻模型算法設計

2.1時刻表模型假設

1) 只考慮1條線路，共m個車站(i∈m)，對稱設置在線路上下行方向。假設相鄰車站之間只有1個交叉口，則整條線路共(m-1)個交叉口(j∈m-1)，電車在每個交叉口的停車時間為t1(j)；

2) 已知不同日期、時段、站點的客流數據，對應實際情況，已知高平峰時段的劃分；

3) 車輛在線路上勻速行駛，行駛速度為v；

4) 有軌電車運營時間[tb,te]；

5) 每班電車編組數量、車輛型號一致。

2.2時刻表模型約束

2.2.1最大、最小發車間隔約束

考慮到乘客的等待時間與有軌電車系統能力，對相鄰班次電車的發車間隔進行約束，即第k班和第k+1班電車的發車間隔在約束間隔時間以內，有

(1)

式中，t(k)為第k個班次在始發站的發車時刻。

2.2.2滿載率的約束

考慮到乘客的舒適程度及運營企業的效益，對每班電車的滿載率進行約束，有

ρmin≤ρi(k)≤ρmax

(2)

式中，ρi(k)為第k個班次在第i站的車輛滿載率(i≤m)；ρmin為電車最低滿載率；ρmax為電車最高滿載率。

2.3時刻表模型建立

采集該線路上某一天不同時段站點的上、下車人數，按照以下步驟建立發車時刻表模型。

2.3.1建立凈上車人數曲線

將每一站的上、下車人數等間隔按照統計時段采樣，通過數據擬合得到該站全天凈上車人數關于時間的分布曲線o(i,t)，則在[t1,t2]時段內，第i站的凈上車人數為

(3)

凈上車人數有時會出現負的情況，負的實際意義是在統計的[t1,t2]時段內，下車人數多于上車人數。

2.3.2電車在車站的計劃停車等待時間

時刻表的制訂需在初期計劃每班電車在車站的等待時間。依據有軌電車運營時間內的上車人數，劃分車站等級，不同等級的車站，計劃電車在車站有不同的停站等待時間t2(i)。車輛在車站的停車時間視車站乘客數量多少而定。一般情況下，高峰時段由于乘客數量較多，停車時間較長；反之，平峰時段停車時間較短。

(4)

式中，t1,t2,…,tp為電車在不同等級車站的停站等待時間，t1>t2>…>tp；a1,a2,…，ap為車站的候車乘客數量，a1>a2>…>ap。

由此，將車站劃分為p個等級，對不同等級的車站在調度初期就預留不同的停站時間，這樣有利于合理分配發車間隔。

2.3.3客流平移與疊加

在通常的客流數據處理中，往往把各個站點調查的實際時間的數據作為調度的依據，忽略了車輛的行車時間對疏散客流的影響[7]。為此，筆者提出將客流曲線按時間平移的數據處理方法，將始發站之外的所有車站的客流全部平移疊加到始發站。

第i站到第i+n站的行駛時間為

(5)

其中，n=1,2,…,m-i。

那么當電車行駛到第i站(共行駛過j個交叉口，j=i-1)的延遲時間為

(6)

式中，t1(j)為電車在第j個交叉口的等待時間，則將第i站凈上車人數分布曲線平移到始發站的曲線為

o’(i,t)=o(i,t+ty(i))

(7)

其中，2≤i≤m。

將所有車站凈上車人數疊加到始發車站的分布曲線為

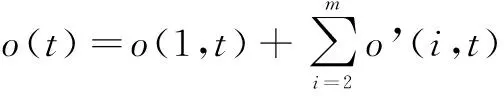
(8)

即客流凈上車人數疊加曲線為始發站上車人數曲線與其余所有車站平移到始發站的累加曲線之和。

2.3.4確定發車間隔

依據不同的約束條件，求得每兩個相鄰班次的發車間隔，從而得到運營時間內所有班次的發車時刻。

已知第k個班次的發車時刻t(k)，那么發車后由于電車滿載，車站上的滯留乘客數量為

(9)

式中，r(k)為第k班電車開走后車站的滯留乘客；lmax為電車達最高滿載率時的載客量。

由此，可以由公式(10)、(11)計算得到第k班電車發車后第k+1班電車在達到最低、最高滿載的時刻tu(k+1)、tv(k+1)。

(10)

式中，tu(k+1)為第k+1班電車達到最低滿載時的發車

時刻；lmin為電車達最低滿載率時的載客量。

(11)

式中，tv(k+1)為第k+1班電車達到最高滿載時的發車時刻；lmax為電車達最高滿載率時的載客量。

在高峰、平峰不同時段內，根據系統對斷面客流的運載能力，設置計劃發車間隔時間Δt。計劃發車間隔的設置應盡量滿足該時段內電車發車的班次對所有車站中最大斷面客流的運輸，一般平峰時段間隔大于高峰時段間隔。

以平峰時段[ta,tb]為例進行說明，統計該時段客流量最高的車站，以系統能力滿足該斷面客流設置計劃發車間隔，有

(12)

Δt=(tb-ta)/nta,tb

(13)

式中：nta,tb為在[ta,tb]時段內的計劃發車數目；ρ為電車運營計劃滿載率，一般通過考慮電車計劃營業收入與對乘客的服務水平來確定；W為電車額定載客人數。

根據約束條件，得到第k+1班電車的發車時刻，有

(14)

對于公式(14)的解釋為：按預定發車間隔的發車時刻早于最低滿載發車時刻，則按照最低滿載發車時刻發車；若晚于最高滿載發車時刻，則按最高滿載發車時刻發車；若在兩個滿載發車時刻之間，則按照預定發車間隔的發車時刻發車。當發車間隔超出最大、最小發車間隔范圍時，根據超出的限界(超出的是最大或最小間隔)，選擇最大或最小發車間隔作為發車間隔。

由此，在已知最早發車時刻的基礎上，只需依據條件與約束依次計算下一班次的發車時刻，即可得到全天所有班次的發車時刻。

2.3.5基于交叉口等待時間的發車間隔校正

電車在交叉口的等待時間由電車到達交叉口的時刻與交叉口的控制機制決定，有

(15)

t(j,k)=min{tg(j)-t′(j,k)}

(16)

式中：t(j,k)為第k班電車在交叉口j的等待時刻；t(j,k)≥0，tg(j)為交叉口j的綠燈啟亮時刻；t′(j,k)為第k班電車到達交叉口j的時刻。

將公式(16)帶入公式(6)，繼而可以重新計算電車的運行延遲時間，從而根據公式(7)～(14)可以得出經修正后的下一班次的發車時刻。

3　結語

本文以有軌電車車站斷面客流量為依據，構建了一套有軌電車時刻表制訂方法，主要研究成果有：將運營企業收入與有軌電車系統對乘客的服務水平兩種因素量化到模型的約束條件中，使時刻表的制訂兼顧上述兩種因素，更加合理；通過約束條件確定發車間隔，從而得到全天發車時刻表，該方法在實踐中較 已 有 研究方法更加容易執行。相對本研究，有軌電車在交叉口的等待與優先機制將是下一步研究的重點。

[1] 崔亞南.現代有軌電車應用模式及區域適用性評價研究[D].北京：北京交通大學,2012.

[2] 王慶榮,袁占亭,張秋余.基于改進遺傳—模擬退火算法的公交排班優化研究[J].計算機應用研究,2012(7):2461-2463.

[3] 陳遠.基于遺傳算法的公交智能排班方法的研究[J].智能計算機與應用,2012(5):75-77.

[4] 李英帥,孫連超,張旭,等.基于時間客流不均衡性公交發車間隔優化方法[J].交通科技與經濟,2011(6):89-92.[5] 熊桂喜,馬樹東.支持信號優先的快速公交行車時刻表優化算法[J].計算機與信息技術,2008(S1):12-14.

[6] 宋瑞,何世偉,楊永凱,等.公交時刻表設計與車輛運用綜合優化模型[J].中國公路學報,2006(3):70-76.

[7] 覃運梅.城市公交調度優化方法研究[D].合肥：合肥工業大學,2006.

(編輯：曹雪明)

Research on Tram Dispatching Time Model Based on Passenger Flow

Ba Yuhang1Jiang Mei2Guo Zizheng1Chen Chongshuang3

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031; 2. Research Institute of Science and Technology, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031; 3. School of Mathematics, Southwest Jiaotong University, Chengdu 611756)

Present domestic studies on the operation of public transportation dispatching time proposed very complicated algorithms and ignored the influence arising from multiple factors. Against this background, an uneven dispatching time model for tram system based on traffic flow is offered in this paper. Firstly, the model is subjected to the maximum and minimum passenger load and dispatching intervals which gives consideration to the operation company's income and the level of passenger service, then the dispatching interval is determined by the traffic flows over a station segment and the dispatching time in a whole day is worked out. Finally, the tram dispatching time model is corrected by the random fluctuations which affect tram dispatching. The method can be implemented easily compared with other methods.

tram; dispatching time; passenger flow; passenger load; dispatching interval

10.3969/j.issn.1672-6073.2016.01.010

2015-01-22

2015-04-02

巴宇航，女，碩士研究生，主要從事交通規劃、交通運輸安全研究，bayuhangedu@163.com

四川省科技計劃項目(2014GZ0081)

U491.1

A

1672-6073(2016)01-0038-04