語言互譯，有效轉化——淺談2016年常州中考數學第18題的命制

劉蔣巍

學思堂教育研究院

語言互譯，有效轉化——淺談2016年常州中考數學第18題的命制

劉蔣巍

學思堂教育研究院

筆者對2016年常州中考數學試題進行了深入研究與思考，現將2016年常州中考數學卷第18題的命制過程從“語言互譯，有效轉化”的角度與各位同仁分享，并將“語言互譯”在教學中的運用給出范例。

常州中考數學；語言互譯；有效轉化

一、語言互譯，有效轉化

試題命制、打磨的方法有很多，文［1］給出了試題變式的兩種常用方法。但試題的打磨除了對條件的加強與弱化之外，我們還可以從數學語言的角度進行轉譯，將直接表達轉為間接表達，使問題的本質得到隱藏，從而增加試題的難度。以2016年常州中考數學卷第18題為例，命制過程如下：

（1稿）在ΔAPB中，AB=2，∠APB=90°，則ΔAPB面積的最大值為______

思路：以AB為直徑構造輔助圓。

點評：該問題若出在單元檢測中，對于初學者而言，有一定的區分度。但對于中考學生經過單元檢測，一輪復習，二輪復習后，這樣的難度顯然起不到壓軸的作用。命題組對1稿進行修改。

（2稿）如圖，ΔAPB中，AB=2，∠APB=90°，在AB的同側作正ΔABD、正ΔAPE和正ΔBCP，則四邊形PCDE面積的最大值是_____

延長CP交AE于點F，易得PF⊥AE

由題設條件，易證四邊形PCDE為平行四邊形，其面積為PC·EF，即PE·PC，亦即PA·PB，即ΔAPB面積，最大值為1。

二、“語言互譯”在變式教學中的運用

筆者運用“語言互譯”的試題打磨方法，對2016年9月常州外國語學校九上數學期初考試第7題進行了打磨。

（常州外國語學校九上數學期初考試第7題）

如圖，ΔOAC和ΔBAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函數y=在第一象限的圖像過點B，則ΔOAC與ΔBAD的面積之差SΔOAC-SΔBAD為_________

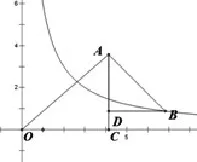
分析：

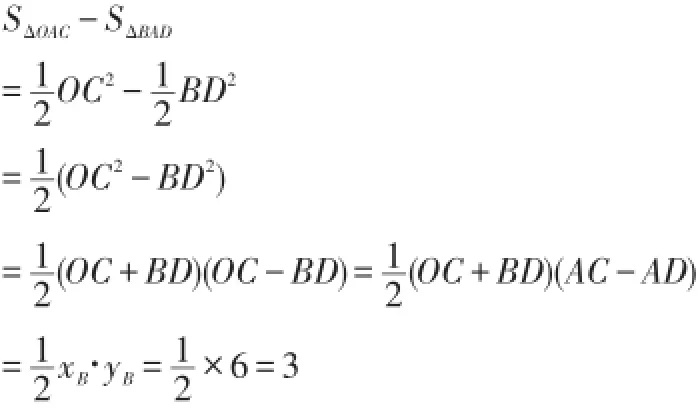
變式（語言互譯）

如圖，ΔOAC和ΔBAD是等腰直角三角形，∠ACO=∠ADB=90°，反比例函數y=在第一象限的圖像過點B，則OC·CD+AD·DC為_____；OA2-AB2=_______

［1］劉蔣巍.“加強條件”與“弱化條件”——淺談變式教學的兩種方法［J］.考試周刊，2016（65）