運動控制在變槳控制系統中的應用

繆新磊，　秦棟平

福氏新能源技術(上海)有限公司　上海　201203

?

運動控制在變槳控制系統中的應用

繆新磊，秦棟平

福氏新能源技術(上海)有限公司上海201203

風力發電變槳控制系統本質上是一個運動控制系統,運動控制系統的跟隨誤差、定位時間和定位誤差會影響變槳的性能,從而影響發電機的輸出功率。從運動控制角度出發，分析了單軸變槳系統的數學模型，在原有PID控制器基礎上引入速度前饋和加速度前饋，并用MATLAB軟件進行了仿真驗證。在某風機的實際應用中，仿真代碼導入控制器，結果顯示引入的前饋控制器可有效提高發電機輸出功率的平穩性。

運動控制; 前饋; 控制器; 發電

作為自動控制的重要分支，運動控制技術[1]在很多領域大顯身手，應用及其廣泛，例如軍事和宇航方面的雷達天線、火炮瞄準、慣性導航、衛星姿態，以及飛船光電池板對太陽跟蹤的控制等。工業方面的各種加工中心、注塑機、數控機床、工業機器人、風力發電機等也要用到運動控制。

運動控制就是通過機械傳動裝置對運動部件的位置、速度進行實時控制管理,使運動部件按照預期的軌跡和規定的運動參數(如速度、加速度參數等)完成相應的動作。運動控制系統由于能夠實現對運動軌跡、運行速度、定位精度及重復定位精度的精確控制，所以在以上所述各類控制工程中有著廣泛應用。

一個狹義的運動控制系統包括運動控制器、伺服驅動器、交流伺服電機、反饋裝置、機械傳動機構和負載等[2]。運動控制系統快速精確的響應可以極大地提高驅動系統的性能，但與此同時，位置偏差及速度波動存在于很多機電系統的應用中，如風力發電變槳控制系統。

出于簡化理論分析的需要，風力發電變槳控制系統可以用兩慣性模型進行描述。在經典的兩慣性控制問題中，通常假設只有驅動側的速度反饋信號，而驅動力矩、負載側的速度反饋和擾動力矩均不可測量，因此要求設計的控制器在僅使用驅動側速度反饋的前提下，能夠對負載側進行有效地速度控制和位置控制。在風力發電系統中，如果能在變槳過程中降低位置偏差和速度波動，將會有效減小發電機功率輸出的波動，并減小對電網的沖擊。

該經典控制問題有一些解決方案，如基于極點配置的PI/PID控制器、基于狀態反饋的兩自由度控制結構等[3]。此外，眾所周知，低階的PID控制器及其變形在運動控制系統中具有壓倒性的普及率，繼續改善包括PID控制器在內的低階控制器設計無論在理論上還是在實際中都有著重要的意義。

筆者建立了電機與負載的模型，在原有PID控制器基礎上加入了速度前饋和加速度前饋[4]，有效降低了機械振動和跟隨誤差，使風力發電系統能夠平穩地輸出功率。

1　變槳控制系統的運動控制模型

變槳系統中每個槳葉采用一個單獨的帶旋變反饋的伺服電機[5]，驅動機械傳動機構進行調節。具體而言,伺服電機由減速箱通過主動齒輪與槳葉輪轂內齒圈相連，帶動槳葉進行轉動，實現槳葉的槳距角控制。在輪轂內齒圈的邊上再安裝一個SSI編碼器，直接檢測內圈轉動的角度，即槳葉槳距角變化，但這一參數不用作運算，即系統實際上是半閉環控制。

1.1單軸運動控制模型

變槳伺服控制系統可以簡單理解為三個單獨軸的點位運動，其核心控制思想為單軸的運動控制。單軸的兩慣性電機與負載模型如圖1所示。

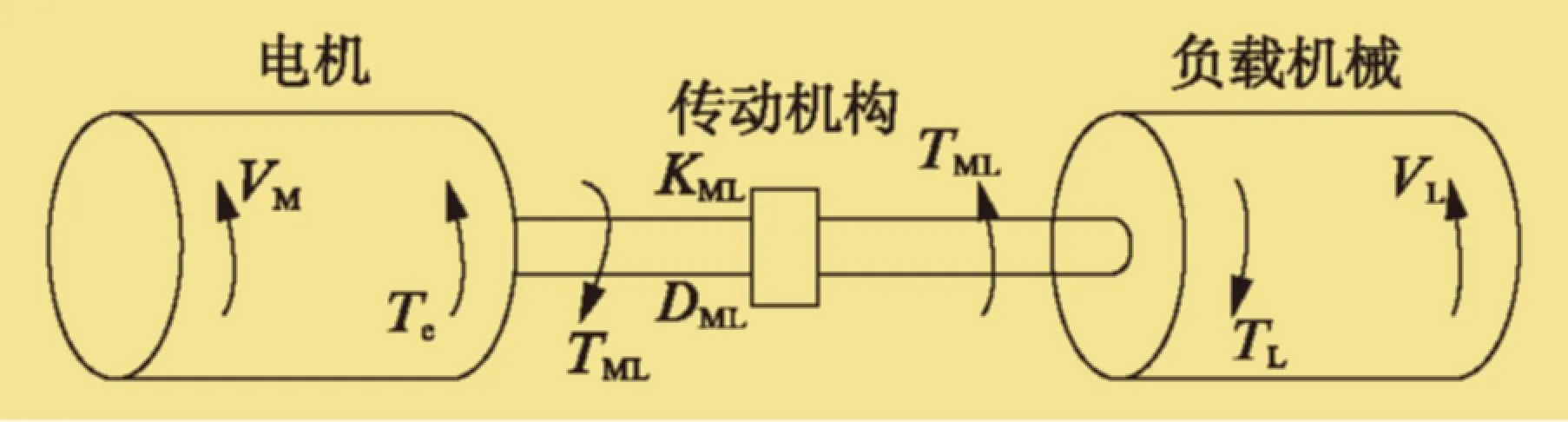
圖1　電機與負載模型

圖中KML為傳動機構的彈性系數，DML為傳動機構的黏性摩擦因數，VM為電機速度，VL為負載速度，TML為力矩。根據圖1可以得出下式：

(1)

式中：1/s為積分環節。

(2)

(3)

式中：ωr為共振頻率；ωα為反共振頻率；ζr為阻尼比；J為轉動慣量；GTM(s)和GTL(s)為傳遞函數。

出于一般性討論的目的，用s*=s/ωα替換s[6]，方程可以正規化為：

(4)

式(4)中q可以定義為慣性比，即驅動側慣性Jm與兩慣性系統全體慣性(Jm+Jl)的比值：

(5)

如圖2所示，隨著慣性比q的增大，共振頻率和反共振頻率會趨于接近，即傾向于零極點抵消。而零極點抵消會導致系統魯棒性的降低，同時共振頻率降低會導致控制系統需要提供更強的阻尼，從而會犧牲系統的穩定裕度和帶寬，所以兩慣性系統控制器的設計難度直接由慣性比q的大小決定。

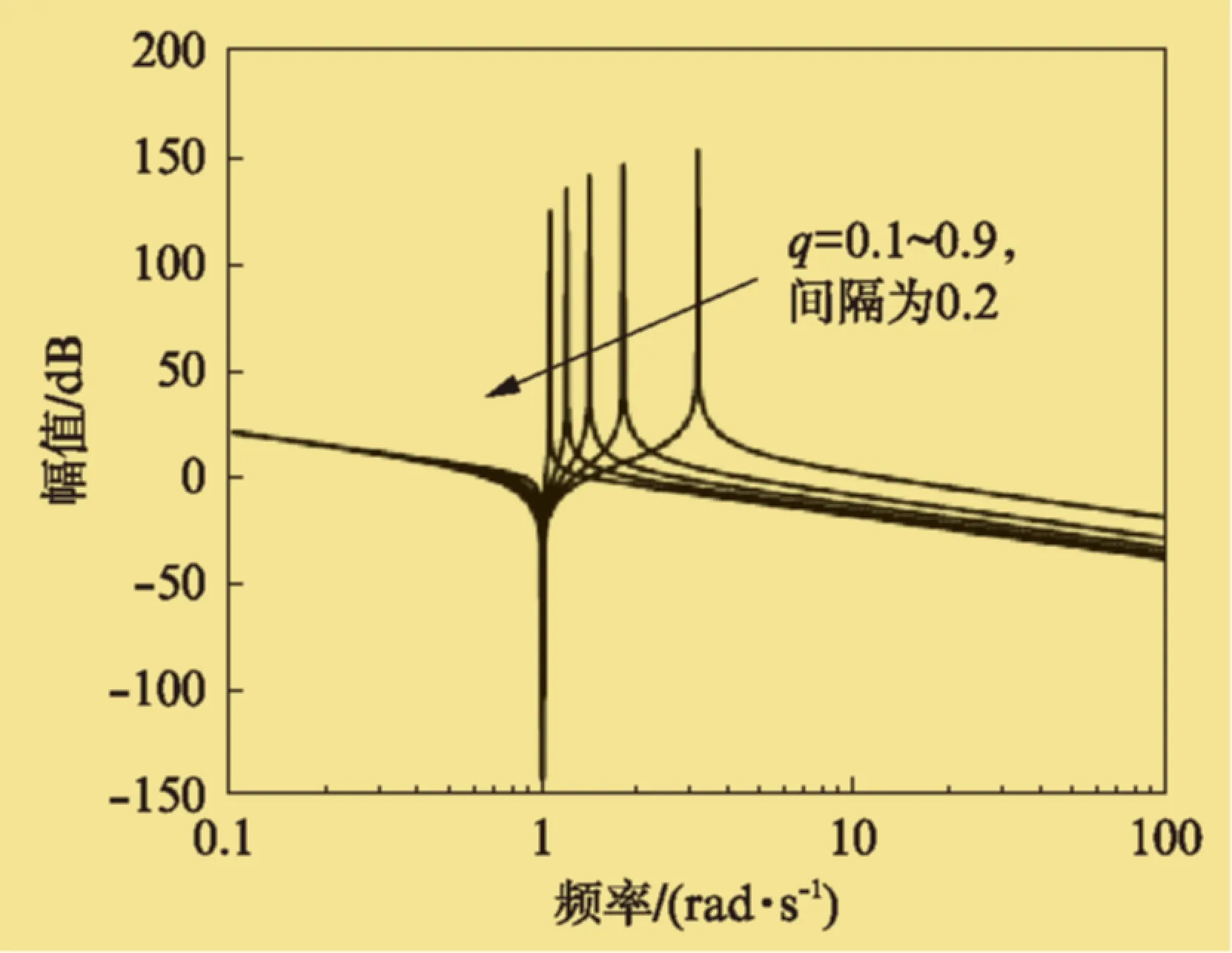
圖2　正規化兩慣性模型的伯德幅值圖

1.2變槳系統數學模型

風力變槳系統[7]由變槳控制器、變槳電機、傳動系統、風機槳葉構成。根據變槳電機、傳動系統和風機槳葉的力矩平衡關系，得到變槳系統數學模型：

(6)

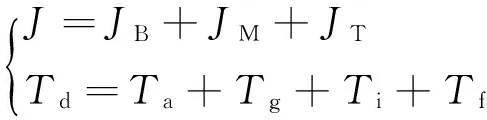
式中：J為折算到電機軸的變槳系統轉動慣量，包括變槳電機的轉動慣量JM、折算后傳動系統的轉動慣量JT、折算后風機槳葉的轉動慣量JB；ω為變槳電機轉速；b為與變槳轉速有關的阻尼系數；Td為折算至電機軸的變槳系統擾動力矩,包括折算后的氣動負載Ta、重力負載Tg、慣性負載Ti和摩擦負載Tf擾動力矩；TM為變槳電機的輸出力矩。

對于運動控制而言，慣量匹配是一項非常重要的特性需求，而對于驅動器而言，良好的慣量匹配才能產生良好的動態性能。在理想的剛性連接情況下，僅需計算出所需扭矩，即可驅動系統，并使其處于高動態特性運轉狀態。然而，由于機械系統(例如減速機、皮帶、聯軸器等)的連接具有彈性變形，無法實現真正意義上的高動態控制特性，這就帶來了慣量匹配問題[8]。在驅動器對負載的控制過程中，電流環的計算周期非常短，在慣量匹配值較大的情況下，系統需要給出一個非常大的偏差才能在PID調節中實現輸出，當然，此時這一輸出的扭矩會產生較大的振動。

2　前饋的引入

風力機主控系統結合當前風速、發電機功率等狀態數據,下發槳葉節距角位置指令。變槳系統實時響應主控指令，驅動槳葉達到指定角度位置。為避免風速變化引起的大型風力發電機輸出功率波動，系統在超過或低于額定風速下運轉時，主動調節槳葉的節距角，改變傳送到傳動軸的轉矩，從而使運行滿足恒轉矩和恒功率[9]。

在風力發電系統中，伺服系統的定位時間、定位誤差及跟隨誤差是需要控制的幾個參數。變槳系統需要實時響應主控發來的位置指令，在最短的時間內運動到指令位置，以滿足功率輸出的需要。跟隨誤差與運動速度相關，一般而言，速度越大，跟隨誤差越大，如果在位置環加入速度前饋，可以有效減小高速運動中的誤差，降低對電網的沖擊。速度前饋一般是實際反饋速度相乘一個比例值，并將所得加到由位置環PID運算出的速度指令上。

速度前饋的引入有效減小了位置跟隨誤差，但加減速階段的位置跟隨有些偏大。此時在速度前饋的基礎上，引入加速度前饋，這一附加值輸出給驅動器，驅動器在電流環計算中預先給出電流值，即可實現前饋控制。這一附加值是通過系統不斷計算，以微秒級的周期循環并提供給驅動器電流環的。當速度前饋和加速度前饋給出后，根據當前值和機械常數計算出整個運動過程的慣量變化，并計算出力矩輸出的前饋值給電機。這一前饋值與控制器給定值在電流環中的控制輸出進行疊加，使扭矩輸出可以快速實現穩態調整，從而減小扭矩輸出的偏差。

經MATLAB/Simulink仿真工具[10]建模生成的控制器模型可以自動生成技術產生控制器的C代碼，這一代碼無需手工重寫即可載入DEIF AWC400控制器中，應用于實際風電項目。

3　試驗結論

為了獲得足夠的數據，筆者采用DEIF變槳控制系統，將AWC400作為變槳系統的控制器，IMD122A作為變槳伺服電機驅動器，在國內某知名風電公司風力發電機組上作了試驗。

圖3為控制器中引入前饋控制策略后,在發電狀態下從主控數據緩沖區讀取的指令位置與變槳實際位置的偏差，以及功率的對比。圖中橫坐標為時間(s)，左側縱坐標為功率(kW),右側縱坐標為偏差角度(°)。

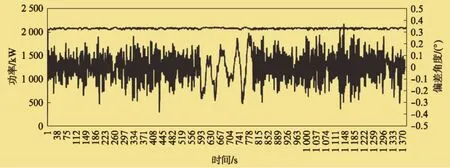
圖3　偏差與功率對比

速度前饋和加速度前饋的引入在很大程度上減小了位置跟隨偏差，速度波動也隨之減小。位置偏差如果能穩定在0.4°內，發電量將很平穩；如果有超過0.4°的區間，發電量將波動異常。

風機如果能保證在風速變化很劇烈的情況下穩定輸出功率，將能有效減小對電網的沖擊。變槳位置跟隨偏差不是影響發電量的唯一因素，但卻不可忽略。變槳運動控制系統采用哪種控制策略將直接決定自身性能，由于變槳系統傳動機構采用減速器及齒輪傳動，可以把變槳系統看成是彈性系統及非線性系統，前饋控制策略并不是專門針對非線性系統設計的，新的控制策略(如多項式控制策略)已在進一步研究之中。

[1] 朱小莉.基于DSP技術的運動控制卡的研究與開發[D].武漢： 華中科技大學，2007.

[2] 汪海波,田煒,魯斌,等.兆瓦級風電機組電動變槳距系統測試平臺設計[J].電力系統自動化,2010,34(24)： 74-77.

[3] 宿敬亞，樊鵬輝，蔡開元.四旋翼飛行器的非線性PID姿態控制[J].北京航空航天大學學報，2011，37(9)： 1054-1058.

[4] 楊輝，吳欽章，范永坤，等.加速度前饋在高精度伺服跟蹤系統中的應用研究[J].光電技術應用，2007，22(6)： 48-51.

[5] 陳遠，樊亞東，江政，等.小型永磁同步電機溫度場分析中幾個關鍵問題的解決方法[J].上海電氣技術，2009，2(3)： 50-52.

[6] MA C B, CAO J Y, QIAO Y. Polynomial-method-based Design of Low-order Controllers for Tow-mass Systems[J]. IEEE Transactions on Industrial Electronics, 2013,60(3): 969-978.

[7] 禹華軍.風力發電機組中的振動監測與分析[J].裝備機械，2011(3)： 52-56.

[8] 宋華振.淺述貝加萊機器人控制中的慣量前饋控制技術[J].伺服控制,2011(8)： 91-92.

[9] 葉成城.兆瓦級風電機組電動變槳距控制系統的研究與實現[D].上海： 上海交通大學,2013.

[10] 陳永剛，劉大勇，閻秋生.基于PMAC的直線電機高定位增益前饋PID控制算法研究[J].機械制造，2013，51(12)： 35-37.

Wind turbine pitch control system is essentially a motion control system, the following error, positioning time and positioning errors of the motion control system can affect the performance of the pitch, thereby, it may affect the output power of the generator. From the perspective of the motion control, the mathematical model of the uniaxial pitch system was analyzed and the velocity feedforward and acceleration feedforward were introduced on the base of the original PID controller. It was demonstrated via the simulation by MATLAB software. In practical blower fan applications, the simulation code was led into the controller. The results show that the lead-in feedforward controller could effectively improve the smoothness of the generated output power.

Motion Control; Feedforward; Controller; Power Generation

2015年10月

繆新磊(1987—)，男，碩士，助理工程師，主要從事變槳控制系統工作，

E-mail： smi@deif.cn

TM614

B

1674-540X(2016)02-049-04