含裂紋懸臂梁的振動特性分析

孔　成，續秀忠

（上海海事大學 物流工程學院，上海 201306）

含裂紋懸臂梁的振動特性分析

孔成，續秀忠

（上海海事大學 物流工程學院，上海 201306）

用一無質量扭轉彈簧來模擬裂紋所在截面，這樣就可以將裂紋梁分為兩段研究。基于兩段完整的梁的振型表達式，推導出了裂紋梁的傳遞矩陣，進而給出懸臂裂紋梁的頻率方程。用Matlab軟件編程求解懸臂裂紋梁的頻率方程，把所得結果與有限元結果進行對比分析，研究裂紋位置和裂紋深度對懸臂裂紋梁固有頻率的影響，驗證了推導方法的合理性。

振動與波；裂紋梁；傳遞矩陣；固有頻率；Ansys；Matlab

在機械工程領域，裂紋的檢測與識別對于保證設備的正常運轉，預防突發事故具有十分重要的意義。在過去幾十年，許多學者對裂紋檢測方法做了廣泛的研究，如超聲檢測法、聲發射法和頻域法［1-2］等，這些方法在裂紋檢測上已取得了很好的效果，但這些方法難以定量分析，識別準確度不高［3］。基于振動特性的損傷檢測近年來越來越受到重視［4］，因為結構損傷會對振動系統的動態特性產生影響，使得振動系統的有關參數發生改變，如固有頻率和振型將發生相應的變化，這具有重要的工程意義。

過去幾十年，許多學者對裂紋梁固有頻率的計算做了廣泛的研究，并獲得了許多計算裂紋梁固有頻率的方法［5-6］。本文對裂紋所在截面用一無質量扭轉彈簧來代替，這樣就將含裂紋的懸臂梁分為兩段完整的梁，基于梁的振型表達式，推導出了裂紋懸臂梁的傳遞矩陣，結合具體的邊界條件給出了懸臂裂紋梁的頻率方程，用Matlab編程方法求解了懸臂裂紋梁的頻率方程。并就裂紋懸臂梁進行了數值模擬，研究了裂紋位置和裂紋深度對固有頻率的影響。

1　裂紋梁傳遞矩陣

懸臂梁的自由振動方程［7-8］

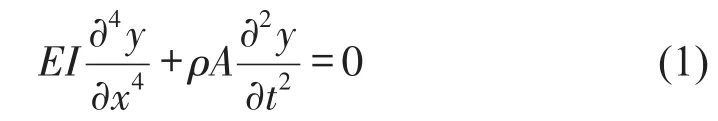
式中EI——梁的彎曲剛度；ρ——梁的密度。由于梁的振型與時間無關，所以設代入式（1），得

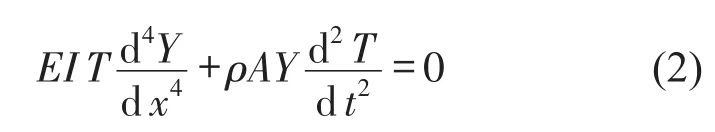
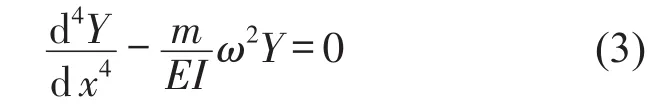
方程（3）的解具有如下形式

對于懸臂梁的裂紋截面，我們可以將其看成是由兩根梁通過一扭轉彈簧連接［9］，如圖1所示。

圖1　裂紋梁模型及其等效模型

這樣懸臂裂紋梁被分成了兩段，其振型可寫為

式中C1～C8——常數；xc——裂紋所在截面的橫坐標。

由Dimarogonas和Paipeties理論［10］，在裂紋處其撓度、剪力和彎矩是連續的，而轉角不連續。轉角滿足的條件為

式中ξ=a/H——相對裂紋深度；f（ξ）——柔度函數，可由應變能密度函數求得

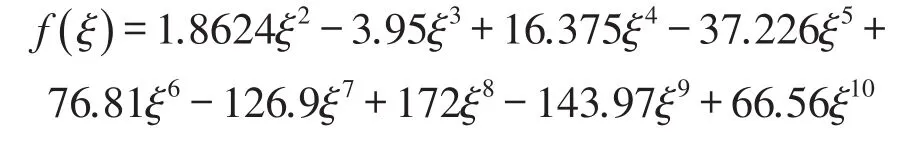
裂紋兩邊的撓度、轉角、彎矩以及剪力滿足關系

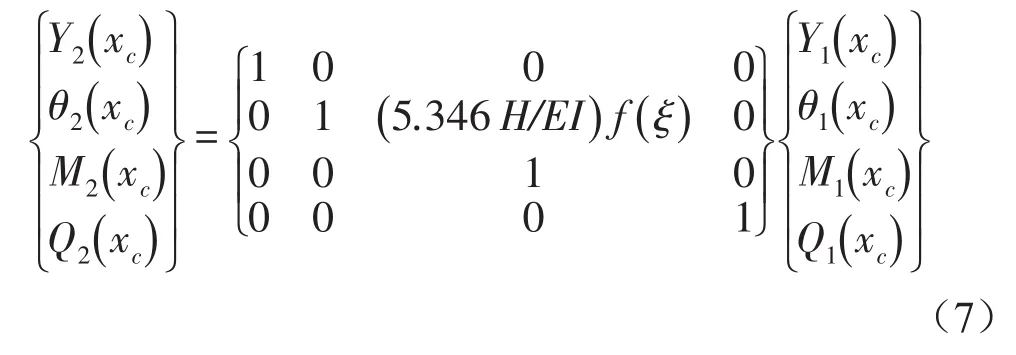
根據完整梁振動問題的傳遞矩陣解法知

式（10）就是裂紋梁的傳遞矩陣。

把傳遞矩陣寫成如下形式

由懸臂梁的邊界條件

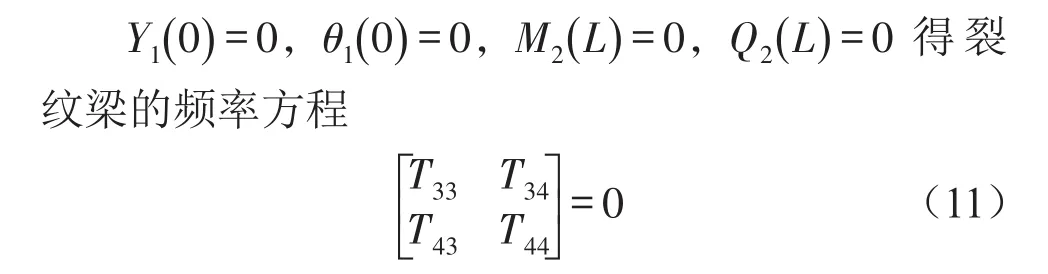
2　算例分析

2.1傳遞矩陣方法

應用前述推導的傳遞矩陣法，結合懸臂梁的邊界條件得到了方程（11），運用Matlab軟件對方程（11）進行求解，從而對懸臂裂紋梁進行數值計算，計算中使用的幾何參數和材料常數為長L為0.3 m，截面尺寸寬b為0.02 m，高h為0.02 m，材料的彈性模量200 GPa，泊松比為0.3，質量密度為7.85×103kg/m3。

令Q=T33×T44-T43×T34，編制Matlab程序，求解這個函數會得到一條以頻率作為自變量的函數曲線，函數曲線如圖2所示。

函數的零點就是方程（11）的根，也就是我們所需要的固有頻率值。

裂紋深度為定量，裂紋深度a=0.002 m時，通過改變裂紋的位置，來計算裂紋在不同位置時懸臂梁的1階固有頻率。表1列出了不同裂紋位置下的懸臂梁1階固有頻率：

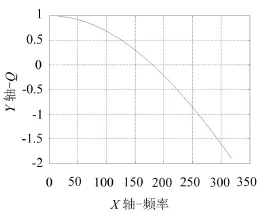
圖2　關于頻率的函數曲線

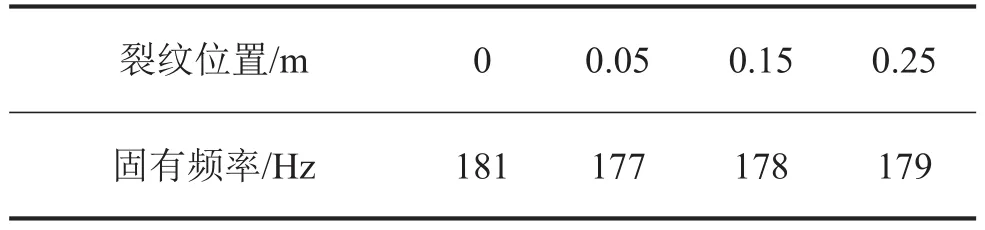
表1　不同裂紋位置時的1階固有頻率（裂紋深度0.002 m）

裂紋位置為定量，裂紋位置x=0.15 m時，通過改變裂紋的深度，來計算裂紋在不同深度時懸臂梁的1階固有頻率。表2列出了不同裂紋深度下的懸臂梁1階固有頻率。

表2　不同裂紋深度時的1階固有頻率（裂紋位置0.15 m）

從傳遞矩陣法的計算結果來看，當裂紋深度為定值時，裂紋位置的改變也會引起固有頻率的改變。隨著裂紋位置遠離梁的固定端，其固有頻率在增大，與正常懸臂梁固有頻率相比，其固有頻率的減小量在縮小，如表1所示。當裂紋位置為定值時，裂紋深度的改變也引起了固有頻率的改變。隨著裂紋深度的增大，其固有頻率在不斷減小，如表2所示。

2.2有限元方法

對懸臂梁進行有限元分析，有限元模型和單元劃分，如圖3所示。模型的幾何參數和材料常數與上文中使用的參數保持一致。分析中使用Shell單元，就懸臂梁進行計算。計算結果列于表3和表4。如表3所示，在裂紋深度為定量時，不同裂紋位置時懸臂梁的1階固有頻率；如表4所示，在裂紋位置為定量時，不同裂紋深度時懸臂梁的1階固有頻率。

圖3　裂紋梁有限元模型

表3　不同裂紋位置時的1階固有頻率（裂紋深度0.002 m）

表4　不同裂紋深度時的1階固有頻率（裂紋位置0.15 m）

從圖4和圖5可以看出，本文的計算結果與有限元計算結果基本吻合，計算各組數據之間的誤差，其誤差均在1%左右，誤差較小，說明準確度較高，驗證了本文推導方法的合理性。

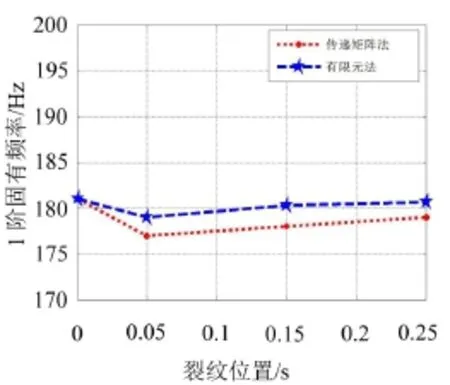
圖4　不同裂紋位置時的1階固有頻率

圖5　不同裂紋深度時的1階固有頻率

3　結語

本文推導了含裂紋的懸臂梁的傳遞矩陣，并給出了懸臂裂紋梁的頻率方程。通過用Matlab編程的方法求解懸臂裂紋梁的頻率方程，得到了含裂紋梁的固有頻率。針對同一算例應用有限元方法，同樣得到了含裂紋梁的固有頻率。將兩種方法的結果進行對比，驗證了本文所推導理論方法的合理性，同時也得到了如下結論：

（1）當裂紋深度為定值時，隨著裂紋位置遠離梁的固定端，其固有頻率在增大，與正常懸臂梁固有頻率相比，其固有頻率的減小量在縮小。

（2）當裂紋位置為定值時，隨著裂紋深度的增大，其固有頻率在不斷減小。

［1］王金福，李富才.機械故障診斷的信號處理方法:頻域分析［J］.噪聲與振動控制，2013，33（1）：173-180.

［2］孟范孔，邱志成.梁損傷小波包分析和神經網絡識別［J］.噪聲與振動控制，2013，33（1）：197-200+207.

［3］張敬芬，趙德有.工程結構裂紋損傷振動診斷的發展和展望［J］.振動與沖擊，2002，21（4）：22-26.

［4］李兵，陳雪峰.基于小波有限元的懸臂梁裂紋識別［J］.振動工程學報，2004，17（2）：159-164.

［5］陳夢成，湯任基.一種裂紋梁振動響應分析的近似方法［J］.應用數學和力學，1997，18（3）：204-209.

［6］李學平，余志武.含多處裂紋梁的振動分析［J］.應用力學學報，2007，24（1）：66-69.

［7］張佐輝，李學平.存在裂紋梁的動力分析［J］.長沙鐵道學院學報，2003，21（2）：105-108.

［8］茍兵旺，劉永壽，等.軸向壓力影響下裂紋梁振動特性分析［J］.機械設計與制造，2009（12）：211-213.

［9］RIZOS P F，ASPRAGATHOS N，DIMAROGONAS A D. Identification of crack location and magnitude in a cantilever beam［J］.Journal of Sound and Vibration，1999，138:381-388.

［10］DIMARONAS A D PAIPETIES S A.Analytical methods in rotor dynamics［M］.Elsevier applied science，London，1983.

Analysis of Vibration Characteristics of Cracked Cantilever Beams

KONGCheng，XU Xiu-zhong
（College of Logistics Engineering，Shanghai Maritime University，Shanghai 201306，China）

Simulating the cracked section by a massless torsion spring，the cracked cantilever beam can be divided into two sub-beams.Based on the vibration modes of the two sub-beams，the transfer matrix of the cracked cantilever beam is obtained.Frequency equation of the cantilever beam is given and solved by Matlab.The results are compared with those of finite element method.The effect of crack location and crack depth on the natural frequency of the cantilever beam is analyzed.The rationality of this method is verified.

vibration and wave；cracked beams；transfer matrix；natural frequency；Ansys；Matlab

TH113；O322

ADOI編碼：10.3969/j.issn.1006-1335.2016.05.007

1006-1355（2016）05-0031-03+50

2016-05-06

上海海事大學研究生創新基金資助項目（2015ycx036）

孔成（1989-），男，江蘇省泰興市人，碩士生，主要研究方向為機械動態性能監測。E-mail:kong6616@163.com

續秀忠，男，副教授，碩士生導師。E-mail:896534896@qq.com