共振速度下軌道交通槽形梁結構瞬態噪聲分析

劉林芽，曾　峰，姚忠達，許代言

（1.華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，南昌 330013；2.臺灣淡江大學 土木工程學系，臺灣 新北 25137）

共振速度下軌道交通槽形梁結構瞬態噪聲分析

劉林芽1，曾峰1，姚忠達2，許代言1

（1.華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，南昌 330013；2.臺灣淡江大學 土木工程學系，臺灣 新北 25137）

為了進一步研究不同列車速度下的橋梁結構噪聲問題，基于有限元-瞬態邊界元理論，針對軌道交通30 m簡支槽形梁，分析在共振、消振速度下橋梁的振動響應及結構聲輻射特性。首先，建立槽形梁振動輻射瞬態噪聲的有限元/邊界元模型；然后，對簡支梁在移動列車荷載下誘發的振動進行分析，得到列車荷載通過橋梁時的共振和消振速度；最終，結合聲輻射理論，采用瞬態邊界元法研究分析不同列車速度引起的橋梁瞬態噪聲聲場特性。研究結果表明:列車速度的變化引起橋梁結構的位移幅值出現波動性變化；橋梁結構的振動加速度幅值隨著速度的增大而不斷增大；橋梁結構輻射噪聲的變化趨勢與結構的振動加速度變化趨勢有一定的相關性；當列車以共振速度通過簡支橋梁時，結構動力響應值及輻射噪聲值有放大趨勢，在附近出現峰值；列車共振速度對橋梁結構的遠聲場瞬態噪聲影響效果較為顯著；應有針對性地控制列車速度以改善橋梁結構噪聲。

振動與波；槽形梁；移動荷載；共振；消振；瞬態聲輻射特性

隨著經濟的飛速發展，城市化進程的加快，城市交通擁堵問題日益嚴峻，而世界各國普遍認識到，緩解城市擁堵的根本出路在于發展以城市軌道交通為主的公共交通系統。高架橋梁因其造價低、美觀等優勢，在城市軌道交通全線中所占的比重也越來越大。伴隨著高架橋承受的交通流量日益增多，列車荷載作用下橋梁的振動與噪聲問題也逐漸受到人們的關注。其中列車過橋時引起的共振問題一直是國內外相關學者關注的重點，人們對這個問題進行了較為系統的研究，取得了很多成果。

Yang等采用解析法研究了移動荷載作用下兩端彈性支承簡支梁的共振、消振現象［1-2］。Yau等采用解析法、數值法相結合研究了移動荷載作用下多跨連續梁的振動響應［3］。Xia等分別從理論分析、數值模擬及試驗分析出發，研究了列車荷載作用下簡支梁的振動響應理論解，獲得簡支梁發生共振及消振的車速計算公式［4，6］。黃方林等通過建立時變的移動荷載-簡支梁系統，研究了橋梁結構的豎向振動［7］。以上研究，對共振速度引起的結構輻射噪聲問題較少涉及。

吳定俊等研究指出橋梁結構輻射噪聲與列車車速有一定的關系，但目前還無權威定論［8］。Moritoh等通過對高速鐵路高架線的測試研究發現：距離高架橋線路中心25 m時橋梁結構噪聲與列車速度有一定的相關性［9］。Au等對移動荷載作用下的正交各向異性薄板的振動聲輻射問題進行分析，分析表明，移動荷載的速度越大，產生的聲壓越大［10］，而劉加華研究指出結構的低頻噪聲隨列車速度的增大無顯著變化［11］，賀建良等研究發現，車速越低，橋面振動輻射噪聲對總噪聲的貢獻越大［12］。因此，列車速度對橋梁結構噪聲的影響，尤其列車共振速度下誘發的高架橋梁結構低頻噪聲問題還須進一步研究。

本文以某擬建軌道交通槽形梁為研究對象，針對簡支梁在移動列車荷載下誘發的振動進行分析，得到列車荷載通過橋梁時的共振和消振速度，基于有限元-瞬態邊界元理論，建立軌道-槽形梁有限元模型和聲學邊界元模型，采用移動荷載模型，并以該模型激勵下得到的槽形梁結構振動響應作為聲源，采用瞬態邊界元法分析橋梁振動產生的聲場，計算不同列車速度下槽形梁結構瞬態聲輻射情況，為控制共振速度下的車橋振動誘發的結構噪聲控制提供了可行性方案。

1　分析模型

1.1移動列車荷載模型

為了更好地反映列車通過橋梁時，因荷載周期性加載引起的橋梁振動互相疊加出現的共振現象，及其對橋梁結構輻射噪聲的影響，本文采用移動列車荷載模型，高傳偉等研究表明采用移動列車荷載模型分析城市軌道交通橋梁的動力響應，分析精度是足夠的［13］。

移動列車荷載模型可以分析車長、軸距、軸重和車速等參數對橋梁輻射噪聲的影響及規律。結合國內（上海、廣州、南京、重慶等）已使用的列車車輛資料，城市軌道交通車輛豎向荷載可以簡化為如圖1所示的荷載列。

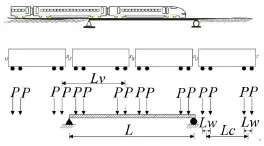
圖1　移動列車軸重荷載過橋分析模型

移動列車荷載將每節列車的軸重荷載用集中力P表示，并參照輪對實際位置布置，荷載之間存在以下幾種間距排列：Lv為車輛全長；Lc為轉向架中心距；Lw為輪對的軸距。

1.2軌道交通槽形梁有限元模型

基于有限元理論，建立軌道交通槽形梁模型，在分析模型中，所有材料均處于線彈性階段，將鋼軌視為Euler梁，用梁單元模擬；槽形梁梁體、軌道板、CA砂漿層均用實體單元模擬，為避免病態網格的出現，采用體掃掠法劃分將其劃分為大小合適的六面體單元；連接鋼軌與軌道板的扣件系統采用間距為0.625 m的離散彈簧阻尼單元模擬，主要材料參數如表1。

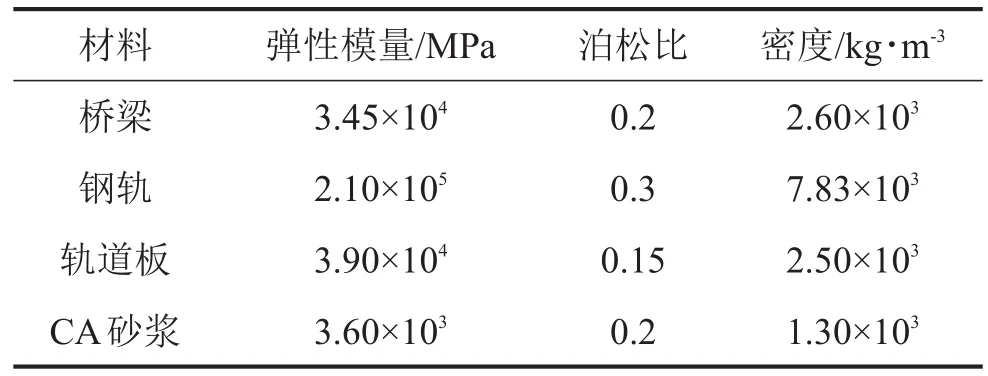
表1　槽形梁模型主要材料參數表

槽形梁的截面形式采用某擬建軌道交通選用的簡支槽形梁，梁體腹板一側為圓弧結構、另一側采用折腹線式直線的不對稱結構，有限元模型如圖2所示。各項參數經過多次調試，能滿足GB50157-2013地鐵設計規范的要求。

圖2　軌道交通槽形梁有限元模型

1.3軌道交通槽形梁邊界元模型

瞬態邊界元法就是基于有限元法求解的橋梁瞬態動力響應結構通過插值的方法分配到橋梁結構聲學邊界元網格上作為邊界條件，然后求解出槽形梁的瞬態聲輻射特性。

槽形梁的表面為封閉的邊界表面，通過對其離散，可以得到邊界元求解方程

其中A、B為系數矩陣；p（ra）、vn（ra）分別是封閉邊界表面Ωa的聲壓和方向速度。槽形梁表面外部無限域V內任意一點的聲壓可以通過Helmholtz積分方程求得。

瞬態邊界元法用于計算橋梁結構振動聲輻射問題時，不僅能夠反映聲壓在時間域的分布，并且能夠合理反映列車荷載作用下橋梁輻射低頻噪聲情況，同時避免了采用模態疊加法時出現的模態截斷誤差，與穩態邊界元相比，避免了對邊界條件進行穩態簡化，計算精度更有保障。

本文基于瞬態邊界元理論建立槽形梁結構聲輻射邊界元模型，如圖3所示。

圖3　軌道交通槽形梁邊界元模型

在進行瞬態邊界元分析計算時，邊界元網格必須是三角形網格，故使用自由網格劃分。

2　移動列車荷載下的共振分析

北京交通大學夏禾教授等對簡支梁橋的車橋豎向共振問題進行了研究，他采用移動的荷載列來模擬車輛模型，通過振動響應分析得出任意模態下橋梁的共振及兩類消振的解析表達式［14］

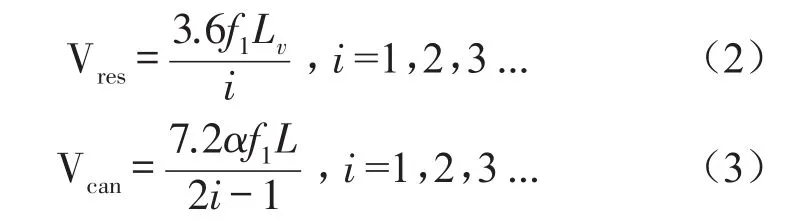
式中Vres為共振列車速度，Vcan為消振列車速度。f1為橋梁1階豎向自振頻率，本文中f1=3.165 7；Lv=20 m，為車輛全長；L為橋梁全長，本文L=30 m；α為無量綱參數，α=1表示第一類消振效應。

根據圖1可以計算出不同橋梁跨徑的1階豎向振動，然后代入式（2）、式（3）可以計算出車輛和橋梁的豎向共振速度和消振速度，計算結果見表2，并將大于120 km/h，小于40 km/h的速度舍棄。

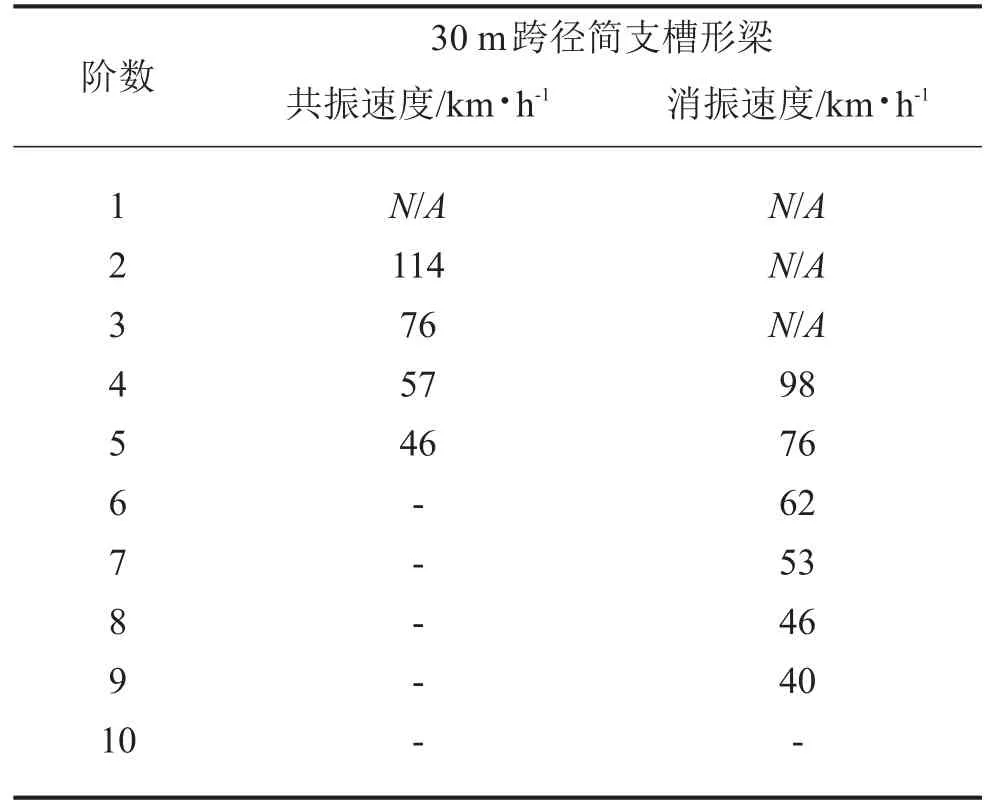
表2　簡支槽形梁1階振型的共振與消振車速

3　計算結果與分析

3.1軌道交通槽形梁的動力響應計算與分析

重點研究共振速度下橋梁結構的振動響應，不考慮橋上車輛的振動情況，因此車輛與橋梁的耦合作用不再考慮。車輛模型簡化為勻速運動的集中荷載列。

結構振動輻射噪聲主要由橋梁的法向振動響應產生，由于移動荷載的周期性排列，會對橋梁結構產生周期性作用，這對橋梁結構的振動響應具有重要影響。計算中保持其它參數不變，對列車速度在40 km/h～120 km/h范圍內的軌道交通槽形梁結構動力響應進行分析。選取橋梁跨中截面底板輸出不同車速下橋梁結構的振動響應計算結果，如圖4、圖5所示。

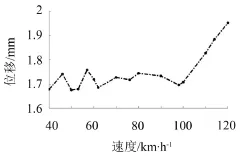
圖4　軌道交通槽形梁底板跨中最大位移

圖4和圖5分別給出了不同列車時速下橋梁跨中截面底板的最大位移值和最大加速度值的變化情況。從圖4中可以看出：隨著速度的增加，橋梁跨中豎向最大位移值出現波動性變化。從圖5中可以看出：隨著速度的增加，橋梁各跨的豎向振動加速度隨著車速的增加幾乎呈線性增加。在共振速度處，加速度值有放大趨勢，在附近出現峰值。從相關系數R=0.978 7可以看出，列車速度跟橋梁結構振動加速度值兩者之間的相關性較為顯著。

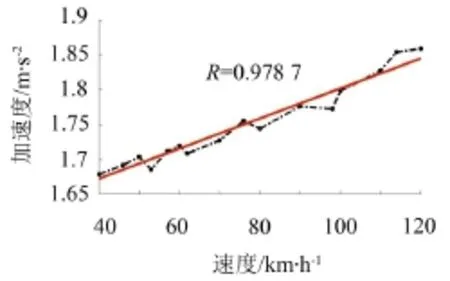
圖5　軌道交通槽形梁底板跨中最大加速度

表3給出了共振與消振速度下橋梁跨中底板最大加速度值對比分析。據圖5可知，列車速度跟橋梁結構振動加速度值兩者之間的相關性較為顯著，現根據列車速度在40，50，60，...，120 km/h時對應的橋梁跨中底板最大加速度值，進行線性擬合，獲取共振/消振速度下橋梁跨中截面底板最大加速度擬合值，并與數值仿真結果進行差值對比分析。由表3可知，在共振速度114 km/h處，加速度差值有放大趨勢，而在46 km/h，76 km/h處加速度差值很小，這是源于消振速度對其的影響，抑制了結構的共振現象。

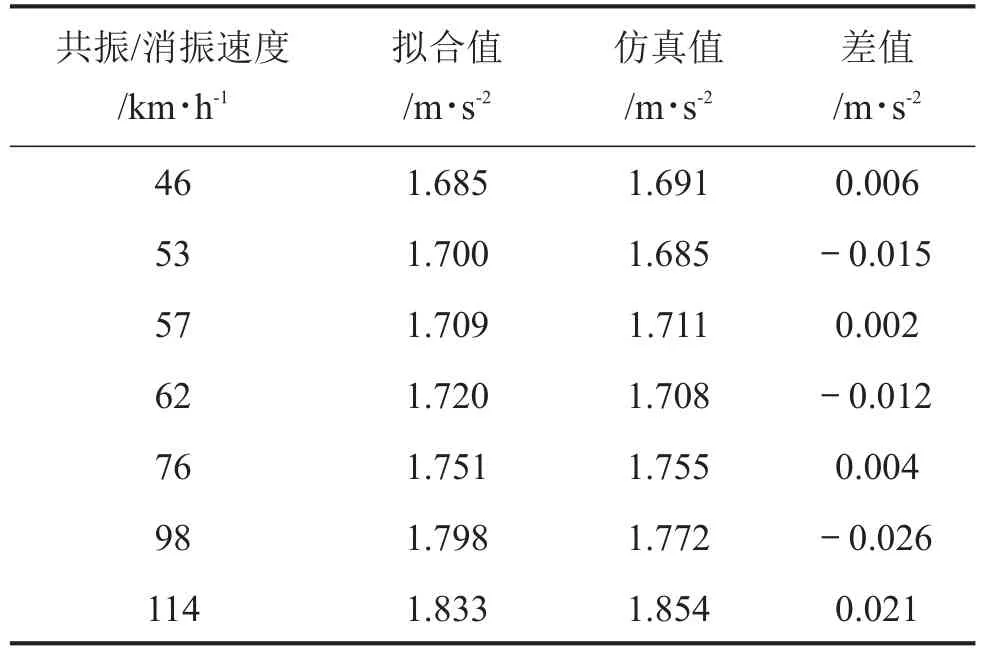
表3　共振/消振車速下橋梁最大加速度值對比分析

3.2軌道交通槽形梁瞬態聲輻射特性分析及場點分布

為了很好地體現橋梁結構振動隨時間變化的聲場特性，采用瞬態邊界元法對軌道交通槽形梁進行結構瞬態聲輻射特性分析，將移動列荷載作為外部激振力加載到軌道-槽形梁有限元模型上，計算得到橋梁瞬態動力響應，作為槽形梁聲學邊界元模型的初始邊界條件，對槽形梁的瞬態輻射噪聲進行分析計算。

在時域內計算槽形梁結構聲學響應時，由于只研究槽形梁梁體結構噪聲，因此忽略了橋墩的影響，擬建橋梁輻射聲場場點如圖6所示。

圖6　場點分布圖

3.3軌道交通槽形梁瞬態聲輻射計算與分析

采用有限元軟件，建立軌道-槽形梁有限元模型，并將采用基于移動列車荷載模型加載激振力到所建立的有限元模型上，進行槽形梁的瞬態動力響應分析，以槽形梁動力響應結果作為邊界條件，預測分析不同列車速度下槽形梁梁體瞬態噪聲情況。同時，為了更好地反映共振速度下軌道交通槽形梁結構噪聲的空間輻射情況，分別選取1號場點作為近聲場評價點，3號場點作為遠聲場的評價點。

圖7、圖8分別給出了不同列車時速下軌道交通槽形梁輻射聲場1號場點和3號場點的最大聲壓級。據圖可知：隨著列車速度的增加，橋梁結構輻射噪聲最大聲壓級越大，列車速度越高，對高架橋梁結構噪聲的影響越明顯。在共振速度處，最大聲壓級值有放大趨勢，在附近出現峰值。從相關系數R可以看出，列車速度跟橋梁結構振動輻射聲壓級值兩者相關性較為顯著。

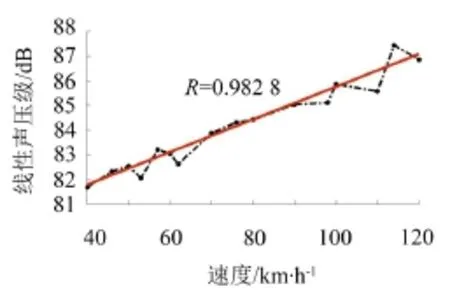
圖7　軌道交通槽形梁輻射聲場1號場點最大聲壓級

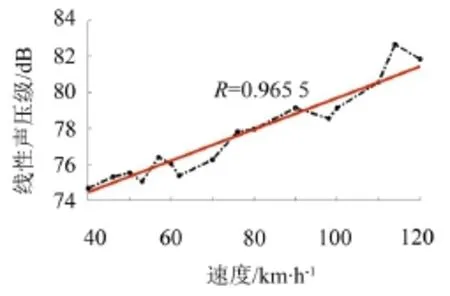
圖8　軌道交通槽形梁輻射聲場3號場點最大聲壓級

表4給出了共振與消振速度下軌道交通槽形梁輻射聲場1號場點和3號場點的最大聲壓級值對比分析。分析圖7、圖8可知，列車速度跟槽形梁輻射聲壓級兩者之間的相關性較為顯著，現依據列車速度在40，50，60，...，120 km/h時對應的橋梁輻射聲場最大聲壓級值，進行線性擬合，獲取共振/消振速度下橋梁1號場點和3號場點的最大聲壓級值擬合值，并于數值仿真結果進行差值對比分析。

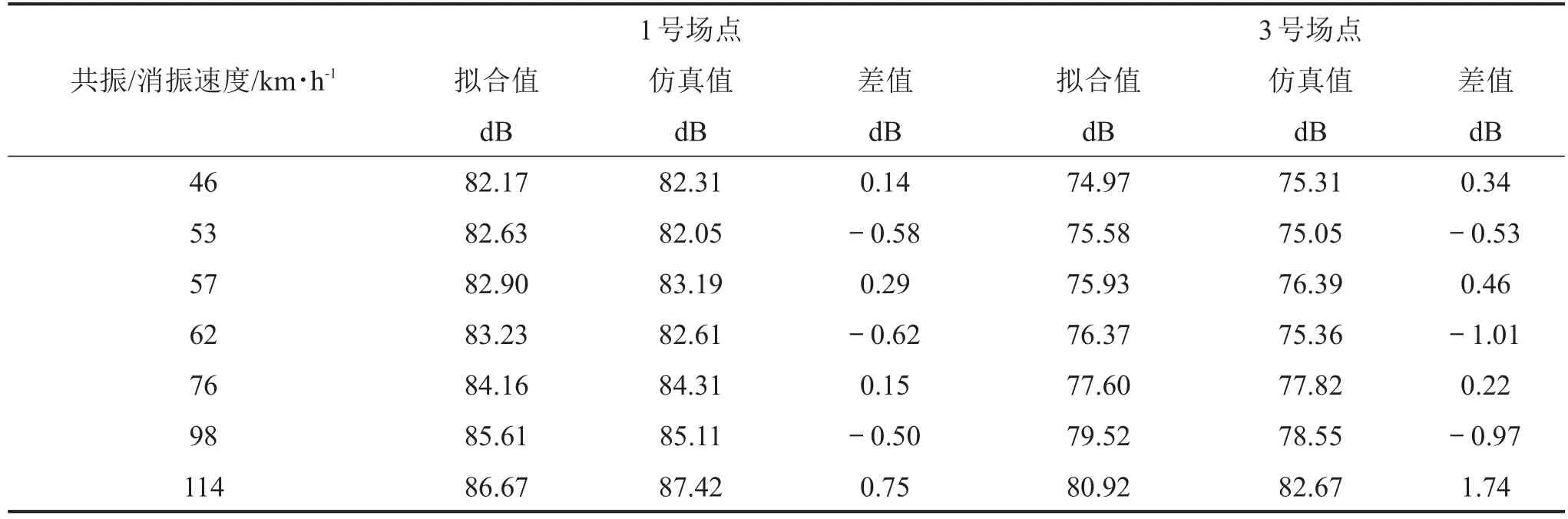
表4　共振/消振車速下場點最大聲壓級值對比分析

由表4可知，在共振速度114 km/h處，最大聲壓級值有放大，而在46 km/h，76 km/h處最大聲壓級差值相對較小，這是源于消振速度對其的影響，抑制了結構的共振現象。同時，對比發現，在共振速度57 km/h、114 km/h等處，3號場點的結構瞬態噪聲最大聲壓級差值與1號場點相比相對較大，可見列車共振速度對橋梁結構的遠聲場瞬態噪聲影響效果較為顯著。

4　結語

本文以某擬建軌道交通高架簡支槽形梁為研究對象，針對簡支梁在移動列車荷載下誘發的振動進行分析，得到列車荷載通過橋梁時的共振和消振速度，結合聲輻射理論，采用瞬態邊界元法研究分析不同列車速度引起的橋梁瞬態噪聲聲場特性，通過數值分析得到以下結論：

（1）隨著列車速度的變化，橋梁結構的位移幅值出現波動性變化，橋梁結構的振動加速度幅值隨著速度的增大而不斷增大。

（2）橋梁結構輻射噪聲的變化趨勢與結構的振動加速度變化趨勢有一定的相關性。

（3）當列車以共振速度通過簡支橋梁時，結構振動以及輻射噪聲有放大趨勢，在附近出現峰值，這為控制列車運行速度避開橋梁共振提供了理論參考。

（4）列車共振速度對橋梁結構的遠聲場瞬態噪聲影響效果較為顯著。

［1］YANG Y B，YAU J D，HSU L C.Vibration of simple beams due to trains moving at high speed［J］.Engineering Structures，1997，19（11）:936-944.

［2］YANG Y B，LIN C L，YAU J D，et al.Mechanism of resonance and cancellation for train-induced vibrations on bridges with elastic bearings［J］.Journal of Sound and Vibration，2004，269（1/2）:345-360.

［3］YAU J D.Resonance of continuous bridges due to high speed trains［J］.Journal of Marine Science and Technology Taiwan，2001，9（1）:14-20.

［4］夏禾，郭薇薇，張楠.車橋系統共振機理和共振條件分析［J］.鐵道學報，2006，28（5）：52-58.

［5］XIA HE，LI H L，GUO W W，et al.Vibration resonance andcancellationofsimplesupportedbridgesunder movingtrainloads［J］.JournalofEngineering Mechanics ASCE，2014，140（5）:04014015.1-04014015. 11.

［6］李慧樂，夏禾，郭薇薇.移動列車荷載作用下簡支梁共振與消振機理研究［J］.工程力學，2013，30（7）：47-54.

［7］陶勝利，黃方林，黃志輝.移動荷載速度對梁橋跨中動力響應影響的分析［J］.噪聲與振動控制，2009，29（2）：27-29.

［8］韓江龍，吳定俊，李奇.城市軌道交通高架結構噪聲研究的進展［J］.城市軌道交通研究，2012，15（3）：109-112+116.

［9］MORITOH Y，ZENDA Y，NAGAKURA K.Noise control of high speed shinkansen［J］.Journal of Sound and Vibration，1996，193（1）:319.

［10］AU F T K，WANG M F.Sound radiation from forced vibration of rectangular orthotropic plates under moving loads［J］.Journal of Sound and Vibration，2005，281（3-5）:1057.

［11］劉加華.從軌道結構降低城市軌道交通高架結構振動與噪聲的研究與應用［D］.上海：同濟大學，2006.

［12］賀建良，萬泉，蔣偉康.高架城市軌道交通的噪聲特性分析［J］.城市軌道交通研究，2007，10（8）：57.

［13］高傳偉，唐雅茹，余華.基于移動荷載過橋的軌道交通橋梁振動研究［J］.中國鐵道科學，2005，26（2）：73-76.

［14］李慧樂，夏禾，郭薇薇.簡支梁在列車荷載下的共振與消振效應［J］.振動工程學報，2014，27（2）：172-179.

Transient NoiseAnalysis of Rail Transit Trough-shaped Beam Structures under Resonant Speeds

LIU Lin-ya1，ZENGFeng1，YAU Zhong-da2，XU Dai-yan1
（1.Engineering Research Center of Railway Environmental Vibration and Noise，Ministry of Education，East China Jiaotong University，Nanchang 330013，China；2.Department of Civil Engineering，Tamkang University，New Taipei 25137）

In order to further study the structural noise of bridges under different train speed condition，the structural noise and sound radiation characteristics of a rail-transit trough-shaped 30 m-span simply-supported beam are analyzed by means of finite element method and transient boundary element theory.First of all，the finite element and boundary element model of the trough-shaped beam is established.Then，vibration of the simply supported beam under moving load excitation is analyzed，and the resonance speed and the vibration suppression speed are obtained.Finally，using the theory of sound radiation combined with the transient boundary element method，the characteristics of the transient noise of the beam induced by different train speeds are calculated and analyzed.The results show that the train-speed change can cause fluctuation of the displacement amplitude of the beam structure.The vibration acceleration of the beam structure increases with the increasing of the train speed.Variation of the radiation noise of the beam structure is somewhat correlated with that of the structure vibration acceleration.When the train is traveling through the beam bridge at the resonance speed，the dynamic response and the radiation noise of the structure will be obviously amplified.The transient noise of the beam bridge structure is also significant under resonant speed in the far acoustic field.So，the train speed should be controlled in order to reduce the noise of the beam bridge structure.

vibration and wave；trough-shaped beam；moving load；resonance；vibration suppression；transient sound radiation characteristic

U239.5；U491.91

ADOI編碼：10.3969/j.issn.1006-1335.2016.05.024

1006-1355（2016）05-0112-04

2016-03-06

國家自然科學基金資助項目（51268014）、（51578238）；江西省“贛鄱英才555工程”領軍人才培養計劃項目

劉林芽（1973-），男，江西省樟樹市人，教授，博士，博士生導師，主要研究方向為鐵路環境振動與噪聲。E-mail:316058254@qq.com