基于復雜追蹤理論的結構模態參數識別

尤傳雨，劉文波，常軍

（蘇州科技大學土木工程學院，江蘇蘇州215011）

基于復雜追蹤理論的結構模態參數識別

尤傳雨，劉文波，常軍

（蘇州科技大學土木工程學院，江蘇蘇州215011）

復雜追蹤（CP）是近期發展起來的一種結合信號統計特性和時序結構的盲源分離新算法，通過找到一個合適的投影方向，使其在該方向投影信號的復雜度最小，從而實現對混合信號的分離。通過CP技術將結構的響應信號分離，得到模態振型和模態響應，進而利用單模技術分析得到的結構模態參數。最后，采用一三層框架數值模型對該方法進行驗證，結果表明該算法可以準確有效地識別結構的模態參數。

盲源分離；復雜追蹤；時間預測；結構模態參數識別

近年來，盲源分離（BSS）已成為現代信號處理領域的熱點，在通信工程、語音處理、圖像處理等領域具有重要的理論意義和實際應用價值［1］。盲源分離在結構模態參數識別中的應用已取得了一定的成果，即在激勵未知的情況下，根據結構響應的統計特性，僅從觀測信號中分離出結構響應源信號，進而得到結構模態參數，為健康狀態評估提供重要依據［2－3］。然而，盲源分離技術在實際工程的應用存在一些不足，如獨立分量分析（ICA）算法無法有效識別高阻尼結構等［4－5］。

復雜追蹤（CP）是近期發展起來的一種BSS技術，該方法結合了信號的統計特性和時序結構，通過尋找合適的投影方向，使該方向投影信號的復雜度最小，從而實現對混合信號的分離。目前，一些學者將CP應用于圖像和語音處理［6］，而應用于模態參數識別的研究尚不多見。CP在模態參數識別中的應用是通過其分解觀測信號得到各階模態響應，完成結構動力響應從物理空間到模態空間的轉換，同時確定了結構的振型；接著，應用單模態識別技術從分離出的模態響應中，提取結構各階模態頻率和阻尼［7－8］。論文在詳細闡述CP基本原理的基礎上，通過數值算例對CP識別結構模態參數進行驗證。

1　復雜度追蹤

1.1復雜度追蹤基本原理

線性瞬時盲源分離模型［9－10］表示為

式中，t為時刻，x（t）為n個未知源信號混合而成的n維觀測信號，x（t）=［x1（t），x2（t），…xn（t）］T；A為未知的n×n維混合矩陣；s（t）為n個源信號組合而成，s（t）=［s1（t），s2（t），…sn（t）］T；

Stone認為任何源信號都是由某一質點按一定的物理規則隨著時間運動而產生的。因此，源信號可認為比混合信號更簡單，即源信號的復雜度小于由其混合而成的觀測信號復雜度［10］。

根據Stone理論，從混合信號中分離出具有最小復雜度的信號即可被認為是一條源信號。因此，復雜追蹤的目的就是尋找一個解混向量，使得分離成分擁有最小復雜度，即逼近最簡單的源信號。

1.2目標函數

統計學中，信號的復雜度都用Kolmogorov復雜度測得［11-12］。然而Kolmogorov復雜度具有不直觀、實際中很難估計等不足，因此Stone提出了一種簡單而且穩定性好的復雜度——時間預測，定義為

其中

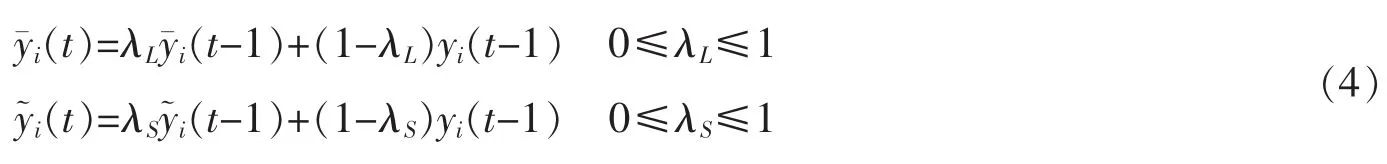
令λ=2-1/h，hS=1，hL為任意遠大于hS的值，如hL=900 000。V（·）用來衡量yi（t）的總體變化，表示yi（t）根據長期變化均值yˉi（t）預測得到的程度；相反，U（·）衡量的是yi（t）的局部平滑度，表示yi（t）根據短期變動均值y~i（t）預測得到的程度；因此，時間預測值F（·）利用了信號的統計特性和時間序列，把其為CP的目標函數，能夠分離具有時序結構的信號。

將式（2）代入（3）得

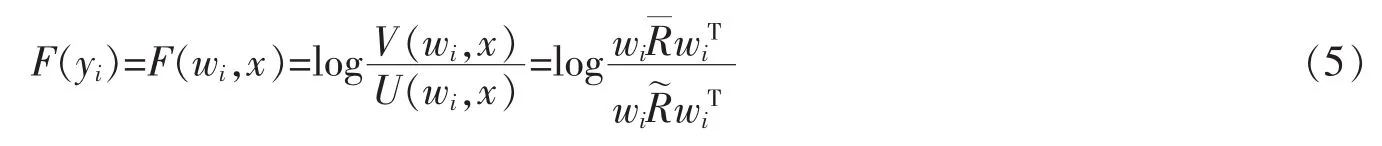
式中，R為混合信號的協方差矩陣，其元素定義為

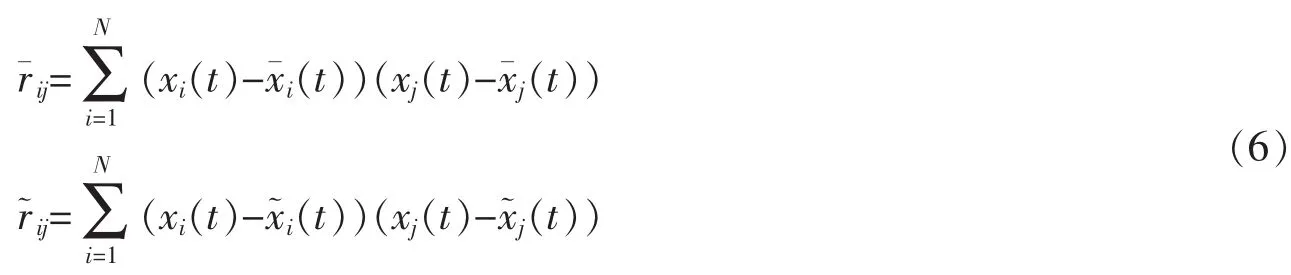
對時間預測函數兩邊求導得

令其等于零，得

2　CP識別結構模態參數

由動力學知識可知，線性振動系統的自由響應為

式中，qi為正規坐標，可表示為qi（t）=ai（t）sin（wdit+θi），wdi為有阻尼頻率，θi為相位角，對于自由響應：ai（t）為指數衰減函數exp（-ξiwdit），ξi、wdi分別為阻尼比與固有頻率；φi為固有振型向量；n為系統的模態數。模態參數識別的任務就是從響應信號x（t）中識別出振型矩陣Φ、各階頻率wi和阻尼比ξi。

對比式（1）和式（10）可得，A=Φ，s（t）=q（t），即可以把模態響應q（t）看作源信號，振型矩陣Φ看作源信號的混合矩陣，則結構自振響應信號x（t）是模態響應q（t）經過振型矩陣線性加權所得的混合信號（即觀測信號）［13］。CP識別結構模態參數流程如下：

（1）通過復雜追蹤理論，得到分離矩陣W，繼而求得振型Φ＝W-1；

（2）通過y（t）=Wx（t），從結構響應中分離出y（t），即模態響應q（t）。

（3）通過單自由度系統參數識別技術便可以從模態響應中識別出各階固有頻率和阻尼比。

3　數值分析

3.1自由響應

建立如圖1所示三層框架模型，采集結構自由振動響應信號，采樣頻率fz=100 Hz，時間取10 s，具體結構物理參數見表1，其中阻尼比按照Rayleigh阻尼進行設置。

圖1　三層框架模型

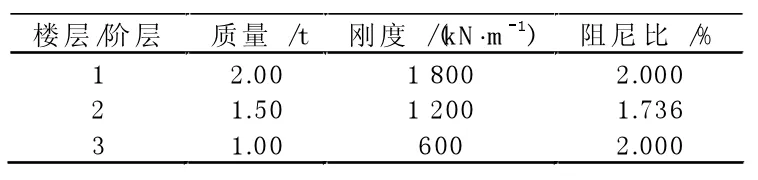
表1　三層框架模型結構特性

為了測量結構識別振型與理論振型的準確度，采用模態置信準則（Modal Assurance Criterion，MAC）作為衡量標準。MAC的表達式［14］為

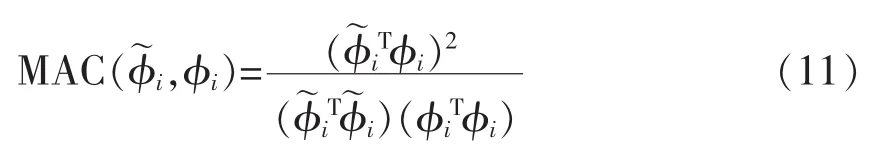
通過復雜追蹤技術直接處理結構的響應信號，圖2、圖4分別為結構的自振響應信號和分離得到的信號，圖3、圖5分別響應信號和分離信號作傅里葉變換所得。由圖4可以看出，CP算法分離出來的信號，均為自由衰減的簡諧信號，即可認為這些信號對應于各階的模態響應，繼而利用Hilbert變換，求出結構的頻率和阻尼比，結果見表2。振型圖見圖6。

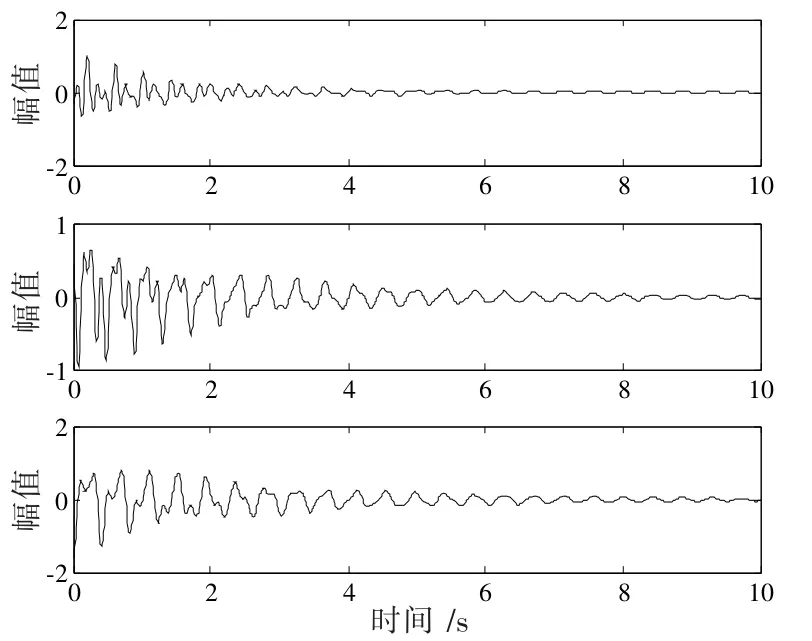
圖2　結構自由響應信號

圖3　自由響應快速傅里葉變換

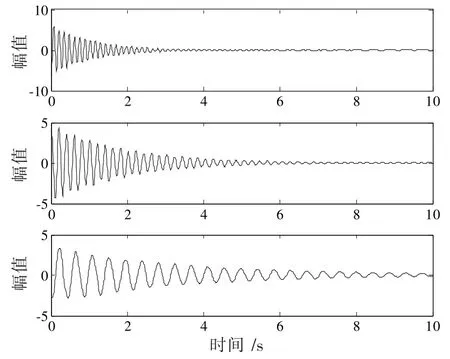
圖4　CP分離出的信號

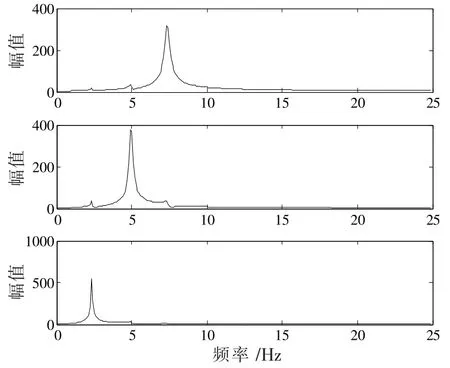
圖5　分離信號快速傅里葉變換

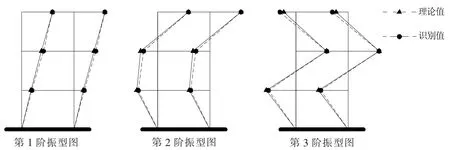
圖6　模態振型圖

表2　結構模態參數識別結果

由表2可以看出，模態振型的各階MAC值均接近于1，且識別出來的頻率和阻尼比與理論值相比較，誤差很小。因此，將復雜追蹤理論應用于識別結構自由響應下的模態參數是可行的。

3.2隨機響應

用穩態的高斯白噪聲對圖1框架進行激勵，采樣頻率fz=100 Hz，時間取100 s。復雜追蹤技術直接處理結構的響應信號，圖7、圖9分別為結構的隨機響應信號和分離得到的信號，圖8、圖10分別響應信號和分離信號作傅里葉變換所得。繼而利用Hilbert變換，求出結構的頻率和阻尼比，結果見表3。振型圖見圖11。

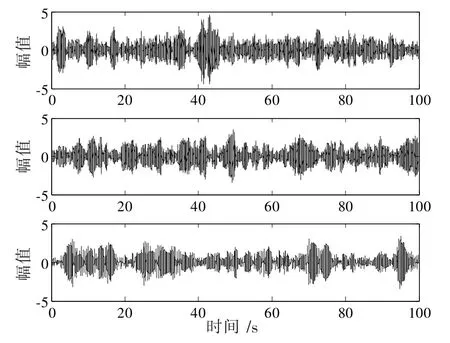
圖7　結構隨機響應信號

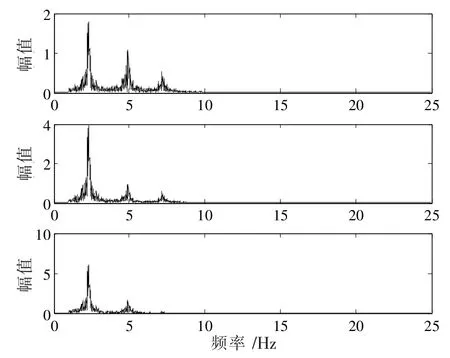
圖8　隨機響應快速傅里葉變換

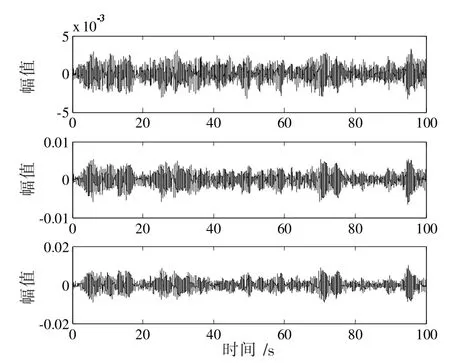
圖9　CP分離出的信號

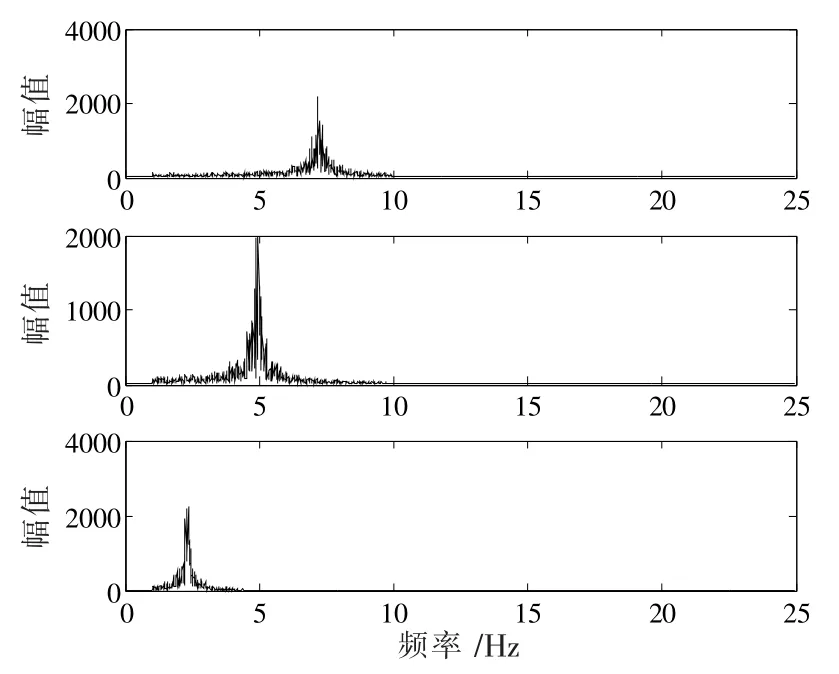
圖10　分離信號快速傅里葉變換

由表3可以看出，（1）由于隨機響應信號成分復雜且通常又是非平穩的，所以識別出的結構系統頻率大于自由響應，但仍與理論值吻合；（2）環境激勵作用下，結構系統阻尼受到破壞，需要通過外部激勵的特性進行準確識別，因此阻尼比識別誤差較大，可不予考慮；（3）模態振型的各階MAC值均在99.9%以上，表明算法較準確的分離出環境激勵下結構獨立源信號。因此，復雜追蹤理論能夠成功應用于隨機響應下的結構模態參數識別。

表3　結構模態參數識別結果

圖11　模態振型圖

4　結語

論文首先描述了復雜追蹤基本原理，理論上證明了該算法能夠成功分離混合信號。引入時間預測作為復雜追蹤的目標函數，并探討了采用CP算法識別結構模態參數的可行性。運用復雜追蹤算法對三層框架模型的自由響應信號和隨機響應信號進行處理，并采用Hilbert變換識別出結構的阻尼和頻率。自由響應中，模態參數識別精度高；隨機響應中，由于受到噪聲激勵的影響，模態參數識別精度有所降低，但識別誤差仍在可接受范圍內。因此，復雜追蹤理論能夠較好的應用于結構模態參數識別領域。

［1］畢楊.基于快速獨立分量分析的盲源分離算法研究及應用［D］.西安：西安理工大學，2007.

［2］靜行，袁海慶，趙毅.基于獨立分量分析的結構模態參數識別［J］.振動沖擊，2010，29（3）：137-141.

［3］李炎華，樊可清.獨立分量分析在模態分析中的應用［J］.計算機工程與應用，2009，45（3）：220-221.

［4］KERSCHEN G，PONCELET F，GOLINVAL J C.Physical interpretation of independent component analysis in structural dynamics［J］.Mechanical Systems and Signal Processing，2007，21（4）：1561-1575.

［5］MCNEIL S.Modal identification using blind source separation techniques［D］.Houston:University of Houston，2007.

［6］李兵，劉穎，葛正坤.基于復雜性尋蹤的非獨立圖像盲分離［J］.計算機工程與應用，2009，45（30）：168-170.

［7］韓建平，李達文，王飛行.基于Hilbert-Huang變換和隨機子空間識別的模態參數識別［J］.地震工程與工程振動，2010，30（1）：53-59.

［8］張曉丹.基于盲源分離技術的工程結構模態參數識別方法研究［D］.北京：北京交通大學，2010.

［9］YANG Yongchao，SATISH N.Blind modal identification of output-only structures in time-domain based on complexity pursuit［J］.Earthquake Engineering&Structural Dynamics，2013，42（13）：1885-1905.

［10］STONE J V.Blind source separation using temporal predictability［J］.Neural Computation，2001，13（7）：1559-1574.

［11］AAPO Hyv?rinen，ERKKI Oja.A fast fixed-point algorithm for independent component analysis［J］.Neural Computation，1997，9（7）：1483-1492.

［12］AAPO Hyv?rinen，ERKKI Oja.Independent component analysis:algorithms and applications［J］.Neural Networks，2000，13（4-5）：411-430.

［13］胡皞，常軍，劉文波，等.基于獨立成分分析的結構模態參數識別［J］.蘇州科技學院學報（工程技術版），2014，27（3）：40-45.

［14］曹樹謙，張文德，蕭龍翔.振動結構模態分析——理論、實驗與應用［M］.天津：天津大學出版社，2001.

Structural modal parameter identification based on complexity pursuit

YOU Chuanyu，LIU Wenbo，CHANG Jun
（School of Civil Engineering，SUST，Suzhou 215011，China）

Complexity pursuit（CP）is a newly developed blind source separation（BSS）of combining the signal statistical characteristics and temporal structure.The complexity of the signal can be reduced to the least by an appropriated project so as to realize the separation of the mixed signal.The structural modal shapes and single modal responses are gained by CP to separate the response signal and then to get the parameter of the structural modal by the single modal analysis.Finally，a numerical model of three-floor frame is used to identify the method，and the result shows that the model can accurately and feasibly identify the structural modal parameter.

blind source separation；complexity pursuit；temporal predictability；structural modal parameter identification

TU311

A

1672-0679（2016）02-0038-05

2015-08-31

江蘇省自然科學基金項目（BK20141180）；江蘇省結構工程重點實驗室開放課題（Z1405）；江蘇省建設系統科技項目（2015ZD77）

尤傳雨（1990-），男，江蘇盱眙人，碩士研究生。

通信聯系人：常軍（1973-），男，教授，博士，主要從事健康監測與振動控制研究，Email：changjun21@mail.usts.edu.cn。

（責任編輯：經朝明）