基于自適應(yīng)動態(tài)規(guī)劃的礦渣微粉生產(chǎn)過程跟蹤控制
王康 李曉理 賈超 宋桂芝
基于自適應(yīng)動態(tài)規(guī)劃的礦渣微粉生產(chǎn)過程跟蹤控制
王康1李曉理2賈超1宋桂芝3
礦渣微粉是一種新型綠色環(huán)保型建材,可以大大提高水泥混凝土的力學(xué)性能.本文以礦渣微粉生產(chǎn)過程為研究對象,針對該過程難以通過機(jī)理建模進(jìn)行辨識和控制的特點(diǎn),利用數(shù)據(jù)驅(qū)動的思想,建立礦渣微粉生產(chǎn)過程的遞歸神經(jīng)網(wǎng)絡(luò)模型.在此基礎(chǔ)上,利用自適應(yīng)動態(tài)規(guī)劃,設(shè)計(jì)具有控制約束的跟蹤控制器,并將其應(yīng)用到礦渣微粉生產(chǎn)過程中.仿真分析表明,建立的數(shù)據(jù)驅(qū)動模型能夠有效地辨識礦渣微粉生產(chǎn)過程,同時(shí),本文提出的控制方法能夠?qū)崿F(xiàn)輸入受限的微粉比表面積及磨內(nèi)壓差的最優(yōu)跟蹤控制.
礦渣微粉,數(shù)據(jù)驅(qū)動,自適應(yīng)動態(tài)規(guī)劃,最優(yōu)跟蹤控制,輸入有界
引用格式王康,李曉理,賈超,宋桂芝.基于自適應(yīng)動態(tài)規(guī)劃的礦渣微粉生產(chǎn)過程跟蹤控制.自動化學(xué)報(bào),2016,42(10): 1542-1551
礦渣粉磨生產(chǎn)是一個(gè)復(fù)雜多變量、強(qiáng)耦合的非線性過程,實(shí)質(zhì)是將廢棄礦渣經(jīng)過粉磨,及時(shí)選出物料中達(dá)到一定粒徑要求的微粉.高爐礦渣廢棄物經(jīng)過粉磨,比表面積在400m2/kg以上的細(xì)粉稱為礦渣微粉.礦渣微粉可以部分代替水泥,以礦物參合料的形式參與混凝土配置,大大提高水泥混凝土的力學(xué)性能[1-2].近年來,建筑業(yè)對高質(zhì)量的礦渣微粉需求十分緊迫,然而在實(shí)際生產(chǎn)過程中,高效率地生產(chǎn)超細(xì)礦渣微粉還面臨許多控制上的難題.例如,微粉的比表面積往往會受到風(fēng)速、電機(jī)轉(zhuǎn)速、壓力、溫度等多方面因素的影響,礦渣粉磨系統(tǒng)的復(fù)雜性造成了對其進(jìn)行有效控制十分困難.實(shí)際生產(chǎn)過程中,往往是憑借工人經(jīng)驗(yàn)、長期監(jiān)控設(shè)備狀態(tài)和及時(shí)調(diào)整控制參數(shù)實(shí)現(xiàn)生產(chǎn)控制.然而由于工人操作水平參差不齊,往往造成產(chǎn)品質(zhì)量波動較大.如何建立微粉生產(chǎn)過程的有效模型,并在此基礎(chǔ)上實(shí)現(xiàn)生產(chǎn)過程的高效自動控制,是一個(gè)極為重要的研究方向.
礦渣粉磨是一個(gè)多變量、強(qiáng)耦合、非線性的生產(chǎn)過程,并且立磨內(nèi)部存在復(fù)雜的物理化學(xué)變化,難以建立整個(gè)微粉生產(chǎn)過程的準(zhǔn)確機(jī)理模型.陳遠(yuǎn)[3]對立磨中微粉顆粒進(jìn)行了流體力學(xué)分析,并討論了產(chǎn)品細(xì)度與各單一變量之間的關(guān)系,對揭示立磨內(nèi)部現(xiàn)象和粉磨機(jī)理起到了重要作用,但由于產(chǎn)品細(xì)度受到多變量的影響,難以建立生產(chǎn)過程的完整機(jī)理模型.另一方面,立磨粉磨過程中,具有豐富的離線和在線數(shù)據(jù),例如主電機(jī)電流、磨機(jī)壓差、選粉機(jī)轉(zhuǎn)速、入磨溫度、比表面積等,這些數(shù)據(jù)僅被工人記錄并作為檢修參考數(shù)據(jù),并沒有得到很好的利用和挖掘.
數(shù)據(jù)驅(qū)動控制不依靠生產(chǎn)過程的系統(tǒng)模型信息,僅利用在線和離線數(shù)據(jù)便能實(shí)現(xiàn)輸出變量和過程可測變量之間的建模與控制[4-6].對于水泥生產(chǎn)過程中的立磨粉磨系統(tǒng),數(shù)據(jù)驅(qū)動控制正在被廣泛研究,試圖對復(fù)雜的粉磨系統(tǒng)進(jìn)行準(zhǔn)確辨識,以實(shí)現(xiàn)高效控制.針對料層厚度與喂料量、磨機(jī)出口溫度與熱風(fēng)閥開度之間的關(guān)系,顏文俊等[7]采用最小二乘法建立了立磨控制回路模型,并采用預(yù)測控制方法實(shí)現(xiàn)了優(yōu)化控制.Cai等[8]對水泥粉磨系統(tǒng)采用最小二乘支持向量機(jī)方法,建立了料層厚度的軟測量模型,實(shí)現(xiàn)了料層厚度的間接測量.Lin等[9]采用小波神經(jīng)網(wǎng)建立了立磨粉磨模型,并通過蟻群算法實(shí)現(xiàn)參數(shù)最優(yōu)設(shè)置.Umucu等[10]利用多層感知器神經(jīng)網(wǎng)和徑向基函數(shù)神經(jīng)網(wǎng),建立了水泥粒度模型,并獲得了較高的預(yù)測精度.
作為一種數(shù)據(jù)驅(qū)動控制方法,自適應(yīng)動態(tài)規(guī)劃(Adaptive dynamic programming,ADP)利用離線和在線數(shù)據(jù),采用神經(jīng)網(wǎng)絡(luò)逼近動態(tài)規(guī)劃中的性能指標(biāo)函數(shù)和控制策略,進(jìn)而滿足最優(yōu)性原理[11-12].自適應(yīng)動態(tài)規(guī)劃解決了傳統(tǒng)動態(tài)規(guī)劃中的“維數(shù)災(zāi)”難題,為求解非線性系統(tǒng)的最優(yōu)控制提供了一種切實(shí)可行的控制方案.2002年,Murray等[13]首先提出了針對連續(xù)系統(tǒng)的迭代ADP算法.迭代ADP通過策略迭代和值迭代來更新策略方程和值函數(shù)[14-15].然而迭代ADP算法往往迭代次數(shù)不確定,計(jì)算時(shí)間較長且計(jì)算量大,一旦系統(tǒng)發(fā)生變化,需要重新進(jìn)行離線計(jì)算.近年來,在線ADP算法[16-17]被廣泛提出,這些在線算法不需要進(jìn)行離線迭代計(jì)算,能夠通過在線自適應(yīng)的方式獲得最優(yōu)控制問題的解.實(shí)際生產(chǎn)過程中,各執(zhí)行機(jī)構(gòu)變量往往會受到范圍約束,存在飽和非線性.本文將在線自適應(yīng)ADP應(yīng)用到礦渣微粉生產(chǎn)過程中,在輸入受約束的前提下,設(shè)計(jì)輸入受限的在線ADP跟蹤控制器,實(shí)現(xiàn)生產(chǎn)過程的最優(yōu)跟蹤控制.
針對礦渣微粉生產(chǎn)難以機(jī)理建模的特點(diǎn),本文深入研究礦渣微粉生產(chǎn)過程機(jī)理,分析并給出了系統(tǒng)的非線性動態(tài)過程結(jié)構(gòu).采用遞歸神經(jīng)網(wǎng),建立基于數(shù)據(jù)的生產(chǎn)過程的辨識模型.根據(jù)辨識模型,采用在線自適應(yīng)動態(tài)規(guī)劃的方法,實(shí)現(xiàn)了礦渣微粉生產(chǎn)過程輸入有界的最優(yōu)跟蹤控制.本文結(jié)構(gòu)如下:第1節(jié)分析礦渣微粉生產(chǎn)流程并給出系統(tǒng)動態(tài)方程描述;第2節(jié)建立微粉生產(chǎn)過程的數(shù)據(jù)驅(qū)動模型,并在此基礎(chǔ)上設(shè)計(jì)基于ADP的輸入有界跟蹤控制器;第3節(jié)將提出的建模和控制方法應(yīng)用到礦渣微粉生產(chǎn)過程中,驗(yàn)證方法的有效性;第4節(jié)對全文進(jìn)行總結(jié).
1 礦渣微粉生產(chǎn)過程
1.1礦渣微粉生產(chǎn)流程
礦渣粉磨生產(chǎn)是將廢棄礦渣經(jīng)過粉磨,及時(shí)選出物料中達(dá)到一定粒徑要求的微粉.比表面積為400m2/kg以上的礦渣微粉可以部分代替水泥,以礦物參合料的形式配置混凝土,從而大大提高水泥混凝土的力學(xué)性能.
礦渣微粉生產(chǎn)系統(tǒng)主要由喂料皮帶稱、立磨機(jī)、物料傳送帶、收塵器、風(fēng)機(jī)等設(shè)備構(gòu)成.礦渣原料經(jīng)過預(yù)處理,由稱量皮帶進(jìn)行稱量并由傳送皮帶傳送至立磨,原料由于磨盤旋轉(zhuǎn)的離心力作用,在粉磨過程中移向磨盤邊緣,在磨盤和磨輥之間的擠壓下進(jìn)行粉磨.自下而上的熱風(fēng)將物料吹起烘干,同時(shí)將物料提送至磨機(jī)上部進(jìn)行篩選,符合粒度要求的物料被抽出立磨進(jìn)行收集,沒有被選出的粗顆粒被重新粉磨,其現(xiàn)場生產(chǎn)實(shí)時(shí)監(jiān)控畫面及工藝流程如圖1和圖2所示.
1.2礦渣微粉生產(chǎn)系統(tǒng)分析
礦渣微粉生產(chǎn)系統(tǒng)的控制目標(biāo)是在保證礦渣微粉質(zhì)量的同時(shí),最大限度地降低立磨振動,以保證生產(chǎn)過程平穩(wěn)運(yùn)行.
1.2.1磨機(jī)振動
影響立磨穩(wěn)定運(yùn)行的因素很多,立磨振動是最常見也是對立磨運(yùn)行影響最大的一種異常工況.根據(jù)微粉粉磨生產(chǎn)的控制要求,立磨振動值僅允許在給定的范圍內(nèi)變動,超出該范圍就可能引起立磨停機(jī)等故障.影響立磨振動的因素主要有磨內(nèi)壓差、磨內(nèi)溫度及選粉機(jī)轉(zhuǎn)速等.
1)磨內(nèi)壓差.磨內(nèi)壓差是指在粉磨過程中,磨腔選粉機(jī)下部與熱風(fēng)入口處靜壓之差.壓差的變化直接反映了立磨內(nèi)循環(huán)物料量的變化.正常情況下,磨內(nèi)壓差是穩(wěn)定的,標(biāo)志著入磨物料量和出磨物料量達(dá)到了動態(tài)平衡.壓差低于穩(wěn)定值表明物料入磨量小于出磨量,料層厚度降低,直至立磨因空磨而振動停機(jī);壓差高于穩(wěn)定值表明物料入磨量大于出磨量,嚴(yán)重時(shí)導(dǎo)致料層不穩(wěn)定或吐渣嚴(yán)重,造成飽磨而振動停機(jī).一般情況下,磨內(nèi)壓差可以通過調(diào)整喂料量來進(jìn)行調(diào)節(jié).實(shí)際生產(chǎn)過程中,磨內(nèi)壓差一般維持在20~35mbar,并以磨內(nèi)壓差作為立磨振動大小及立磨穩(wěn)定運(yùn)行的指標(biāo).
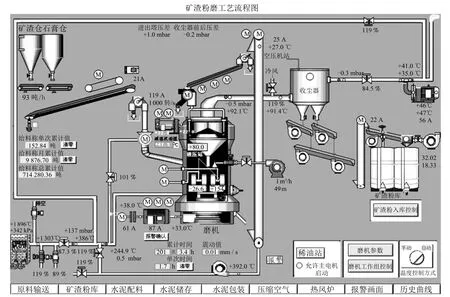
圖1 礦渣微粉生產(chǎn)監(jiān)控畫面Fig.1 Monitor screen of slag grinding process
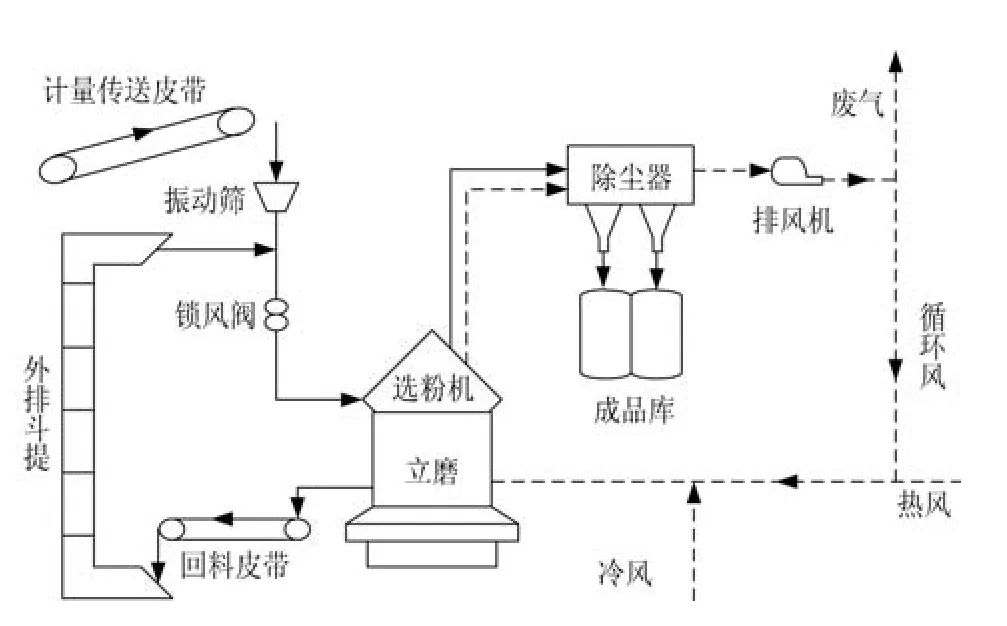
圖2 礦渣微粉生產(chǎn)流程圖Fig.2 Flow chart of slag grinding process
2)磨內(nèi)溫度.磨內(nèi)溫度過高,會造成磨內(nèi)上部物料由于靜電作用而大規(guī)模聚集,掉入磨盤底部進(jìn)行重新粉磨,從而造成立磨振動值增大.入磨熱風(fēng)溫度是影響磨內(nèi)溫度的主要因素.
3)選粉機(jī)轉(zhuǎn)速.選粉機(jī)轉(zhuǎn)速過快,大量微粉物料因不能滿足細(xì)度要求而落入磨內(nèi)重新研磨,導(dǎo)致磨內(nèi)物料增多,磨內(nèi)壓差增大,引起立磨振動.選粉機(jī)轉(zhuǎn)速一般要求小于1250r/min.
1.2.2微粉比表面積
微粉比表面積是衡量礦渣微粉產(chǎn)品質(zhì)量(即產(chǎn)品細(xì)度)的重要指標(biāo),當(dāng)高爐礦渣細(xì)磨成比表面積為400m2/kg以上時(shí),可以以20%~70%的比例替代水泥,以礦物摻合料的形式參與混凝土配置,大大提高了水泥混凝土力學(xué)性能.超細(xì)礦渣微粉是指比表面積達(dá)到500m2/kg以上更為細(xì)化的礦渣微粉,其活性較普通的礦渣微粉更強(qiáng),具有水化熱低、耐腐蝕、與鋼筋粘結(jié)力強(qiáng)、后期強(qiáng)度高、防微縮等特點(diǎn).影響微粉比表面積的因素主要有:
1)入磨物料.入磨物料的硬度、含水量等直接影響礦渣微粉的產(chǎn)量,同時(shí)也是影響產(chǎn)品細(xì)度的重要參數(shù).
2)入磨熱風(fēng).入磨熱風(fēng)不僅對立磨內(nèi)物料進(jìn)行烘干,而且將粉磨后物料提升至選粉區(qū)域進(jìn)行選粉,熱分的風(fēng)量、風(fēng)速以及出入磨風(fēng)溫等對選粉機(jī)的產(chǎn)量和產(chǎn)品細(xì)度都有著重要影響.在風(fēng)速一定的前提下,風(fēng)量過大或過小都會影響產(chǎn)品細(xì)度.磨內(nèi)風(fēng)量增大,則產(chǎn)品細(xì)度變粗,微粉產(chǎn)量增大,同時(shí)造成磨內(nèi)回料量增多,料層穩(wěn)定性變小;磨內(nèi)風(fēng)量過小,導(dǎo)致產(chǎn)品細(xì)度變細(xì),產(chǎn)量降低,同時(shí)由于磨內(nèi)顆粒濕度增加,造成回料量增多.磨內(nèi)風(fēng)量一般通過控制入磨循環(huán)風(fēng)閥開度來進(jìn)行調(diào)節(jié).
3)選粉機(jī)轉(zhuǎn)速.選粉機(jī)轉(zhuǎn)速是直接影響微粉生產(chǎn)產(chǎn)量和產(chǎn)品細(xì)度的重要參數(shù).在選粉機(jī)分級力場中,微粉顆粒主要受到兩個(gè)力的作用:選粉機(jī)轉(zhuǎn)速決定的離心力Fu和風(fēng)速決定的徑向方向上氣流對顆粒的阻力Fr.如圖3所示,當(dāng)Fu>Fr時(shí),顆粒向邊壁沉降,成為粗粉進(jìn)一步粉磨;當(dāng)Fu<Fr時(shí),顆粒在氣流的攜帶作用下穿過分級面形成細(xì)粉.選粉機(jī)轉(zhuǎn)速越快,離心力越大,產(chǎn)品細(xì)度越細(xì).在實(shí)際生產(chǎn)過程中,出磨風(fēng)量及風(fēng)速變化不大,控制選粉機(jī)轉(zhuǎn)速是控制產(chǎn)品細(xì)度的重要手段.立磨選粉機(jī)轉(zhuǎn)子采用了變頻調(diào)速系統(tǒng),能夠?qū)崿F(xiàn)平滑調(diào)速,從而更好地控制產(chǎn)品細(xì)度.
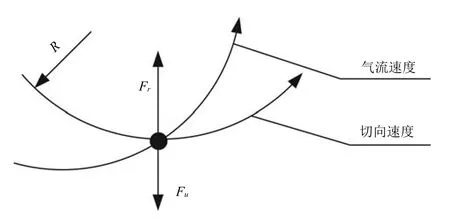
圖3 微粉顆粒受力圖Fig.3 Stress analysis of slag powder
通過以上分析可知,礦渣微粉的產(chǎn)量和質(zhì)量,以及立磨的正常運(yùn)行,受到磨內(nèi)壓差、料層厚度、喂料量、入磨循環(huán)風(fēng)閥開度、選粉機(jī)轉(zhuǎn)速等諸多參數(shù)的影響.這些參數(shù)之間具有很強(qiáng)的耦合性,互相影響、互相制約.
1.3礦渣粉磨系統(tǒng)動態(tài)方程描述
通過對礦渣粉磨系統(tǒng)進(jìn)行機(jī)理分析,磨機(jī)控制過程主要與以下參數(shù)有關(guān):
1)主要被控量,如比表面積s、磨內(nèi)壓差pd等;
2)主要控制量,如喂料量m、選粉機(jī)轉(zhuǎn)速v、入磨熱風(fēng)溫度T及入磨循環(huán)風(fēng)閥開度p.同時(shí)還受到礦渣濕度、熱風(fēng)風(fēng)量、入口負(fù)壓等參數(shù)θ的影響.
系統(tǒng)動態(tài)過程可描述為

其中,u=[u1,u2,u3,u4]T,x=[x1,x2]T,u1=m,u2=v,u3=T,u4=p,x1=s,x2=pd,θ為常數(shù).
在控制器的設(shè)計(jì)過程中,既要保證系統(tǒng)的穩(wěn)定性、收斂性和對設(shè)定值的有效跟蹤,又要保證控制器設(shè)計(jì)的可實(shí)施性.在實(shí)際生產(chǎn)過程中,各執(zhí)行器受到自身物理?xiàng)l件的約束,各輸入變量不能任意選取,只能在給定范圍內(nèi)取值;從生產(chǎn)工藝來看,立磨要穩(wěn)定運(yùn)行,其熱風(fēng)溫度、喂料量、選粉機(jī)轉(zhuǎn)速等運(yùn)行參數(shù)也必須保持在一定范圍內(nèi)波動.因此,往往獲得的最優(yōu)控制并不是理論上的最優(yōu)值,而是滿足約束條件(2)的次優(yōu)控制.
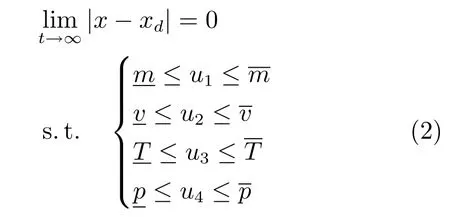
其中,xd為被控量的期望值為各控制量的變化范圍.
2 基于ADP的輸入有界跟蹤控制器設(shè)計(jì)
從被控對象的數(shù)學(xué)模型描述(1)來看,由于礦渣微粉生產(chǎn)系統(tǒng)具有可控變量多、各變量之間耦合性強(qiáng)、系統(tǒng)非線性等特點(diǎn),難以通過機(jī)理分析的方法建立全系統(tǒng)的精確數(shù)學(xué)模型.本文利用生產(chǎn)過程中的大量數(shù)據(jù),建立有效的數(shù)據(jù)驅(qū)動模型.并在此基礎(chǔ)上,考慮控制約束條件(2),設(shè)計(jì)在線ADP控制策略,在保證系統(tǒng)穩(wěn)定的前提下,提高產(chǎn)品質(zhì)量,實(shí)現(xiàn)微粉生產(chǎn)過程的最優(yōu)跟蹤控制.
2.1數(shù)據(jù)驅(qū)動建模
基于輸入輸出數(shù)據(jù),采用遞歸神經(jīng)網(wǎng)(Recursive neural network,RNN)[16],系統(tǒng)(1)可以寫成仿射非線性的形式
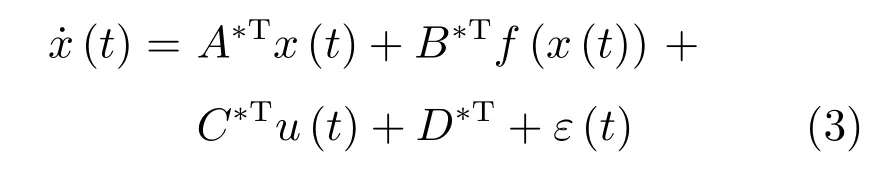
其中,系統(tǒng)狀態(tài)x∈Rn,控制輸入u∈Rm,A?,B?,C?,D?為未知的理想神經(jīng)網(wǎng)權(quán)值矩陣,模型重建誤差ε(t)是有界的.激活函數(shù)f(·)為單調(diào)遞增函數(shù),且對于任意的x,y∈R,x≥y,存在k>0滿足
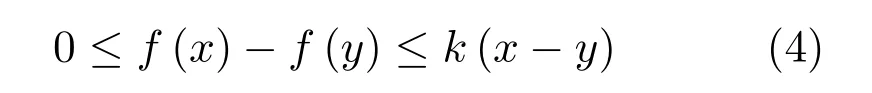
式中,‖f(x)‖≤bf‖x‖,其中bf為正常數(shù).本文令f(x)=tanh(x).
根據(jù)式(3),可以構(gòu)建數(shù)據(jù)驅(qū)動模型
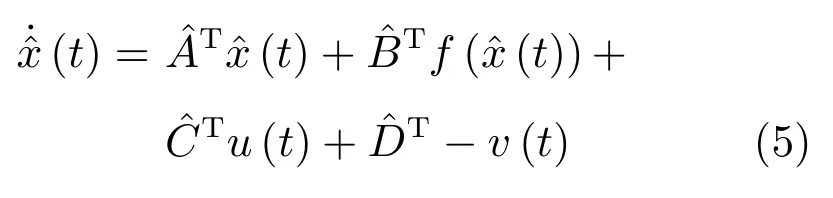
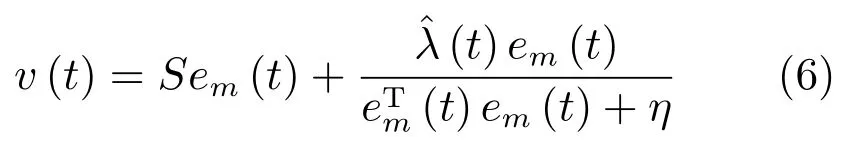
結(jié)合式(3)和式(5),可推導(dǎo)出模型誤差動態(tài)方程
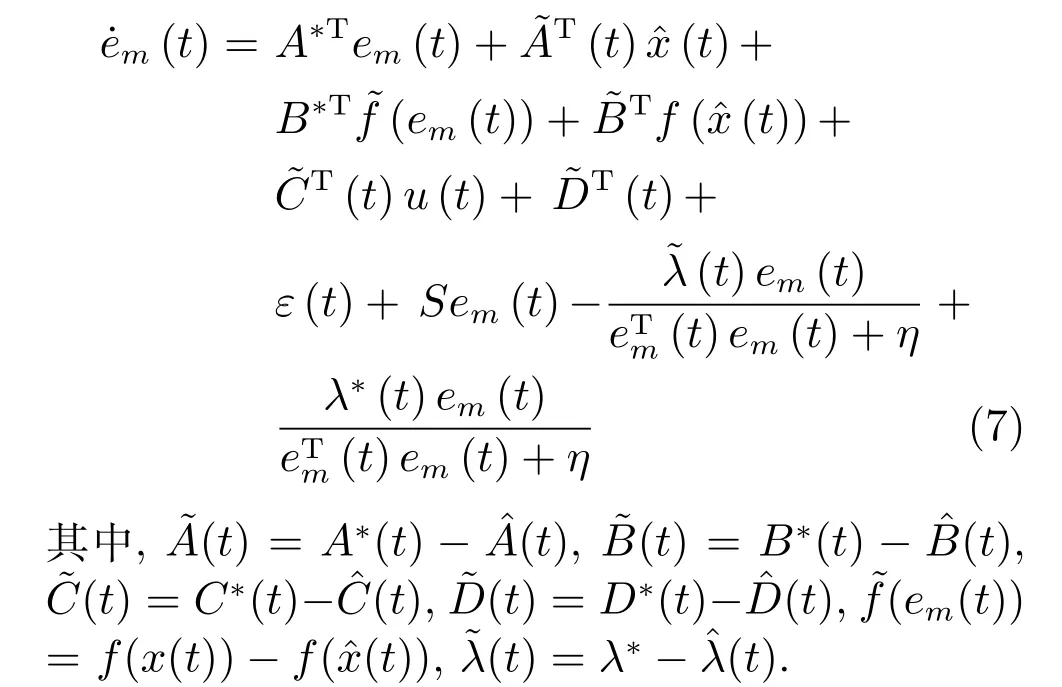
引理1[16].若數(shù)據(jù)驅(qū)動模型(5)的網(wǎng)絡(luò)權(quán)值矩陣和調(diào)節(jié)參數(shù)按照如下學(xué)習(xí)律進(jìn)行更新:
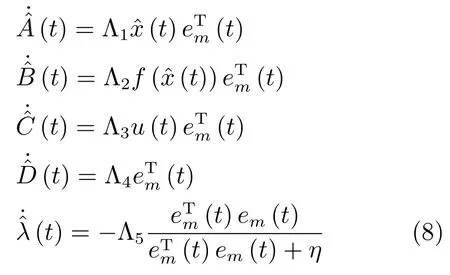
其中,Λi,i=1,2,···,5為相應(yīng)維數(shù)的正定矩陣,則模型辨識誤差漸近收斂,即limt→∞em(t)=0.且當(dāng)t→∞時(shí),分別趨近于常值矩陣A,B,C,D.
因此,采用大量離線數(shù)據(jù),經(jīng)過足夠長時(shí)間的模型辨識,非線性系統(tǒng)(1)可表示為
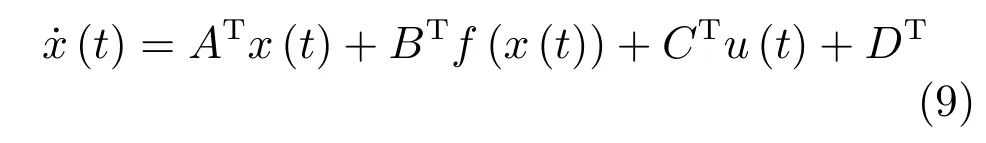
2.2輸入受限的ADP跟蹤控制器設(shè)計(jì)
針對遞歸神經(jīng)網(wǎng)模型(9),本小節(jié)采用特殊指標(biāo)函數(shù)解決輸入有界問題,采用評價(jià)網(wǎng)逼近指標(biāo)函數(shù),采用執(zhí)行網(wǎng)逼近最優(yōu)控制,從而設(shè)計(jì)出滿足控制約束的ADP跟蹤控制器.
2.2.1問題描述
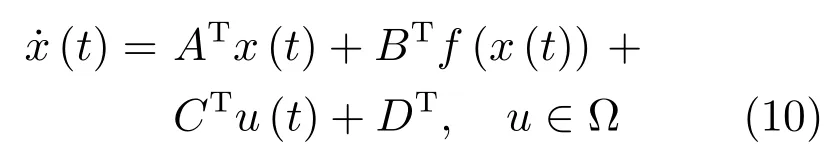
假設(shè)期望狀態(tài)軌跡為xd(t),由式(10)可得:
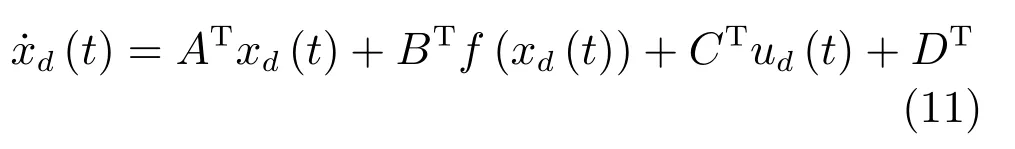
其中,ud(t)為期望輸入量,可通過下式直接計(jì)算獲得:
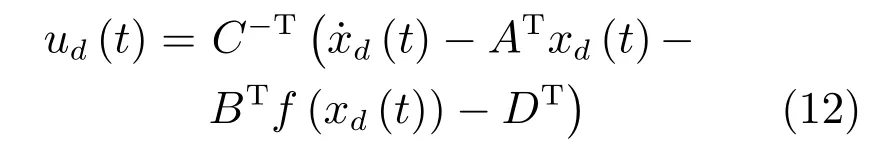
其中,C-T=C(CTC)-1為C的偽逆.
定義狀態(tài)誤差e(t)=x(t)-xd(t).根據(jù)式(10)和式(11),誤差系統(tǒng)可以寫成
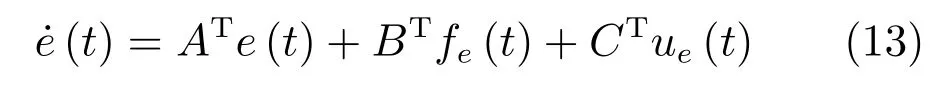
其中,fe(t)=f(x(t))-f(xd(t)),ue(t)=u(t)-ud(t).下文中e(t),u(t),ue(t),ud(t)將分別簡寫為e,u,ue,ud.
根據(jù)式(10),令ue滿足約束條件
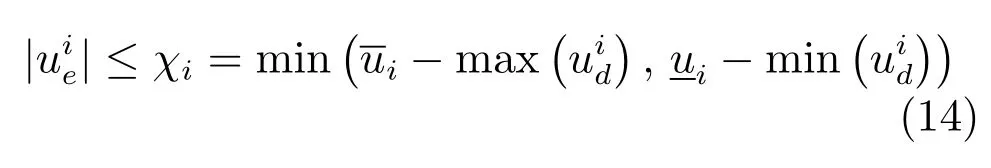
對于帶有約束的最優(yōu)跟蹤控制問題,其目標(biāo)是尋找滿足約束條件的最優(yōu)控制律ue(t),使得系統(tǒng)(13)漸近穩(wěn)定,使?fàn)顟B(tài)誤差e漸近收斂到零,并且能夠使如下性能指標(biāo)函數(shù)最小:

其中,效用函數(shù)r(e,ue)=Q(e)+W(ue).通常,和R為對稱正定矩陣.由于要求控制輸入有界,采用
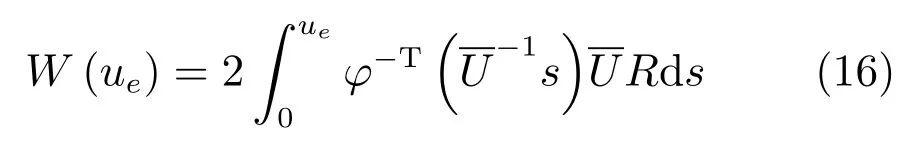
其中,R為對角正定矩陣,s∈Rm,?(·)∈Rm為單調(diào)遞增的有界奇函數(shù),滿足|?(·)|≤1,且其一階導(dǎo)數(shù)的界為常數(shù),?-1(·)表示?(·)的反函數(shù),?-T=(?-1)T.由于?-1(·)為單調(diào)奇函數(shù)且R是正定對角陣,故W(ue)也是正定的.不失一般性,本文令?(·)=tanh(·),R為m維單位矩陣.
定義如下Hamilton函數(shù):
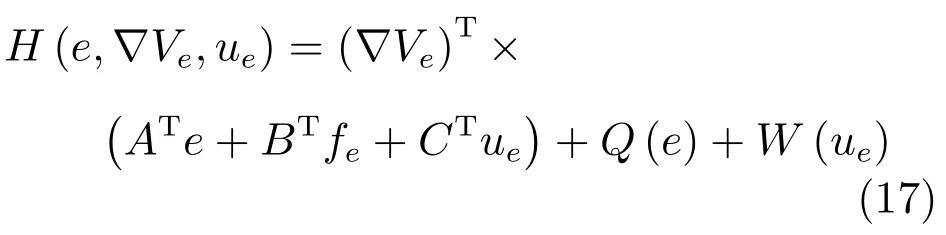
定義1[18].若ue(e)在?上連續(xù),ue(0)=0,ue(e)能夠使系統(tǒng)(13)在?上穩(wěn)定,并且對于任意的e∈?,V(ue(0))都是有界的,則稱控制量ue(e):Rn→Rm對于?上的函數(shù)(15)是容許的,記作ue∈ψ(?).
定義最優(yōu)指標(biāo)函數(shù)
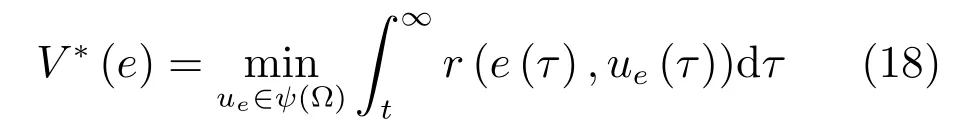
滿足如下HJB方程:

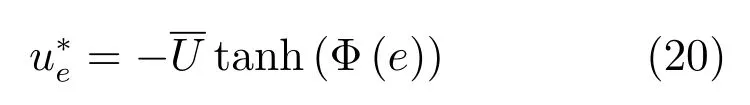
2.2.2基于ADP的跟蹤控制器設(shè)計(jì)
為了實(shí)現(xiàn)基于ADP的輸入有界最優(yōu)跟蹤控制,分別設(shè)計(jì)評價(jià)網(wǎng)絡(luò)和執(zhí)行網(wǎng)絡(luò).
1)評價(jià)網(wǎng)絡(luò).根據(jù)前饋神經(jīng)網(wǎng)的全局逼近特性,指標(biāo)函數(shù)可以通過如下網(wǎng)絡(luò)精確表示:
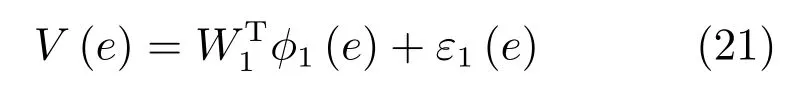
其中,W1∈RN1為理想評價(jià)網(wǎng)絡(luò)權(quán)值,N1為神經(jīng)元個(gè)數(shù),φ1(e)=[φ11(e),φ12(e),···,φ1N1(e)]T∈RN1為激活函數(shù)向量,ε1(e)為有界評價(jià)網(wǎng)逼近誤差,假設(shè)其對于e的一階偏導(dǎo)也是有界的.
指標(biāo)函數(shù)V(e)對于e求導(dǎo),可得:
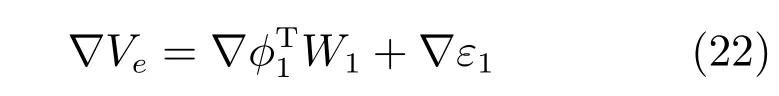
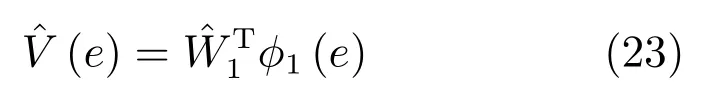
根據(jù)式(17)和式(23),可以推導(dǎo)出如下逼近的Hamilton函數(shù):
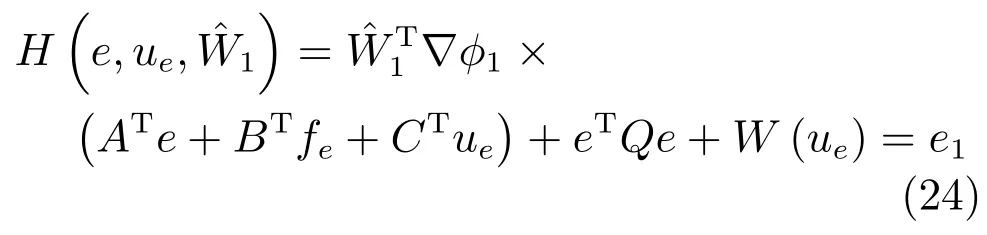
評價(jià)網(wǎng)絡(luò)的目標(biāo)是極小化如下目標(biāo)函數(shù):
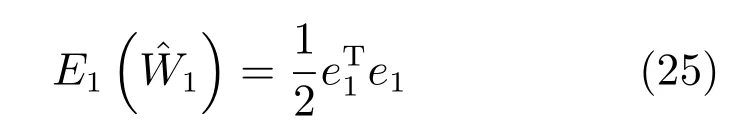
根據(jù)梯度下降法,評價(jià)網(wǎng)的權(quán)值更新法則可以表示為
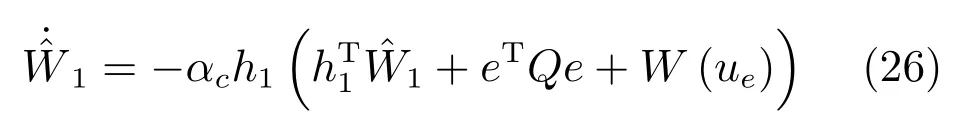
其中,αc>0為評價(jià)網(wǎng)的學(xué)習(xí)率,
2)執(zhí)行網(wǎng)絡(luò).為了求得嚴(yán)格受約束的反饋控制策略,通過執(zhí)行網(wǎng)絡(luò)逼近函數(shù)Φ(e):
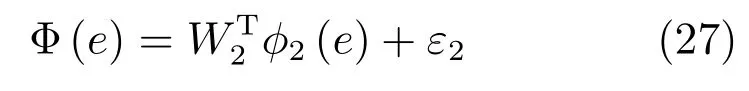
其中,W2∈RN2×m為執(zhí)行網(wǎng)的未知理想權(quán)值矩陣,φ2(e)∈RN2為執(zhí)行網(wǎng)激活函數(shù),N2為神經(jīng)元個(gè)數(shù),ε2為執(zhí)行網(wǎng)逼近誤差.
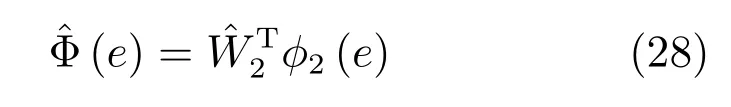
根據(jù)式(20)和式(23),執(zhí)行網(wǎng)絡(luò)的誤差函數(shù)為
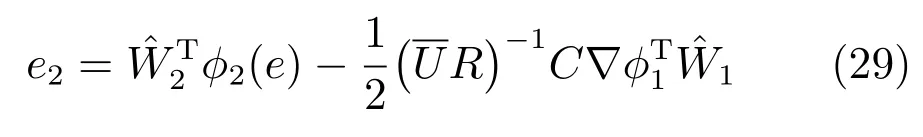
執(zhí)行網(wǎng)絡(luò)的目標(biāo)是使如下的目標(biāo)函數(shù)極小化:
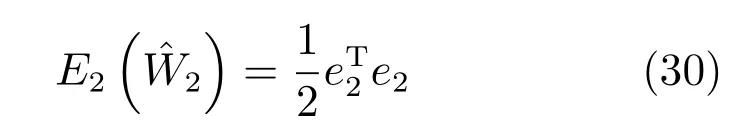
根據(jù)梯度下降法,執(zhí)行網(wǎng)絡(luò)的權(quán)值更新律可以表示為
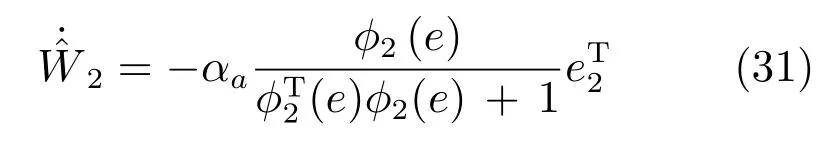
其中,αa為執(zhí)行網(wǎng)絡(luò)的學(xué)習(xí)率.執(zhí)行網(wǎng)輸出可表示為
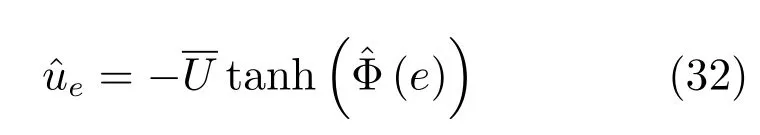
對于帶有控制約束的系統(tǒng)(10),采用上述方法設(shè)計(jì)的ADP最優(yōu)控制器,有如下定理成立.
定理1.對于如式(13)描述的帶有控制約束的非線性系統(tǒng),如果給定合適的學(xué)習(xí)律αc,αa,采用式(23)和式(28)描述的評價(jià)網(wǎng)和執(zhí)行網(wǎng),且其權(quán)值分別按照式(26)和式(31)在線調(diào)整,則當(dāng)神經(jīng)元個(gè)數(shù)足夠多時(shí),系統(tǒng)狀態(tài)誤差e及評價(jià)網(wǎng)和執(zhí)行網(wǎng)的估計(jì)誤差均一致最終有界.
根據(jù)文獻(xiàn)[19]中的收斂性證明過程,易證對于誤差系統(tǒng)(13),定理1成立,具體過程從略.
3 仿真分析
本文以濟(jì)南魯新新型建材股份有限公司3號礦渣微粉生產(chǎn)線采集的數(shù)據(jù)為研究對象,驗(yàn)證上述基于數(shù)據(jù)驅(qū)動的建模與最優(yōu)跟蹤控制的有效性.
3.1實(shí)驗(yàn)數(shù)據(jù)及預(yù)處理
實(shí)驗(yàn)針對3號礦渣微粉生產(chǎn)線運(yùn)行數(shù)據(jù),每隔2min進(jìn)行采樣,共獲得325組實(shí)驗(yàn)數(shù)據(jù),如表1所示.由于測量誤差或人為因素等原因,直接從現(xiàn)場獲得的數(shù)據(jù)中不可避免地存在顯著誤差.當(dāng)采樣點(diǎn)的值與均值的偏差大于三倍標(biāo)準(zhǔn)差時(shí),刪除該點(diǎn)數(shù)據(jù)以消除顯著誤差.同時(shí),對最終得到的250組數(shù)據(jù)進(jìn)行歸一化處理.
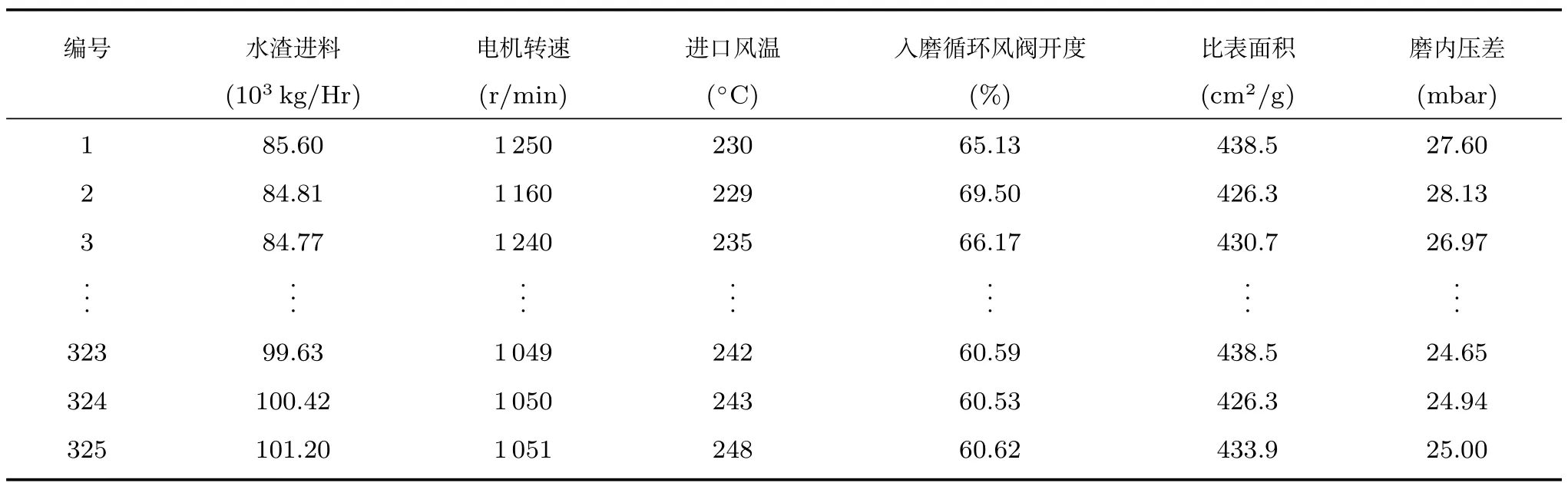
表1 濟(jì)鋼魯新建材3號礦渣微粉生產(chǎn)線生產(chǎn)運(yùn)行數(shù)據(jù)Table 1 Production data of Luxin mill line 3
由前述分析可知,礦渣微粉生產(chǎn)過程是一個(gè)多變量、強(qiáng)耦合的非線性系統(tǒng).在實(shí)際生產(chǎn)過程的各項(xiàng)數(shù)據(jù)中,比表面積作為微粉細(xì)度的指標(biāo),是衡量產(chǎn)品質(zhì)量的重要指標(biāo).磨內(nèi)壓差對于正常生產(chǎn)過程的穩(wěn)定運(yùn)行具有重要意義.本文將微粉的比表面積和磨內(nèi)壓差作為控制量,將喂料量、選粉機(jī)轉(zhuǎn)速、入磨熱風(fēng)溫度及入磨循環(huán)風(fēng)閥開度作為控制變量,通過RNN進(jìn)行模型辨識.
為了在保證產(chǎn)品質(zhì)量的同時(shí),維持生產(chǎn)過程的穩(wěn)定,各控制變量必須達(dá)到某一指定范圍,同時(shí)根據(jù)各執(zhí)行機(jī)構(gòu)自身約束和現(xiàn)場工程師經(jīng)驗(yàn),各控制變量都有其容許的變化范圍,如表2所示.
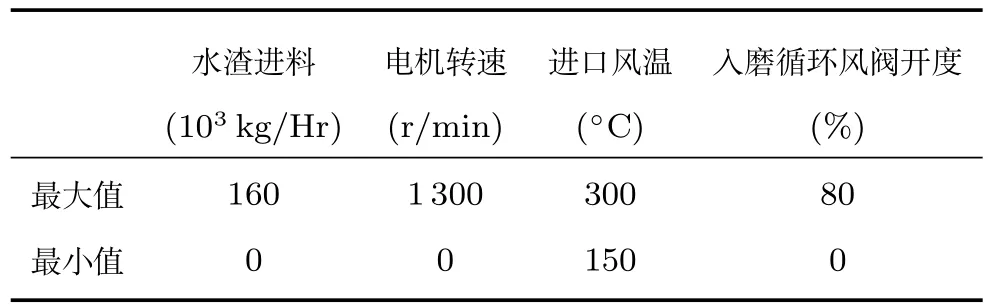
表2 各控制變量容許變化范圍Table 2 Tolerance range of different variables
3.2模型辨識效果
采用如式(5)的遞歸神經(jīng)網(wǎng)對輸入輸出數(shù)據(jù)進(jìn)行辨識.令遞歸神經(jīng)網(wǎng)初始值為(0)=[0;0],各辨識參數(shù)分別為S=-30I2,η=1.5,Λ1=[1 0.1;0.1 1],Λ2=[1 0.2;0.2 1],Λ3=[1 1 1 0.1;1 1 0.1 1;1 0.1 1 1;0.1 1 1 1],Λ4=0.2,Λ5=0.1.辨識效果和辨識誤差如圖4和圖5所示,為了方便顯示模型辨識效果,圖4僅顯示前40組數(shù)據(jù)模型辨識曲線.從圖5可以看出,由于初始值選擇問題,模型誤差在初始階段較大,但經(jīng)過一段時(shí)間后,模型誤差趨近于0,得到的基于數(shù)據(jù)的模型能夠有效地辨識出真實(shí)系統(tǒng).
得到的辨識模型(10)中各穩(wěn)定參數(shù)為

3.3ADP跟蹤控制效果
根據(jù)現(xiàn)場工程師經(jīng)驗(yàn),微粉比表面積維持在440m2/kg左右時(shí),產(chǎn)品質(zhì)量滿足要求,且產(chǎn)量最優(yōu);磨內(nèi)壓差維持在27mbar左右時(shí),保證出入磨物料達(dá)到動態(tài)平衡,生產(chǎn)能夠穩(wěn)定運(yùn)行.基于以上經(jīng)驗(yàn)數(shù)據(jù),通過歸一化,得到微粉生產(chǎn)過程的跟蹤目標(biāo),使輸出狀態(tài)跟蹤到如下期望軌跡:

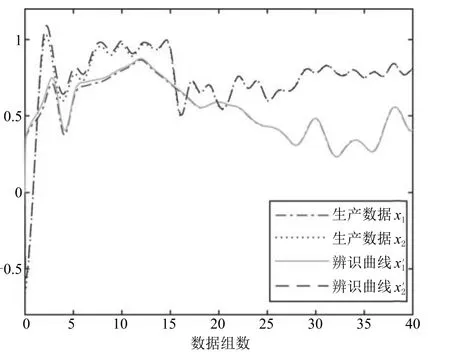
圖4 模型辨識曲線Fig.4 Curve of model identification
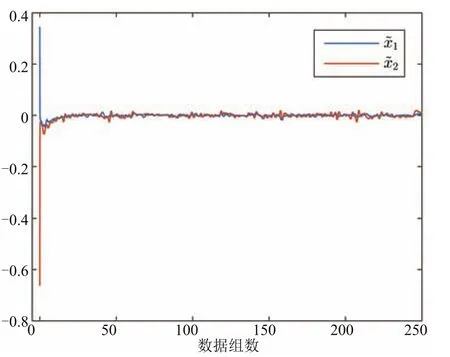
圖5 模型辨識誤差曲線Fig.5 Curve of model identification error
同時(shí)各控制變量需滿足表2所示的控制約束.根據(jù)式(12),可以推導(dǎo)出期望狀態(tài)ud,其變化范圍為

為了使最優(yōu)控制量滿足約束條件,令|ue|≤[1.86 0.59 1.24 1.27]T.
采用帶有控制約束的最優(yōu)跟蹤控制策略,評價(jià)網(wǎng)和執(zhí)行網(wǎng)權(quán)值曲線如圖6和圖7所示,各權(quán)值均收斂到穩(wěn)定值.圖8顯示了期望控制曲線ud和采用本文方法得到的各控制曲線u.采用無控制量約束最優(yōu)控制方法得到的各控制量曲線如圖9所示.圖10顯示了兩種控制方法得到的狀態(tài)跟蹤曲線xc,xu和期望狀態(tài)曲線xd.
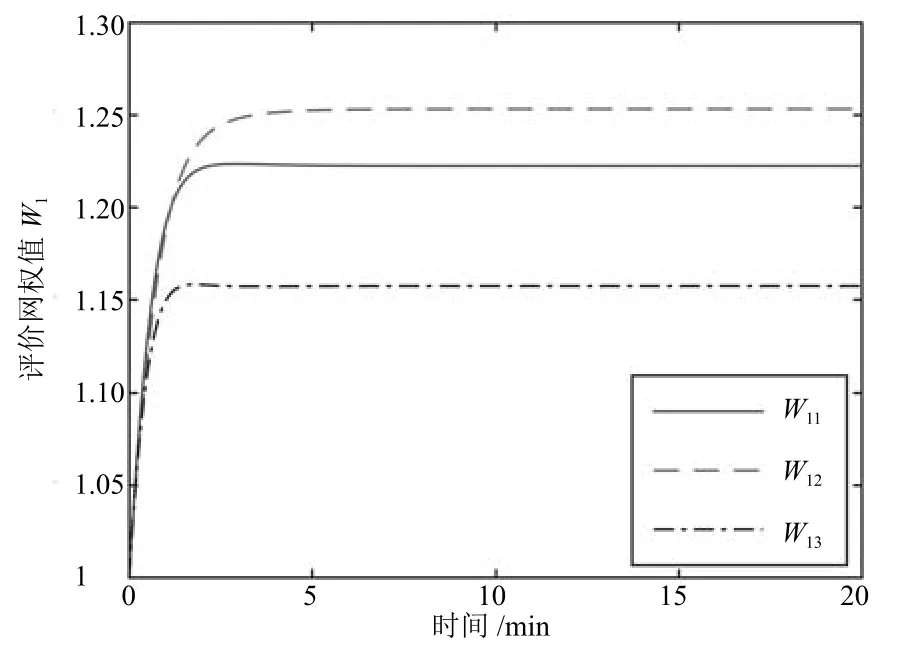
圖6 評價(jià)網(wǎng)權(quán)值曲線Fig.6 Critic network weights
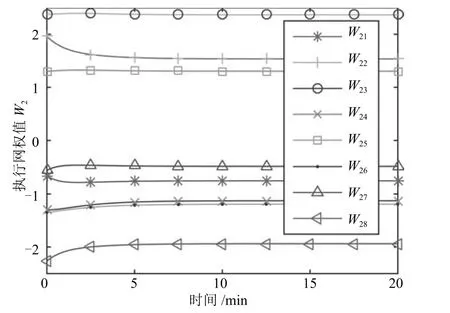
圖7 執(zhí)行網(wǎng)權(quán)值曲線Fig.7 Actor network weights
由圖8及對比表2所示的容許范圍可知,采用本文控制方法能夠使控制誤差ue滿足約束條件,從而保證控制量u始終保持在約束范圍內(nèi).而無約束的最優(yōu)控制由于ue最大值過大,造成控制量u超出約束范圍,如圖9所示.電機(jī)轉(zhuǎn)速u2在初始階段為負(fù)值,明顯與實(shí)際意義不符;進(jìn)口風(fēng)溫u3最大值遠(yuǎn)遠(yuǎn)超過了實(shí)際生產(chǎn)能夠提供的最大風(fēng)溫.因此,圖9所示的無約束控制結(jié)果僅能在理論上跟蹤上期望軌跡,實(shí)際生產(chǎn)過程中很難被采用.同時(shí),如圖10所示,在控制過程中,帶有控制約束的輸出狀態(tài)xc同樣能夠使比表面積跟蹤上期望值440m2/kg,磨內(nèi)壓差穩(wěn)定在27mbar.同時(shí),由于控制量受約束,跟蹤曲線xc超調(diào)量小于無約束最優(yōu)控制曲線xu,但跟蹤上期望軌跡需要更多的調(diào)整時(shí)間.
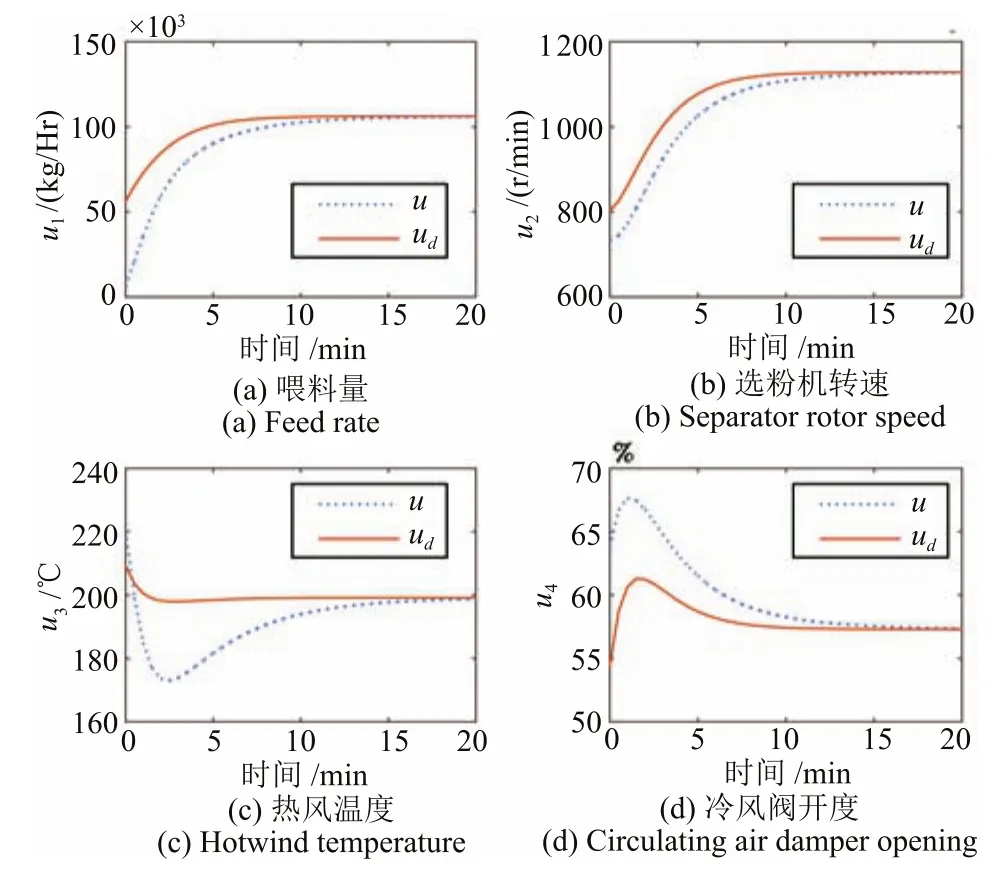
圖8 受約束控制曲線Fig.8 Constrained control signal
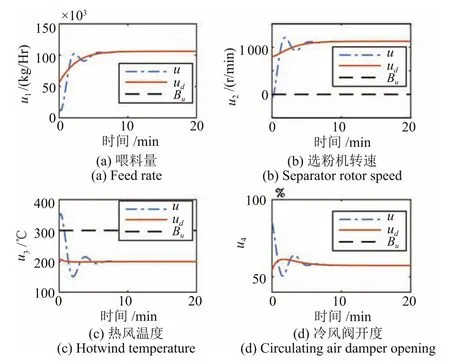
圖9 無約束控制曲線Fig.9 Control signal without constraints
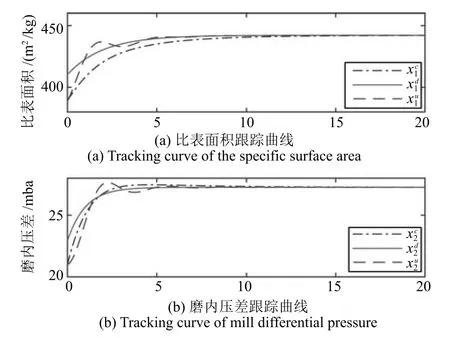
圖10 狀態(tài)輸出曲線Fig.10 Output state signal
4 結(jié)論
針對礦渣微粉生產(chǎn)這一多變量、強(qiáng)耦合、控制有界的復(fù)雜非線性系統(tǒng),本文提出了一種基于數(shù)據(jù)的最優(yōu)跟蹤控制方法.采用遞歸神經(jīng)網(wǎng)建立了生產(chǎn)過程的數(shù)據(jù)驅(qū)動模型,并在該模型的基礎(chǔ)上設(shè)計(jì)了基于近似動態(tài)規(guī)劃的最優(yōu)控制器,在狀態(tài)輸出跟蹤上期望軌跡的同時(shí),保證了控制量始終在約束范圍內(nèi)變化.微粉生產(chǎn)過程的實(shí)驗(yàn)表明,在各執(zhí)行器滿足約束的前提下,該方法能夠保證微粉質(zhì)量和磨內(nèi)壓差穩(wěn)定,從而保證生產(chǎn)過程平穩(wěn)運(yùn)行.在接下來的研究中,將引入微粉產(chǎn)量這一重要指標(biāo),針對產(chǎn)量-質(zhì)量這兩個(gè)互相矛盾的目標(biāo),采用多目標(biāo)優(yōu)化算法求得最優(yōu)解,作為微粉生產(chǎn)過程的跟蹤值,進(jìn)而采用本文方法實(shí)現(xiàn)微粉生產(chǎn)過程產(chǎn)量-質(zhì)量的最優(yōu)跟蹤控制.
References
1 I?s?kda?g,Top?cu˙I B.The effect of ground granulated blastfurnace slag on properties of Horasan mortar.Construction and Building Materials,2013,40:448-454
2 Zhang Y J,Zhang X.Grey correlation analysis between strength of slag cement and particle fractions of slag powder. Cement and Concrete Composites,2007,29(6):498-504
3 Chen Yuan.Study on Separator of Large-scale Vertical Mill[Master dissertation],Chongqing University,China,2008.(陳遠(yuǎn).大型立磨選粉機(jī)研究[碩士學(xué)位論文],重慶大學(xué),中國,2008.)
4 Xu J X,Hou Z S.Notes on data-driven system approaches. Acta Automatica Sinica,2009,35(6):668-675
5 Hou Zhong-Sheng,Xu Jian-Xin.On data-driven control theory:the state of the art and perspective.Acta Automatica Sinica,2009,35(6):650-667(侯忠生,許建新.數(shù)據(jù)驅(qū)動控制理論及方法的回顧和展望.自動化學(xué)報(bào),2009,35(6):650-667)
6 Dai Wei,Chai Tian-You.Data-driven optimal operational control of complex grinding processes.Acta Automatica Sinica,2014,40(9):2005-2014(代偉,柴天佑.數(shù)據(jù)驅(qū)動的復(fù)雜磨礦過程運(yùn)行優(yōu)化控制方法.自動化學(xué)報(bào),2014,40(9):2005-2014)
7 Yan Wen-Jun,Qin Wei.Modeling and control optimization in cement vertical roller mill process.Control Engineering of China,2012,19(6):929-943(顏文俊,秦偉.水泥立磨流程的建模和控制優(yōu)化.控制工程,2012,19(6):929-943)
8 Cai X Y,Meng Q J,Luan W L.Soft sensor of vertical mill material layer based on LS-SVM.In:Proceedings of the2013 International Conference on Measurement,Information,and Control(ICMIC).Harbin,China:IEEE,2013.22 -25
9 Lin X F,Qian Z.Modeling of vertical mill raw meal grinding process and optimal setting of operating parameters based on wavelet neural network.In:Proceedings of the 2014 International Joint Conference on Neural Networks(IJCNN). Beijing,China:IEEE,2014.3015-3020
11 Zhang Hua-Guang,Zhang Xin,Luo Yan-Hong,Yang Jun. An overview of research on adaptive dynamic programming. Acta Automatica Sinica,2013,39(4):303-311(張化光,張欣,羅艷紅,楊王君.自適應(yīng)動態(tài)規(guī)劃綜述.自動化學(xué)報(bào),2013,39(4):303-311)
12 Xu X,Zuo L,Huang Z H.Reinforcement learning algorithms with function approximation:recent advances and applications.Information Sciences,2014,261:1-31
13 Murray J J,Cox C J,Lendaris G G,Saeks R.Adaptive dynamic programming.IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2002,32(2):140-153
14 Wei Q L,Liu D R,Yang X.Infinite horizon self-learning optimal control of nonaffine discrete-time nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems,2015,26(4):866-879
15 Liu D R,Wei Q L.Policy iteration adaptive dynamic programming algorithm for discrete-time nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems,2014,25(3):621-634
16 Zhang H,Cui L,Zhang X,Luo Y H.Data-driven robust approximate optimal tracking control for unknown general nonlinear systems using adaptive dynamic programming method.IEEE Transactions on Neural Networks,2011,22(12):2226-2236
17 Modares H,Lewis F L,Naghibi-Sistani M B.Integral reinforcement learning and experience replay for adaptive optimal control of partially-unknown constrained-input continuous-time systems.Automatica,2014,50(1):193-202
18 Wei Q,Liu D.A novel iterative θ-adaptive dynamic programming for discrete-time nonlinear systems.IEEE Transactions on Automation Science and Engineering,2014,11(4):1176-1190
19 Qin C B,Zhang H G,Luo Y H.Adaptive optimal control for nonlinear discrete-time systems.In:Proceedings of the 2013 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning.Singapore:IEEE,2013.13-18

王 康北京科技大學(xué)自動化學(xué)院博士研究生.2012年獲得北京科技大學(xué)自動化系學(xué)士學(xué)位.主要研究方向?yàn)樽顑?yōu)控制,自適應(yīng)控制.
E-mail:wangkangustb@gmail.com
(WANG KangPh.D.candidate at the School of Automation and Electrical Engineering,University of Science and Technology Beijing.He received his bachelor degree from University of Science and Technology Beijing in 2012. His research interest covers optimal control and adaptive control.)

李曉理北京工業(yè)大學(xué)電子信息與控制工程學(xué)院教授.1997年獲得大連理工大學(xué)控制理論與工程碩士學(xué)位,2000年獲得東北大學(xué)博士學(xué)位.主要研究方向?yàn)槎嗄P妥赃m應(yīng)控制,神經(jīng)網(wǎng)絡(luò)控制.本文通信作者.
E-mail:lixiaolibjut@bjut.edu.cn
(LI Xiao-LiProfessor at the College of Electronic Information and Control Engineering,Beijing University of Technology.He received his master degree in control theory and control engineering from Dalian University of Technology in 1997,and Ph.D.degree from Northeastern University in 2000,respectively.His research interest covers multiple model adaptive control and neural network control.Corresponding author of this paper.)

賈 超北京科技大學(xué)自動化學(xué)院博士研究生.2011年獲得青島理工大學(xué)學(xué)士學(xué)位.主要研究方向?yàn)槎嗄P涂刂疲:刂坪蜕窠?jīng)網(wǎng)絡(luò)控制.
E-mail:jiachaocharles@outlook.com
(JIA ChaoPh.D.candidate at the School of Automation and Electrical Engineering,University of Science and Technology Beijing.He received his bachelor degree from Qingdao Technological University in 2011.His research interest covers multiple model control,fuzzy control,and neural network control.)

宋桂芝濟(jì)南魯新新型建材股份有限公司電氣工程師.2007年獲得山東大學(xué)電氣工程及其自動化碩士學(xué)位.主要研究方向?yàn)榇笮土⒛ハ到y(tǒng)的自動控制.
E-mail:luxinsonggz@163.com
(SONG Gui-ZhiElectrical engineer at Jinan Luxin Materials Company Limited.She received her bachelor degree in electric engineering and automation from Shandong University in 2007.Her research interest covers automatic control of large scale vertical mill.)
Optimal Tracking Control for Slag Grinding Process Based on Adaptive Dynamic Programming
WANG Kang1LI Xiao-Li2JIA Chao1SONG Gui-Zhi3
Super fine slag powder is a new kind of green environmental-friendly construction material,which can greatly improve the mechanical properties of cement concrete.However,the slag powder grinding process is hard to identify by a mechanism model.In this paper,a data-driven based recurrent neural network model is constructed utilizing the information measured from slag grinding system.Based on this model,an adaptive dynamic programming algorithm is proposed to realize the optimal tracking control with constrained control input.Further,this algorithm is applied to the slag grinding process.Simulation examples show that the data-based model can effectively identify the grinding process,and the control method can realize the optimal tracking control of specific surface area and mill differential pressure with control constraints.
Slag grinding process,data driven,adaptive dynamic programming,optimal tracking control,input constrained
Manuscript November 30,2015;accepted March 2,2016
10.16383/j.aas.2016.c150808
Wang Kang,Li Xiao-Li,Jia Chao,Song Gui-Zhi.Optimal tracking control for slag grinding process based on adaptive dynamic programming.Acta Automatica Sinica,2016,42(10):1542-1551
2015-11-30錄用日期2016-03-02
國家自然科學(xué)基金(61473034,61673053),高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金(20130006110008),北京工業(yè)大學(xué)內(nèi)涵發(fā)展-引進(jìn)人才科研啟動經(jīng)費(fèi),北京科技新星計(jì)劃跨學(xué)科合作項(xiàng)目資助
Supported by National Natural Science Foundation of China(61473034,61673053),Specialized Research Fund for the Doctoral Program of Higher Education(20130006110008),Beijing University of Technology Start-up Funding of Content Development and the Introduced Talent Research,and Beijing Nova Programme Interdisciplinary Cooperation Project
本文責(zé)任編委魏慶來
Recommended by Associate Editor WEI Qing-Lai
1.北京科技大學(xué)自動化學(xué)院 北京1000832.北京工業(yè)大學(xué)電子信息與控制工程學(xué)院北京1001243.濟(jì)南魯新新型建材股份有限公司濟(jì)南250109
1.School of Automation and Electrical Engineering,University of Science and Technology Beijing,Beijing 1000832.College of Electronic Information and Control Engineering,Beijing University of Technology,Beijing 1001243.Jinan Luxin Materials Company Limited,Jinan 250109

