粒子群優化算法的性能分析和參數選擇

王東風　孟麗

粒子群優化算法的性能分析和參數選擇

王東風1孟麗1

慣性權重和加速因子是影響粒子群算法優化性能的重要參數.基于常用的12個測試函數，本文通過實驗研究了不同參數組合下粒子的探索能力和算法的優化性能，在此基礎上推薦了一組固定的參數組合.通過慣性權重和加速因子的不同變化策略組合對算法性能影響的實驗分析，推薦了一種變化的參數設置方法.基于CEC2015發布的15個基準函數進一步驗證了本文推薦的參數選取方法的有效性.最后討論了粒子群優化（Particle swarm optimization，PSO）算法在連續優化和離散優化方面的應用問題.

粒子群優化，探索能力，算法性能，參數選取

引用格式王東風，孟麗.粒子群優化算法的性能分析和參數選擇.自動化學報，2016，42（10）:1552-1561

粒子群優化（Particle swarm optimization，PSO）算法是Kennedy和Eberhart在1995年提出的一種群智能優化算法［1］，源于對鳥群捕食行為的研究.1998年，Shi等［2］在原始PSO中引入了慣性權重，后來被稱為標準PSO.由于PSO結構簡單、易于實現，且不需要借助問題的特征信息，已受到眾多學者的關注，在算法的性能改進和分析方面不斷取得新的成果［3-4］，在多個領域得到廣泛應用［5］.

在PSO算法中，有一些需要調節的參數：種群規模（種群的個體數目）N，速度限值位置限值慣性權重w，加速因子c1和c2.其中，w，c1和c2對算法性能的影響較大，目前有很多學者對其設定和調節方式進行了研究.在參數選取方面，文獻［6-9］通過實驗或理論分析，推薦了一組固定參數值.在時變參數的調節方面，對于慣性權重的調整，文獻［2，10］提出了隨迭代次數減小慣性權重，文獻［11-12］給出了隨機慣性權重策略，文獻［13-15］根據種群的信息自適應地調節慣性權重；對于加速因子的調整，文獻［16］提出在迭代的過程中，c1和c2線性遞減，文獻［17］則提出c1線性遞減、c2線性遞增，文獻［18］基于個體的更新信息給出了一種c1和c2的自適應調整策略.以上這些參數的調整方法，都在一定程度上提高了算法的性能，但是，當涉及到時變參數時，并沒有考慮到慣性權重和加速因子之間的配合作用.單獨依靠調整慣性權重或加速因子，并不能在種群的局部開發能力（Exploitation ability）和全局探索能力（Exploration ability）之間進行平衡.事實上，各個參數之間需要相互配合，才能夠達到預定的效果.本文考慮了各個參數之間的配合，基于在感興趣的參數范圍內進行的優化測試實驗數據，通過定義最優解超越次數，推薦了一組固定和時變的參數值.

本文其余部分安排如下：第1節先給出標準粒子群算法的形式；第2節通過仿真實驗研究不同參數對粒子探索能力、算法成功率和算法性能的影響，推薦一組固定參數值；第3節研究算法中的認知參數c1和社會參數c2的變化策略對算法性能的影響，并推薦一組變參數的組合設定方式；第4節基于CEC2015發布的15個基準函數進一步驗證本文推薦的參數選取方法的有效性；第5節討論PSO算法在連續優化和離散優化方面的應用問題；第6節對全文進行了總結.

1　標準粒子群（SPSO）算法

在粒子群算法中，每個粒子代表尋優空間中一個潛在的解，有一個由被優化的函數決定的適應值.在每一次迭代進化中，粒子通過自身和群體的歷史最優位置更新當前的速度和位置.在任意t+1時刻，粒子群算法中第i個粒子第d維的速度和位置更新公式為

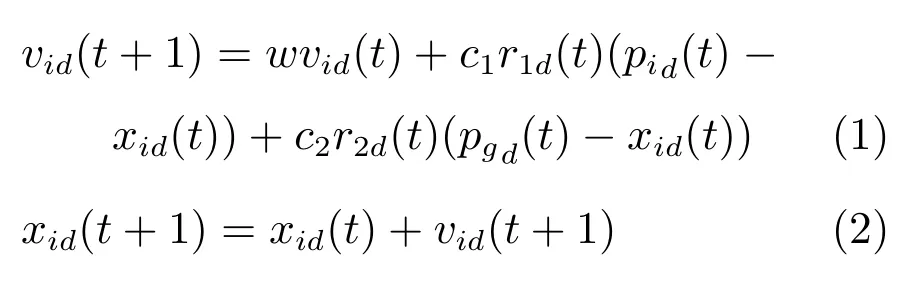
其中，vid和xid分別為粒子的速度和位置，w為慣性權值，c1和c2稱為加速因子，分別為認知參數和社會參數，pid和pgd分別為個體和群體的歷史最優位置，r1d和r2d為兩個相互獨立的服從［0，1］之間均勻分布的隨機數，正是這兩個隨機數的引入，使得算法的進化過程具有一定的不確定性，也因此賦予了算法一定的空間探索能力，從而有利于找到問題的最優解.

2　粒子群算法的性能分析

下面通過實驗說明粒子的探索能力和算法的性能與參數之間的關系.我們感興趣的參數區域是w∈［-1，1］，c1+c2∈［0，8］，這也是絕大多數文獻研究的區域.所有的實驗都基于以下12個常用的基準函數，由于這些基準函數被普遍應用，在此只給出函數的名稱，即：Fun1：Sphere；Fun2：Rosenbrock；Fun3：Schwefel′s P2.21；Fun4：Schwefel′s P2.22；Fun5：Schwefel′s P1.2；Fun6：Rastrigin；Fun7：Griewank；Fun8：Ackley；Fun9：Schwefel；Fun10：Weierstrass；Fun11：Penalized1；Fun12：Penalized2.

2.1參數對粒子探索能力的影響

粒子群算法參數w，c1，c2的選取對算法的優化性能有很大影響.不同的參數組合下，粒子的軌跡形式是不同的，決定了粒子探索能力的大小.在種群進化過程中的第t代，若粒子能夠找到比t-1代的全局最優解更好的解，那么則認為粒子具有一定的探索能力.我們通過以下實驗觀察不同的參數對粒子探索能力的影響.設種群規模為N，為每個粒子設置不同的參數，設置變量Pnumi記錄具有不同參數的粒子i在進化的過程中超越上一代的全局最優解的次數：

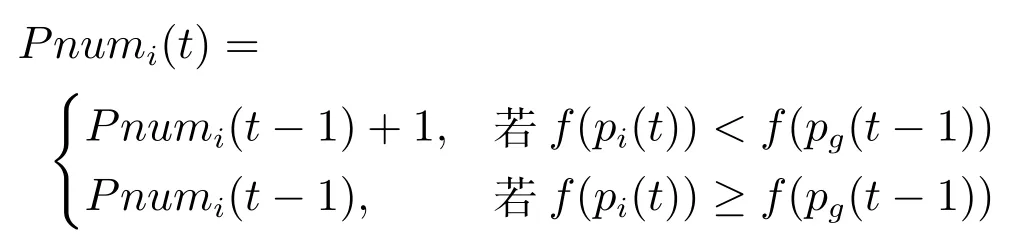
其中，t=2，3，···，tmax.

將上面定義的Pnumi稱為粒子i的第t代最優解超越次數，它表征了粒子探索能力的大小.顯然，探索能力大的粒子更有可能找到全局最優解.

對于所有的粒子設置相同參數的粒子群算法，則所有的粒子在統計意義上具有相同的探索能力；隨著算法進化進程的推進，具有不同的狀態的粒子在當前迭代步則具有不同的探索能力；被設置不同參數的粒子，一般則具有不同的探索能力.這已得到作者們進行的大量仿真優化計算實例的證實.圖1為4組不同的PSO種群在優化函數Sphere時每個粒子的Pnum值：種群大小均為50，函數設置為10維，最大迭代次數為500，每組種群運行50次，記錄每個粒子Pnum值的平均值.圖1（a）為種群中粒子設置為相同的參數時（w=0.6，c1=c2=1.7）每個粒子的Pnum值；圖1（b）、圖1（c）和圖1（d）為種群中粒子設置不同參數時每個粒子的Pnum值，其中圖1（b）中，第1～50個粒子的w值均為0.6，c1=c2為0.04：0.04：2；圖1（c）中，第1～50個粒子的w值均為1.7，c1=c2分別為0.02：0.02：1，圖1（d）中，第1～10個粒子的w值均為0.2，c1=c2分別為0.2：0.2：2，第11～20個粒子的w均為0.4，c1=c2分別為0.2：0.2：2，依此類推，第41～50個粒子的w均為1.0，c1=c2分別為0.2：0.2：2.

在w∈［-1，1］，c1+c2∈［0，8］的參數區域上對所用的12個基準函數進行蒙特卡羅實驗.每個函數進行兩組實驗：1）種群中的個體取相同的w，c1=c2則取不同的數值.本組實驗中，根據種群參數w的值分為51組子實驗，w的取值按0.04的間隔從-1～1，每個子實驗中，種群大小均為81，c1=c2按0.05的間隔從0～4取81個值分配給不同的粒子，函數運行50次，記錄不同粒子在50次運行中的Pnum的平均值.2）種群中的個體取不同的w，而c1=c2取相同的固定值.本組實驗中，根據種群參數c1（c2）的值分為81組子實驗，c1=c2的取值按0.05的間隔從0～4，每個子實驗中，種群大小均為51，w按0.04的間隔從-1～1共取51個值分配給不同的粒子，函數運行50次，記錄不同粒子在50次運行中的Pnum的平均值.將兩組實驗中得到的相同參數組合下粒子i的Pnumi進行求和，得到此參數組合在不同種群環境中的綜合探索性能，進而得到整個參數區域內不同參數組合的綜合超越次數.相比于超越次數的絕對值，我們更關心不同參數組合下粒子探索能力的相對關系，因此對每個函數得到的結果分別進行歸一化處理，結果如圖2所示.值得注意的是，在6＜c1+c2≤8的區域中，對于任意的w運行結果Pnumi均為0，因此，6＜c1+c2≤8的區域并未在圖中進行展示.從圖2可以明顯地看到粒子群算法的參數取值對不同基準函數的優化性能的共性和特性，即對每個基準函數來說，算法的探索能力對參數的取值表現出明顯的區域性，總體來說大同小異，這為PSO的參數選擇提供了很好的指導作用.

2.2參數對算法成功率的影響

在w∈［-1，1］，c1+c2∈［0，8］矩形域上按照等間隔的網格取點，（c1+c2）軸取點間隔為0.02，共101點，w軸取點間隔為0.04，共201點，共可得到20301組不同的參數組合.對每一組參數組合進行蒙特卡羅仿真實驗，優化12個基準函數.種群規模N為50，最大迭代次數tmax為500，每個函數獨立運行50次.為每個函數設置尋優精度goal，記錄不同參數組合下達到所設置尋優精度的成功率，繪制成灰度圖像.每個函數的尋優精度為圖中的goal所示，是通過實驗測試得到的，原則是不會使測試結果得到的最佳參數組合區域過大而失去指導意義，也不會使其過小而失去一般性參考價值.設置一定的尋優精度，實驗結果如圖3所示.

由圖3可以看到，除了Fun2、Fun6、Fun7和Fun9，其他8個函數的最優參數區域在形狀上非常相似，并且都出現在靠近過渡區域的邊界部分.這一部分的參數使得粒子軌跡能夠以一定的幅值振蕩，使得探索能力和開發能力獲得很好的平衡.對于Fun2、Fun6、Fun7和Fun9這4個函數，Fun2為很難極小化的典型病態二次函數；Fun6、Fun7為典型的具有大量局部最優點的復雜多峰函數；Fun9的全局最優點與第2最優點相距很遠，算法往往朝著錯誤的方向（第2最優點）收斂.這4個函數只靠調節算法參數很難得到滿意的解，運行結果的規律性沒有其他函數那么明顯.

將圖2與圖3對比可以看到，圖2和圖3并不是完全對應的.圖2中展示的粒子的探索能力為粒子的局部探索能力和全局探索能力的總和，而不同的函數具有不同的特性，對群體的局部探索能力和全局探索能力的要求是不同的.雖然總的探索能力與尋優性能并不是完全對應的，但是，沒有探索能力的參數區域，基本上是不可取的.

2.3幾種典型參數選取策略的性能對比及一組固定參數推薦值

由圖3可以看到，使得算法獲得優良性能的參數區域因函數的不同而有一些差異，基本上沒有一組參數能夠使得所有的函數同時獲得最優，尤其可以看到，Fun2和Fun9的較優參數區域的交集部分是非常小的.盡管如此，仍然可以選擇出一些參數，使算法在所有函數上獲得比較令人滿意的綜合性能.為了能夠更加容易地選擇出在12個函數上綜合性能較優的參數，我們將不同函數下得到的運行結果進行整合，得到算法在不同參數下的綜合性能的示意圖，見圖4.

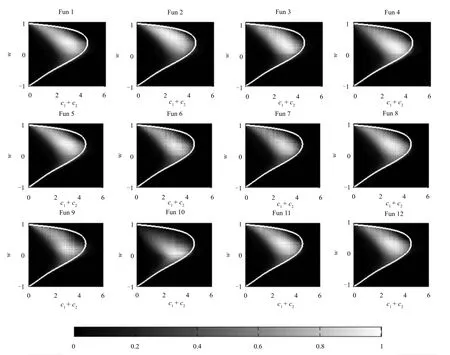
圖2　粒子探索能力與參數的關系Fig.2　Relationship between particle exploration ability and its parameters

圖4中標示的PARA1和PARA2分別為文獻［6］和文獻［7］推薦的參數取值.其中，參數組合PARA1（w=0.7298，c1=c2=1.49618）是Eberhart等［6］將帶有慣性權重和帶有收縮因子的兩種形式的粒子群算法進行比較后推薦的一組參數；參數組合PARA2（w=0.6，c1=c2=1.7）是Trelea［7］在分析粒子軌跡收斂域的基礎上推薦的參數.參數組合PARA3是我們根據性能綜合圖，即圖4推薦的一組參數：w=0.4，c1=c2=2.在另外的工作中，Samal等［8］在理論分析的基礎上給出了一組具有較快收斂速度的參數：w=0.6，c1r1=0.103，c2r2=2.897（參數組合PARA4）；Carlisle等［9］在文獻［6］的基礎上進行了進一步的實驗，考慮了的情況，通過仿真實驗得到，當時，算法的性能較優，即w=0.7298，c1=2.0434，c2=0.9487（參數組合PARA5）.我們將這5組參數在12個函數上進行測試，種群規模、最大迭代次數和每個函數獨立運行的次數都與第2.2節一致.記錄運行數次結果中的最小值（min）、最大值（max）、平均值±標準差（mean ±std），以及優化成功率（Success rate，SR），并且記錄了不同參數在每個函數指定尋優精度下的成功率，結果列于表1中.為了清晰地顯示參數對算法性能的影響，此處為12個函數指定的尋優精度依次為：10-20，3，10-5，10-10，10-20，5，10-1，10-10，500，10-3，10-20，10-20.以下各測試試驗中所用的尋優精度均與此相同.首先來看參數PARA1～PARA3的運行結果，這三個參數組合基本上都在圖4中的較優區域里.三組參數在Fun1，Fun3，Fun4，Fun8，Fun11和Fun12上的運行結果差別不大.在Fun2，Fun5，Fun6，Fun7，Fun9和Fun10上的差別相對較大，參數PARA1在Fun2，Fun7上表現較優，在Fun5上表現較差；參數PARA2在Fun6，Fun9上表現較差；參數PARA3在Fun6，Fun9和Fun10上表現較優，在Fun2，Fun7上表現較差.正如從圖3中看到的，每組參數都有其適應的函數.再來看參數PARA4和參數PARA5，同樣的，每組參數在不同函數上表現出的性能也是有差別的.參數PARA4的綜合性能在所有的參數中是比較差的.參數PARA5是在參數PARA1的基礎上發展而來的，保持c1與c2之和不變，改變c1和c2的比例，除了在Fun2上，參數PARA5的性能要優于參數PARA1.

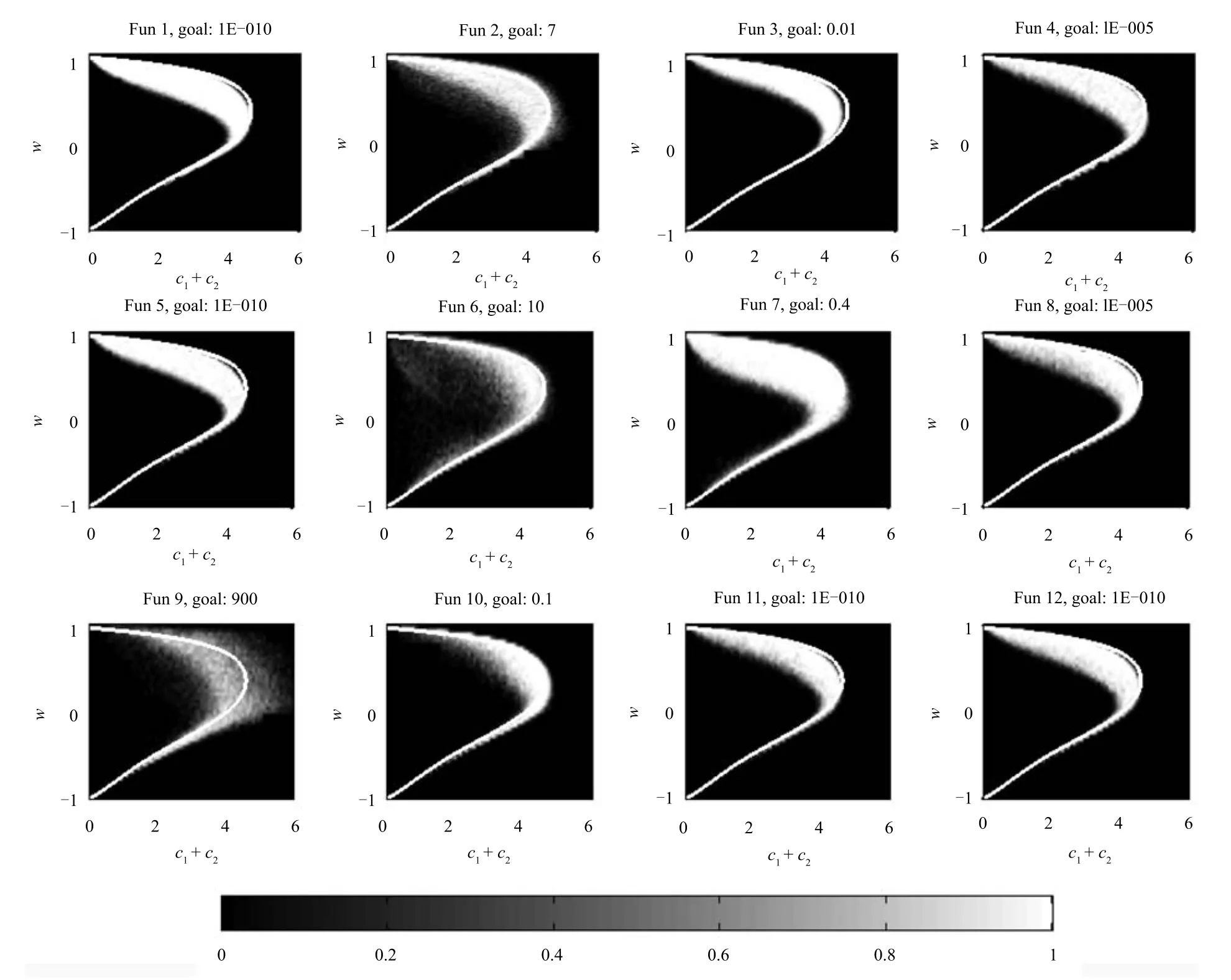
圖3　算法成功率與參數的關系Fig.3　Relationship between the algorithm success rate and particle parameters

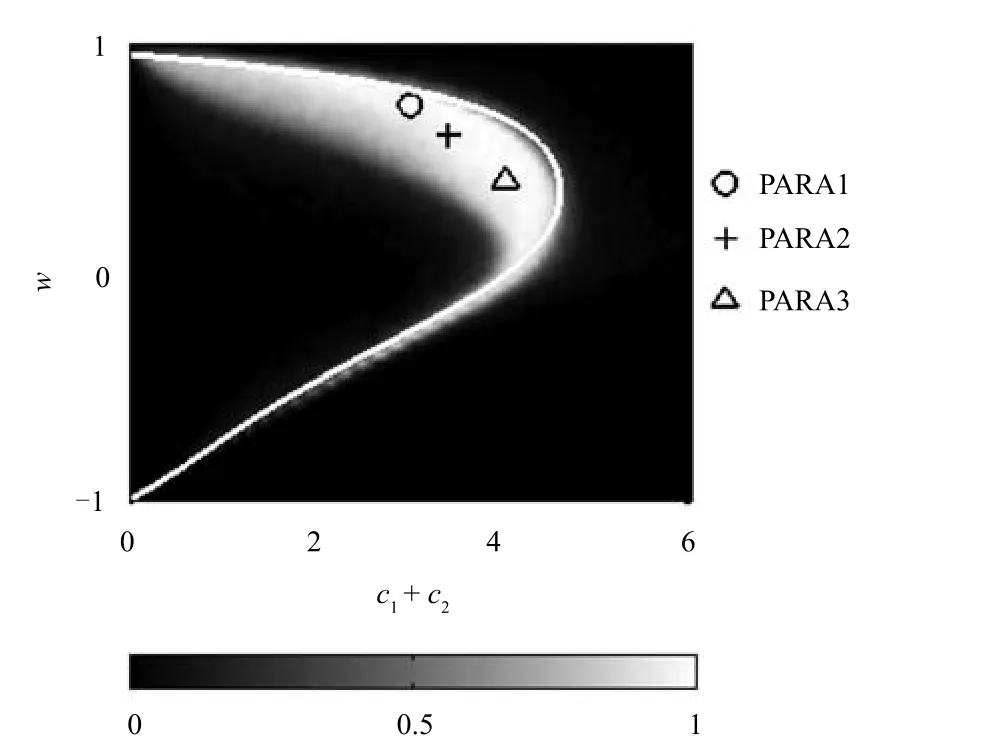
圖4　算法在12個測試函數上的性能總和Fig.4　Total optimization performance on the 12 test functions

為了能夠比較全面地了解c1和c2的比例對算法的影響，我們保持參數PARA1中的w=0.7298，c1+c2=2.992，將c1在c1+c2的總和中所占的比率由0逐漸增加到1，在12個函數上的運行結果如圖5所示.Fun2，Fun6，Fun7和Fun9在整個比率范圍內的變化情況較為復雜，圖5（a）為這4個函數的變化情況，另外8個函數的優化情況展示在圖5（b）中.當c1在c1與c2之和中所占比例c1/（c1+c2）在0.6～0.8之間時，圖5（b）中的8個函數都獲得了很好的性能，而圖5（a）中，算法在Fun6，Fun7和Fun9上的成功率隨c1/（c1+c2）的增加而增大，在0.8附近到達最好值；Fun2則相反，成功率隨著c1/（c1+c2）的增加而減小，在0.8時的成功率非常低.當c1/（c1+c2）取為0.683時，便可得到參數組合PARA5，對于圖5（b）的8個函數來說，是最好的選擇.而對于圖5（a）的4個函數來說，是綜合考慮的折中選擇.

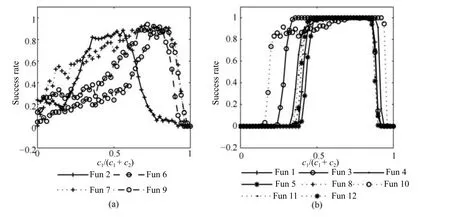
圖5　c1所占比率對算法成功率的影響Fig.5　The influence of ratio c1on algorithm′s success rate

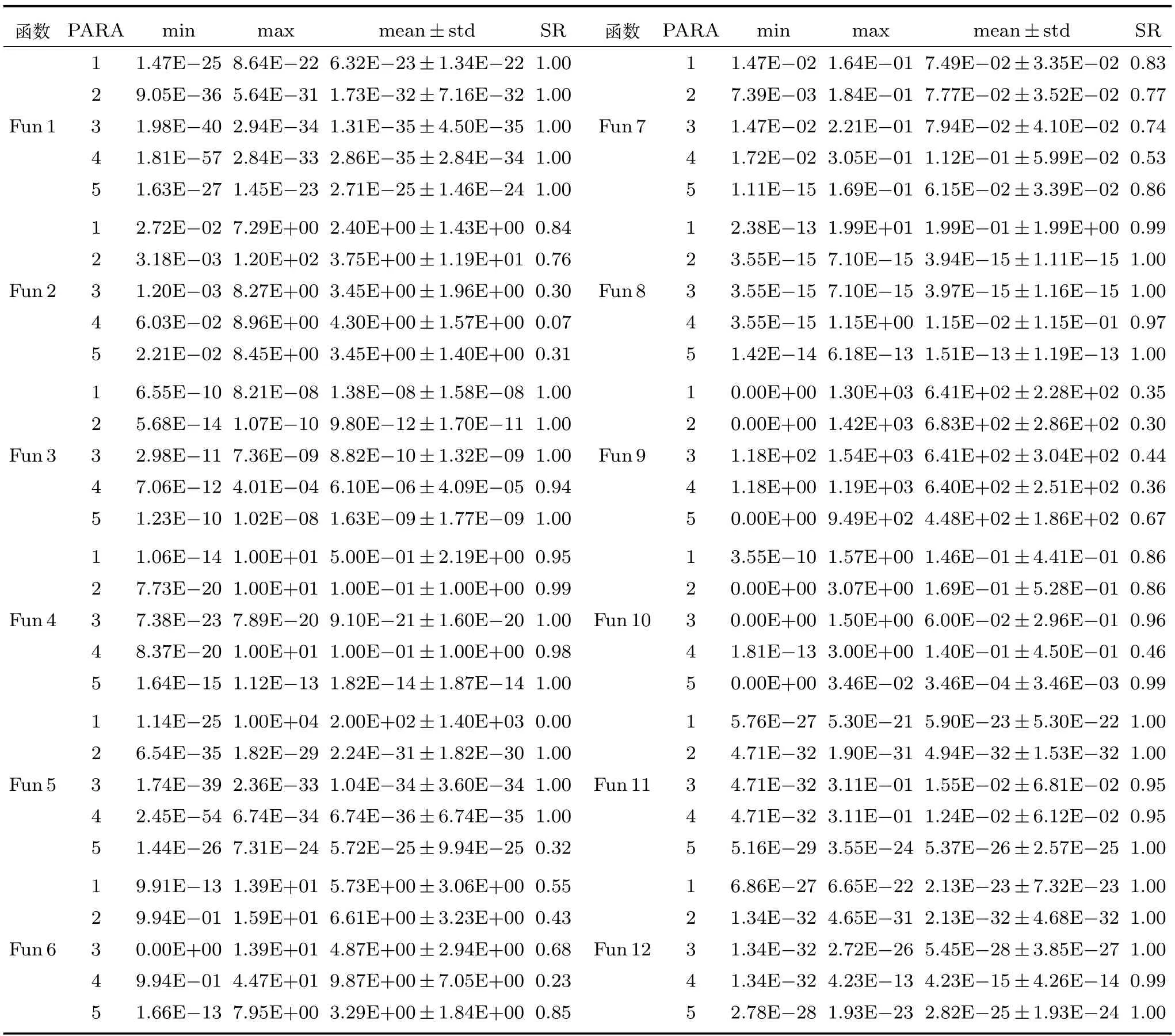
表1　5組參數的運行結果對比Table 1　Comparison of running results on 5 parameters

3　幾種典型參數變化策略的性能對比及一種變化參數推薦值

以上的實驗和討論都是基于在種群進化過程中c1和c2為定值的情形下進行的，從表1和圖5的運行結果可以看到，無論c1和c2是否相等，采用c1和c2定值的調節算法在算法性能上是有局限性的.為了進一步提高算法的性能，下面觀察在迭代的過程中c1和c2按照不同的方式變化時對算法性能的影響.實驗仍然基于12個測試函數，對于固定的w，c1和c2有9種不同的調整策略，為簡潔表示，引入3個符號：“→”表示參數c1或c2保持不變，為1.5；“↑”表示參數c1或c2在迭代的過程中線性地由0.5上升到2.5；“↓”表示參數c1或c2在迭代的過程中線性地由2.5下降到0.5.則c1和c2的9種調節策略表示為：

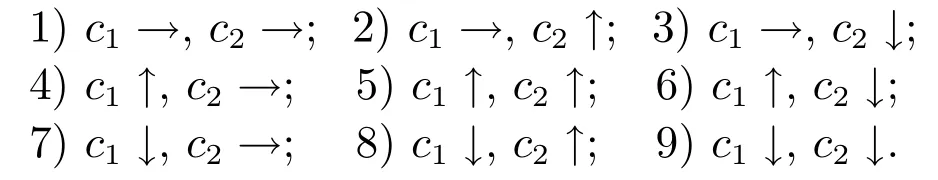
對于每個函數，進行如下實驗：w從0逐漸增加到1，對于每個w的值，分別用以上9種策略進行實驗.每個優化實驗運行50次.記錄最終結果到達指定精度的成功率.運行結果如圖6所示，縱軸為算法尋優的成功率，橫軸為w值，每個子圖中的9條曲線，分別對應上述c1和c2的9種取值策略.

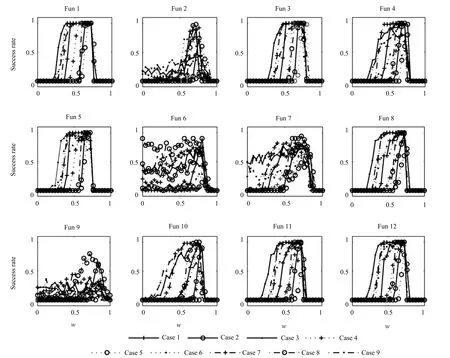
圖6　變化的c1和c2取值策略對算法成功率的影響Fig.6　The influence of varying c1and c2on algorithm′s success rate

由圖6可以看到，每一種c1和c2的取值策略都有與其對應的w的最佳取值范圍.除了Fun2，Fun6，Fun7和Fun9，各種策略的性能隨著w的變化情況是類似的，即：沿著w軸的正方向，w的整個區間可以分為5個區域：1）初始階段，成功率幾乎為0；2）緊隨其后的很小的區域內，成功率由0迅速上升達到曲線的最大值；3）在一段區域內，成功率保持為最大值；4）緊隨其后的很小的區域內，成功率迅速下降；5）最后區域，成功率幾乎為零.區域1和區域3的大小與參數的取值策略緊密相關.而所有的策略在w＞0.68時，成功率幾乎均為0.區域3正是我們需要的部分.在這8個函數上，策略3、策略7和策略9使得區域3較為寬廣.再來看Fun6，Fun7和Fun9，策略2取得了最好的成功率，其次為策略8.在Fun6和Fun7上，對于某些c1和c2的取值策略，w的取值可以比較小，也能夠使算法獲得不錯的性能.在Fun2上，各個策略相適應的w值范圍都很小.相比較而言，不論是從w的適用范圍的大小還是從成功率的高低來看，策略4、策略5和策略6都是不可取的，即增大的調節方式總是不可取的.綜合12個測試函數來看，策略8在Fun6，Fun7和Fun9上，在w=0.68時具有很突出的效果，并且，在其他8個函數上，雖然策略8的w的適用范圍并不寬廣，但在w=0.68時，恰恰都具有很好的性能，因此，w=0.68，c1在迭代過程中由2.5線性減小到0.5，c2由0.5線性增加到2.5，是一種很好的參數設置方式.這與Ratnaweera等［17］提出的c1遞減和c2遞增的調整策略是相符的，在文獻［17］中，c1和c2的變化范圍與本文相同，而w的取值由0.9隨迭代線性減小到0.4.本文提出的和文獻［17］中的參數設置方法在12個函數上的運行結果如表2所示.在表2中，Method-ours指本文推薦的w=0.68，c1在迭代過程中由2.5線性減小到0.5，c2由0.5線性增加到2.5.Method-［17］是指文獻［17］給出的w的取值由0.9隨迭代線性減小到0.4，c1和c2的變化范圍與Method-ours相同.由表2的運行結果可以看到，本文的參數設置方法要優于文獻［17］中的方法.值得注意的是，c1和c2的變化范圍，與使其獲得較優性能的w也是相互配合的，在我們的實驗中發現，當變化范圍為［0.5，2.05］時，w取0.75的性能要優于0.68.因此，3個參數之間的相互配合是非常重要的.

表2　本文與文獻［17］參數設置的優化結果比較Table 2　Comparison of optimization results between the parameters set in this paper and［17］

4　本文參數設置方式優化性能的進一步驗證

為進一步驗證本文參數設置方法的有效性，將第2節的一組固定參數推薦值和第3節的時變參數設置方式，應用于2015年的進化計算世界大會，即CEC2015發布的15個基準函數［19］.

對于參數優化能力的驗證，種群大小與前面所有試驗設置相同（設置為50），函數維數為10，最大迭代次數為5000，每個函數運行次數為100.試驗僅記錄達到指定精度的成功率（Success rate，SR），其中，F1～F15的指定精度分別為：3000，1500，20，10，500，1000，10，200，110，1000，500，110，30，3000，110.

對圖4給出的3種典型固定參數，即文獻［6］和文獻［7］推薦的參數取值PARA1和PARA2，以及本文的參數推薦取值PARA3，表3給出了應用于CEC2015的15個基準函數上運行結果的對比.可以看出，本文的參數推薦值PARA3在15個函數上的表現略優于PARA1和PARA2.

對第3節推薦的時變參數設置方式和文獻［17］的參數設置方式，表4給出了應用于CEC2015的15個基準函數上運行結果的對比.可以看出，本文推薦的時變參數設置方式在15個函數上的表現優于文獻［17］的參數設置方式.

5　本文推薦的PSO參數應用于連續優化問題和離散優化問題的討論

PSO算法最初是針對連續優化問題提出的，相關研究也主要集中在連續函數優化方面［20-22］，即第1節描述的標準算法被廣泛研究和應用.本文研究的出發點也主要是針對連續優化問題，文中給出的12個標準測試函數和CEC2015發布的15個基準函數［19］的優化測試，驗證了本文方法在連續優化問題上的有效性.

表3　本文給出的固定參數推薦值在CEC2015基準函數F1～F15上的運行結果Table 3　Running results on CEC2015 Benchmark functions F1～F15 with fixed parameters

表4　本文給出的時變參數設置方式在CEC2015基準函數F1～F15上的運行結果Table 4　Running results on CEC2015 Benchmark functions F1～F15 with time-varying parameters

對于離散優化（或組合優化）問題而言，解空間是離散點的集合，而非連續區域，因此利用PSO算法解決離散優化問題，一般需要修正位置和速度更新公式，或者對問題進行變形，這方面的工作大致可分為如下三類［21-22］：1）直接將連續PSO用于離散優化問題的求解；2）將速度作為位置變化的概率；3）重新定義PSO算法的操作算子.對于前兩種情形，本文推薦的參數取值方法仍然適用，因為算法在本質上依然遵從標準的PSO連續問題求解規則.但對于第三種情形，一般都是針對要求解的具體問題，定義不同的PSO操作算子，使得PSO算法在形式上與標準PSO算法差別較大，從而本文推薦的參數取值方法難以保證其優化效果，這方面的問題有待進一步研究.

6　結論

粒子群算法的可調參數共同影響著算法的優化性能，本文將研究重點放在了慣性權重w和加速因子c1，c2的設定和調節上.基于12個常用的、不同類型的基準函數，在w∈［-1，1］，c1+c2∈［0，8］的參數區域內進行了全面的仿真研究.通過實驗結果可以看到，常常被提到的“慣性權重起著調節種群全局搜索能力和局部搜索能力”的說法是欠全面的，種群的搜索能力和算法的性能，是依靠w，c1和c2的相互配合來調節的，并不是僅靠一個參數可以決定的.在對固定參數的情形進行仿真并給出參數推薦值后，還研究了時變參數對算法的影響，給出了一種推薦的時變參數設置方法.最后通過CEC2015發布的15個基準函數進一步驗證了本文推薦的參數選取方法的有效性，并討論了PSO算法在連續優化問題和離散優化問題方面的應用.

References

1 Kennedy J，Eberhart R.Particle swarm optimization.In: Proceedings of the 1995 IEEE International Conference on Neural Networks.Perth，Australia:IEEE，1995.1942-1948

2 Shi Y，Eberhart R.A modified particle swarm optimizer. In:Proceedings of the 1998 IEEE International Conference on Evolutionary Computation.Anchorage，AK，USA:IEEE，1998.69-73

3 Zhang Yong，Gong Dun-Wei，Zhang Wan-Qiu.A simplex method based improved particle swarm optimization and analysis on its global convergence.Acta Automatica Sinica，2009，35（3）:289-298（張勇，鞏敦衛，張婉秋.一種基于單純形法的改進微粒群優化算法及其收斂性分析.自動化學報，2009，35（3）:289-298）

4 Pan Feng，Zhou Qian，Li Wei-Xing，Gao Qi.Analysis of standard particle swarm optimization algorithm based on Markov chain.Acta Automatica Sinica，2013，39（4）:381-389（潘峰，周倩，李位星，高琪.標準粒子群優化算法的馬爾科夫鏈分析.自動化學報，2013，39（4）:381-389）

5 Liu Zhao-Hua，Zhou Shao-Wu，Liu Kan，Zhang Jing.Permanent magnet synchronous motor multiple parameter identification and temperature monitoring based on binary-modal adaptive wavelet particle swarm optimization.Acta Automatica Sinica，2013，39（12）:2121-2130（劉朝華，周少武，劉侃，章兢.基于雙模態自適應小波粒子群的永磁同步電機多參數識別與溫度監測方法.自動化學報，2013，39（12）: 2121-2130）

6 Eberhart R C，Shi Y.Comparing inertia weights and constriction factors in particle swarm optimization.In:Proceedings of the 2000 Congress on Evolutionary Computation.La Jolla，CA:IEEE，2000.84-88

7 Trelea I C.The particle swarm optimization algorithm:convergence analysis and parameter selection.Information Processing Letters，2003，85（6）:317-325

8 Samal N R，Konar A，Das S，Abraham A.A closed loop stability analysis and parameter selection of the particle swarm optimization dynamics for faster convergence.In:Proceedings of the 2007 IEEE Congress on Evolutionary Computation.Singapore:IEEE，2007.1769-1776

9 Carlisle A，Dozier G.An off-the-shelf PSO.In:Proceedings of the 2001 Workshop on Particle Swarm Optimization.Indianapolis，USA，2001.1-6

10 Hu Jian-Xiu，Zeng Jian-Chao.Selection on inertia weight of particle swarm optimization.Computer Engineering，2007，33（11）:193-195（胡建秀，曾建潮.微粒群算法中慣性權重的調整策略.計算機工程，2007，33（11）:193-195）

11 Yan Li-Ping，Zeng Jian-Chao.Particle swarm optimization with self-adaptive stochastic inertia weight.Computer Engineering and Design，2006，27（24）:4677-4679，4706（延麗平，曾建潮.具有自適應隨機慣性權重的PSO算法.計算機工程與設計，2006，27（24）:4677-4679，4706）

12 Chalermchaiarbha S，Ongsakul W.Stochastic weight tradeoff particle swarm optimization for nonconvex economic dispatch.Energy Conversion and Management，2013，70:66-75

13 Ao Yong-Cai，Shi Yi-Bing，Zhang Wei，Li Yan-Jun.Improved particle swarm optimization with adaptive inertia weight.Journal of University of Electronic Science and Technology of China，2014，43（6）:874-880（敖永才，師奕兵，張偉，李焱駿.自適應慣性權重的改進粒子群算法.電子科技大學學報，2014，43（6）:874-880）

14 Zhan Z H，Zhang J，Li Y，Chung H S H.Adaptive particle swarm optimization.IEEE Transactions on Systems，Man，and Cybernetics，Part B（Cybernetics），2009，39（6）:1362-1381

15 Alfi A.PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems. Acta Automatica Sinica，2011，37（5）:541-549

16 Suganthan P N.Particle swarm optimiser with neighbourhood operator.In:Proceedings of the 1999 Congress on Evolutionary Computation.Washington DC，USA:IEEE，1999.1958-1962

17 Ratnaweera A，Halgamuge S K，Watson H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients.IEEE Transactions on Evolutionary Computation，2004，8（3）:240-255

18 Yamaguchi T，Yasuda K.Adaptive particle swarm optimization:self-coordinating mechanism with updating information.In:Proceedings of the 2006 IEEE International Conference on Systems，Man，and Cybernetics.Taipei，China: IEEE，2006.2303-2308

19 Liang J J，Qu B Y，Suganthan P N，Chen Q.Problem Definitions and Evaluation Criteria for the CEC 2015 Competition on Learning-based Real-parameter Single Objective Optimization.Technical Report 201411A，Computational Intelligence Laboratory，Zhengzhou University，Zhengzhou China，and Technical Report，Nanyang Technological University，Singapore，2014.

20 Cui Zhi-Hua，Zeng Jian-Chao.Particle Swarm Optimization.Beijing:Science Press，2011.（崔志華，曾建潮.微粒群優化算法.北京:科學出版社，2011.）

21 Wang Ling，Liu Bo.Particle Swarm Optimization and Scheduling Algorithms.Beijing:Tsinghua University Press，2008.（王凌，劉波.微粒群優化與調度算法.北京:清華大學出版社，2008.）

22 Guo Wen-Zhong，Chen Guo-Long.Discrete Particle Swarm Optimization Algorithm and Its Application.Beijing:Tsinghua University Press，2012.（郭文忠，陳國龍.離散粒子群優化算法及其應用.北京:清華大學出版社，2012.）

王東風博士，華北電力大學控制與計算機工程學院教授.主要研究方向為群智能優化算法和智能控制.

E-mail:wangdongfeng@ncepu.edu.cn

（WANG Dong-FengPh.D.，professor at the School of Control and Computer Engineering，North China Electric Power University.His research interest covers swarm intelligence-based optimization and intelligent control.）

孟 麗華北電力大學控制與計算機工程學院博士研究生.主要研究方向為智能優化算法及其應用.本文通信作者.

E-mail:mengli2014@163.com

（MENG LiPh.D.candidate at the School of Control and Computer Engineering，North China Electric Power University.Her research interest covers swarm intelligence-based optimization and its application. Corresponding author of this paper.）

Performance Analysis and Parameter Selection of PSO Algorithms

WANG Dong-Feng1MENG Li1

Inertia weight and acceleration factors have significant impact on the performance of particle swarm optimization（PSO）algorithm.Through simulation experiments on twelve classical benchmark functions，this paper studies the algorithm′s exploitation ability and optimization performance with different parameters.Based on the experimental results，we recommend a setting for fixed parameters.Furthermore，we study the situation where inertia weight remains unchanged and acceleration factors change with iterations.Then a setting for varying parameters is recommended.The recommended parameters setting methods are verified through 15 benchmark functions that were published in CEC2015. At the end of the paper，a discussion of the PSO application issue on continuous optimization problems and discrete optimization problems is given.

Particle swarm optimization（PSO），exploitation ability，optimization performance，parameter selection

Manuscript November 18，2015；accepted March 26，2016

10.16383/j.aas.2016.c150774

Wang Dong-Feng，Meng Li.Performance analysis and parameter selection of PSO algorithms.Acta Automatica Sinica，2016，42（10）:1552-1561

2015-11-18錄用日期2016-03-26

國家自然科學基金（61203041），教育部高等學校博士學科點專項科研基金（20120036120013），中央高校基本科研基金（20140139）資助

Supported by National Natural Science Foundation of China（61203041），Specialized Research Fund for the Doctoral Program of Higher Education（20120036120013），and the Fundamental Research Funds for the Central Universities（20140139）

本文責任編委董海榮

Recommended by Associate Editor DONG Hai-Rong

1.華北電力大學自動化系保定071003

1.Department of Automation，North China Electric Power University，Baoding 071003