雙M-Z光纖干涉儀中隨機生成數偏振控制算法

黃微衛，張志勇，邵理陽

（西南交通大學信息光子與通信研究中心，成都 610031）

光纖光纜技術與應用

雙M-Z光纖干涉儀中隨機生成數偏振控制算法

黃微衛，張志勇，邵理陽

（西南交通大學信息光子與通信研究中心，成都 610031）

采用基于兩路檢測信號相關系數的隨機生成數算法，通過偏振控制器對輸入偏振態進行調節，解決了雙M-Z（馬赫-曾德）光纖傳感系統中出現的偏振相位偏移問題，改善了兩路檢測信號的相關性。對隨機生成數算法的可行性及其3個重要參數進行了分析討論。實驗結果表明，算法執行5min可搜索到邦加球的絕大部分區域，具備全局搜索能力，并且通過合理地設置隨機生成數算法的參數，可使系統在3min左右搜索到偏振態的最佳位置，使兩路檢測信號的相關系數保持在0.9左右，恢復兩路檢測信號的良好相關性。

雙馬赫-曾德干涉儀；相關系數；隨機生成數算法；偏振控制

0 引 言

隨著人們安全防范意識的提高，一些重要的設施及場所的安全防護成為首要解決的問題。光纖傳感系統憑借其優良的特性，成為周界防護領域的研究熱點。本課題研究的是基于雙M-Z（馬赫-曾德）光纖干涉儀的周界防護系統，該方法將兩路檢測信號的相關性良好作為前提條件［1］，系統通過計算兩路信號的互相關峰值所對應的位置來確定時延的大小，從而實現系統的定位。然而，在實際使用中，系統的敷設環境、光纖的偏振特性等會使系統產生偏振相位偏移問題，影響兩路檢測信號的相關性，導致系統的定位精度下降甚至無法定位［1］。為了提高系統的定位精度，必須通過調節系統的偏振態來消除偏振相位偏移的影響，保證兩路檢測信號的良好相關性［2］。

利用偏振控制器并結合偏振控制算法對偏振態進行調節是最常用的方法［2］。常見的偏振控制算法有模擬退火算法、遺傳算法和粒子群算法等，這些算法復雜度較高，需要復位算法，控制速度和效率都有限，更有甚者容易陷入局部最優而難以搜索到最佳偏振態位置［3］。本文提出一種以兩路檢測信號的相關系數作為反饋控制量的隨機生成數算法，通過調節偏振控制器改變輸入光的偏振態，來搜索系統最佳偏振態的位置。

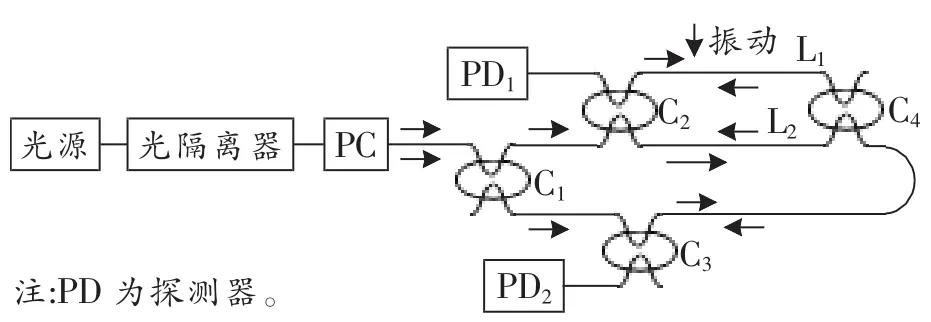
圖1 雙M-Z光纖干涉儀系統結構示意圖

1 系統的偏振控制模型

圖1為雙M-Z光纖干涉儀系統結構示意圖。光源輸出的光信號經光隔離器和PC（偏振控制器）后被C1耦合器分成順時針和逆時針兩路傳感光信號，圖中PC的作用是對輸入偏振態進行控制。

假設在傳感光路上，傳感臂L1和L2上順時針傳輸的光場表達式分別為E1和E2，逆時針傳輸的光場表達式分別為ET1和ET2，則探測器PD1和PD2接收到的光信號Eout1、Eout2的表達式為［4-5］:

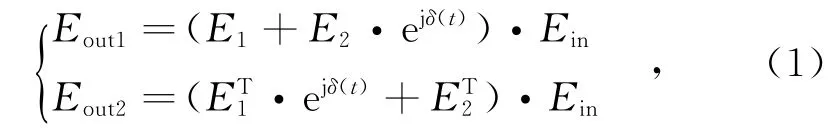
式中，δ（t）為由振動信號引起的兩路信號的相位差。兩路光強信號I1（t）、I2（t）可表示為［5］

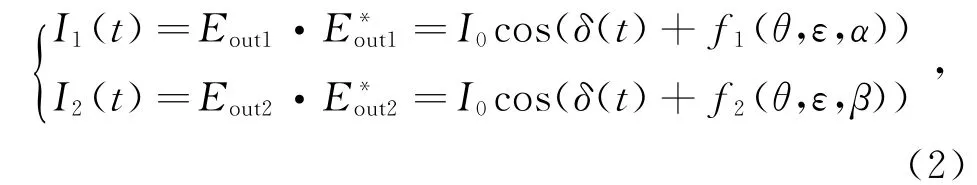
式中，I0為光源輸出光強；θ和ε分別為光源經PC調制后的方位角和橢率角；α和β分別為順時針和逆時針方向光路中的相位偏移；f1（θ，ε，α）和f2（θ，ε，β）為由于相位偏移和PC共同作用產生的附加相位差。為了研究附加相位對互相關函數的影響，兩路檢測信號的互相關系數表達式如下［5］:

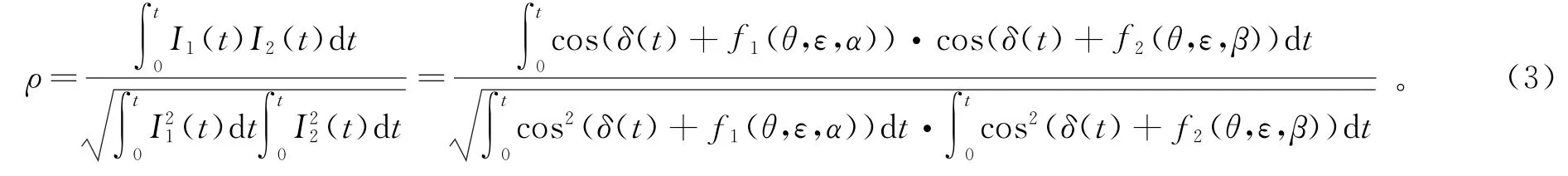
通過式（3）可以看出，相關系數ρ主要由兩路信號的相位決定，通過改變附加相位差f1（θ，ε，α）和f2（θ，ε，β），可使兩路檢測信號的相關性發生變化。附加相位差是由偏振相位偏移和PC共同決定的，其中偏振相位偏移由輸入偏振態、光纖的雙折射特性和系統的應用環境決定，后兩項無法人為改變，而輸入偏振態可由PC改變［6］。因此，本文結合PC和隨機生成數算法搜索與當前光纖偏振特性匹配的輸入偏振態，以改善信號的相關性［7］。

2 隨機生成數算法可行性分析

由上文可知，偏振相位偏移引起的偏振態的改變具有隨機性:光源輸出偏振態未知，系統環境未知，光纖的雙折射特性也不確定。因此，為了使系統的偏振態達到良好的狀態，對偏振控制算法的要求是:（1）具備全局搜索的能力，能夠遍歷到邦加球的任意一點；（2）跳出局部搜索范圍并最終趨于最優的狀態［8］。

為了驗證隨機生成數算法的全局搜索能力和搜索速度，系統搭建好測試平臺，啟動算法，觀察偏振分析儀中邦加球的掃描軌跡，邦加球是偏振光形象表示，球上的每個點都代表偏振態的一種狀態。實驗記錄了不同時刻下算法執行5min時邦加球的搜索軌跡，如圖2所示。從圖中可以看出，隨機生成數算法在較短的時間內可以覆蓋邦加球的絕大部分區域。由于隨機生成數產生新解不會依賴之前的解，因此它不會陷入局部搜索狀態，具有全局搜索的能力。同時在算法中加入了自動調節閾值和啟動算法閾值，加快了算法的收斂速度，保證算法能夠最終趨于全局最優的狀態。

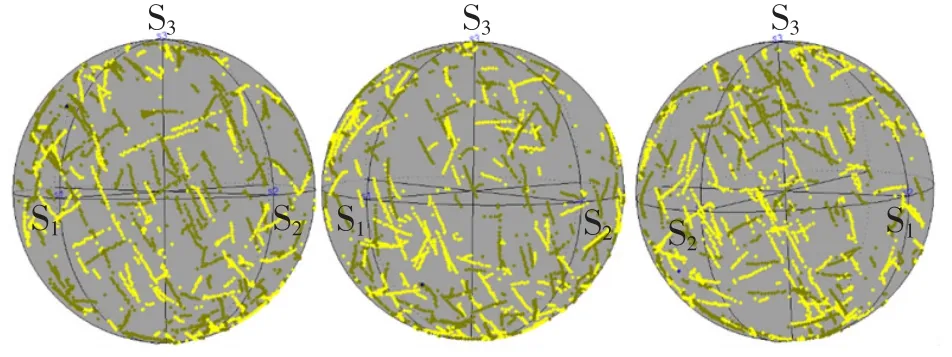
圖2 算法執行5min時邦加球的搜索軌跡圖

3 基于兩路檢測信號相關系數的隨機生成數算法

算法的流程如圖3所示。在算法執行之前，需手動設定相關系數閾值Fth、自動調節閾值Ath和啟動算法閾值n。隨機生成數算法是通過系統隨機生成PC的某個通道和對應該通道的數字電壓值，系統采集兩路檢測信號并計算其相關系數f（x1，x2），將f（x1，x2）與設定的Fth進行比較，根據比較結果確定是否繼續對PC的通道和電壓隨機賦值，再通過設定Ath和n來實現偏振控制的自動調節。

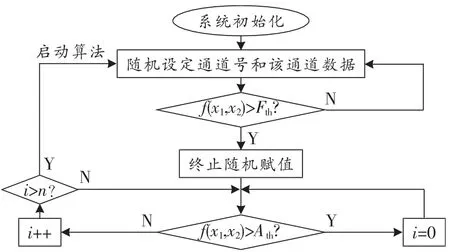
圖3 隨機生成數算法流程圖

4 算法關鍵參數的設定

由上一節可知，隨機生成數算法主要設置3個變量:相關系數閾值Fth、自動調節閾值Ath和啟動算法閾值n。系統每秒鐘執行一次算法，獲取一次相關系數值，在算法的參數討論中，算法執行了250次，采集了250次相關系數值。

4.1 相關系數閾值Fth的設定

Fth的大小關系到算法搜索到偏振態的好壞，如果Fth設置得較低，則算法在還未搜索到最佳偏振態時就會提前終止；如果Fth設置得較高，則算法會一直處于搜索狀態，也不容易得到最佳偏振態。實驗設置了3個Fth值，分別為0.88、0.93和0.97，并分別進行了實驗和比較，結果如圖4所示，此時另外兩個參數分別設定為Ath=0.8和n=5。

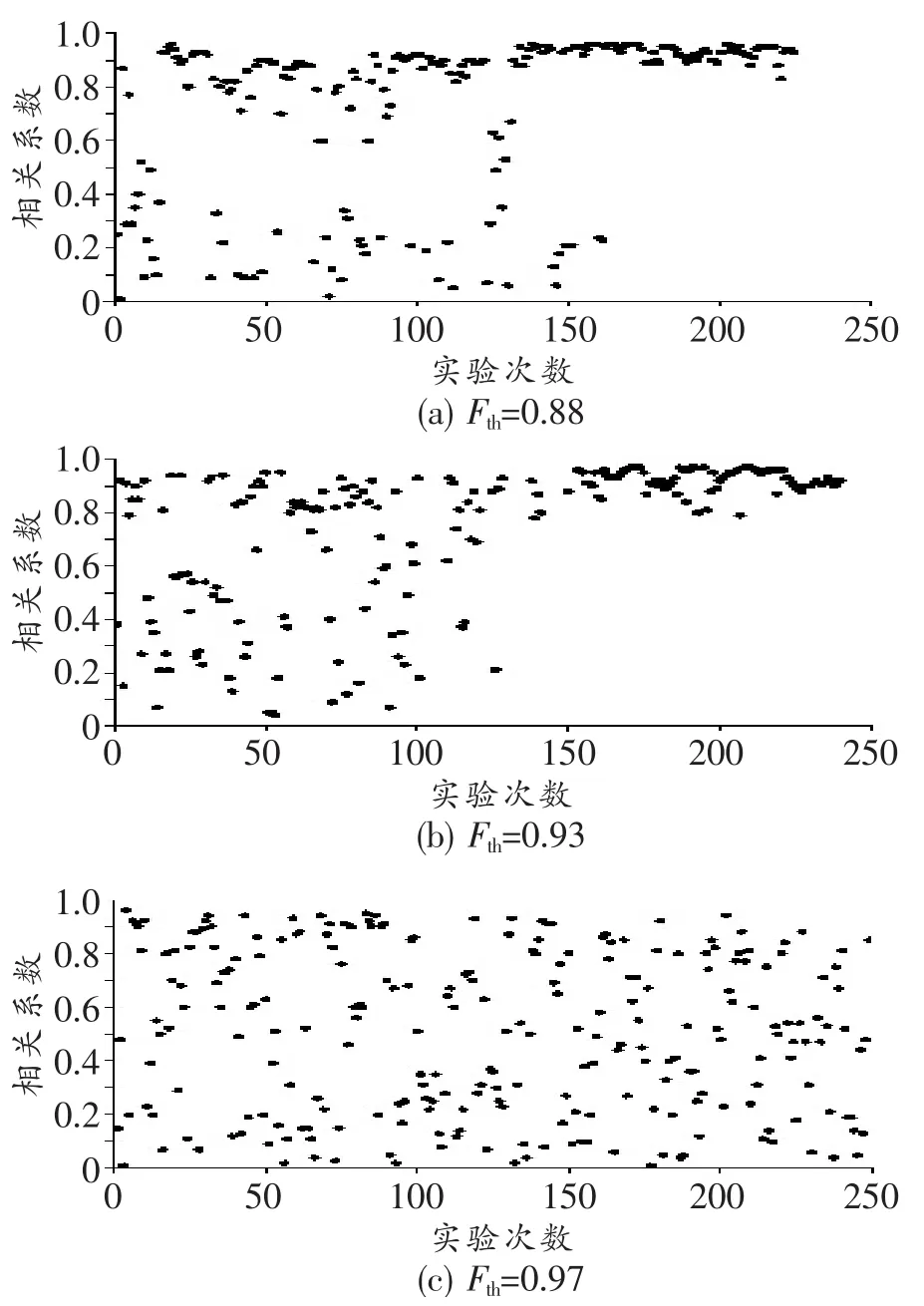
圖4 不同Fth下的相關系數分布圖

由圖可知，當Fth設定為0.88和0.93時，相關系數分布大致相同，即經過前期不斷搜索，最終趨于比較穩定的狀態。當Fth設定為0.97時，由于設置值過高，當算法搜索到一個比較好的狀態時也會被系統誤認為狀態不好，導致算法繼續執行，因此偏振態難以趨于穩定。

4.2 自動調節閾值Ath的設定

Ath是為了檢驗當前相關系數是否保持在一個良好的狀態，通常Ath要比Fth低，但為了保證相關系數保持在良好的狀態，Ath不能設定得太低。實驗設置了3個Ath值:0.75、0.80和0.85，并分別進行了實驗比較，結果如圖5所示，此時另外兩個參數分別設定為Fth=0.93，n=5。

由圖可知，當Ath比較低時，自動調整比較少，系統處于不穩定的狀態，算法不太容易搜索到最佳偏振態工作點。當Ath設定為0.80和0.85時，算法通過前期的搜索比較容易達到接近最佳偏振態工作點的位置，并最終維持在偏振態較好的狀態。

4.3 啟動算法閾值n的設定

啟動算法閾值n表示連續出現相關系數小于Ath的次數。n設定得較小時，可使算法搜索頻率加快，系統在較短的時間容易達到偏振態較好的狀態，但是n設定得過小時，算法在搜索時容易偏離原先搜索到的良好偏振態。n設定得過大，算法收斂過快，不容易趨于最佳偏振態工作點，同時在系統偏振態偏離最佳工作點時，不利于偏振態自動控制。實驗設置了3個n值:3、5和9，并分別進行了實驗比較，結果如圖6所示，此時另外兩個參數分別設定為Fth=0.93，Ath=0.8。由圖6可知，當n值較小時，算法搜索的次數較頻繁，系統能在較短時間達到偏振態較好的狀態，但是不利于穩定到最佳偏振態的位置；當n值較大時，系統的自動控制能力較弱，不易搜索到偏振態最佳工作點。

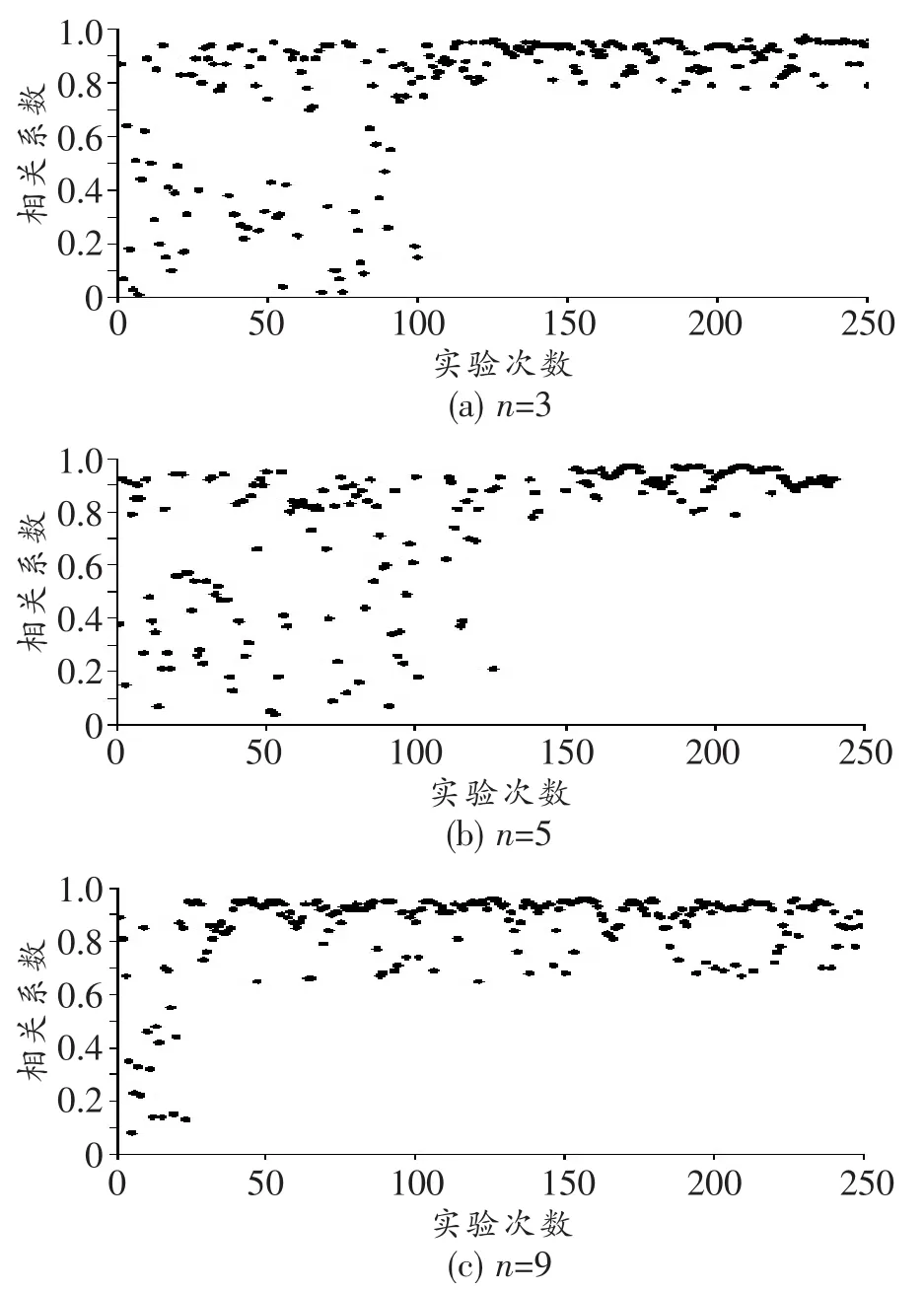
圖6 不同n值下的相關系數分布圖

通過上述的參數討論分析，算法參數的合理設置為Fth=0.93，Ath=0.80，n=5。

5 系統實驗分析

按圖1所示結構，搭建了雙M-Z周界防護實驗裝置。系統初始化設置采樣頻率為10 MHz，采樣數據1 Mbyte。系統采用通用光電公司（General Photonics）的PCD-M02型集成PolaRiteⅡ/ⅢPC，該PC采用4個互成45°的波片結構，可以實現任意偏振態向任意偏振態之間的轉換。

根據上文分析，設置隨機生成數算法參數，分別對系統偏振控制前后的兩路檢測信號進行采集，實驗比較了算法執行前后的300次相關系數的分布情況，如圖7所示。由圖可見，系統在偏振控制前，兩路檢測信號的相關系數處于不規律的變化，相關性極差。執行算法3min后，兩路檢測信號的相關系數基本維持在0.8以上，平均在0.9左右，且保持穩定。實驗表明，以兩路檢測信號的相關系數作為反饋控制量的隨機生成數算法可以有效改善兩路檢測信號的相關性，提高系統的定位精度。

為了進一步說明該算法的優勢，本文與文獻中基于兩路檢測信號相關系數的模擬退火偏振控制算法［5］進行對比，結果發現，使用模擬退火算法時相關系數保持在0.9左右，但是由于模擬退火算法采用了內外循環控制，一次算法歷程需要大約1min，而平均搜索到最佳偏振態位置需要10～20個歷程，耗時較長，而且模擬退火算法容易陷入局部最優狀態而難以搜索到全局最優偏振態位置。

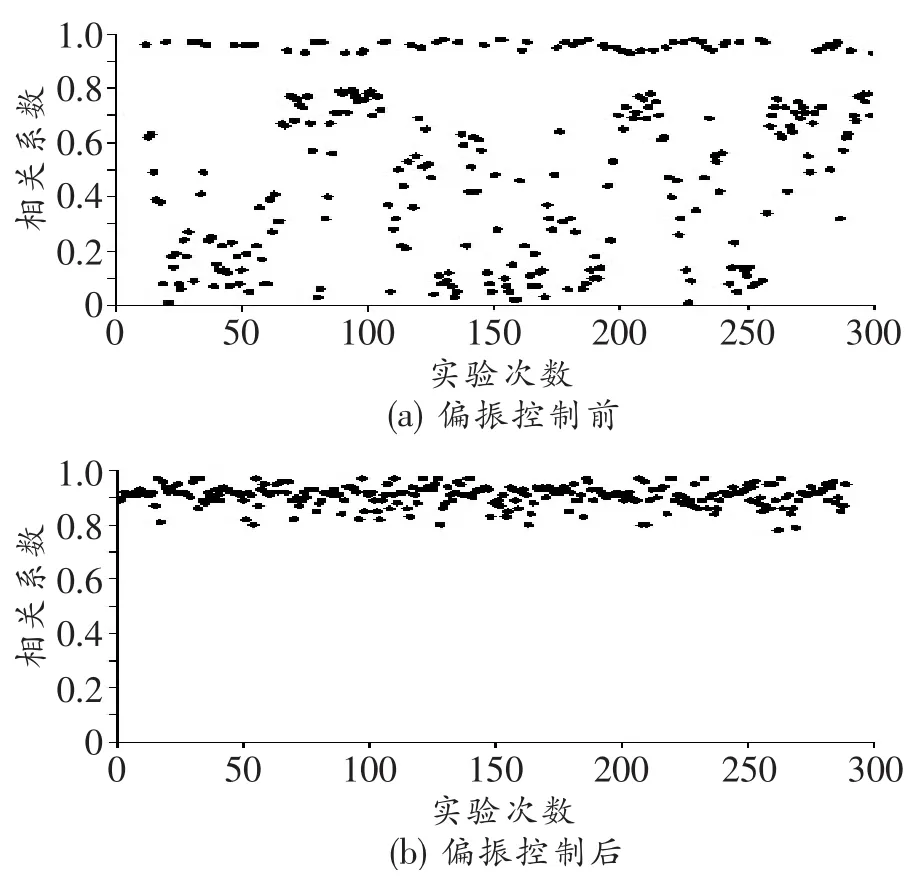
圖7 偏振控制前后的相關系數分布圖

6 結束語

本文提出了基于兩路檢測信號相關系數的隨機生成數偏振控制算法，結合PC對輸入偏振態進行實時控制，有效地消除了系統的偏振相位偏移影響。對隨機生成數算法的3個關鍵參數進行了討論，通過實驗驗證了各個參數對系統相關性的影響，確定了算法參數的最優值。最后，實驗比較了算法執行前后相關系數的分布情況，結果表明，采用隨機生成數偏振控制算法可使系統在3min左右搜索到偏振態的最佳位置，使兩路檢測信號的相關系數保持在0.9左右，兩路檢測信號的相關性良好。

［1］廖俊，張志勇，邵理陽，等.基于FFTW算法的M-Z周界防護系統［J］.光通信研究，2015，（4）:37-38.

［2］靳志剛，曾周末，封皓.雙Mach-Zehnder光纖干涉儀中的遺傳偏振控制算法［J］.半導體光電，2014，35（4）:705-707.

［3］張啟業，朱勇，蘇洋，等.非理想情況下的實時偏振控制算法［J］.激光與光電子學進展，2013，（9）:38-44.

［4］封皓，靳世久，曾周末，等.基于瓊斯矩陣建模的管道泄漏檢測及預警系統的定位誤差分析［J］.光學學報，2009，29（03）:723-727.

［5］張溪默，曾周末，封皓，等.雙Mach-Zehnder光纖干涉儀中的模擬退火偏振控制算法 ［J］.激光與紅外，2012，42（3）:324-330.

［6］Feng Hao，Zhu Lin，Jin Shijiu，et al.Modeling of pipeline leakage detection and prewarning system for location error analysis based on jones matrix［J］.Journal of the Japan Petroleum Institute，2009，52（3）: 114-119.

［7］李永倩，孟祥騰，安琪，等.電光調制器自適應偏振控制系統設計與實現［J］.紅外與激光工程，2015，44（6）:1854-1858.

［8］曾周末，張溪默，封皓，等.雙Mach-Zehnder光纖干涉傳感系統中的偏振衰落控制 ［J］.光學精密工程，2012，20（3）:468-476.

Polarization Manipulation Algorithm for Random Number Generation in Dual Mach-Zehnder Interferometer

HUANG Wei-wei，ZHANG Zhi-yong，SHAO Li-yang
（Center for Information Photonics&Communications，Southwest Jiaotong University，Chengdu 610031，China）

Random number generation algorithm based on correlation between two channels is adopted.The proposed method eliminates the phase shift in dual Mach-Zehnder（M-Z）fiber sensing system through manipulating the polarization of the input，and improves the correlation of the signals.The feasibility of the generation algorithm and three corresponding parameters are theoretically analyzed.The experimental results indicate that most area of the Poincare sphere can be swept in 5min.Meanwhile，the optimal position of the polarization can be searched in 3min.Subsequently，the correlation of the signals is improved with a correlation coefficient of 0.9.

dual M-Z interferometer；correlation coefficient；random number generation algorithm；polarization manipulation

TN911

A

1005-8788（2016）05-0008-04

10.13756/j.gtxyj.2016.05.003

2016-04-15

國家自然科學基金面上項目（61475128）；科技部國際合作專項（2014DFA11170）；中央高校基本科研基金資助項目（2682014RC22）

黃微衛（1992-），男，江西撫州人。碩士研究生，主要研究方向為光纖傳感技術。