含微網的配電系統可靠性評估

張海燕，韓肖清，肖　春，秦亞斌

（1.太原理工大學電氣與動力工程學院，太原 030024；2.中北大學計算機與控制工程學院，太原 030051；3.國網山西省電力公司客戶服務中心，太原 030008；4.國網山西省電力公司檢修公司，太原 030032）

式中：0表示故障；1表示正常運行。

采用兩狀態抽樣法，則風機正常運行臺數為

與逆變器串聯后，光伏-逆變器組的故障率λPV和故障停電時間rPV分別為

含微網的配電系統可靠性評估

張海燕1，2，韓肖清1，肖春3，秦亞斌4

（1.太原理工大學電氣與動力工程學院，太原 030024；2.中北大學計算機與控制工程學院，太原 030051；3.國網山西省電力公司客戶服務中心，太原 030008；4.國網山西省電力公司檢修公司，太原 030032）

分布式電源接入配電系統，使系統的結構和運行方式發生變化，給配電系統的可靠性評估帶來挑戰。本文考慮分布式電源的間歇性、隨機性和風機、光伏系統的故障率，建立了分布式電源的出力模型和負荷的時變模型，引入虛擬等值電源的概念，提出基于序貫蒙特卡洛模擬的含微網配電系統可靠性評估算法，分析微網并入電網后對配電系統各區域可靠性的影響程度。以改進的IEEE RBTS Bus6系統為例，對配電系統各負荷點的可靠性進行評估，驗證了該方法的有效性。

序貫蒙特卡洛法；可靠性評估；虛擬等值電源；微網

隨著世界能源危機、環境問題的加劇，分布式電源的發展得到越來越多的重視。為協調大電網與分布式電源間的矛盾，充分挖掘分布式電源為電網和用戶所帶來的價值和效益，在21世紀初學者們提出了微電網的概念［1］。微網將發電機、負荷、儲能裝置及控制裝置等結合，形成一個單一可控的單元，向用戶供給電能。微網中的電源多為微電源，包括風力發電機、光伏發電以及微型燃氣輪機等。它們接在用戶側，具有低成本、低電壓和低污染等特點。微網既可與配電網聯網運行，也可在電網故障時與配電網斷開孤島運行。

微網并入配電網后，配電系統的供電方式由傳統的輻射供電方式演變為雙端或多端供電模式，系統運行方式更為靈活，供電可靠性得到提高，但由于分布式電源的間隙性和隨機性也增加了配電系統可靠性分析的復雜性［2-6］。

含微網的配電系統可靠性評估問題，國內外學者已開展了很多研究。文獻［7］提出了虛擬電源的概念，用非序貫蒙特卡洛分析微網并入后對系統可靠性的影響。文獻［8］提出了一種含分布式風機、光伏陣列和蓄電池的配電系統準序貫蒙特卡洛可靠性評估方法。文獻［9］對含微網的配電系統供電可靠性進行分析，但認為分布式電源可提高微網內負荷的供電可靠性，對微網外負荷點的供電可靠性沒有影響。文獻［10］研究了配電網接入分布式電源后的孤島劃分模型，采用改進的最小路法分析含分布式電源的配電網供電可靠性。文獻［11］采用序貫蒙特卡洛法對加入風機后的配電網的可靠性進行分析。文獻［12］對風電場、光伏電池陣列和儲能系統的風光互補綜合發電系統的可靠性進行評估。文獻［13］分析了分布式電源在系統故障時的作用和轉帶負荷策略。然而鮮有文獻考慮風機、光伏系統的故障率和負荷的時變性。本文建立了分布式電源的出力模型，考慮負荷的時變特性，引入虛擬等值電源的概念，采用序貫蒙特卡洛模擬法研究含微網的配電系統可靠性評估，分析微網并入配電系統后對各區域負荷可靠性指標的影響。

1　系統元件模型

1.1風力發電系統出力

1.1.1風速模型

風速模型采用威布爾分布，兩參數威布爾分布將風速矢量當做隨機變量，則概率密度函數為

式中：c為尺度參數；k為形狀參數。

據反函數變化法理論得到威布爾分布風速發生器的風速為

1.1.2風力發電機的出力模型

風力發電機的出力可用分段函數近似表達［11］為

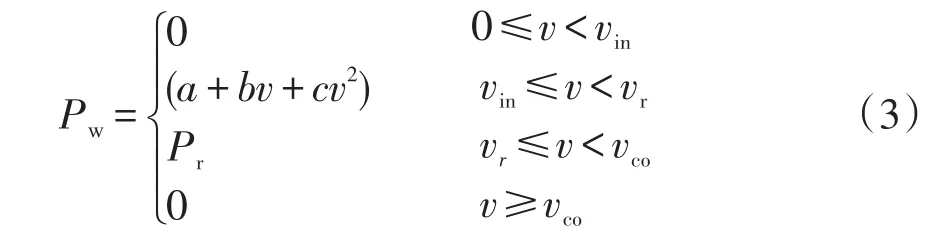
式中：Pw為風力發電機的輸出功率；Pr為風力發電機的額定功率；vin、vr和vco分別為風力發電機的切入、額定以及切出風速；a、b、c為相關參數［14］。

1.1.3風機故障率

風電場有e臺風機，風機正常運行的概率為D，故障的概率為U=1-D，則風電場有d臺風機正常工作的概率為

若風機的強迫停運率為 fi，抽取一個0～1的隨機數R，將R與 fi對比，決定風機i的狀態，即

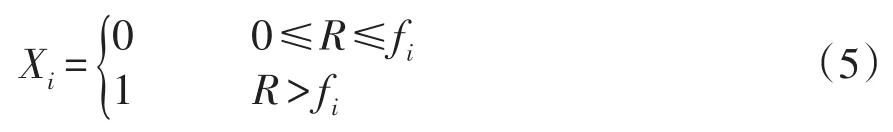
式中：0表示故障；1表示正常運行。

采用兩狀態抽樣法，則風機正常運行臺數為

1.2光伏發電系統出力

1.2.1光伏發電系統的出力模型

光伏發電系統主要由光伏電池陣列和電力電子器件等組成，光照強度時間序列模型可通過HOMER軟件得到，圖1是由HOMER軟件模擬得到的太原2014年全年內每小時的光照強度。

圖1　太原2014年全年的光照強度Fig.1　Solar irradiation intensity in Taiyuan，2014

光伏發電系統的出力［15］表示為

式中：PP為光伏陣列的輸出功率；Pn為光伏陣列的額定功率；Gb，i為第 i小時的光照強度；Gstd為標準環境給定的光照強度，通常取1 000 W/m2；Rc為特定光照強度，通常取150 W/m2。

1.2.2光伏發電系統故障率

光伏系統由光伏陣列和并網逆變器組成，光伏陣列中m塊光伏電池板串聯成一串，n串光伏電池板并聯接入逆變器，N個逆變器并聯接入電網。

并網逆變器的可靠性指標［16］為

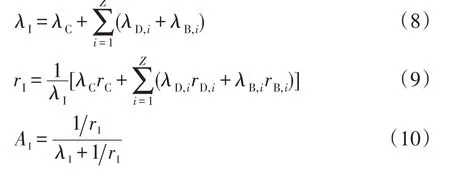
式中：λ為故障率；A為可利用率；r為停電時間；下標I、C、D和B分別指光伏逆變器、電容器、二極管和IGBT；i指第i個元件；Z為電容器、二極管和IGBT的總數。

m塊光伏電池板與熔斷器串聯后的故障率λS，i、故障停電時間rS，i、可利用率AS，i分別為

式中：λP，i和λF分別表示第i塊光伏電池板和熔斷器的故障率；rP，i和rF分別表示第i塊光伏電池板和熔斷器的停電時間。

n串光伏電池板并聯后的故障停電時間rSu1和故障率λSu1［17］分別為

n串光伏電池板中有nf個光伏電池板串正常工作的概率為

與逆變器串聯后，光伏-逆變器組的故障率λPV和故障停電時間rPV分別為

對光伏-逆變器組完全故障的概率為

1.3負荷模型

負荷模型與隨負荷的類型、位置和時間有關［18］。時間t的負荷可表示為

式中：Ly為年尖峰負荷；Pwe、Pd、Ph（t）分別為周負荷占年尖峰負荷、日負荷占周尖峰負荷和時間t負荷占日負荷的百分比。

一周內負荷隨時間的變化曲線如圖2所示。

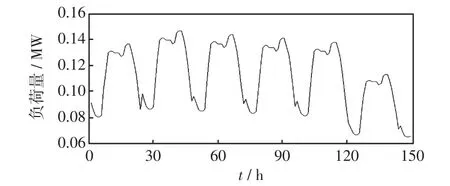
圖2　一周內負荷隨時間的變化曲線Fig.2　Time-varying load profile in one week

2　含微網的配電系統可靠性評估

2.1虛擬等值電源

含分布式電源的配電系統包含多個微電網，在可靠性分析時考慮微網中每個元件的狀態和新能源（風力、光伏）的間歇性特點，會使計算量加大。因此有必要把微網中的所有元件合成一個整體，用虛擬等值電源［7］VPP來表示，即

式中：PG為微網內部電源的輸出功率；LC為微網內部的負荷量。

微網與配電系統交換功率，若微網內部的發電容量滿足不了內部負荷的需求，則虛擬等值電源為負荷，VPP＜0；反之，虛擬等值電源為電源，VPP＞0，根據網絡拓撲結構和開關的類型，給微網外部區域負荷供電。

2.2切負荷策略

配電系統發生故障，網絡中的開關元件動作切除故障，隔離故障區域，一些負荷通過主供電網絡或分布式電源恢復供電，剩余負荷被切除，切除的負荷量取決于分布式電源所發容量和網絡結構。當微網內部發生故障，微網內部負荷全部停電；微網外部發生故障，若能有效隔離故障，并且虛擬等值電源VPP＞0，則根據網絡結構和開關位置，微網內部區域可不停電或停電時間僅為隔離時間；其他能由VPP供電的無微網區域負荷，若VPP大于該區域的負荷量，則該區域負荷可不停電或停電時間僅為隔離時間，否則一些負荷需要切除。

本文中設定含微網的配電系統可靠性評估中切除負荷的原則：首先切除子饋線負荷，然后切除連接在主饋線上的負荷，再切除下游區域負荷，最后上游區域負荷，直到VPP大于等于該區域的負荷量。

3　序貫蒙特卡洛法

采用序貫蒙特卡洛法對含微網的配電系統可靠性進行評估，其計算流程如下。

（1）產生一個0～1的隨機數R，根據元件的故障率λ，采用對數分布得到元件的無故障工作時間為

（2）計算系統中每個元件的無故障工作時間TTF。

（3）比較所有元件的TTF，找出最小的TTF（MTTF）和相對應的元件j。

（4）對元件 j，產生一個新的0～1隨機數R，根據元件j的修復率q和轉移率s，分別計算元件j的修復時間TTR和轉移時間TTS為

（5）判斷能恢復供電的負荷是由主網供電，還是由分布式電源供電。

（6）采用時變負荷模型，計算負荷點i在故障期間的平均負荷為

式中：Li（t）為時間t的負荷；te和ts分別為故障的始末時間。

（7）計算微網內部負荷的總容量為

式中，w為配電網系統中總的負荷點。

（8）采用兩狀態抽樣法計算在故障期間風機的正常運行臺數d。

（9）計算單臺風機的輸出功率Pw、風力發電系統輸出功率WG=dPw、光伏系統輸出功率Pp。

（10）微網內部電源的輸出功率為

式中，a、b為常數，微網內有風電場，則a=1，有光伏電站，則b=1，否則a=0、b=0。

（11）計算虛擬等值電源的輸出功率VPP=PG-LC。

（12）根據網絡結構、開關、熔斷器和VPP的運行模式，計算故障元件j引起負荷點i的停電時間為

式中，g為常數，g=1表示通過開關切換能恢復供電的元件，g=0表示其余不能恢復供電的元件，并對影響的負荷點記錄故障一次。

（13）元件j故障引起負荷點i的電能損失為

（14）將rij和ENSij分別與上一次的計算值疊加。

（15）重復步驟（12）～（14），計算所有影響的負荷點。

（16）對于故障元件j產生一個新的0～1隨機數R，轉換成TTF，將此TTF與步驟（1）計算的TTF相加，得到新的TTF；若新的TTF小于仿真年數TST，則進入步驟（3）；否則進入步驟（17）。

（17）在總仿真年數TST內，計算負荷點i的總的損失能量ENSi和總的停電時間ri分別為

式中，Ns為TST內影響負荷點i停電的故障次數之和。

（18）負荷點i的平均故障率λa，i、平均故障停電時間ra，i、年平均停電時間Ui和平均損失電能EENSi分別為

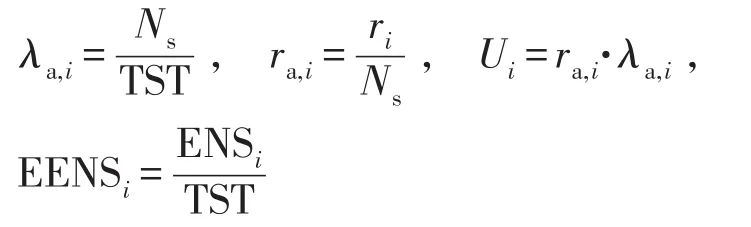
（19）系統電量不足期望值EENS、系統平均停電持續時間SAIDI、用戶平均停電持續時間CAIDI、平均供電可用率ASAI分別為

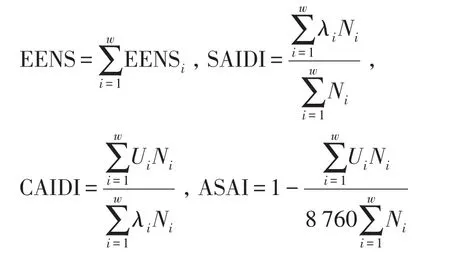
式中，Ni為節點i的負荷數量。

4　算例分析

本文采用序貫蒙特卡洛模擬的含微網的配電系統可靠性評估算法，對改造的IEEE RBTS Bus6系統進行分析。元件的可靠性參數見文獻［19-21］。元件的故障、修復和轉移時間采用對數分布。算例1為IEEE RBTS Bus6基本系統。算例2為有微網并入的IEEE RBTS Bus6改造后系統，見圖3。微網由風機和光伏發電系統組成，其中微網1區域內有50臺風機，每臺風機的功率為0.225 MW，機組的強迫停運率為0.04，切入、額定和切出風速分別為9 km/h、38 km/h、80 km/h，年平均風速為14.63 km/h，標準偏差為0.95。微網2區域內有光伏發電系統，由100塊電池板組成，每塊額定功率為0.235 MW，光伏發電系統的各部分故障參數見文獻［16］。

圖3　改造后的IEEE RBTS Bus6系統Fig.3　Modified IEEE RBTS Bus6 system

對2個算例進行對比，分析微網接入配電系統后對系統和負荷點可靠性水平的影響程度。算例1和算例2的系統可靠性指標見表1。

表1　系統可靠性指標參數對比Tab.1　Comparison of the system reliability indices

由表1可知，微網并入配電系統后，系統的可靠性指標SAIDI、CAIDI、EENS分別降低8.4%、8.6%、11%，系統的可靠性水平明顯提高。

算例1和算例2的負荷可靠性指標——年平均停電時間和電量不足期望值EENS分別見圖4和圖5。

從圖4和圖5可見，微網并入配電系統后，各負荷點的可靠性水平提高程度不同，其影響程度與網絡拓撲和負荷點的位置有關。微網并入配電系統前后對不同區域和負荷點的影響見表2。

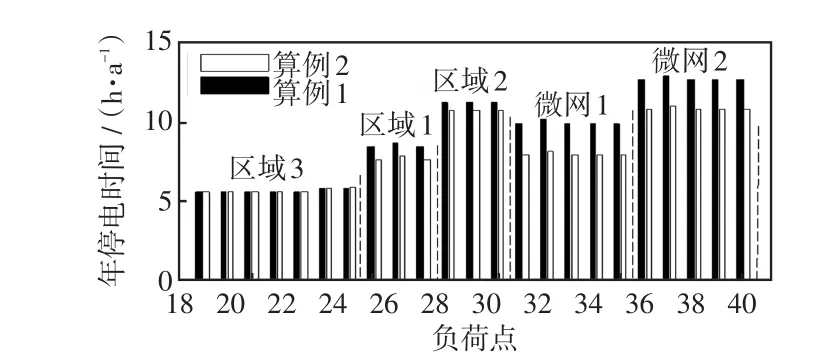
圖4　兩算例的負荷點年平均停電時間Fig.4　Average outage time at load points per year for two cases

圖5　兩算例負荷點的EENSFig.5　EENS at load points for two cases

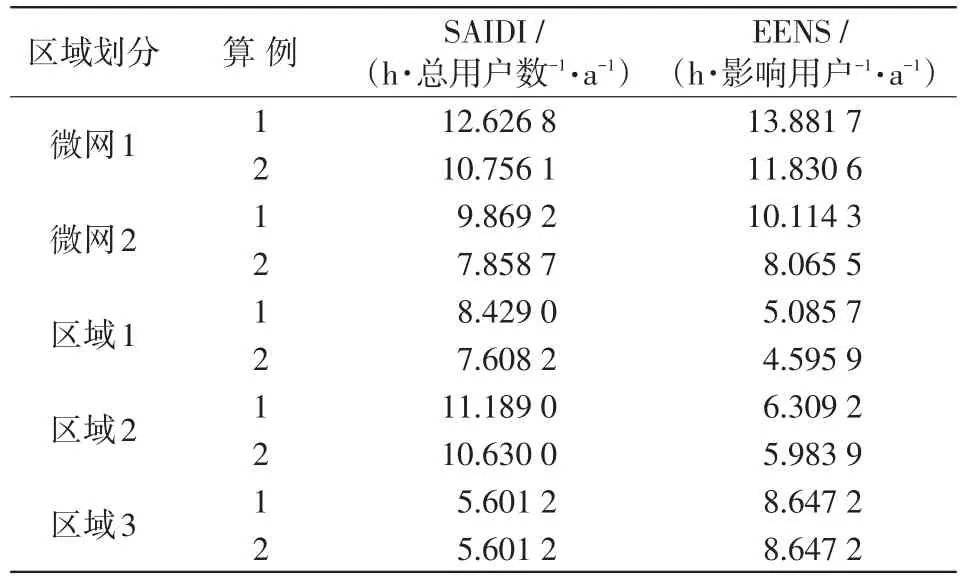
表2　各區域可靠性指標Tab.2　Reliability indices of two zones

微網并入配電網后，對有微網區域負荷點的可靠性指標影響很大，微網1和微網2內的可靠性指標（SAIDI、EENS）分別降低14.8%和20%；對無微網區域負荷點可靠性指標的影響程度與網絡的拓撲結構和負荷點與微網的相對位置有關，其中位于兩微網間的區域1的可靠性指標（SAIDI、EENS）降低10%，位于微網下游的區域2的可靠性指標（SAIDI、EENS）降低5%，位于兩微網上游的區域3的可靠性指標沒有變化。

5　結論

（1）本文研究了風力和光伏發電系統的特點，考慮風機和光伏發電系統的故障率，建立了分布式電源的出力模型和負荷的時變模型。

（2）引入虛擬等值電源的概念，提出了基于序貫蒙特卡洛模擬的含微網的配電系統可靠性評估算法，對改進的IEEE RBTS Bus6系統進行了可靠性評估驗證。

（3）微網并入配電網系統能有效提高系統的供電可靠性。分布式電源對微網區域內負荷的可靠性指標有很大影響，可提高微網內負荷的供電可靠性；無微網區域負荷點的可靠性指標與網絡拓撲和負荷點與微網的相對位置有關。

［1］魯宗相，王彩霞，閔勇，等（Lu Zongxiang，Wang Caixia，Min Yong，et al）.微電網研究綜述（Overview on microgrid research）［J］.電力系統自動化（Automation of Electric Power Systems），2007，31（19）：100-107.

［2］Roy Billinton，Ronald N Allan.Reliability Evaluation of Power Systems［M］.New York：Plenum Press，1996.

［3］殷桂梁，李相男，郭磊，等（Yin Guiliang，Li Xiangnan，Guo Lei，et al）.混合儲能系統在風光互補微電網中的應用（Application of hybrid energy storagy system on wind/solar hybrid microgrid）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（1）：49-53，59.

［4］王楓，祁彥鵬，傅正財（Wang Feng，Qi Yanpeng，Fu Zhengcai）.面向開關的復雜配電網可靠性評估簡化模型（Switch oriented simplified model of reliability evaluation of complex distribution system）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（2）：57-63.

［5］Billinton Roy，Gao Yi，Karki Rajesh.Composite system adequacy assessment incorporating large-scale wind energy conversion systems considering wind speed correlation［J］.IEEE Trans on Power Systems，2009，24（3）：1375-1382.

［6］Billinton R，Karki R，Yi Gao，et al.Adequacy assessment considerations in wind integrated power systems［J］.IEEE Trans on Power Systems，2012，27（4）：2297-2305.

［7］Bie Zhaohong，Zhang Peng，Li Gengfeng，et al.Reliability evaluation of active distribution systems including microgrids［J］.IEEE Trans on Power Systems，2012，27（4）：2342-2350.

［8］葛少云，王浩鳴，王源山，等（Ge Shaoyun，Wang Haoming，Wang Yuanshan，et al）.含分布式風光蓄的配電系統可靠性評估（Reliability evaluation of distribution system including distributed wind turbines，photovoltaic arrays and batteries）［J］.電力系統自動化（Automation of Electric Power Systems），2012，36（5）：16-23.

［9］梁惠施，程林，劉思革（Liang Huishi，Cheng Lin，Liu Sige）.基于蒙特卡羅模擬的含微網配電網可靠性評估（Monte Carlo simulation based reliability evaluation of distribution system containing micrograds）［J］.電網技術（Power System Technology），2011，35（10）：76-81.

［10］劉傳銓，張焰（Liu Chuanquan，Zhang Yan）.計及分布式電源的配電網供電可靠性（Distribution network reliability considering distribution generation）［J］.電力系統自動化（Automation of Electric Power Systems），2007，31（22）：46-49.

［11］Wang P，Billinton R.Time-sequential simulation technique for rural distribution system reliability cost/worth evaluation including wind generation as alternate supply［J］.IEE Proceedings—Generation，Transmission and Distribution，2001，148（4）：355-360.

［12］郭創新，張理，張金江，等（Guo Chuangxin，Zhang Li，Zhang Jinjiang，et al）.風光互補綜合發電系統可靠性分析（Reliability analysis of wind and photovoltaic integrated generating system）［J］.電力系統保護與控制（Power System Protection and Control），2013，41（1）：102-108.

［13］袁兆祥，孔祥玉，趙帥（Yuan Zhaoxiang，Kong Xiangyu，Zhao Shuai）.分布式電源接入配電系統可靠性分析方法（Reliability analysis method for distribution system with distributed generation）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2013，25（4）：112-116.

［14］Giorsetto P，Utsurogi K F.Development of a new procedure for reliability modeling of wind turbine generators［J］.IEEE Trans on Power Apparatus and Systems，1983，102（1）：134-143.

［15］Jeongje Park，Wu Liang，Jaeseok Choi，et al.A probabilistic reliability evaluation of a power system including solar/photovoltaic cell generator［C］//IEEE Power&Energy Society General Meeting.Calgary，Canada，2009.

［16］Zhang Peng，Wang Yang，Xiao Weidong，et al.Reliability evaluation of grid-connected photovoltaic power systems［J］.IEEE Trans on Sustainable Energy，2012，3（3）：379-389.

［17］王震，魯宗相，段曉波，等（Wang Zhen，Lu Zongxiang，Duan Xiaobo，et al）.分布式光伏發電系統的可靠性模型及指標體系（Reliability model and indices of distributed photovoltaic power system）［J］.電力系統自動化（Automation of Electric Power Systems），2011，35（15）：18-24.

［18］Wang Peng，Billinton Roy.Time sequential distribution system reliability worth analysis considering time varying load and cost models［J］.IEEE Trans on Power Delivery，1999，14（3）：1046-1051.

［19］Billinton R，Jonnavithula S.A test system for teaching overall power system reliability assessment［J］.IEEE Trans on Power Systems，1996，11（4）：1670-1676.

［20］Billinton R，Kumar S，Chowdhury N.A reliability test system for educational purposes-basic data［J］.IEEE Trans on Power Systems，1989，4（3）：1238-1244.

［21］Billinton R，Peng Wang.A generalized method for distributionsystemreliabilityevaluation［C］//IEEEWESCANEX’95 Communications Power and Computing Conference.Winnipeg，Canada，1995：349-354.

Reliability Evaluation on Distribution Systems Including Microgrids

ZHANG Haiyan1，2，HAN Xiaoqing1，XIAO Chun3，QIN Yabin4
（1.College of Electrical and Power Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.School of Computer Science and Control Engineering，North University of China，Taiyuan 030051，China；3.Customer Service Center of SEPC of SGCC，Taiyuan 030008，China；4.Maintenance Corporation of SEPC of SGCC，Taiyuan 030032，China）

Distributed generations（DGs）connected to a distribution grid have brought challenges to the reliability evaluation on distribution systems.A time-sequential Monte Carlo simulation technique is presented for the reliability evaluation on a distribution system including microgrid.Considering the intermittent and stochastic characteristics of DGs and forced outage rate of wind turbine generation and photovoltaic system，the power output model of microgrid and time-varying load model are built.The concept of virtual power plant（VPP）is introduced to evaluate the reliability at the load points in distribution system including microgrid.The effectiveness of the proposed method is verified by the test on an modified IEEE RBTS Bus6 system.

time-sequential Monte Carlo method；reliability evaluation；virtual power plant（VPP）；microgrid

TM461

A

1003-8930（2016）10-0012-06

10.3969/j.issn.1003-8930.2016.10.003

2015-03-06；

2015-12-26

國家自然科學基金資助項目（51277127）；山西省高等學校中青年拔尖創新人才支持計劃資助項目

張海燕（1980—），女，博士研究生，講師，研究方向為電力系統可靠性分析、電力系統運行與控制、能量管理系統等。Email：zhanghaiyanhaorui@163.com

韓肖清（1964—），女，博士，教授，博士生導師，研究方向為電力系統運行與控制、新能源與微電網運行等。Email：hanxiaoqing@tyut.edu.cn

肖春（1987—），女，碩士，助理工程師，研究方向為配電系統的可靠性評估、電力系統運行與控制。Email：tyutxiaochun@163.com