基于改進ITD邊際譜熵的單相自適應重合閘

周　超，黃　純，江亞群，杜培偉，朱永強，康志豪

（湖南大學電氣與信息工程學院，長沙 410082）

基于改進ITD邊際譜熵的單相自適應重合閘

周超，黃純，江亞群，杜培偉，朱永強，康志豪

（湖南大學電氣與信息工程學院，長沙 410082）

基于固有時間尺度分解ITD算法，提出了改進ITD算法：針對波形失真問題，引入了有理樣條函數插值和極值點延拓；針對虛假分量問題，增加了能量判據作為迭代終止條件。把改進ITD算法與邊際譜熵相結合，用于判別高壓輸電線路單相接地故障類型。首先ITD分解兩種故障相電弧電壓獲得邊際譜，然后分析對比了兩種故障邊際譜的特點，從時頻域定性揭示了兩種故障相電弧電壓及其邊際譜的差異，再根據信息熵原理，得出ITD邊際譜熵來快速準確識別兩種故障類型。結果表明：輸電線路瞬時性故障時，熵值大于等于0.2；永久性故障時，熵值小于0.2。針對輸電線路單相接地故障的仿真結果，驗證了該方法有效、可行。

單相自適應重合閘；固有時間尺度分解；邊際譜熵；瞬時性故障；永久性故障

超高壓輸電線路是電力系統的重要部分，它肩負著傳送功率和聯絡各個系統的重任，但不可避免地也會發生短路故障，實際運行經驗表明單相接地短路故障的發生率超過了90%，其中80%以上都為瞬時性故障。為提高電力系統的運行穩定性和供電連續性，高壓輸電線路常采用單相重合閘技術［1］。

近年來，自適應重合閘成為了電力工程界的熱點和難點問題。國內外專家提出的區別永久性和瞬時性故障的判據主要有3類。①基于恢復電壓特性的判據，文獻［2］分析了瞬時性故障情況下恢復電壓的拍頻特性，利用斷開相恢復電壓的瞬時最大值與最小值的比作為故障類型判據；文獻［3］通過對斷開相恢復電壓在一個工頻周期內進行積分，提出了故障性質積分判據。但對于帶并聯電抗器的輸電線路，恢復電壓比較低，不便于檢測。②基于瞬時性故障電弧特性判據，由于輸電電壓等級提高與快速斷路器的使用，一次電弧時間大大減少，根據一次電弧［4］判別故障類型比較困難。③基于故障信號非線性的特點，在重合閘技術中應用非線性信號分解方法處理故障信號得出故障判據，主要方法有小波變換［5］、S變換［6］、經驗模態分解EMD（empirical mode decomposition）［7-8］、原子分解法［9-10］等。這些方法在重合閘領域取得了較好的效果，但其自身也存在著缺陷。例如小波變換缺乏自適應性，而且受小波基函數選擇的限制和噪聲的影響，分解效果不理想；S變換分解的信息過多，自適應能力較差；EMD有較好的自適應，雖然克服了小波變換、S變換在傳統時頻分析方法中的缺陷，但EMD易出現欠包絡、過包絡現象，具有端點效應、迭代終止等問題［8］；原子分解法對于如何構造故障電壓相關原子庫還有待研究［10］。

文獻［11］提出了一種分析非平穩信號的新算法—固有時間尺度分解ITD（intrinsic time-scale decomposition），它是在研究EMD和局部均值分解LMD（local mean decomposition）的基礎上提出的一種自適應時頻分析方法，可以將任意復雜信號分解成若干個有實際物理意義的固有旋轉分量PRC（proper rotation component）和一個殘余分量，具有時頻分辨率高、運算速度快、能過濾噪聲等優點，但也存在著波形失真、虛假分量等缺點。

信息熵作為一種定性衡量信號或者系統狀態不確定性程度的指標，能夠有效提取信息源特征。結合小波變換、小波能量相對熵、小波奇異熵等在電力系統故障選線、故障選相、繼電保護等方面有了廣泛的應用。文獻［12］提出了小波能量相對熵的配電網故障選線判據；文獻［13］提出了小波熵理論在電力系統故障檢測中的應用；結合原子分解法與信息熵，文獻［14］將原子分解能量熵用于低頻振蕩主導模式檢測。

高壓輸電線路故障信號是一種非平穩、多頻段的復雜信號，本文采用改進ITD算法分解高壓輸電線路故障信號可得到反映故障相暫態電壓由高頻到低頻的振動模態，對振動模態進行邊際譜熵復雜度分析，能準確反映故障類型，與直接求取熵值相比，減少了特征信號之間的耦合與干擾。不同的故障信號復雜度不同，邊際譜熵也不同，可以作為故障信號的判據。

1　改進ITD及其邊際譜熵

1.1ITD及其改進算法基本原理

EMD、LMD和ITD進行比較，3種算法的主要區別在于基函數的構造方式不同。EMD通過求取信號上下極值點包絡線構造基函數，LMD通過求取局部均值包絡線來構造基函數，而ITD是基于信號本身的線性變換來構造基函數。和EMD、LMD一樣，ITD也會出現PRC分量失真問題［15］，因此，采用有理樣條函數插值來代替線性變換，并對極值點進行鏡像延拓來處理波形失真問題；針對分解過程出現的虛假分量問題，引入了能量判據。改進ITD算法流程如圖1所示，其分解步驟如下。

（1）確定原信號x（t）（t≥0）的極值x（k）及對應的時刻τ（k）（k=1，2，…，M，M為極值點個數），并計算

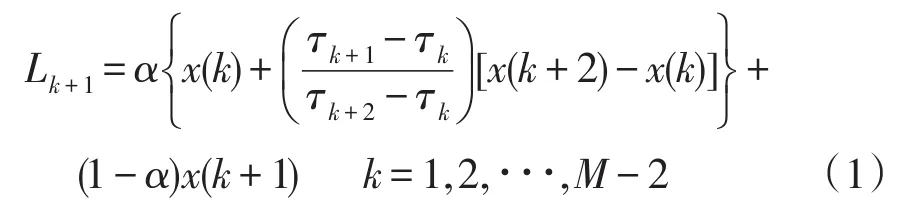
式中，0＜α＜1，一般取α=0.5。

（2）由式（1）可知Lk值是從L2到LM-1，兩端點L1、LM的值需要估計計算。參照EMD中端點延拓方法，采用鏡像延方法將極值點向左右兩端各延拓一個，得到左右兩端極值點分別為 （τ0，x0）、（τM+1，xM+1），令k分別等于0和M-1，按照式（1）求出L1、LM的值。

（3）用有理樣條函數擬合出所有的L1，L2，…，LM，得到基線信號BL1（t），從原信號中分離出基線信號，即h1（t）=x（t）-BL1（t）。若h1（t）滿足PRC條件［15-16］，輸出h1（t），令PRC1=h1（t）；否則h1（t）作為原始數據，繼續重復上述步驟，直到h1k（t）滿足PRC條件，記PRC1=h1k（t）。

（4）將 PRC1從原始信號中分離出來，則u1（t）=x（t）-PRC1，得到新的剩余信號u1（t）。

（5）將u1（t）作為原始數據，重復上述步驟（1）～（4），循環n-1次，直到剩余信號un（t）為單調信號或常信號。但是在實際工程應用中，在對分析結果沒有影響的情況下，只提取信號的主導能量模式可提高分解速度，因此ITD分解終止條件可適當放寬，將信號能量添加到分解中作為終止條件判據，即

式中：l為信號序列的長度；上標z表示信號序列的均值；本文中ε取0.1，即剩余信號能量小于原信號能量的10%時，ITD分解結束，則原始信號被分解為

ITD算法提出了一種以全波為單位來計算瞬時幅值、瞬時頻率和瞬時相位的方法。半波是指2個過零點間的信號，全波是指2個相鄰的上過零點間的信號，單調區間是指相鄰2個極值點間的信號［11］，則瞬時相位θt定義為

式中：A1和A2分別表示全波中正半波和負半波的幅度，A1＞0，A2＞0；t1和t5為2個上過零點時刻；t3為下過零點時刻；t2為正半波極大值點A1時刻；t4為負半波極小值點-A2時刻。

圖1　本文算法的流程Fig.1　Flow chart of the proposed method

于是，對瞬時相位θt微分得瞬時頻率為

瞬時幅值At以半波為單位定義，即2個過零點間信號極值點的值，在每個半波內At為定值，即

為了考察改進ITD分解效果，選取文獻［17］中的調幅-調頻信號x（t）作為對比，即

ITD算法和改進ITD算法仿真波形如圖2和圖3所示，改進ITD算法可以很好地分解得到原始信號中的每個調幅、調頻分量，各個PRC分量和殘余分量可以較為準確地重構測試信號，x0（t）為重構信號。改進ITD算法端部效應好于ITD算法，虛假分量少，迭代分解時間較少。

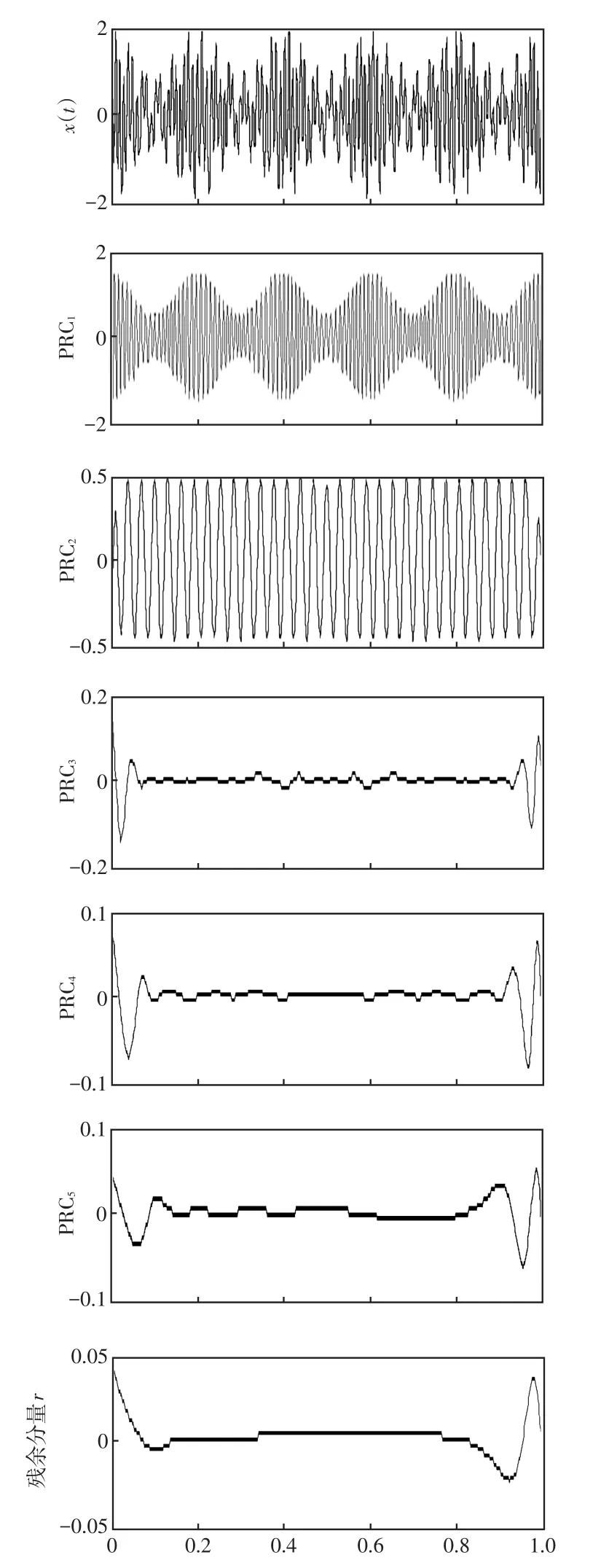
圖2　ITD分解結果Fig.2　Results of ITD decomposition

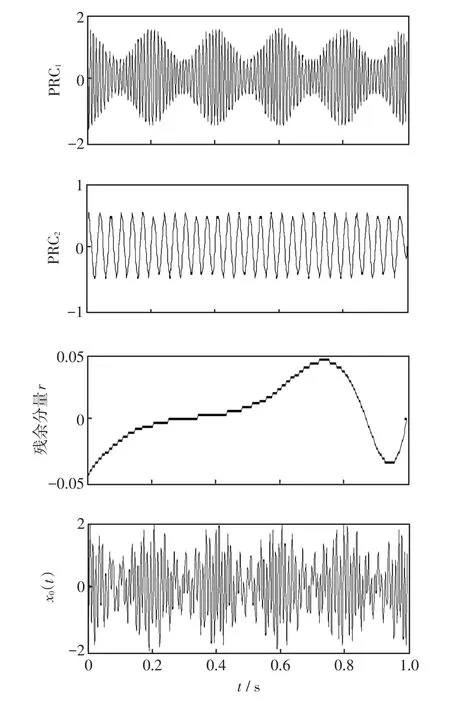
圖3　改進ITD分解結果Fig.3　Results of improved ITD decomposition

1.2基于改進ITD算法的邊際譜熵

信息熵的定義：若B為可測集合H生成的σ代數和具有μ測度，μ（B）=1的勒貝格空間，且空間B可以表示為有限劃分B=｛Bi｝中互不相容的集合形式，即，且Bi?Bj=?，?i≠j，則該劃分B的信息熵［17］可表示為

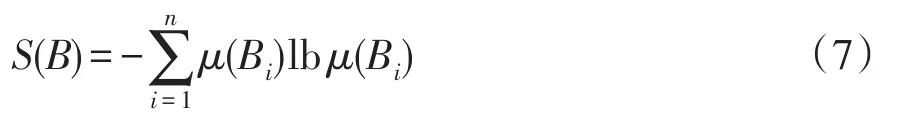
由定義可知，信息熵是指信息源中某件事發生時，包含的信息量大小，信號源越復雜、信號模式越多，則熵值越大。

由式（5）和式（6）可以看出瞬時頻率和幅值的表達式都為時間的函數，故將信號幅度在三維空間中表示成時間和頻率的函數H（f，t），于是定義ITD的時頻分布為

式中：Re表示取其實部；Bi（t）為瞬時幅值；fi（t）為瞬時頻率。

對H（f，t）進行時間積分，可得到ITD算法邊際譜，即

對離散的頻率點 f（kΔf），信號邊際譜可表示為

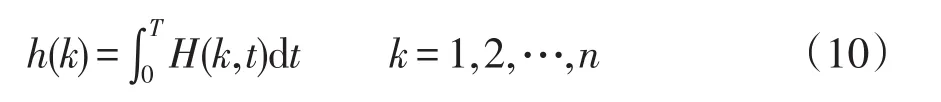
式中：n為在所分析信號頻率帶內頻率離散點的個數；T為信號時間長度。

根據信息熵理論，定義ITD算法邊際譜熵為

式中，pk為第k個頻率所對應的幅值出現的概率，將熵值歸一化為 0～1，即有，L為h（k）序列的長度。

2　基于改進ITD算法邊際譜熵的單相自適應重合閘原理

2.1單相接地故障時域特征分析

由文獻［5］提出的輸電線路瞬時性故障二次電弧數學方程式，利用ATP-EMTP仿真軟件中的MODEL模塊構造二次電弧模型。EMTP仿真模擬500 kV輸電線路在0.05 s故障，0.10 s斷路器跳閘，0.30 s熄弧，得到瞬時性故障中二次電弧燃燒時電壓波形，見圖4。在斷路器跳閘后用線性電阻代替電弧模型，得到永久性故障電弧電壓波形，見圖5。

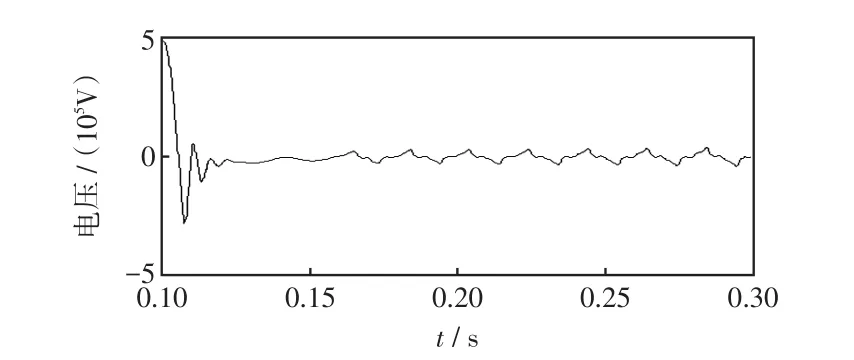
圖4　瞬時性故障點二次電弧電壓波形Fig.4　Secondary arc voltage waveform of transient fault

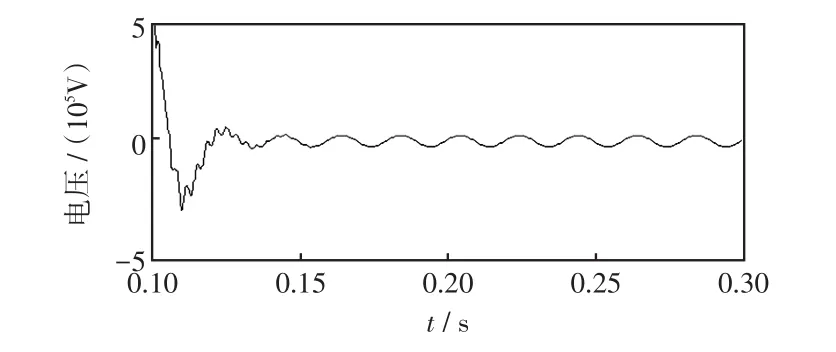
圖5　永久性故障點電弧電壓波形Fig.5　Arc voltage waveform of permanent fault

分析可知，當系統發生單相接地短路故障后，故障相兩端線路斷開，由于電感、電容儲能元件的存在，不管是永久性還是瞬時性故障，在跳閘初期，線路端電壓都將存在大量暫態諧波，故障相電壓的時域分布比較接近。若線路發生永久性故障，一次電弧熄滅后故障持續存在，線路端電壓中的暫態諧波衰減速度很快，絕大部分會在2～3個周期內能量衰減到接近0；若線路發生瞬時性故障，由于故障相二次電弧非線性的影響，線路電壓中的諧波分量衰減較慢，諧波畸變程度比較高，使故障相電壓發生畸變。二次電弧階段，電弧要經過燃燒、熄滅、重燃、熄滅的反復過程，且電弧持續燃燒的時間比較長，當電弧重燃電壓小于電弧電壓后，電弧才能真正的熄滅。所以兩類故障在跳閘后斷開故障相電壓在時域分布上是不一樣的，且瞬時性故障暫態電壓信號比永久性故障時要復雜得多。圖6（a）為永久性故障相電壓波形，圖6（b）為瞬時性故障相電壓波形。

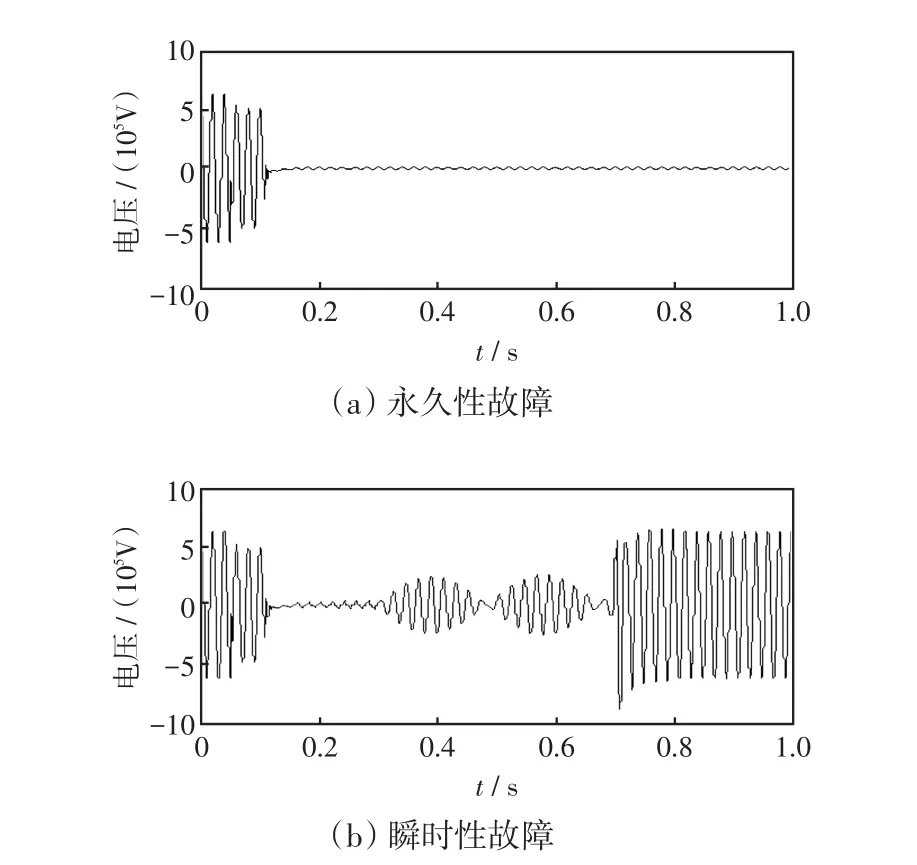
圖6　不同故障類型的相電壓波形Fig.6　Phase voltage waveforms of different fault types

2.2單相接地故障頻域特征分析

運用改進ITD算法分解如圖4和圖5所示的兩種故障類型電弧電壓信號序列，得到各個頻段的PRC。由式（5）和式（6）求取各個分量的瞬時頻率ft和瞬時幅值At，將 ft、At代入式（8）和式（9）中得到邊際譜。對永久性故障跳閘后故障相端電壓進行頻譜分析，得到永久性故障電弧邊際譜，如圖7所示。對瞬時性故障二次電弧時的端電壓進行頻譜分析，得到瞬時性故障二次電弧邊際譜，如圖8所示。可以看出，永久性故障時，頻率比較單一，瞬時性故障由于二次電弧高度非線性的特點，線路中將存在大量高次諧波，主要有幅值較大的3、5、7、9、11次諧波等，且能量主要集中在600 Hz以內。從圖7和圖8可以看出，瞬時性故障的邊際譜要比永久性故障的復雜很多。

圖7　永久性故障電壓邊際譜Fig.7　Voltage marginal spectrum of permanent fault

圖8　瞬時性故障電壓邊際譜Fig.8　Voltage marginal spectrum of transient fault

2.3故障類型判別算法步驟

用改進ITD算法進行輸電線路故障類型判別，步驟如下：

（1）對輸電線路發生故障后的電壓信號進行仿真模擬實驗，測試數據見圖6，提取斷路器跳閘后的8個工頻周期電壓信號序列作為測試數據；

（2）對采樣時間窗內的數據進行改進ITD分解，則故障電壓信號可以分解為若干個不同頻率的固有旋轉分量：PRC1，PRC2，···，PRCn；

（3）將分解得到能量較大的前n個固有旋轉分量作為特征分量，由式（4）～式（6）提取特征分量的瞬時幅值和瞬時頻率，根據式（9）～式（11）求取邊際譜熵，并進行歸一化處理；

（4）選取閾值Pset，比較邊際譜熵的大小，確定輸電線路故障類型，若熵值大于Pset，則輸電線路為瞬時性故障，否則為永久性故障。

3　單相自適應重合閘仿真驗證分析

本文利用ATP-EMTP對如圖9所示的500 kV輸電線路進行仿真分析，為了和文獻［7］采用的EMD近似熵算法對比，線路采用分布參數模型，參數如下：

式中：R1、L1、C1為輸電線路正序電阻、電感、電容；R0、L0、C0為線路零序電阻、電感、電容；ZM1、ZM0、ZN1、ZN0分別為系統M、N側正序、零序阻抗；Zp、Zn為并聯電抗器。

為了驗證不同外界因素對該重合閘算法結果造成的影響，本文對M、N兩側系統的不同相對阻抗角、不同故障位置（故障點到輸電線路M端的距離與線路總長度的比）、金屬性接地以及經過渡電阻接地的永久性和瞬時性故障進行了大量仿真驗證，部分結果如表1所示。

圖9　500 kV輸電線路仿真模型Fig.9　Simulation model for 500 kV transmission line

表1　部分故障條件下的測試結果Tab.1　Test results of part of the fault conditions

從表1可以看出，永久性故障時，燃弧時間比較短，故障電壓信號中僅有單一頻率的工頻信號，其邊際譜熵歸一化值很小；瞬時性故障時，二次電弧期間故障相端電壓含有大量高次諧波，頻率成分相當復雜，其邊際譜熵歸一化值遠大于0。兩種故障類型下，利用電弧電壓邊際譜熵的顯著差異，可以設定合理的閾值，準確識別故障性質，與文獻［7］得出的結論一致。由表1可知，永久性故障的熵值在0附近，瞬時性故障的熵值在0.4附近，可選取有較大裕度的閾值Pset=0.2。結果表明：輸電線路發生瞬時性故障時的故障相端電壓信號相對于永久性故障來說，頻率成分要復雜，可以通過邊際譜熵值體現出來；此算法能夠在8個周波內準確識別輸電線路故障類型，并且該方法不受系統相對阻抗角、過渡電阻、短路點位置的影響，適用于高壓輸電線路單相自適應重合閘，可快速準確判斷故障類型，提高重合閘成功率。

4　結論

（1）改進ITD方法采用殘余能量小于某一閾值作為迭代終止條件，減少了虛假分量的出現，提高了分解速度；采用端點延拓，解決了分量失真問題。

（2）利用改進ITD邊際譜熵區分輸電線路故障類型，邊際譜熵大于等于0.2，則為瞬時性故障；邊際譜熵小于0.2，則為永久性故障。

［1］陳誠，江亞群，黃純（Chen Cheng，Jiang Yaqun，Huang Chun）.輸電線路單相瞬時性故障熄弧判定方法（An approach to judge extinction arc of single-phase transient fault in transmission lines）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（11）：21-25.

［2］石光，邵文權，郭耀珠，等（Shi Guang，Shao Wenquan，Guo Yaozhu，et al）.帶并聯電抗器的超/特高壓輸電線路的單相重合閘新方案（Single-phase adaptive reclose scheme for EHV/UHV transmission lines with reactors）［J］.電力自動化設備（Electric Power Automation Equipment），2011，31（7）：5-9.

［3］曹芬，何奔騰（Cao Fen，He Benteng）.帶并聯電抗器的超高壓輸電線路單相自適應重合閘新算法（New algorithm for single-phase adaptive reclosure of EHV transmission lines with shunt reactor）［J］.電力系統自動化（Automation of Electric Power Systems），2009，33（23）：55-59，107.

［4］劉海峰，林湘寧，劉沛（Liu Haifeng，Lin Xiangning，Liu Pei）.基于形態學閉開-開閉梯度變換的單相自適應重合閘方案（An adaptive single-phase auto-reclosure scheme based on morphological close-opening-open-closing gradient transform）［J］.電力系統自動化（Automation of Electric Power Systems），2005，29（21）：39-44.

［5］程玲，徐玉琴，宋秭霖（Cheng Ling，Xu Yuqin，Song Zilin）.基于電弧小波譜能量分析的輸電線路單相自適應重合閘（Single-pole adaptive reclosure of transmission line based on arc models and wavelet spectrum energyanalysis）［J］.電網技術（Power System Technology），2007，31（24）：81-85.

［6］趙妍，高磊，王永，等（Zhao Yan，Gao Lei，Wang Yong，et al）.基于S變換奇異值能量熵的單相自適應重合閘故障符號識別法（A method to recognize fault symbol for adaptive single-phase reclosure based on energy entropy of singular value from S-transform）［J］.電網技術（Power System Technology），2012，34（12）：209-213.

［7］蘭華，艾濤，張桂蘭（Lan Hua，Ai Tao，Zhang Guilan）.基于經驗模態分解及近似熵的輸電線路單相自適應重合閘（Single-phase adaptive reclosure of transmission lines based on EMD and approximate entropy）［J］.電網技術（Power System Technology），2009，33（20）：211-214.

［8］劉志剛，李文帆，孫婉璐（Liu Zhigang，Li Wenfan，Sun Wanlu）.Hilbert-Huang變換及其在電力系統中的應用（Hilbert-Huang transform and its applications in power system）［J］.電力自動化設備（Electric Power Automation Equipment），2012，32（4）：109-116.

［9］賈晶晶，龔慶武，李勛，等（Jia Jingjing，Gong Qingwu，Li Xun，et al）.采用原子分解法的帶并聯補償線路單相自適應重合閘（Single-phase adaptive reclose of shunt compensated transmission lines using atomic decomposition）［J］.電力系統自動化（Automation of Electric Power Systems），2013，37（5）：117-123.

［10］王寧，李林川，賈清泉，等（Wang Ning，Li Linchuan，Jia Qingquan，et al）.應用原子分解的電能質量擾動信號分類方法（Classification of power quality disturbance signals using atomic decomposition method）［J］.中國電機工程學報（Proceedings of the CSEE），2011，31（4）：51-58.

［11］Frei M G，Osorio I.Intrinsic time-scale decomposition：time-frequency-energy analysis and real-time filtering of non-stationary signals［J］.Proceedings of the Royal Society of London A，2007，463（2078）：321-342.

［12］束洪春，彭仕欣（Shu Hongchun，Peng Shixin）.利用全頻帶綜合小波能量相對熵的配網故障選線方法（Distribution network fault line detection using the full waveband complex relative entropy of wavelet energy）［J］.高電壓技術（High Voltage Engineering），2009，35（7）：1559-1564.

［13］何正友，蔡玉梅，錢清泉（He Zhengyou，Cai Yumei，Qian Qingquan）.小波熵理論及其在電力系統故障檢測中的應用研究（A study of wavelet entropy theory and its application in electric power system fault detection）［J］.中國電機工程學報（Proceedings of the CSEE），2005，25（5）：38-43.

［14］李勛，龔慶武，賈晶晶（Li Xun，Gong Qingwu，Jia Jingjing）.采用原子分解能量熵的低頻振蕩主導模式檢測方法（A detection method for low frequency oscillation dominant modes based on atomic decomposition energy entropy）［J］.中國電機工程學報（Proceedings of the CSEE），2012，32（1）：131-139.

［15］程軍圣，李海龍，楊宇（Cheng Junsheng，Li Hailong，Yang Yu）.改進ITD和能量矩在齒輪故障診斷中的應用（Based on the improved ITD and energy moment to diagnose the gear）［J］.振動、測試與診斷（Journal of Vibration，Measurement&Diagnosis），2013，33（6）：954-959，1091.

［16］安學利，蔣東翔，劉超，等（An Xueli，Jiang Dongxiang，Liu Chao，et al）.基于固有時間尺度分解的風電機組軸承故障特征提取（Bearing fault feature extraction of wind turbine based on intrinsic time-scale decomposition）［J］.電力系統自動化（Automation of Electric Power Systems），2012，36（5）：41-44，102.

［17］陳非，黃樹紅，張燕平，等（Chen Fei，Huang Shuhong，Zhang Yanping，et al）.基于信息熵距的旋轉機械振動故障診斷方法（Research on diagnosis of vibration faults rotating machinery based on distance of information entropy）［J］.振動、測試與診斷（Journal of Vibration，Measurement&Diagnosis），2008，28（1）：9-13，74-75.

Single-phase Adaptive Reclosure Based on Marginal Spectrum Entropy Using Improved ITD

ZHOU Chao，HUANG Chun，JIANG Yaqun，DU Peiwei，ZHU Yongqiang，KANG Zhihao
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

An improved intrinsic time-scale decomposition（ITD）algorithm is presented：for waveform distortion，rational spline function interpolation and extrapolation at extreme points are introduced；for false weight，the energy criterion is added as the termination condition for iteration.The improved ITD algorithm and marginal spectrum entropy are combined to distinguish the single-phase ground fault types for high-voltage transmission line：first，ITD decomposes two faults with arc voltage to obtain the marginal spectrum，then the characteristics of marginal spectrum are compared，and the difference in the marginal spectrum of fault phase voltages from time-frequency domain is revealed；according to the information entropy principle，the ITD marginal spectrum entropy can distinguish between two fault types rapidly and accurately.The results show that when the transmission line is with transient fault，the entropy value is greater than 0.2；and with permanent fault，the entropy value is less than 0.2.The simulation results of transmission line with singlephase ground fault demonstrate that the proposed algorithm is effective and feasible.

single-phase adaptive reclosure；intrinsic time-scale decomposition（ITD）；singular spectrum entropy；transient fault；permanent fault

TM727.2

A

1003-8930（2016）10-0024-07

10.3969/j.issn.1003-8930.2016.10.005

2015-03-06；

2016-01-19

國家高技術研究發展計劃（863計劃）資助項目（2012AA050215）；國家電網公司科技資助項目（5216A313500N）

周超（1990—），男，碩士研究生，研究方向為電氣信號檢測、電力系統繼電保護。Email：935850757@qq.com

黃純（1966—），男，博士，教授，博士生導師，研究方向為電能質量分析與控制信號處理方面研究。Email：yellowpure@hotmail.com

江亞群（1971—），女，博士，副教授，碩士生導師，研究方向為智能電網和電能質量分析與控制方面研究。Email：yaqunjiang@foxmail.com