概率難點輕松突破

金楊建浦敘德

概率難點輕松突破

金楊建浦敘德

事件發生的可能性有大有小.概率是度量事件發生可能性大小的一個量，在實際生活中有著廣泛的應用，概率也是初中數學較為重要的一個知識點.初中教材中與概率相關的內容共出現了三次∶第一次是在八年級下冊《認識概率》，從中我們知道了概率的定義，并知道可以用頻率的穩定值估計概率；第二次就是本章《等可能條件下的概率》，從中我們又知道了等可能性的概念，并會通過合適的方法求等可能條件下的概率；最后一次出現在九年級下冊《概率的簡單應用》，顧名思義，就是運用概率進行估計、判斷、決策……幫助我們解決一些實際問題.可見，本章在整個初中階段概率內容的學習中起到承上啟下的作用.

一、緊扣概念，精準判定

教材中等可能性概念是“一般地，設一個試驗的所有可能發生的結果有n個，它們都是隨機事件，每次試驗有且只有其中的一個結果出現.如果每個結果出現的機會均等，那么我們說這n個事件的發生是等可能的，也稱這個試驗的結果具有等可能性.”

我們可以把這個概念濃縮成2句話：①試驗結果有多個，但每次有且只有一個結果出現；②結果出現是隨機的，但每個結果出現機會均等.

結合這2句話，我們就可以判斷某試驗的結果是否具有等可能性，并可以求出某種結果發生的概率.

例1（2016·江蘇淮安）一個不透明的袋子中裝有3個黃球和4個藍球，這些球除顏色外完全相同，從袋子中隨機摸出一個球，摸出的球是黃球的概率是________.

【分析】本題摸到的球有7種不同的結果：黃1，黃2，黃3，藍1，藍2，藍3，藍4，并不是只有黃球或藍球這兩種可能，即摸到黃球和籃球不是等可能的，故摸到黃球的概率不是.

【解答】因為一個不透明的袋子中裝有3個黃球和4個藍球，而摸出每個球是等可能的，即所有等可能的結果數為7，而摸到黃球的結果數為3，所以摸出的球是黃球的概率是.

二、有無“放回”，謹慎判斷

一般地，如果一個試驗有n個等可能的結果，當其中的m個結果之一出現時，事件A發生，那么事件A發生的概率P（A）=，其中m為事件A發生可能出現的結果數，n為所有等可能出現的結果數.對于試驗過程并不復雜的問題，如上例，只要能緊扣概念，便不會出現問題.而對于試驗步驟較復雜的問題，則需要謹慎地判斷試驗中前一個步驟與后一個步驟有無區別，即要考慮“摸球有無放回”.

例2（2016·江蘇鹽城）一個不透明的袋子中有大小、質地完全相同的4只小球，小球上分別標有1、2、3、4四個數字.

（1）從袋中隨機摸出一只小球，求小球上所標數字為奇數的概率；

（2）從袋中隨機摸出一只小球，再從剩下的小球中隨機摸出一只小球，求兩次摸出的小球上所標數字之和為5的概率.

【分析】第（2）問說明試驗有兩步，第1步是從4只小球中隨機摸1只，而第2步是從剩下的小球，也就是3只小球中隨機摸1只，是“無放回的摸球游戲”.所以在解答時要謹慎對待.

1 2 3 4 1 3 4 5 2 3 5 6 3 45 7 4 5 6 7

共有12種等可能的結果，其中兩次摸出的小球上所標數字之和為5的可能性有4種，所以P（兩次摸出的小球數字之和為

方法二（樹狀圖）

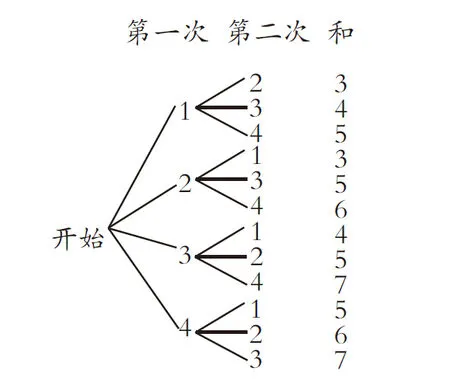
共有12種等可能的結果，其中兩次摸出的小球上所標數字之和為5的可能性有4種，所以P（兩次摸出的小球數字之和為5）=

三、圖表有別，合理選擇

從例2中，我們可以看出，對于步驟為兩次的試驗，可以通過列表法或樹狀圖的方法找出所有的等可能結果數以及事件發生可能出現的結果數.但對于不同情形的問題，是不是都適合用這兩種方法呢？

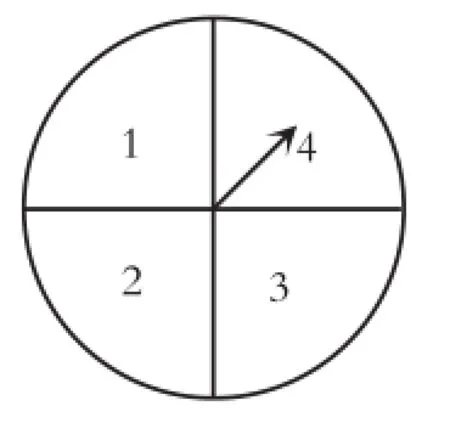
例3（2016·蘭州）小明和小軍兩人一起做游戲，游戲規則如下：每人從1，2，…，8中任意選擇一個數字，然后兩人各轉動一次如圖所示的轉盤（轉盤被分為面積相等的四個扇形），兩人轉出的數字之和等于誰事先選擇的數，誰就獲勝；若兩人轉出的數字之和不等于他們各自選擇的數，就再做一次上述游戲，直至決出勝負.若小軍事先選擇的數是5，用列表或畫樹狀圖的方法求他獲勝的概率.

【分析】本題是可以用樹狀圖或列表法進行研究的，但是因為試驗有兩個步驟，且每個步驟均有4種等可能的結果，如果用樹狀圖，則答題時會因為“樹枝”較多，導致答題區域過大，甚至會出現雜亂無章的可能，因此，建議對于試驗步驟是兩次，且每個步驟有3個（或以上）結果時用列表法（試題有明確要求的除外）.

解答：列表如下：

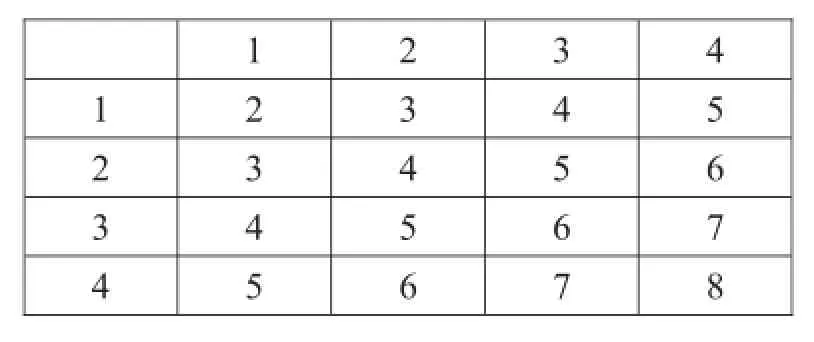
1 2 3 4 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8

所有等可能的情況有16種，其中兩次指針所指數字的和為5的情況有4種，所以小軍獲勝的概率=

例4（2009·江蘇）一家醫院某天出生了3個嬰兒，假設生男生女的機會相同，那么這3個嬰兒中，出現1個男嬰、2個女嬰的概率是多少？

【分析】列表法的優點在于處理試驗步驟僅有2個，且當每個步驟可能的結果數較多時，能夠清楚、簡潔地刻畫所有等可能的結果數以及事件發生可能出現的結果數，但對于步驟超過2的試驗，則無能為力.3個嬰兒的性別，相當于試驗步驟有三次，因此，只能用樹狀圖來研究.

【解答】用樹狀圖分析如下：

第一個第二個第三個所有結果

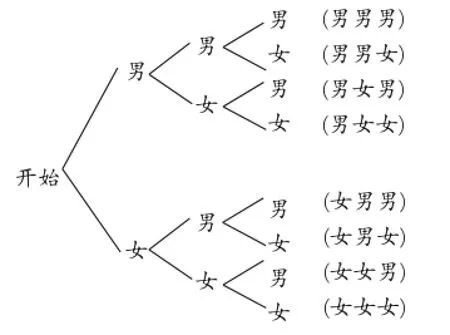
因此共有8種等可能的結果，其中1個男嬰、2個女嬰的結果數為3，所以P（1個男嬰，2個女嬰）=.

四、枚舉之法，不可忽略

平時在上課時，可能老師對列表法或樹狀圖法強調過多，同學們往往形成了思維定式，而忽略了使用這兩種方法的目的：找出試驗所有的等可能結果數以及事件發生可能出現的結果數.就如乘船過河，列表法或樹狀圖只是解題（過河）的工具（船），沒有“船”，難道我們過不了“河”嗎？

例5（2016·江蘇南京）某景區7月1日-7月7日一周天氣預報如圖，小麗打算選擇這期間的一天或兩天去該景區旅游，求下列事件的概率：

（1）隨機選擇一天，恰好天氣預報是晴；

（2）隨機選擇連續的兩天，恰好天氣預報都是晴.

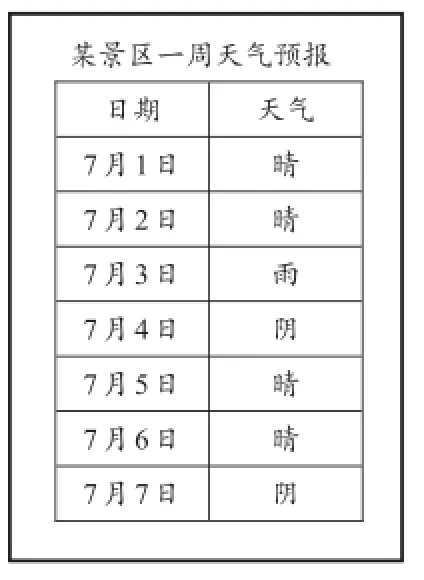
【分析】因為（2）中是選擇連續的兩天，故可以用枚舉法將所有等可能的結果列出來解答.

（作者單位：江蘇省無錫市天一實驗學校、江蘇省無錫市新城中學）