抓住例題本質(zhì)靈活解中考題

馬育偉

抓住例題本質(zhì)靈活解中考題

馬育偉

蘇科版九年級《數(shù)學(xué)》上冊第129頁有這樣一個問題.

【原題】有一個質(zhì)地均勻的正十二面體，12個面上分別寫有1～12這12個整數(shù)，投擲這個正12面體.

（1）朝上一面的數(shù)有哪些？它們發(fā)生的可能性相同嗎？

（2）朝上一面的數(shù)是奇數(shù)與朝上一面的數(shù)是偶數(shù)，發(fā)生的可能性相同嗎？

（3）朝上一面的數(shù)是4的倍數(shù)與朝上一面的數(shù)是6的倍數(shù)，發(fā)生的可能性相同嗎？

【思路點撥】投擲這個正12面體時，每個面向上是等可能的事件，因此朝上一面可能為1～12這12個整數(shù)中的某個，每個面發(fā)生的可能性是相同的.而1～12中有6個奇數(shù)和6個偶數(shù)，所以朝上一面的數(shù)是奇數(shù)與朝上一面的數(shù)是偶數(shù)發(fā)生的可能性相同，但在1～12中有3個4的倍數(shù)和2個6的倍數(shù)，因此它們發(fā)生的可能性不相同。

【自主解答】（1）朝上一面的數(shù)有1、2、3、4、5、6、7、8、9、10、11、12，它們發(fā)生的可能性相同.

（2）朝上一面的數(shù)是奇數(shù)與偶數(shù)發(fā)生的可能性相同.

（3）朝上一面的數(shù)是4的倍數(shù)與6的倍數(shù)，發(fā)生的可能性不相同.

【點評】課本中的這一問題是“中考課堂”的一個例題，即在中考考題中常常會出現(xiàn)的考題類型.概率統(tǒng)計題作為初中數(shù)學(xué)的核心內(nèi)容，要求學(xué)生充分理解事件的等可能性及發(fā)生某一事件的可能性大小求法——求概率的常用方法是先計算隨機(jī)事件發(fā)生的總可能情況數(shù)A及發(fā)生某一事件的可能情況數(shù)B，而概率的確定就是的值.

變式1（2013·福建廈門）有一個質(zhì)地均勻的正12面體，12個面上分別寫有1～12這12個整數(shù)（每個面上只有一個整數(shù)且每個面上的整數(shù)互不相同）.投擲這個正12面體一次，記事件A為“向上一面的數(shù)是2或3的整數(shù)倍”，記事件B為“向上一面的數(shù)是3的整數(shù)倍”，請你判斷等式“P（A）=+P（B）”是否成立，并說明理由.

【思路點撥】投擲這個正12面體時，每個面向上是等可能的事件，因此朝上一面可能為1～12這12個整數(shù)中的某個，而2的整數(shù)倍為2、4、6、8、10、12共6種，3的整數(shù)倍為3、6、9、12共4種，根據(jù)這一性質(zhì)易得答案.

【自主解答】不成立.

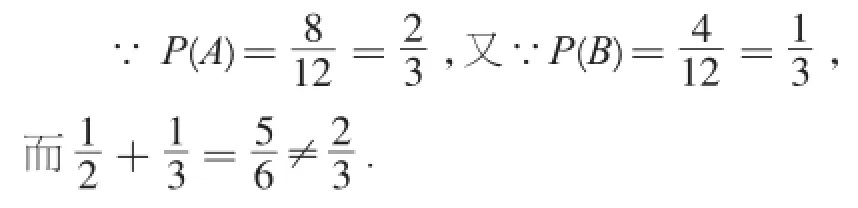
∴等式不成立.

【點評】本題的關(guān)鍵是分別求出事件A與事件B的概率，然后驗證等式是否成立.

變式2（2013·江蘇無錫）小明與甲、乙兩人一起玩“手心手背”的游戲.他們約定：如果三人中僅有一人出“手心”或“手背”，則這個人獲勝；如果三人都出“手心”或“手背”，則不分勝負(fù).那么在一個回合中，如果小明出“手心”，則他獲勝的概率是多少？（請用“畫樹狀圖”或“列表”等方法寫出分析過程）

【思路點撥】本題中雖然有三人玩“手心手背”的游戲，但已經(jīng)確定了小明出“手心”，故只需考慮甲、乙兩人出“手心”或“手背”的情況后再去分析小明獲勝的概率是多少.

【自主解答】用列表法解題如下：

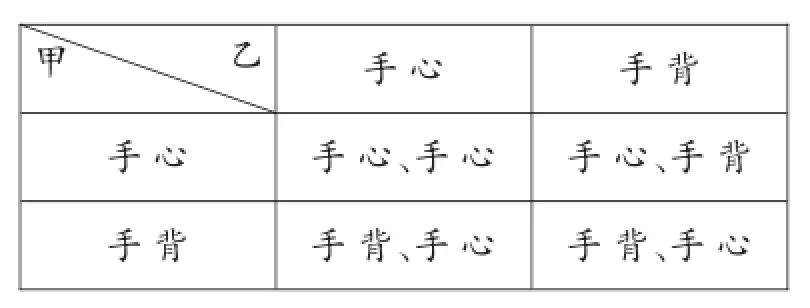
甲乙手心手背手心手心、手心手背、手心手背手心、手背手背、手心

∵小明出“手心”，甲、乙兩人出“手心”或“手背”的所有可能有4種情況，而兩人都出“手背”只有1種可能，

【點評】本題的關(guān)鍵是能分清題意，是在限定小明出“手心”的條件下的三人游戲，故不要考慮小明出“手背”的情況.

變式3（2016·江蘇無錫）甲、乙兩隊進(jìn)行打乒乓球團(tuán)體賽，比賽規(guī)則規(guī)定：兩隊之間進(jìn)行3局比賽，3局比賽必須全部打完，贏滿2局的隊為獲勝隊，假如甲、乙兩隊之間每局比賽輸贏的機(jī)會相同，且甲隊已經(jīng)贏得了第1局比賽，那么甲隊最終獲勝的概率是多少？（請用“畫樹狀圖”或“列表”等方法寫出分析過程）

【思路點撥】本題中雖然甲、乙兩隊之間進(jìn)行3局比賽，但已經(jīng)確定了甲隊贏得了第1局比賽，故只需考慮甲、乙兩隊第2、3局比賽情況后再去分析甲隊獲勝的概率是多少.

【自主解答】根據(jù)題意畫出樹狀圖如下：

一共有4種情況，確保兩局勝的有3種，

【點評】本題的關(guān)鍵是能分清題意，是已知第一局甲勝的情況下求后兩局甲獲勝情況，故不要考慮第一局甲負(fù)的情況.

（作者單位：江蘇省無錫市碩放中學(xué)）