爆炸載荷作用下大型原油儲罐動力響應分析

朱立富，閻善郁，潘科

?

爆炸載荷作用下大型原油儲罐動力響應分析

朱立富1，閻善郁2，潘科2

(1.大連交通大學 環境與化學工程學院,遼寧 大連 116028； 2.大連交通大學 土木與安全工程學院，遼寧 大連 116028)

采用ANSYS/LS-DYNA實現了碎片撞擊儲罐的有限元模擬，建立了儲罐響應的動力學模型，分析了儲罐響應的主要因素.在模擬中，依次改變碎片質量、撞擊速度、撞擊接觸面積、撞擊入射角度，討論各因素對儲罐動力響應的影響.結果表明，碎片質量、撞擊速度、撞擊入射角度與儲罐穩定性正相關，而撞擊接觸面積與之負相關.本研究創新性的提出通過改變儲罐壁材料或厚度的方法，來減少碎片撞擊儲罐的動力響應.對爆炸載荷作用下的大型原油儲罐失效預防具重大的意義.

爆炸載荷；動力響應；數值模擬；失效預防

0 引言

近年來，國內原油需求量逐年增加，儲罐及儲備庫的大型化集約化發展，雖然給國家原油儲備提供了便利，但也帶來了一些災難性事故隱患.據統計全球范圍內平均每年發生的儲罐火災爆炸事故約有 4～5起[1].其中，爆炸碎片引發的連鎖破壞是較為普遍的，且事故往往會造成非常嚴重的后果.碎片撞擊周圍的工藝設施、設備，使更多的能量意外釋放，加大事故后果嚴重性，爆炸載荷的沖擊使周圍設備設施的材料發生彈塑性變形，需要使用彈塑性相關理論對撞擊過程進行動力學響應分析[2].Park[3]等人研究了具有初動能的剛性鐵塊撞擊懸臂梁的動力響應.Hauptmanns[4- 5]預測了碎片拋射方位及各方位概率，繼而求取了周圍某一儲罐被碎片水平擊中的概率；Nguyen[6]認為當碎片撞擊儲罐的撞擊深度達到儲罐壁的厚度，或者撞擊后產生的殘余壁厚小于儲罐壁材料支撐所需厚度的臨界值時就會導致儲罐破壞泄漏事故.臨界殘余壁厚的求解涉及到復雜的局部應力分析，因而求解也具有一定困難.Mébarki[7- 8]建立了根據碎片質量、速度、碎片的撞擊面積直徑和撞擊角度求解撞擊深度的計算公式，為進一步建立碎片撞擊儲罐的破壞模型奠定了基礎.陳剛[9]考慮碎片初始的拋射高度和水平拋射位移對碎片撞擊儲罐的擊中概率的影響.本文采用ANSYS/LS-DYNA實現了碎片撞擊儲罐的有限元模擬，建立了儲罐響應的動力學模型，分析了儲罐響應的主要因素.

1 碰撞模型

ANSYS/LS-DYNA處理爆炸撞擊的算法遵循質量守恒、動量守恒、能量守恒方程[9]：

(1)屈服準則[10]

對于儲罐的材料，采用Von-Mises屈服準則，即當應力偏量第二不變量J2滿足下式時，材料發生屈服：

(1)

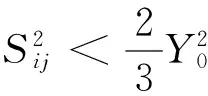
(2)材料的破壞[11]

材料的破壞準則主要考慮瞬時破壞準則和累積損傷準則.瞬時破壞準則是以靜水壓力和材料密度的斷裂臨界值ps、 ρs為基礎的，即當p≤ps,ρ≤ρs時，網格中的材料瞬時發生破壞，置p=0,Sij=0.材料破壞后，計算網格中的任何剪切應力和靜水壓力均置為零，密度不低于ρs.

2 模型模擬

在具體模擬過程中，采用ALE列式算法進行模擬分析.根據大型儲罐的儲罐壁的厚度較內徑可以視為板材的特點，本文儲罐壁的單元選用THINSHELL163 即薄殼單元.通過實參數定義薄壁厚度，為0.15 m.碎片的結構簡化為立方體，使用三維實體單元SOLID164.碎片來源于儲罐，所以儲罐和碎片的模型參數一致.本文研究的鋼材其彈性模量為2.06×1011Pa、密度為7 850 kg/m3、柏松比為0.3、屈服強度為3.25×108Pa和切線模量2.06×109Pa；原油的密度為998 kg/m3、壓力截止值-10 Pa、動力粘性系數為1.01×10-3、其余參數為0.

根據Lepareux和Neilson的實驗[11]以及本文研究的儲罐特點，確定本文研究模型基本參數入射角α：30°～70°；碎片質量mp：250～700 kg；撞擊接觸面積：0.01～0.05 m2；撞擊速度νp：40～120 m/s.

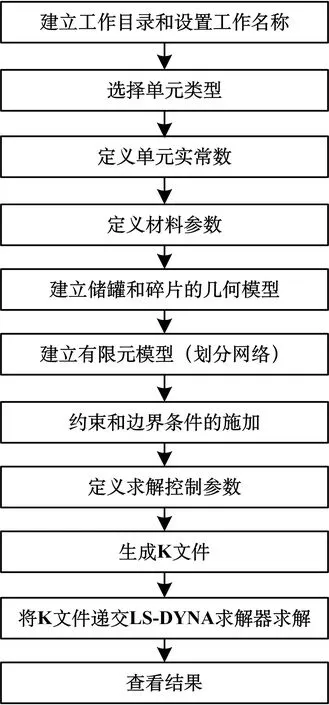
圖1 有限元模擬流程圖

模擬過程如圖1所示，首先建立工作目錄和設置工作名稱，然后進行單元類型選擇，對單元進行材料參數定義，也可在生成的K文件中進行修改.分別建立儲罐、碎片、原油幾何模型，然后對模型進行網格劃分，施加約束.定義求解時間，本文定義求解時間為25 ms.也可通過指定的節點或剛性體位移達到某一特定的位置，即當碎片X軸向距離達到15 cm時，求解結束.適用于LS-DYNA輸出的文件為二進制結果文件d3polt，可以通過lsprepost后處理軟件讀取d3plot文件，顯示模擬結果.

通過LS-DYNA求解器軟件LS-PREPOST可以顯示出模擬結果.圖2為碎片撞擊儲罐的過程圖V-M等效應力云圖.圖3(a)為碎片撞擊過程中結構的X軸方向位移云圖，從圖中我們可以看出不同單元在某一時刻的位移變化，在0.015 003這一時刻，最大位移為0.117 519 m，發生在16 376#；圖3(b)為碎片撞擊過程中結構的X軸方向加速度云圖，從圖中我們可以看出不同單元在某一時刻的加速度的變化,在0.000 994 95這一時刻，最大加速度736 947 m/s2，發生在125 434#(該單元屬于碎片)，圖中顏色的變化說明了應力、位移、加速度等參數隨時間的變化而變化.

(a)位移云圖

(b)加速度云圖

3 討論

3.1 撞擊速度的影響分析

改變碎片撞擊速度討論撞擊速度對整個過程的影響，模擬中分別以120、110、100、90、80、70、60、50、40 m/s的速度撞擊儲罐，響應結果見圖4所示.

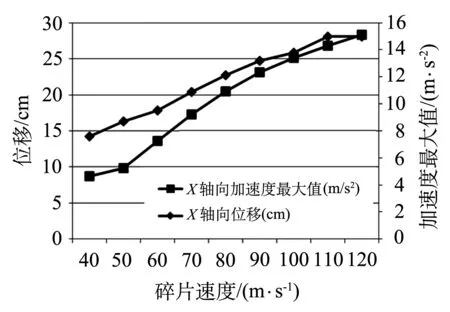
圖4 碎片速度對X軸向位移及加速度最大值的影響

圖4為在不同碎片速度撞擊下的X軸向位移、X軸向加速度最大值曲線.儲罐的X軸向位移、X軸向速度最大值隨碎片撞擊速度的增加而增加，且幅度很大，說明初始撞擊速度對撞擊效果影響很大.當撞擊速度大于110 m/s時，儲罐將被碎片擊破，進而儲罐失效.隨著初始撞擊速度的增大，碎片的動能越大，且撞擊罐體的過程中所受的罐體的抗力減小，其消耗的能量也越來越少.從圖中可以看出，撞擊速度越大，X軸向加速度最大值越大，表明那一時刻運動變化越大，破壞作用也越大，對儲罐造成的損害就越大.總之，碎片撞擊速度與儲罐動力響應成正相關，撞擊速度越大，對儲罐造成的影響越大.

3.2 碎片接觸面積的影響

改變碎片與罐體撞擊時的接觸面積，討論接觸面積對整個過程的影響.模擬中碎片撞擊儲罐的接觸面積分別為0.01、0.015、0.02、0.025、0.03、0.035、0.04、0.045、0.05 m2，響應結果見圖5所示.

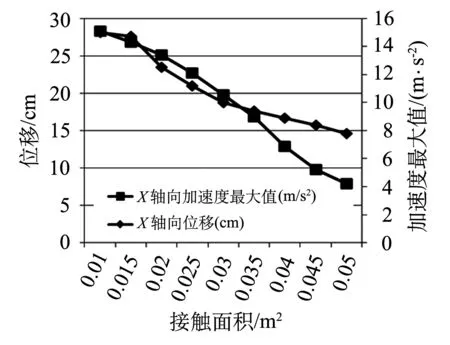
圖5 接觸面積對X軸向位移及加速度最大值的影響

圖5為在不同接觸面積撞擊下的X軸向位移和X軸向加速度最大值曲線.儲罐的X軸向位移和X軸向加速度最大值隨撞擊接觸面積的增加而減小，且幅度很大，說明接觸面積對撞擊效果影響很大.當接觸面積小于0.015 m2時，儲罐將被碎片擊破，進而儲罐失效.隨著接觸面積的增大，碎片撞擊過程中消耗的能量也就越大，撞擊罐體的過程中所受的罐體的抗力變大，X軸向位移就會變小.圖5說明，接觸面積越大，X 軸向加速度最大值越小，表明那一時刻運動變化越小，破壞作用也越小，對儲罐造成的損害就越小.總之，撞擊接觸面積與儲罐動力響應成負相關，接觸面積越小，對儲罐造成的影響越大.

3.3 碎片質量的影響

通過改變碎片質量，討論碎片質量對整個過程的影響，模擬中分別以質量為250、300、350、400、450、500、550、600、650、700 kg的碎片撞擊儲罐，碎片的質量可以可以在lsprepost中的繪圖控制區選中MAT的PLASTIC_KINEMATIC對碎片質量進行修改響應結果見圖6所示.

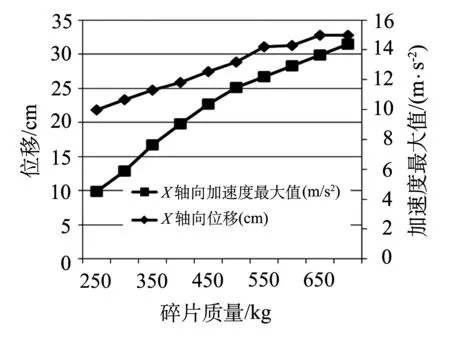
圖6 碎片質量對X軸向位移及加速度最大值的影響

圖6為不同質量的碎片撞擊下的X軸向位移和X軸向加速度最大值曲線.儲罐的X軸向位移和X軸向加速度最大值隨碎片質量的增加而增加，且幅度很大，說明碎片質量對撞擊效果影響很大.當碎片質量大于650 kg時，儲罐將被碎片擊破，進而儲罐失效.隨著碎片質量的增大，碎片的動能越大，且撞擊罐體的過程中所受的罐體的抗力減小，其消耗的能量也越來越少.圖6說明，碎片質量越大，X軸向加速度最大值越大，表明那一時刻運動變化越大，破壞作用也越大，對儲罐造成的損害就越大.總之，碎片質量與儲罐動力響應成正相關，碎片質量越大，對儲罐造成的影響越大.

3.4 碎片撞擊角度的影響

改變入射角度，討論撞擊速度對整個過程的影響.模擬中，碎片在X-Z平面內分別以與X軸方向成30°、35°、40°、45°、50°、55°、60°、65°、70°的方向撞擊儲罐.響應結果見圖7所示.

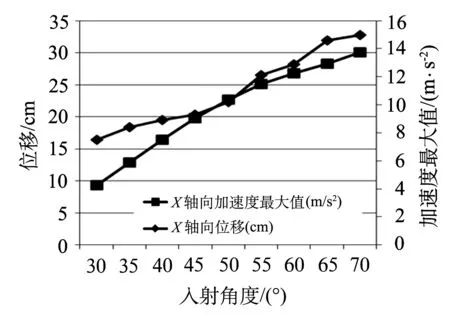
圖7 撞擊角度對X軸向位移及加速度最大值的影響

圖7為不同質量的入射角度撞擊下的X軸向位移和X軸向加速度最大值曲線.儲罐的X軸向位移和X軸向加速度最大值隨入射角度的增加而增加，且幅度很大，說明入射角度對撞擊效果影響很大.當入射角度大于65°時，儲罐將被碎片擊破，進而儲罐失效.隨著入射角度的增大，碎片的X軸方向的分動能越大，且撞擊罐體的過程中所受的罐體的抗力減小，其消耗的能量也越來越少.圖7說明，入射角度越大，X軸向加速度最大值越大，表明那一時刻運動變化越大，破壞作用也越大，對儲罐造成的損害就越大.總之，碎片入射角度與儲罐動力響應成正相關，入射角度越大，對儲罐造成的影響越大.

4 失效安全防護

從討論部分分析儲罐動力響應影響因素的結果，我們得出了碎片質量和碎片的撞擊速度越大，將導致儲罐更容易失效.可以考慮增加安全防護距離、改變儲罐罐壁、增加壁厚的方向進行分析.

4.1 選址與布置

罐區的廠址選擇與布置應符合《石油化工企業設計防火規范》所規定的區域規劃與工廠總平面布置、儲運設施、消防等的防火要求.

(1)罐區與周圍設施、建(構)筑物的安全距離：考慮周圍設施物料揮發、耐火等級、有無可燃蒸氣散發和有無明火等原因，要至少保證《石油化工企業設計防火規范》4.1.9所規定的最小防火間距[12].如居民區等八大類場所應保證的間距要大于100 m，與廠外公路應保證的間距要大于20 m，與變配電站應保證的間距要大于50 m，高架火炬應保證的間距要大于90 m，明火地點應保證的間距要大于40 m等;

(2)儲罐之間的間距：按照《石油化工企業設計防火規范》內浮頂儲罐之間的防火間距應大于0.4D(D為相鄰較大罐的直徑，單罐容積大于1 000 m3的儲罐取直徑或高度的較大值)，1 000 m3儲罐內徑：80 m，所以儲罐間距至少大于32 m.

從安全防護的角度考慮，增加碎片的飛行距離，即增加儲罐間距，碎片的撞擊速度就會減小，從圖3.1中我們得之，撞擊速度越大，對儲罐的作用效果越明顯，如速度從110 m/s，減低至100 m/s，X軸向位移將減少0.98 cm、X軸向加速度最大值將減少1.7 m/s2.所以增大儲罐間距，可盡可能的減少對儲罐的損害.

4.2 罐壁材料選擇

罐壁的材料不同，屈服強度也不同.本文將通過對比Q235、Q325、Q345三種不同鋼材，對不同材料的撞擊模擬.更改屈服強度可以在lsprepost中的繪圖控制區選中對儲罐的屈服強度進行修改.得出不同材料的X軸位移圖如圖8.

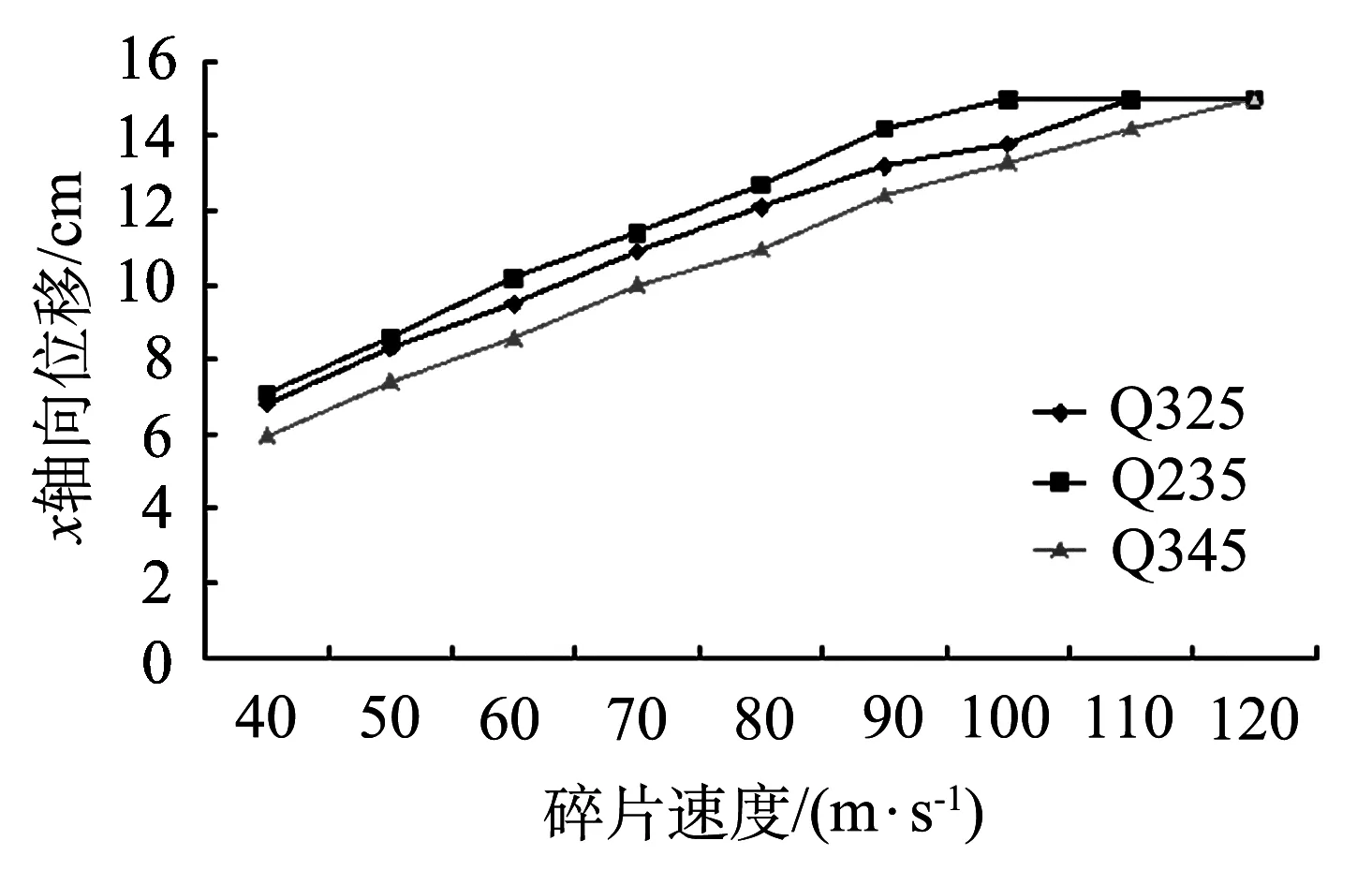
圖8 三種不同鋼材材料的對比圖

從圖中可以看出，我們可以選擇屈服強度更大的材料作為罐壁，將有效的降低儲罐的影響.

4.3 壁厚分析

HyPerworks是一個對有限元結構分析與優化的軟件.它可以對象進行拓撲優化、形貌優化、尺寸優化、形狀優化以及目有尺寸和自由形狀優化技術.應用拓撲，可以對尺寸和形狀優化，因此可以計算出避免已知約束力作用下儲罐失效，儲罐應該達到最小的厚度.

在圖4中，我們可以發現當碎片速度達到120 m/s，儲罐被擊破，因此本文的優化目標為：依然是速度依然是120 m/s時，儲罐不被擊破，儲罐壁應達到的厚度.

通過lsprepost讀取出碎片在120 m/s產生的最大撞擊力為5.53×109N，該力為約束條件.然后在OPtistruct中，載入在ANSYS中建立的模型.

在OPtistruct中，需重新定義儲罐的材料等參數，然后定義響應區域，本文為儲罐壁.然后定義目標函數，本文選取的目標函數為響應區域質量最小，因為儲罐壁的厚度，決定著儲罐壁的整個體積，進而決定著質量.定義約束包括地面的約束以及撞擊力及以及各自的約束位置等.保存HyPerworks數據文件后，進行運行.在輸出文件中查看結構分析結果.從圖9中，我們可以讀出，為了避免120 m/s的碎片撞擊儲罐，儲罐不被穿破的最小距離為158.6 mm.因此，在儲罐設計上，可以通過增加儲罐壁厚度，減小碎片撞擊對儲罐結構的影響.

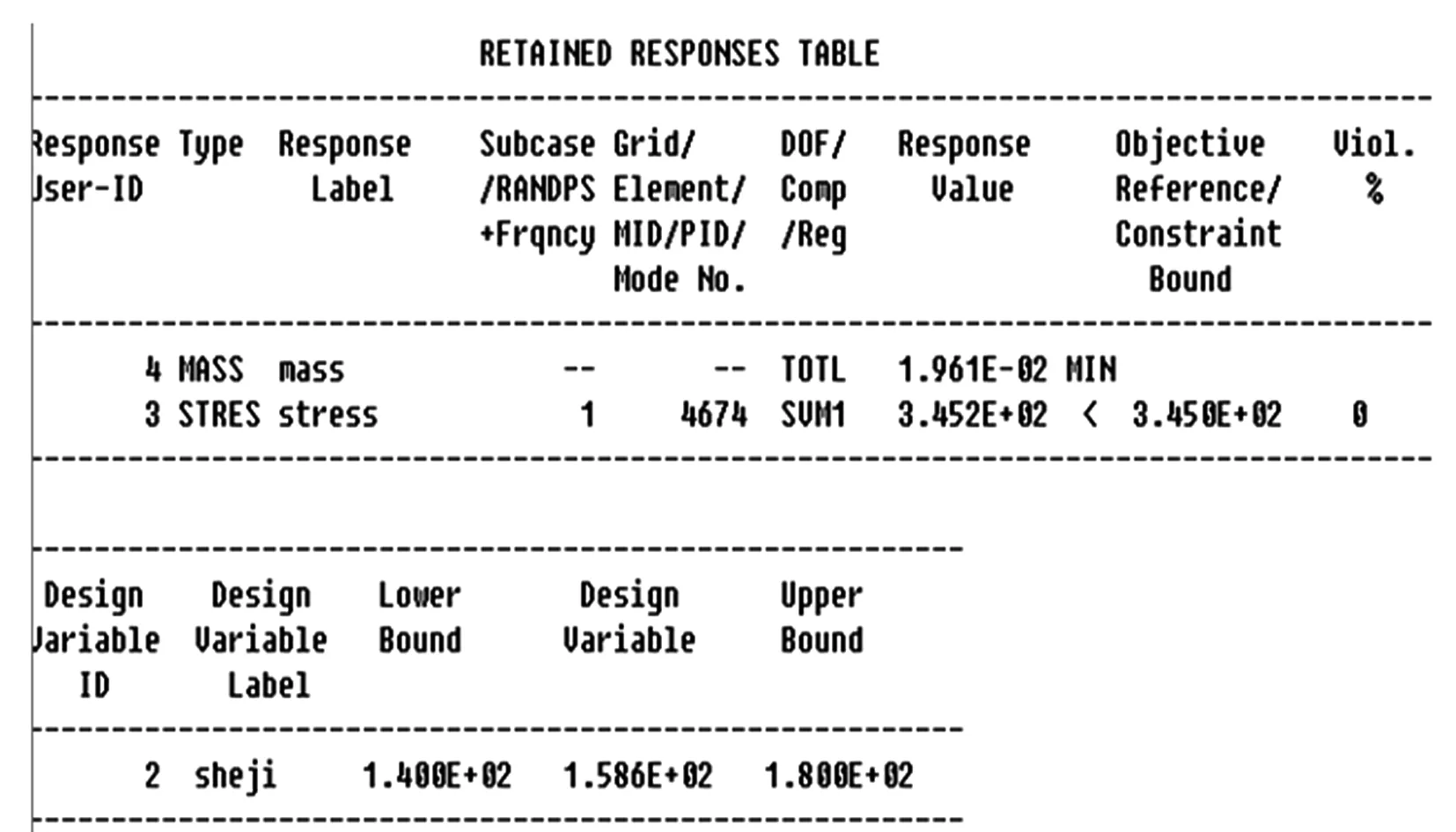
圖9 輸出文件

5 結論

基于以上的分析與研究，得出以下主要：

(1)碎片質量越大、碎片速度越大、碎片撞擊儲罐接觸面積越小、撞擊入射角度越大、儲罐變得越來越不穩定，儲罐越容易失效，撞擊損害程度與碎片質量、碎片速度、撞擊入射角度成近似正比的關系，與碎片撞擊儲罐接觸面積成近似正比的關系；

(2)碎片質量大于650 kg、或碎片速度大于110 m/s，或碎片接觸面積小于0.015 m2、碎片入射角度大于65°時，儲罐會被擊穿，造成泄漏；

(3)通過模擬對比，驗證了屈服強度越大的材料越能減小儲罐的動力響應；通過對儲罐壁厚的優化，可以得到預防不同嚴重程度的撞擊，儲罐不被擊穿的最小厚度.

[1]陳剛，朱霽平，武軍，等.化工儲罐間距和體積對爆炸碎片多米諾效應概率的影響[J].火災科學,2011,20(1)：1- 6.

[2]韓強.彈塑性系統的動力屈曲和分叉[M].北京:科學出版社,2000.

[3]PARK E W.The permanent deformation of a cantilever struck transversely at its tip[J].Pro R Soc,1955,A228:462- 476.

[4]HAUPTMANNS U.A Monte Carlo-based procedure for treating the flight of missiles from tank explosions[J].Probabilistic Engineering Mechanics,2001,16(4)：307- 312.

[5]HAUPTMANNS U.A procedure for analyzing the flight of missiles from explosions of cylindrical vessels[J].Journal of Loss Prevention in the Process Industries，2001,14(5):395- 402.

[6]NGUYEN Q B,MEBARKI A,AMI R,et al.Integrated probabilistic framework for domino effect and risk analysis[J].Advances in Engineering Software，2009,40:892- 901.

[7]MéBARKI A，NGUYEN Q B，MERCIER F，et al.Aprobabilistic model for the vulnerability of metal plates under the impact of cylindrical projectiles[J].Journal of Loss Prevention in the Process Industries,2007,20(2):128- 134.

[8]MéBARKI A， NGUYEN QB，MERCIER F，et al.Reliability analysis of metallic targets under metallic rods impact:towards a simplified probabilistic approach[J].Journal of Loss Prevention in the Process Industries，2008,21(5):518- 527.

[9]白金澤.LS-DYNA3D理論基礎與實例分析[M].北京:科學出版社,2005.

[10]MIKALSEN R,ROSKILLY A P.Performance simulation of a spark ignited free-piston engine generator[J].Applied Thermal Engineering,2008,28(5- 6):1726- 1733.

[11]寧建國.爆炸與沖擊動力學[M].北京：國防工業出版社,2010.

[12]中國石油化工總公司.GB 50160- 2008石油化工企業設計防火規范[S].北京：中國計劃出版社，2008.

Study of Dynamic Response of Large-Scale Tank under Blast Loads

ZHU Lifu1,YAN Shanyu2,PAN Ke2

(1.School of Environmental and Chemical Engineering,Dalian Jiaotong University，Dalian 116028,China； 2.School of Civil & Safety Engineering，Dalian Jiaotong University，Dalian 116028,China)

Finite element method is performed to simulate explosion fragments hitting storage tank by ANSYS/LS-DYNA.The dynamic model is built,and the main factors of tank response are analyzed. In simulation,some factors are changed to analyzed the response to the tank,including the explosion fragments of the mass,velocity,contact area and angle in the impact.Except that the contact area is a negative correlation with the stability of the storage tank,other factors are positive correlation. It is firstly indicated that the fragments impact response of the storage tank is decreased by the change in material and/or thickness of the tank wall,suggesting that it is significant to prevent the failure of the oil storage tank under explosion.

explosive load;dynamic response;numerical simulation;failure prevention

1673- 9590(2016)02- 0082- 06

2015- 04- 07

朱立富(1988-),男，碩士研究生；閻善郁(1955-)，男，教授,碩士，主要從事環境安全控制與評價的研究E-mail:zhulifu2013@163.com.

A