基于自適應競爭群優化算法的無分流換熱網絡綜合

陳帥，羅娜

?

基于自適應競爭群優化算法的無分流換熱網絡綜合

陳帥，羅娜

（華東理工大學化工過程先進控制與優化技術教育部重點實驗室，上海 200237）

換熱網絡模型具有非凸和非線性的特性，對于大規模超結構優化問題，采用經典的智能算法優化效率低，容易陷入局部最優值。以年綜合費用為目標函數，基于自適應競爭群優化算法對無分流分級超結構換熱網絡模型進行優化。該方法采用對粒子平均位置的遞減學習，通過自適應調節速度權重提高換熱網絡結構的全局優化能力和局部優化能力。通過兩個典型算例分析表明，該方法相比量子粒子群算法大幅減少了模型調用次數，縮短了運行時間，并且找到了更好的優化結果。

換熱網絡；優化；自適應；競爭群優化算法；混合整數非線性

引 言

換熱網絡作為過程工業的重要部分，實現換熱網絡流股間的最佳換熱匹配，能有效回收熱量，減少能量的浪費。Linnhoff等[1]于1978年通過夾點分析法求解換熱網絡。經過多年的發展，1990年Yee等[2]提出了分級超結構概念，該概念的提出使得換熱網絡優化有了新的突破。

近年來，如何有效求解換熱網絡綜合，減少能量的消耗，一直都是研究的重點。換熱網絡存在連續和離散變量，Athier等[3]采用分層求解的方式來解決。以二次規劃法求解NLP問題，再通過模擬退火算法對溫度及熱負荷等連續變量進行優化，解決了連續變量和離散變量同時存在的難題。Zamora等[4]采用分支界定法分析無分流換熱網絡變量邊界關系改進估計函數，通過外圍逼近法優化換熱網絡結構，該方法計算簡單易行。Dipama等[5]提出設置無分流換熱網絡匹配矩陣，減少了優化變量個數，通過遺傳算法對無分流換熱網絡綜合進行優化，提高了優化效率。Bjork等[6]提出設定熱容流率和傳熱系數為定值時，換熱網絡進行等溫混合的超結構模型，該方法解決了大規模換熱網絡優化問題。Khorasany等[7]將和聲算法應用于換熱網絡流股匹配選擇，通過二次規劃法換熱量和分流比進行連續優化，為雙層算法求解問題提供了新方法。夏濤等[8]采用粒子群算法求解速度快的特點，將約束條件和投資費用同時考慮在無分流換熱網絡模型中進行求解，有效處理了換熱約束問題。Soltani等[9]采用帶壓力降的遺傳算法結合線性規劃法優化無分流換熱網絡，減少了模型的復雜度。霍兆義等[10]提出遺傳算法進行流股二進制編碼優化換熱網絡結構,通過改進的粒子群算法優化熱負荷和分流比等連續變量的雙層算法。趙亮等[11]以遺傳算法的優化特點對換熱網絡流股進行二進制編碼處理，通過雙層粒子群算法對無分流換熱網絡進行優化。無分流換熱網絡結構相比有分流換熱網絡結構簡單，對于求解變量大規模換熱網絡，雙層算法解決有分流換熱網絡所需的成本較高。

無分流換熱網絡結構相比于有分流換熱網絡結構不考慮流股的分流比，減少了需要優化的變量數目，使優化的換熱網絡模型簡化。雙層算法優化時，使目標函數調用次數大大增加，對于大規模優化問題，計算效率不高。本文以無分流換熱網絡年綜合費用評價算法的優化效果，采用單層自適應競爭群優化算法(adaptive competitive swarm optimization, ACSO)對無分流換熱網絡進行求解，以期提高換熱網絡問題求解的優化效率，得到更好的優化結果。

1 無分流換熱網絡數學模型

1.1 分級超結構模型

無分流超結構換熱網絡模型，如圖1所示。該模型被劃分為兩級，每一級中有H×C種可能匹配，其中H代表模型熱流股個數，C代表模型冷流股個數。通過冷熱流股間的匹配，回收流股間的熱量，對于未達到目標溫度的冷熱流股采用公用工程對流股進行加熱或冷卻以達到目標值。

本文以無分流超結構換熱網絡的最小年綜合費用作為優化目標。換熱網絡的年綜合費用由流股末端加熱冷卻時產生的公用工程的費用和設備的固定投資費用及流股換熱時換熱面積的費用組成，如式(1)所示。

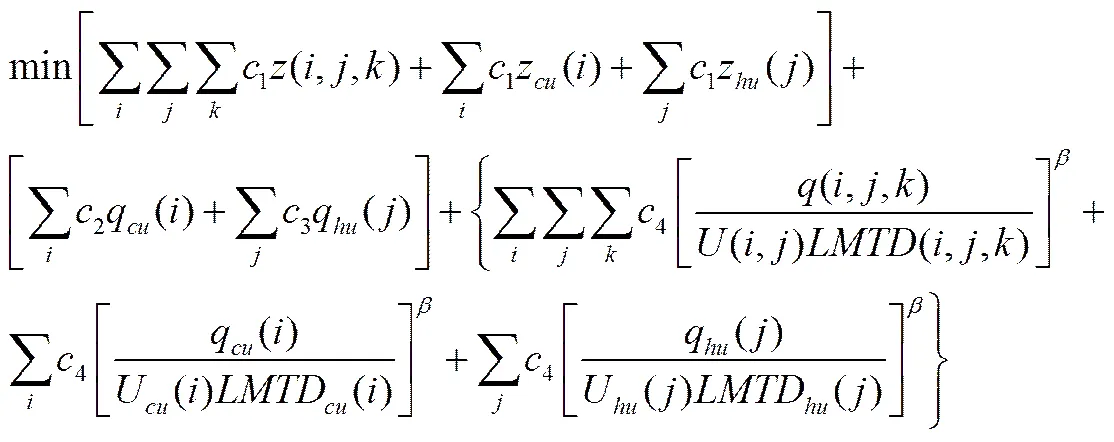
(2)

(3)

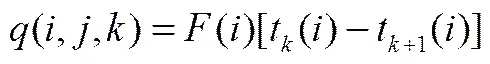
式(1)中，第1部分為換熱網絡固定投資的費用，1代表換熱網絡設備固定投資的費用系數，代表換熱器存在與否的數值；第2部分為流股末端公用工程產生的費用，2和3分別為冷熱公用工程產生的費用系數；第3部分為換熱網絡的換熱面積所需費用，4代表換熱面積所需的費用系數，，，分別代表冷熱流股的位置和換熱網絡級數的位置；和代表冷熱公用工程；代表換熱時的換熱量；代表換熱網絡的總傳熱系數，代表流股的對數平均溫差，代表設備的換熱面積指數。式(2)～式(4)分別代表冷公用工程負荷、熱公用工程負荷和換熱器熱負荷。代表流股的熱容流率，代表換熱網絡的總級數，代表換熱器的進出口溫度。

約束條件

（1）每條流股的總熱平衡

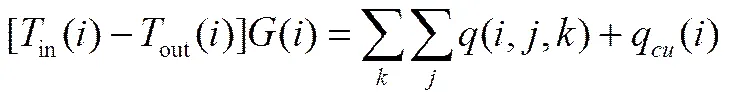
(6)

式(5)～式(6)中，in()、in()分別代表熱流股及冷流股的換熱網絡入口溫度；out()、out()分別代表熱流股及冷流股的換熱網絡出口溫度；()、()分別代表熱流股及冷流股的熱容流率。

（2）每級的熱平衡

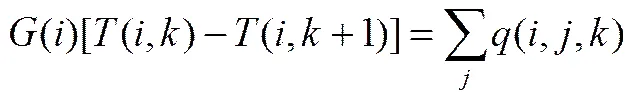
(8)

式(7)～式(8)中，()、()分別代表每級冷熱流股的入口溫度。

（3）流股溫度約束

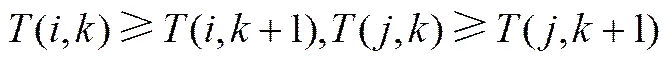
(10)

（4）溫差約束

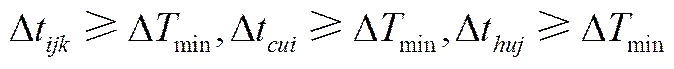
(12)

式(11)～式(12)中，Dt、Dt、Dt分別代表換熱網絡的換熱器、冷卻器及加熱器的換熱溫差，Dmin代表換熱網絡的最小傳熱溫差。()、q()、q()分別代表冷熱流股進行匹配換熱時的換熱量及冷熱公用工程負荷。

2 換熱網絡求解方法

2.1 智能群優化算法

2.1.1 粒子群算法 粒子群算法（particle swarm optimization, PSO）是Kennedy等[12]在1995年提出的，通過粒子對當前最優值信息和全局最優值信息進行學習的智能算法。算法對于簡單模型求解，具有收斂速度快、結果好的特點。對于速度權重線性遞減的粒子，具有更強的局部搜索能力。但對于復雜模型優化，粒子群算法容易過早收斂，陷入局部最優值較難跳出。速度權重遞減的粒子群算法(improved particle swarm optimization, IPSO)的速度權重如式(13)所示。

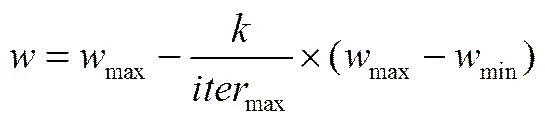
2.1.2 競爭群優化算法 Jin等[13]根據粒子群算法的學習機制于2015年提出不帶記憶信息學習的競爭群優化算法(competitive swarm optimization, CSO)。算法在群體間引入競爭機制，將粒子隨機等分成兩組采用兩組間的粒子隨機選擇競爭，通過目標函數評價使獲勝的粒子保留至下一代，失敗的粒子通過學習獲勝的粒子進行更新傳遞到下一代。每個粒子等機率的選擇競爭方式及不帶信息的學習方式，使得陷入局部最優的可能性降低。CSO的更新策略如下

(14)

其中，X,k()，X,k()和V,k()，V,k()代表第次競爭獲勝粒子和失敗粒子的位置信息和速度信息。1(,)、2(,)、3(,)是范圍[0，1]的3個隨機數。是第次競爭粒子的平均值。是控制對粒子更新的影響大小的參數。

2.2 自適應競爭群優化算法

PSO算法和CSO算法都通過粒子與粒子間相互學習進化，從而不斷接近全局最優值的方式進行更新。對于大規模復雜模型優化，基于速度權重線性遞減的PSO算法依賴最優值的信息，容易陷入局部最優。而ACSO算法不帶記憶信息學習，通過對粒子平均位置的遞減學習，隨著搜索能力的變化，當達到設置的搜索能力臨界時，自適應調節速度權重以加強局部搜索能力，調節后的速度權重隨著迭代次數的增加線性遞減。

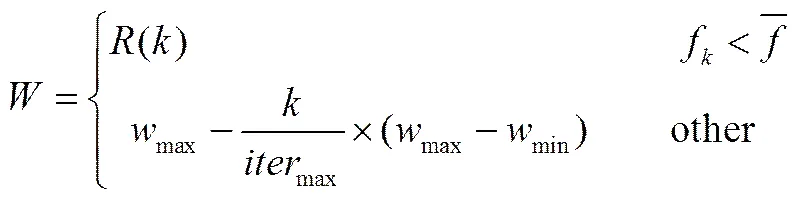
其中，()為[0,1]的隨機數，max為最大慣性值取0.9，min為最小慣性值取0.4，為進化代數，f為當前最優目標函數值，為連續20代平均年綜合費用。搜索初期粒子處于隨機較分散的空間，競爭粒子的平均值提供更多的學習信息，加強對粒子間平均位置的學習，對平均位置權重值進行遞減學習，有效提高了算法的收斂性。的取值在算例中給出，改進后的公式為

(17)

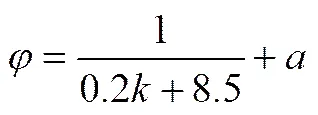
ACSO流程圖如圖2所示。

圖2 ACSO算法流程

Fig.2 ACSO algorithm procedure

自適應競爭群優化算法對無分流換熱網絡的求解步驟如下。

（1）初始化ACSO算法種群規模，最大迭代次數，換熱網絡流股參數和2個變量。

（2）前個變量代表換熱網絡模型的結構變量，以0～1之間的連續變量判斷是否存在換熱網絡匹配情況，最大的變量值判斷換熱器存在。后個變量代表計算熱負荷的中間變量。

（3）將變量代入模型進行結構調整，根據式(19)計算熱負荷。熱負荷及冷熱流股溫度從左往右進行計算，當冷流股的溫度不符合給定的入口溫度將溫度進行向右平移調整，保證換熱負荷的值不變，計算年綜合費用。

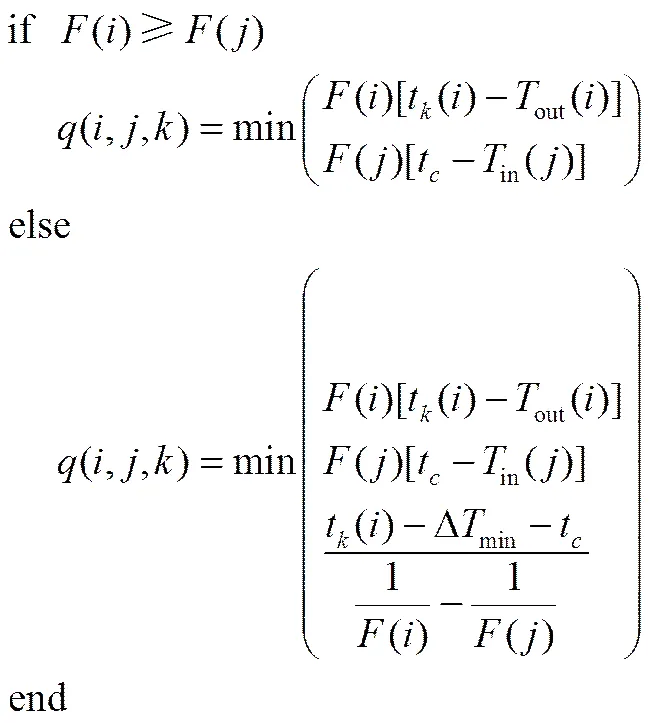
（4）采用算法的競爭機制，以年綜合費用較小的粒子為獲勝粒子，保留至下一代不參與調用模型。失敗的/2個粒子進行學習更新。

（5）算法更新時，粒子對平均位置進行遞減學習，當學習能力降低，根據式(16)調節速度權重，提高算法的局部搜索能力。

（6）輸出最優的粒子及最小年綜合費用。

3 算例分析

文中此部分工作均通過Matlab2014a進行編程，在Windows7系統下開展。采用的計算機配置為Inter Core i5 CPU@2.67GHz，4GB內存。

算例1取自文獻[14-17]。分析的算例中包含10條熱流股、10條冷流股、1條熱公用工程流股和1條冷公用工程流股，最小傳熱溫差取10 K。流股參數如表1所示。優化算法中取0.25，ACSO對換熱網絡進行優化后的結果如表2所示。

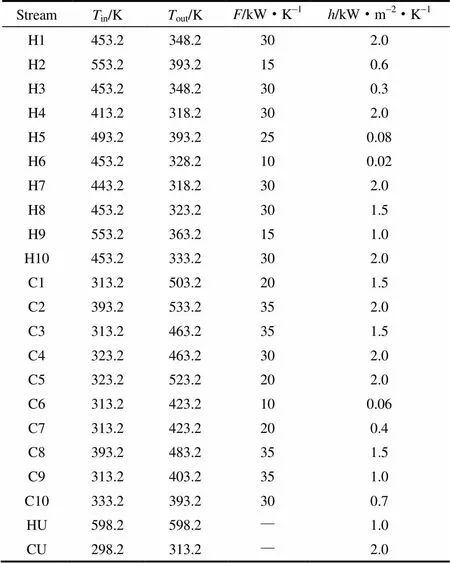
表1 算例1的物流數據

Note: cost of heat exchanger=(8000+8000.8)USD; hot utility cost= 70 USD·kW-1·a-1; cold utility cost=10 USD·kW-1·a-1.

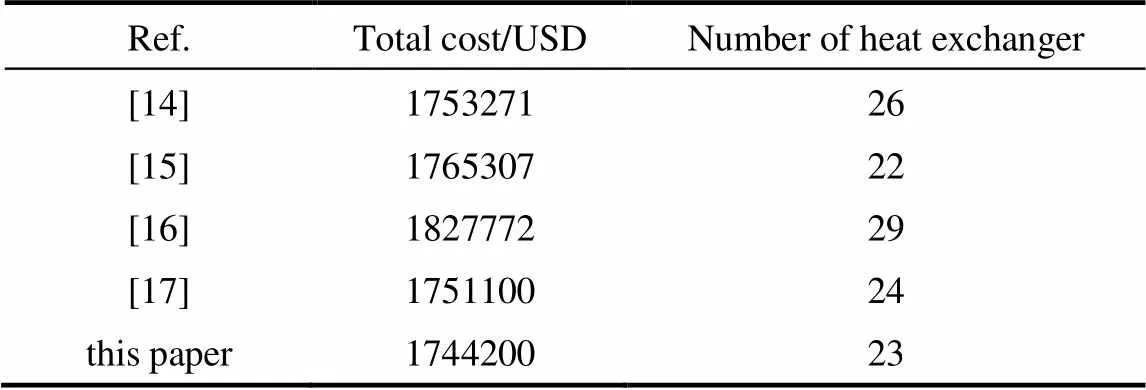
表2 算例1優化結果比較

由表2可知，文獻[14]采用混合遺傳算法結合局部優化和結構控制策略優化換熱網絡，優化后的年綜合費用為1753271 USD。文獻[15]采用遺傳算法進行流股二進制編碼優化換熱網絡結構，通過粒子群算法優化熱負荷和分流比等連續變量的雙層算法，優化后的年綜合費用為1765307 USD。文獻[16]采用遺傳算法對換熱網絡結構進行編碼優化，通過模擬退火算法對有分流換熱網絡的熱負荷及分流比等連續變量進行求解，優化后的年綜合費用為1827772 USD。文獻[17]采用狼群算法和量子粒子群算法(quantum particle swarm optimization, QPSO)結合的改進算法對無分流換熱網絡進行優化，優化后的年綜合費用為1751100 USD。

通過文獻[14-17]可知，有分流換熱網絡模型優化相比無分流換熱網絡模型優化，計算更加復雜。從優化后的結果可知換熱網絡設備單元相差0～4個，存在有分流的結構并不多，無分流換熱網絡結構簡單，對規模越大的換熱網絡進行結構優化，所需的計算成本更低。

算例1通過自適應競爭群優化算法優化無分流換熱網絡結構如圖3所示，圖4為自適應競爭群優化算法、競爭群優化算法和速度權重遞減的粒子群算法對算例1的優化后得到的無分流換熱網絡年綜合費用的收斂曲線。由圖4可知，ACSO算法相比CSO算法提高了收斂速度和優化值，ACSO算法相比IPSO有更好的優化值。

算例2取自文獻[18-21]，分析的算例中包含8條熱流股、7條冷流股、1條熱公用工程流股和1條冷公用工程流股，最小傳熱溫差取10 K。流股參數如表3所示。優化算法的值取0.14，ACSO對換熱網絡進行優化后的結果如表4所示。

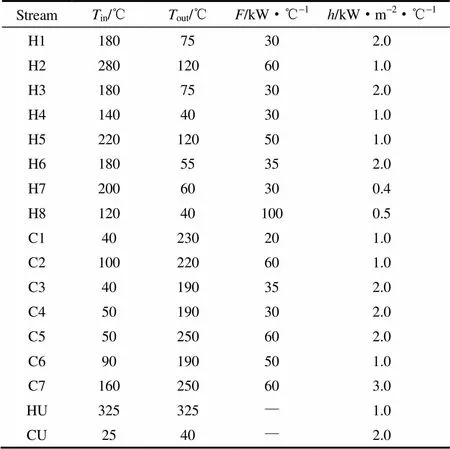
表3 算例2的物流數據

Note: cost of heat exchanger=(8000+5000.75)USD; hot utility cost=80 USD·kW-1·a-1; cold utility cost=10 USD·kW-1·a-1.

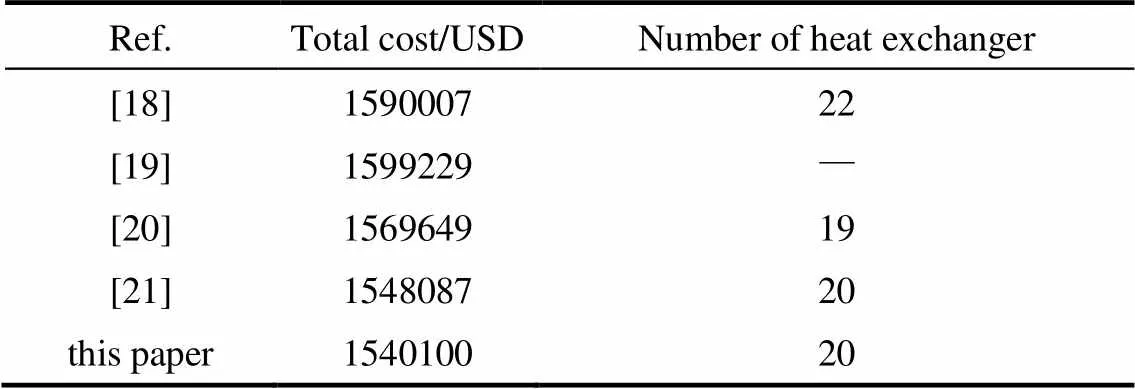
表4 算例2優化結果比較

由表4可知，文獻[18]采用填充函數法構造輔助函數，通過不斷地迭代，使目標函數容易跳出局部最優解，優化后的年綜合費用為1590007 USD。文獻[19]采用遺傳算法結合確定性算法改進換熱網絡結構，優化后獲得的年綜合費用為1599229 USD。文獻[20]通過蒙特卡羅方法對無分流換熱網絡結構進行流股匹配優化，然后采用遺傳算法對換熱網絡的換熱量等連續變量進行優化，最終得到優化后的年綜合費用為1569649 USD。文獻[21]采用蟻群算法對無分流換熱網絡進行優化，最終得到的網絡結構由20個換熱單元組成，年綜合費用為1548087 USD。

算例2通過自適應競爭群優化算法優化后的無分流換熱網絡結構如圖5所示，圖6為自適應競爭群優化算法、競爭群優化算法和速度權重遞減的粒子群算法對算例2的優化后的無分流換熱網絡年綜合費用的收斂曲線。由圖6可知，ACSO算法相比CSO算法和IPSO算法具有更好收斂速度和優化值。

本文采用基于自適應競爭群優化算法，通過對粒子平均位置遞減學習的競爭群優化算法進行換熱網絡結構全局尋優，隨著迭代學習對模型搜索能力下降達到臨界值，自適應調節為線性遞減速度。該方法提升了算法的尋優能力。相比雙層算法，優化效率更高，相比于單層換熱網絡優化，調用目標函數次數也更少，在優化效率上有較好的表現。對比文獻中的年綜合費用，算例1和算例2的優化結果更優。

效率分析：以文獻[17]的單層QPSO為例。圖7表示在算例1中，粒子種群取400，最大迭代次數500次的條件下，QPSO算法和ACSO算法運行10次取平均值進行的效率比較。圖中ACSO算法調用模型次數10萬次，平均運行時間634s，相比QPSO算法調用次數減少了50%及程序的運行時間減少了52%。

圖8中表示在算例2中，粒子種群取400，最大迭代次數500次的條件下QPSO算法和ACSO算法進行效率比較，圖中ACSO算法調用模型次數10萬次，平均運行時間383 s，相比QPSO算法模型調用次數減少了50%及程序運行時間減少了50%。

4 結 論

本文對大規模的超結構無分流換熱網絡優化進行研究，針對優化復雜模型調用模型次數較多，算法過早收斂，求解效率較低，提出了ACSO算法。CSO算法的競爭學習機制降低了粒子更新次數，對于平均位置的遞減學習提高了優化效率，自適應調節速度權重有助于局部深度優化。在以上兩個無分流典型算例中，減少了50%模型調用次數，縮短了50%左右的運行時間，取得了更好的優化結果，對于求解大規模換熱網絡有較好的效果。驗證了本文所提出算法的有效性。

References

[1] LINNHOFF B, FLOWER J R. Synthesis of heat exchanger networks（I）：Systematic generation of energy optimal networks[J]. AIChE Journal, 1978, 24(4): 633-642.

[2] YEE T F, GROSSMANN I E. Simultaneous optimization models for heat integration(Ⅱ)：Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1184.

[3] ATHIER G, FLOQUET P, PIBOULEAU L,. Synthesis of heat-exchanger network by simulated annealing and NLP procedures[J]. AIChE Journal, 1997, 43(11): 3007-3020.

[4] ZAMORA J M, GROSSMANN I E. A global MINLP optimization algorithm for the synthesis of heat exchanger networks with no stream splits[J]. Computers & Chemical Engineering, 1998, 22(3): 367-384.

[5] DIPAMA J, TEYSSEDOU A, SORIN M. Synthesis of heat exchanger networks using genetic algorithms[J]. Applied Thermal Engineering, 2008, 28(14/15): 1763-1773.

[6] BJORK K M, WESTERLUND T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption[J]. Computers & Chemical Engineering, 2002, 26(11): 1581-1593.

[7] KHORASANY R M, FESANGHARY M. A novel approach for synthesis of cost-optimal heat exchanger networks[J]. Computers & Chemical Engineering, 2009, 33(8): 1363-1370.

[8] 賈濤, 夏濤. 常減壓蒸餾過程換熱網絡的粒子群優化設計方法[J]. 計算機與應用化學, 2009, 26(11): 1509-1514.JIA T, XIA T. An intelligent approach for designing heat exchanger network in atmospheric and vacuum distillationparticle swarm optimization[J]. Computers & Applied Chemistry, 2009, 26(11): 1509-1514.

[9] SOLTANI H, SHAFIEI S. Heat exchanger networks retrofit with considering pressure drop by coupling genetic algorithm with lp (linear programming) and ILP (integer linear programming) methods[J]. Fuel & Energy Abstracts, 2011, 36(36): 2381-2391.

[10] 霍兆義, 趙亮, 尹洪超, 等. 基于群體智能算法的換熱網絡同步最優綜合[J]. 化工學報, 2012, 63(4): 1116-1123.HUO Z Y, ZHAO L, YIN H C,. A hybrid swarm intelligence algorithm for simultaneous synthesis of heat exchanger network[J]. CIESC Journal, 2012, 63(4): 1116-1123.

[11] 趙亮, 霍兆義, 李棟斌, 等. 無分流換熱網絡同步優化綜合[J]. 熱科學與技術, 2013, 12(1): 68-73. ZHAO L, HUO Z Y, LI D B,. Simultaneous synthesis of heat exchanger network with no split streams[J]. Journal of Thermal Science & Technology, 2013, 12(1): 68-73.

[12] KENNEDY J, EBERHART R. Particle swarm optimization//1995 IEEE International Conference on Neural Networks Proceedings[C]. Perth: IEEE, 1995: 1942-1948.

[13] RAN C, JIN Y C. A competitive swarm optimizer for large scale optimization[J]. IEEE Transactions on Cybernetics, 2015, 45(2): 191-204.

[14] LUO X, WEN Q Y, FIEG G. A hybrid genetic algorithm for synthesis of heat exchanger networks[J]. Computers & Chemical Engineering, 2009, 33(6): 1169-1181.

[15] 霍兆義, 尹洪超, 趙亮. 有分流換熱網絡同步綜合[J]. 大連理工大學學報, 2013, 53(1): 45-50. HUO Z Y, YIN H C, ZHAO L. Simultaneous synthesis of heat exchanger network with stream splits[J].Journal of Dalian University of Technology, 2013, 53(1): 45-50.

[16] 肖武. 基于流股有效溫位的大規模多流股換熱器網絡綜合[D]. 大連：大連理工大學, 2006. XIAO W. Large scale multi-stream heat exchanger network synthesis based on the stream effective temperature level[D]. Dalian: Dalian University of Technology, 2006.

[17] 葉貞成, 錢智媛, 羅娜. 基于改進量子粒子群算法的無分流換熱網絡綜合[J]. 華東理工大學學報, 2015, 41(2): 166-172. YE Z C, QIAN Z Y, LUO N. Simultaneous synthesis of heat exchanger network with no split streams based on improved quantum particle swarm algorithm[J]. Journal of East China University of Science and Technology, 2015, 41(2): 166-172.

[18] 胡向柏, 崔國民, 涂惟民, 等. 換熱網絡填充函數法的全局優化[J]. 化學工程, 2011, 39(1): 28-31.HU X B, CUI G M, TU W M,. Global optimization of filled function method for heat exchanger networks[J]. Chemical Engineering (China), 2011, 39(1): 28-31.

[19] BJORK K M, NORDMAN R. Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J]. Chemical Engineering & Processing, 2005, 44(8): 869-876.

[20] 張勤, 崔國民, 關欣. 基于蒙特卡羅遺傳算法的換熱網絡優化問題[J]. 石油機械, 2007, 35(05): 19-22. ZHANG Q, CUI G M, GUAN X. Optimization of heat exchanger network based on Monte Carlo genetic algorithm[J]. CPM, 2007, 35(5): 19-22.

[21] 萬義群, 崔國民. 蟻群算法在換熱網絡優化中的應用[J]. 能源研究與信息, 2013, 29(4): 234-238. WAN Y Q, CUI G M. Application of ant colony algorithm in optimization of heat exchanger networks[J].Energy Research & Information, 2013, 29(4): 234-238.

Adaptive competitive swarm optimization for heat exchanger networks without split streams

CHEN Shuai, LUO Na

(Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China)

For large-scale super-structure optimization on non-convex and non-linear heat exchanger network, conventional intelligent optimization algorithms have poor efficiency and easily fall into local optima. Adaptive competitive swarm optimization algorithm was proposed to optimize no-split stream heat exchanger networks with targeted total annual cost. This method improved abilities of both global and local optimization by attenuated learning of average particle positions and self-adaptive adjusting on weight average of speed. Simulation on two typical cases showed that the proposed algorithm sharply reduced cycles of model being used, shortened optimization time and achieved better optimization results in comparison with quantum particle swarm algorithm.

heat exchanger network; optimization; adaptive; competitive swarm optimization; MINLP

2016-05-03.

LUO Na, naluo@ecust.edu.cn

10.11949/j.issn.0438-1157.20160581

TQ 021.8

A

0438—1157（2016）11—4716—08

陳帥(1990—)，男，碩士研究生。

國家自然科學基金項目(61403140，21406064)；上海市自然科學基金項目(13ZR1411500，14ZR1410500)。

2016-05-03收到初稿，2016-08-03收到修改稿。

聯系人：羅娜。

supported by the National Natural Science Foundation of China (61403140, 21406064) and the Natural Science Foundation of Shanghai(13ZR1411500, 14ZR1410500).