基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演
白 璐, 韓立國(guó), 張 盼, 胡 勇
(吉林大學(xué) 地球探測(cè)科學(xué)與技術(shù)學(xué)院,長(zhǎng)春 130011)
?
基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演
白 璐, 韓立國(guó), 張 盼, 胡 勇
(吉林大學(xué) 地球探測(cè)科學(xué)與技術(shù)學(xué)院,長(zhǎng)春 130011)
常規(guī)的全波形反演對(duì)初始模型和低頻數(shù)據(jù)的依賴(lài)性較強(qiáng),反演精確度經(jīng)常會(huì)受到“跳周”現(xiàn)象的嚴(yán)重影響。將小波域最小平方濾波引入到全波形反演中,并利用小波變換的多尺度特性,有效地提高了反演過(guò)程的穩(wěn)定性,減小反演受到“跳周”現(xiàn)象影響的可能性。小波域最小平方濾波具有更高的精度和更好的性能,利用該算法調(diào)整模擬波場(chǎng)的相位,從而改善模擬波場(chǎng)和觀測(cè)波場(chǎng)之間的相位差異,并由此構(gòu)造一個(gè)新的目標(biāo)函數(shù)。同時(shí)利用小波變換的多尺度特性將地震數(shù)據(jù)分解為不同頻帶數(shù)據(jù),實(shí)現(xiàn)多尺度反演。數(shù)值模擬實(shí)驗(yàn)結(jié)果表明,基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演,對(duì)初始模型和低頻數(shù)據(jù)的依賴(lài)程度降低,較常規(guī)全波形反演具有更好的穩(wěn)定性,受到“跳周”現(xiàn)象影響的可能性大大降低。
FWI; 最小平方濾波; 小波變換; 多尺度; 目標(biāo)函數(shù)
0 前言
全波形反演是一種利用疊前地震記錄的波形信息來(lái)重建地下介質(zhì)的物性參數(shù)的高精度建模方法。Gauthier等[1]和Mora[2]于上世界80年代實(shí)現(xiàn)了二維地震資料的全波形反演。實(shí)踐證明了全波形反演具有精細(xì)地刻畫(huà)地下地質(zhì)構(gòu)造的能力,但同時(shí)也存在著一些重要問(wèn)題(采集方式等對(duì)偏移距的限制;實(shí)際數(shù)據(jù)的頻率成分不能提供全波形反演所需的低頻信息;該方法對(duì)初始模型的依賴(lài)性較強(qiáng)等)。近年來(lái),全波形反演作為勘探地球物理領(lǐng)域的研究熱點(diǎn),發(fā)展迅速,針對(duì)傳統(tǒng)全波形反演存在的問(wèn)題提出了很多改進(jìn)方式和新的方法,方法理論和實(shí)際應(yīng)用方面都取得了很大的進(jìn)展,Shin等[3]提出了拉普拉斯傅立葉全波形反演,是解決反演所需低頻信息缺失問(wèn)題的重要突破;Warner[4]提出了自適應(yīng)全波形反演(AWI),使反演更為穩(wěn)定,有效地克服了“跳周”現(xiàn)象的影響;應(yīng)用上,Christian等[5]對(duì)西非地區(qū)海相碳酸鹽數(shù)據(jù)進(jìn)行了拉普拉斯傅立葉全波形反演,得到了較好的結(jié)果。
小波變換是一種有效的多尺度時(shí)頻分析方法。它對(duì)確定的信號(hào)有一種“集中”的能力[6-7],并且信號(hào)和噪聲在小波域具有不同的表現(xiàn)特征。由于這些時(shí)頻域局部特性和多分辨分析特點(diǎn),以及小波變換的低熵性、去相關(guān)性等,小波變換被廣泛地用于圖像處理和信號(hào)去噪方面[8-12]。考慮到單一方法的不足,一些學(xué)者提出將小波變換與各種濾波算法相結(jié)合的新算法[13-17];趙艷明等[13]提出了一種小波-維納濾波算法,證明了該組合算法比單一的小波閾值去噪或維納濾波去噪的效果更好;汪魯才等[14]提出了一種有效的基于小波變換與中值濾波相結(jié)合的干涉圖濾波算法;蔡國(guó)林等[16]提出了一種小波-維納濾波器,證明了利用小波變換的優(yōu)勢(shì)和維納濾波的統(tǒng)計(jì)特性進(jìn)行干涉圖濾波可以取得很好的效果。
為了解決全波形反演存在的問(wèn)題,將小波域最小平方濾波引入到全波形反演過(guò)程中,提出了時(shí)間域多尺度自適應(yīng)全波形反演。利用小波變換的多尺度特性對(duì)波場(chǎng)數(shù)據(jù)進(jìn)行分頻,從低頻帶數(shù)據(jù)開(kāi)始進(jìn)行反演。同時(shí)在每個(gè)頻帶中利用小波域最小平方濾波對(duì)模擬波場(chǎng)數(shù)據(jù)進(jìn)行濾波處理,達(dá)到調(diào)整模擬波場(chǎng)相位的目的。最終使得基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演對(duì)初始模型和低頻數(shù)據(jù)的依賴(lài)性降低,反演過(guò)程更為穩(wěn)定。
1 時(shí)間域全波形反演
二維全波形反演的目標(biāo)函數(shù)可以寫(xiě)為式(1)。
E=‖d-dobs‖2
(1)
其中:dobs為觀測(cè)到的地震數(shù)據(jù);d為正演模擬得到的地震數(shù)據(jù)。d可以表示參數(shù)m的函數(shù)即:
d=F(m)
(2)
其中:m為描述各種地球物理參數(shù)的矢量,如速度、密度、彈性參數(shù)等;F(·)表示依賴(lài)于m的地震波傳播過(guò)程。則目標(biāo)函數(shù)對(duì)m的一階導(dǎo)數(shù)為:
(3)
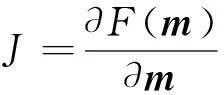
考慮時(shí)間域離散,式(1)目標(biāo)函數(shù)可改寫(xiě)為:
(4)
式中:Ns、Nr、Nt分別代表震源數(shù)目、檢波點(diǎn)數(shù)目、時(shí)間采樣點(diǎn)數(shù)。
伴隨狀態(tài)法求取的梯度可表示為:
(5)
其中:v表示速度;d為正傳波場(chǎng);R為拾取檢波點(diǎn)處波場(chǎng)的算子。
得到梯度后,我們可以選取適當(dāng)?shù)膬?yōu)化方法,確定合適的步長(zhǎng)a,利用式(6)迭代更新初始模型(Rn為模型更新量),即可得到全波形反演的結(jié)果。
mn+1=mn+a Rn
(6)
2 小波變換及小波域最小平方濾波
假設(shè)存在不同尺度的細(xì)節(jié)空間Wj和逼近空間Vj,
(7)
(8)
其中,任意子空間都是正交的,即Wj⊥Vj,由多分辨率分析可知:
V0= V1⊕W1=V2⊕W2⊕W1=
V3⊕W3⊕W2⊕W1=Λ
(9)
則對(duì)于一個(gè)信號(hào)f(t),可以把它分解為細(xì)節(jié)部分W1和逼近部分V1,然后再將逼近部分V1進(jìn)一步分解到下一個(gè)尺度空間,如此循環(huán),就可以得到任意尺度上的細(xì)節(jié)部分和逼近部分。將信號(hào)f(t)向不同的尺度空間Wj、Vj投影,可得到該信號(hào)在不同尺度上的細(xì)節(jié)信號(hào)和逼近信號(hào),即:
(10)
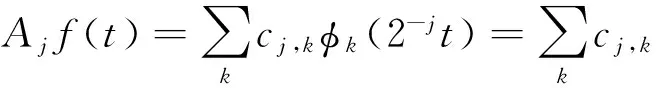
(11)
dj,k=[f(t),ψj,k(t)]
(12)
cj,k=[f(t),φj,k(t)]
(13)
其中:ψj,k(t)為小波函數(shù);φj,k(t)為尺度函數(shù);dj,k、cj,k分為細(xì)節(jié)系數(shù)和近似系數(shù)。若分解尺度為J,則有
(14)
式(14)即為離散小波變換的重構(gòu)公式,式(12)、式(13)就是小波變換的分解公式。
小波域中的最小平方濾波就是先對(duì)信號(hào)進(jìn)行小波變換,分解為近似系數(shù)和各個(gè)尺度上的細(xì)節(jié)系數(shù),然后對(duì)各尺度系數(shù)分別進(jìn)行濾波的過(guò)程。若將小波變換后的近似系數(shù)和細(xì)節(jié)系數(shù)cJ,k、dj,k作為濾波器的輸入信號(hào),對(duì)應(yīng)的濾波算子分別為u、fj,則實(shí)際輸出分別為:
AJ,k=cJ,k*u, Dj,k=dj,k*fj
(15)
若對(duì)應(yīng)的期望輸出信號(hào)分別為yJ,k、sj,k,則相應(yīng)的誤差能量為:
(16)
根據(jù)最小平方原理,當(dāng)誤差能量取最小值時(shí),即可得到最佳濾波算子u、fj。

圖1 濾波前后記錄對(duì)比圖Fig.1 Comparison of the record before and after filtering(a)濾波前;(b)濾波后
3 多尺度自適應(yīng)全波形反演
考慮對(duì)不同尺度地震信號(hào)地反演,對(duì)模擬波場(chǎng)和觀測(cè)波場(chǎng)分別進(jìn)行小波變換,抽取近似系數(shù)和不同尺度的細(xì)節(jié)系數(shù),即抽取不同頻帶的地震數(shù)據(jù)。對(duì)不同尺度的模擬波場(chǎng)數(shù)據(jù)進(jìn)行最小平方濾波來(lái)調(diào)整它的相位,對(duì)于J級(jí)多尺度小波變換,共需要進(jìn)行J+1次最小平方濾波:
AJ,k=cJ,ku,Dj,k=dj,kfj,j=1,2,…,J
(17)
其中:AJ,k為最小平方濾波后的近似系數(shù);Dj,k為濾波后的細(xì)節(jié)系數(shù);J代表分解尺度。
圖1為濾波前后記錄的對(duì)比圖,可以看到濾波后記錄間的相位差明顯減小。
則式(1)目標(biāo)函數(shù)可改寫(xiě)為如式(18)、式(19)所示。
(18)
(19)

(20)
其中:v表示速度;d為正傳波場(chǎng);R為拾取檢波點(diǎn)處波場(chǎng)的算子。得到梯度后,使用拋物線法確定最佳步長(zhǎng)(公式(21)),目標(biāo)函數(shù)φ在α0、α0+h、α0+2h三點(diǎn)處滿(mǎn)足φ0>φ1<φ2,確定步長(zhǎng)后依然按照公式(6)迭代更新初始模型。
(21)
4 數(shù)值模擬實(shí)驗(yàn)
4.1 Marmousi模型實(shí)驗(yàn)
從Marmousi模型中抽取大小為127×384個(gè)網(wǎng)格的模型,在模型表面增加11個(gè)網(wǎng)格的水層作為真實(shí)模型(圖2(a)),網(wǎng)格距為25 m,真實(shí)大小為3 450 m×9 600 m。為了使常規(guī)全波形反演方法易“跳周”,反演結(jié)果對(duì)比明顯,給出一個(gè)較差的初始模型(圖2 (b))。實(shí)驗(yàn)中使用混合震源方式,每個(gè)震源均為主頻相同的雷克子波,具有隨機(jī)設(shè)定的不同的激發(fā)時(shí)間,震源位置隨機(jī)分布于模型表面。
首先,用一個(gè)比較低的反演主頻,提供足夠的低頻信息進(jìn)行全波形反演。將震源主頻設(shè)置為6 Hz,采樣間隔為2 ms,接收時(shí)間為8 s。檢波器排列位于模型表面,各檢波點(diǎn)間距為25 m,共接收384道。采用有限差分算法正演,并應(yīng)用矩陣快速運(yùn)算,反演采用Fletcher-Reeves形式的共軛梯度法迭代更新,每次迭代至少需要兩次正演,反演過(guò)程中應(yīng)用2級(jí)小波變換。
反演結(jié)果如圖3、圖4所示。可以看到,在低頻信息充足的情況下,兩種算法都可以很好地重建速度模型,反演精確度較高,反演結(jié)果相差無(wú)幾。圖5所示為模型橫向6.5 km處,反演結(jié)果與真實(shí)模型及初始模型的縱向速度對(duì)比。從圖4(a)中可以看到,模型淺中部的反演速度與真實(shí)速度基本一致(<2 km),但對(duì)于深部,只能重建其構(gòu)造,而不能準(zhǔn)確地恢復(fù)速度信息。這是因?yàn)槟P椭械卣鸩ǖ哪芰糠植疾痪鶆颍瑴\部的能量比深部要強(qiáng),且全波形反演對(duì)振幅變化很敏感,加之實(shí)驗(yàn)中所用的初始模型較差,初始模型速度與真實(shí)速度值相差較大,尤其是深部高阻帶部分,這對(duì)恢復(fù)真實(shí)速度值也有很大的影響。
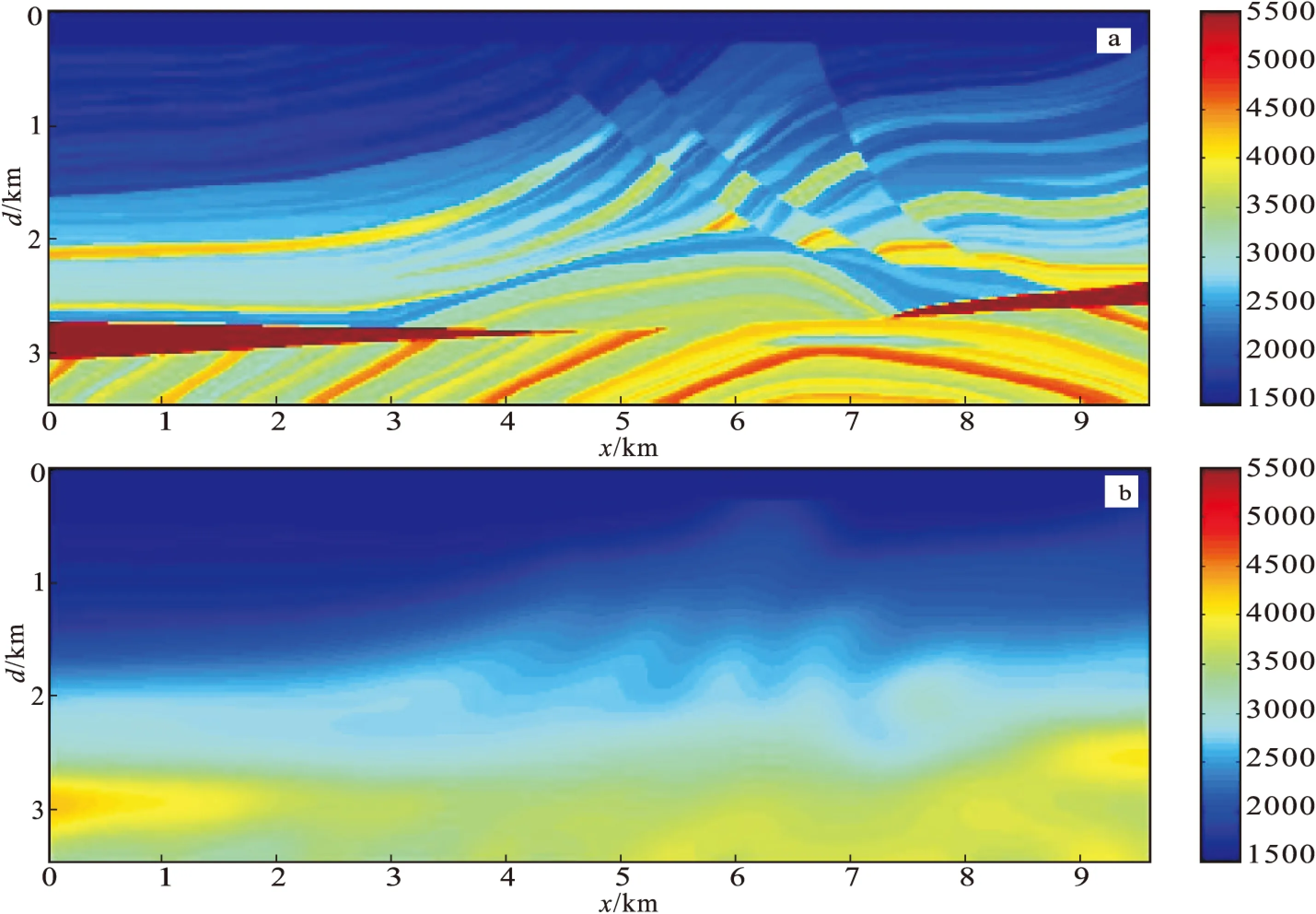
圖2 模擬實(shí)驗(yàn)所用速度模型Fig.2 Model used in numerical simulation experiment(a)真實(shí)模型;(b)初始模型
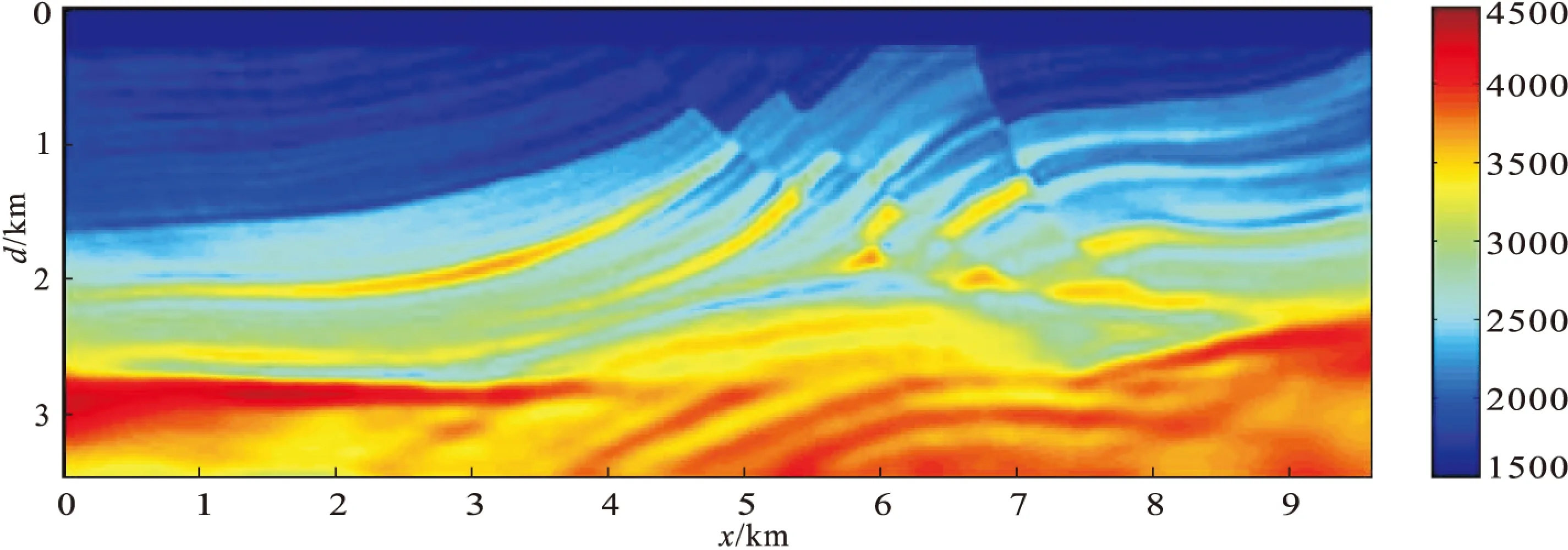
圖3 常規(guī)FWI反演結(jié)果Fig.3 Model recovered using conventional FWI
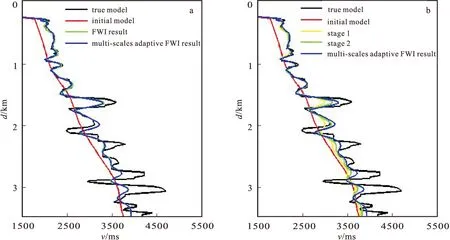
圖4 縱向速度對(duì)比Fig.4 Longitudinal velocity comparison of the result of multi-scales adaptive FWI based on wavelet transform(a)最終結(jié)果;(b)多尺度反演不同階段
圖5(a)~圖5(c)中,展示了多尺度自適應(yīng)反演的不同頻帶的結(jié)果。由圖5(a)可見(jiàn),低頻帶反演結(jié)果已經(jīng)大致得出模型的基本輪廓,而經(jīng)過(guò)中低頻反演和全頻帶反演之后,細(xì)節(jié)信息得到改善,界面和構(gòu)造越來(lái)越清晰。三個(gè)階段的反演中,低頻帶信息主要能夠恢復(fù)模型輪廓,而中低頻帶反演和全頻帶反演則對(duì)速度的正確更新有更重要的貢獻(xiàn)(圖4(b))。
4.2 缺少低頻情況下的對(duì)比實(shí)驗(yàn)
為了得到初始模型差且缺失低頻信息下的對(duì)比結(jié)果,將反演主頻提高到10 Hz,其他參數(shù)設(shè)置均保持不變。這樣提供反演的數(shù)據(jù)最低頻率大約為5 Hz左右,不能滿(mǎn)足常規(guī)全波形反演對(duì)低頻信息的需求。
常規(guī)全波形反演的結(jié)果如圖6所示,由于初始模型較差,造成模擬波場(chǎng)與觀測(cè)波場(chǎng)間的差異較大,加之此時(shí)低頻信息不足,導(dǎo)致常規(guī)l2范數(shù)陷入局部極小值,反演結(jié)果精確度較低,“跳周”現(xiàn)象嚴(yán)重。相比之下,可以看到圖7(c)所示的基于小波變換的多尺度自適應(yīng)全波形反演結(jié)果較好,并沒(méi)有出現(xiàn)嚴(yán)重的“跳周”現(xiàn)象,雖然相比6 Hz主頻時(shí)反演結(jié)果精確度有所降低,但依然能成功地反演出模型的主要構(gòu)造。實(shí)驗(yàn)過(guò)程中的反演結(jié)果同真實(shí)模型的誤差函數(shù)隨迭代次數(shù)的變換如圖8所示,常規(guī)FWI算法在大概200次迭代后,受“跳周”影響誤差函數(shù)很難再下降,而基于小波域最小平方濾波的全波形反演算法的誤差函數(shù)下降更多,反演結(jié)果模型精確度更高。
為了說(shuō)明不同反演頻帶的范圍,對(duì)小波變換后得到的不同頻帶的記錄進(jìn)行頻譜分析。抽取不同頻帶記錄的第181道(4.5 km處)數(shù)據(jù)分別進(jìn)行頻譜分析,結(jié)果如圖9所示。低頻帶范圍在5 Hz~7 Hz,中低頻帶范圍在5 Hz~9 Hz,而全頻帶范圍大致為5 Hz~13 Hz。
此外,全部測(cè)試都是在PC上完成的,其配置為Intel(R)Core(TM)i7-4790 CUP @3.60GHz和32 GB RAM。常規(guī)FWI算法迭代一次至少需要30 s,多尺度自使用全波形迭代一次至少需要50 s。雖然小波變換以及濾波過(guò)程增加了計(jì)算負(fù)擔(dān),效率有所降低,但考慮到算法的實(shí)用性,在反演穩(wěn)定性大幅增加的情況下,這些計(jì)算量是可以接受的。

圖6 多尺度自適應(yīng)全波形反演結(jié)果Fig.6 Model recovered by multi-scales adaptive FWI(a)低頻段;(b)低頻+中頻段;(c)全頻帶
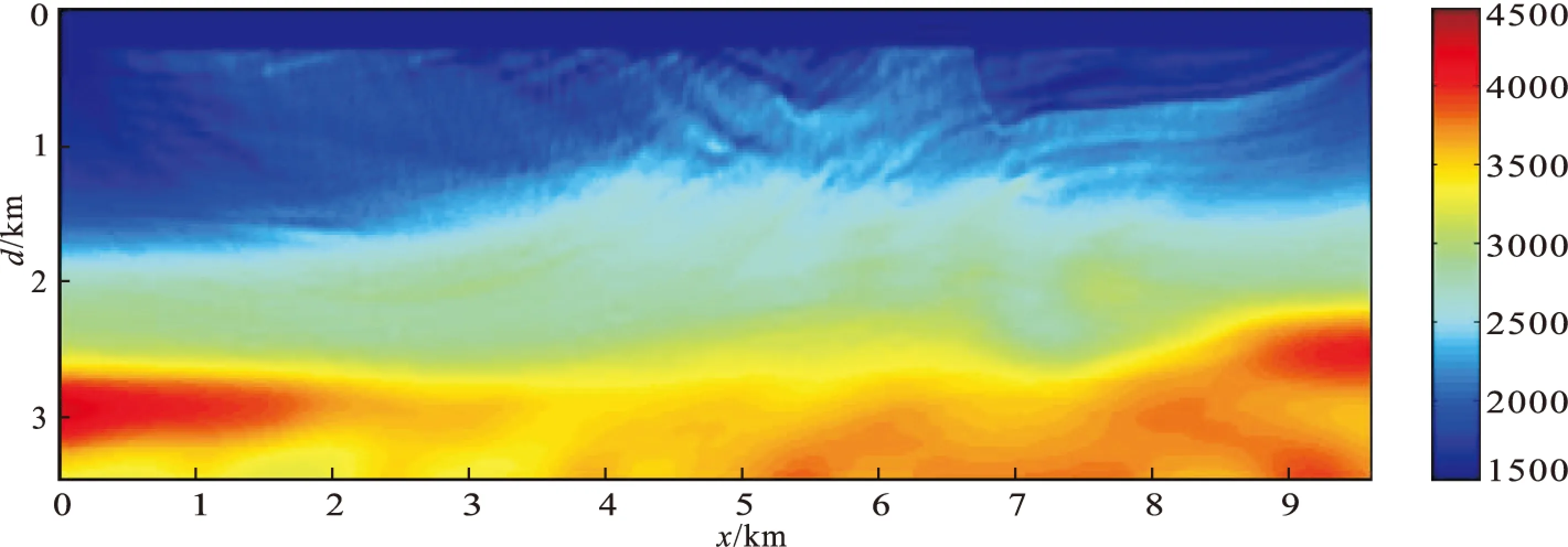
圖7 常規(guī)FWI反演結(jié)果Fig.7 Model recovered using conventional FWI

圖8 目標(biāo)函數(shù)曲線Fig.8 The error function curve(a)多尺度自適應(yīng)全波形反演;(b)常規(guī)FWI
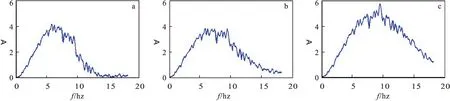
圖9 不同頻帶數(shù)據(jù)頻譜分析Fig.9 The spectrum of the trace extracted from data in different frequency bands(a)低頻;(b)中低頻;(c)全頻帶
5 結(jié)束語(yǔ)
對(duì)時(shí)間域FWI和小波變換以及小波域最小平方濾波的基礎(chǔ)理論進(jìn)行了研究,將小波域最小平方濾波應(yīng)用于時(shí)間域全波形反演中,充分利用小波變換的多尺度特性進(jìn)行數(shù)據(jù)分頻處理,實(shí)現(xiàn)了基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演,并得到了較好的實(shí)驗(yàn)結(jié)果。通過(guò)上述Marmousi模型數(shù)值模擬實(shí)驗(yàn)結(jié)果的對(duì)比,可以得出以下結(jié)論:
1)相比于常規(guī)全波形反演,基于小波變換的多尺度自適應(yīng)全波形反演對(duì)初始模型和低頻信息的依賴(lài)程度更低。當(dāng)初始模型較差時(shí),常規(guī)FWI受“跳周”現(xiàn)象影響嚴(yán)重,反演結(jié)果精確度較低,而多尺度自適應(yīng)全波形反演依然能夠很好地重建真實(shí)模型。
2)雖然增加的小波變換和濾波過(guò)程增加了計(jì)算量,對(duì)計(jì)算效率有所影響,但與常規(guī)FWI算法相比,基于小波變換的多尺度自適應(yīng)全波形反演的穩(wěn)定性更強(qiáng),考慮到處理實(shí)際數(shù)據(jù)存在的初始模型差、低頻缺失等問(wèn)題,這里算法具有更好的實(shí)用性,效率上也是可以接受的。
綜上所述,小波域最小平方濾波對(duì)調(diào)整模擬波場(chǎng)的相位信息具有很好的效果,基于小波域最小平方濾波的多尺度自適應(yīng)全波形反演從數(shù)據(jù)處理和多尺度策略?xún)煞矫嫣岣吡朔囱莘€(wěn)定性,有效地克服了“跳周”現(xiàn)象的影響,具有更好的實(shí)用性。
[1] GAUTHIER O, VIRIEUX J, TARANTOLA A.Two-dimensional nonlinear inversion of seismic waveform:mumeical results[J]. Geophysics, 1986, 51(7):1387-1403.
[2] MORA P. Nonlinear two-dimensional elastic inversion of multi-offset seismic data[J]. Geophysics, 1987,52(9):1211-1228.
[3] SHIN C,Y.HO CHA.Waveform inversion in the Laplace-Fourier domain[J].Geophysical Journal International,2009,177(3),1067-1079.
[4] WARNER,M.GUASCH,L.Adaptive waveform inversion - FWI without cycle skipping:Theory[R].EAGE Extended Abstracts,Amsterdam,2014.
[5] CHRISTIAN A.,RIVERA*,BERTRAND DUQUET.Laplace-fourier FWI as an alternative model building tool for depth imaging studies:Application to marine carbonates field[C].SEG,New Orleans,2015:1054-1058.
[6] I DAUBECHIES. The wavelet transform, time-frequency localization and signal analysis[J]. IEEE Trans. on IT.1990,36(5):960-1006.
[7] BURRUS C S, GOPINATH R A, GUO H T. Introduction to wavelets and wavelet transform[M]. Upper Saddle River, Prentic Hall, 1998.
[8] MALLAT S.Multi-frequency channel decompositions of images and wavelet models[J].IEEE Trans. Speech Signal Processing,1989,37:2091-2110.
[9] MALLAT S. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Trans on PAMI,1989,11(7):764-693.
[10]張旭東,詹毅,馬永琴.不同信號(hào)的小波變換去噪方法[J].石油地球物理勘探,2007,42(增刊):118-123.
ZHANG X D, ZHAN Y, MA Y Q. Approaches of denoise by wavelet transform of different signals[J]. Oil Geophysical Prospecting, 2007, 42(Supplement):118-123. (In Chinese)
[11]柳建新,韓世禮,馬捷.小波分析在地震資料去噪中的應(yīng)用[J].地球物理學(xué)進(jìn)展,2006,21(2):541-545.
LIU J X, HAN S L, MA J. Application of wavelet analysis in seismic data denoising[J]. Progress in Geophysics, 2006,21(2):541-545. (In Chinese)
[12]張華,潘冬明,張興巖.二維小波變換在去除面波干擾中的應(yīng)用[J].石油物探,2007,46(2):147-150.
ZHANG H, PAN D M, ZHANG X Y. Application of 2-D wavelet transformation in eliminating surface wave interference[J]. Geophysical Prospecting for Petroleum, 2007,46(2):147-150. (In Chinese)
[13]趙艷明,全子一.一種有效的小波- Wiener濾波去噪算法[J].北京郵電大學(xué)學(xué)報(bào), 2004,27(4):41-45.
ZHAO Y M, QUAN Z Y. An efficient wavelet-wiener denoising Algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2004,27(4):41-45. (In Chinese)
[14]汪魯才,王耀南,毛六平.基于小波變換和中值濾波的InSAR干涉圖像濾波方法[J].測(cè)繪學(xué)報(bào),2005,34(2):108-112.
WANG L C, WANG Y N, MAO L P, et al. An algorithm of interferometric phase filter of InSAR based on wavelet analysis and median filter algorithm[J]. Acta Geodaetica et Cartographica Sinica,2005,34(2):108-112. (In Chinese)
[15]田沛,李慶周,馬平,等.一種基于小波變換的圖像去噪新方法[J].中國(guó)圖形圖像學(xué)報(bào), 2008, 13(3): 394-399.
TIAN P,LI Y Z,MA P,et al.A new method based on wavelet transform for image denoising[J].Journal of Image and Graphics,2008,13(3):394-399.(In Chinese)
[16]蔡國(guó)林,李永樹(shù),劉國(guó)祥.小波-維納組合濾波算法及其在InSAR干涉圖去噪中的應(yīng)用[J]. 遙感學(xué)報(bào),2009,13(1):129-136.
CAI G L, LI S G, LIU G X. Wavelet-wiener combined filter and its application on InSAR interferogram[J]. Journal of Remote Sensing,2009, 13(1):129-136. (In Chinese)
[17]張涇周,張光磊,戴冠中.自適應(yīng)算法與小波變換在心電信號(hào)濾波中的應(yīng)用[J].生物醫(yī)學(xué)工程學(xué)雜志,2006, 23(5): 977-980.
ZHANG J Z, ZHANG G L, DAI G Z. The application of adaptive algorithm and wavelet transform in the filtering of ECG signal[J]. Journal of Biomedical Engineering, 2006,23(5): 977-980. (In Chinese)
[18]PLESSIX R E.A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006,167(2):495-503.
Multi-scales adaptive full waveform inversion based on the wavelet domain least square filter
BAI Lu, HAN Li-guo, ZHANG Pan, HU Yong
(Jilin University, Changchun 130011, China)
Conventional full waveform inversion (FWI) has a strong dependence on the initial model and low frequency data, it is often suffers from cycle skipping when this two conditions are not met. In order to solve the problem, we introduced the wavelet domain least square filter to FWI, and took advantage of the multiscale characteristic of the wavelet transform. It can effectively avoid the influence of cycle skipping in the inversion procedure, and improves the stability of FWI. Wavelet domain least square filter has the higher accuracy than the time domain, with this can narrow the phase difference between the predicted data and observed data, and construct a new objective function, to make the inversion procedure steadily converge to the global minimum. Meanwhile, with the multi-scales characteristic of wavelet transform, the data can be divided into different frequency bands, and implement the multi-scales inversion. The result of numerical simulation experiment demonstrates that multi-scales adaptive FWI based on the wavelet transform is much less dependent on initial model and low-frequency data. The method can be immune to cycle skipping, and more robust than conventional FWI.
FWI; least square filter; wavelet transform; multi-scales; objective function
2016-03-23 改回日期:2016-04-19
國(guó)家“863”計(jì)劃重大項(xiàng)目課題(2014AA06A605)
白璐(1991-),女,碩士,研究方向?yàn)榈卣鸩▓?chǎng)模擬與波形反演,E-mail:1124739332@qq.com。
1001-1749(2016)05-0618-08
P 631.4
A
10.3969/j.issn.1001-1749.2016.05.07

