埃博拉病毒傳播模型及規律預測

褚雨薇 管祥善 劉琦 王煜凱

摘要：埃博拉病毒是一種能引起人類和靈長類動物產生埃博拉出血熱的烈性傳染病病毒。文章以2014年西非疫區為參照，建立虛擬環境的常微分方程組，利用四階龍格—庫塔法求解其數值解，具體通過C語言程序設計實現，并據此研究埃博拉病毒的傳播規律，分析隔離措施的嚴格執行和藥物治療效果的提高等措施對控制疫情的作用。

關鍵詞：數學建模;埃博拉病毒;常微分方程組數值解;四階龍格—庫塔法;西非疫區 文獻標識碼：A

中圖分類號：O175 文章編號：1009-2374（2016）04-0194-03 DOI：10.13535/j.cnki.11-4406/n.2016.04.096

1 模擬真實環境

埃博拉病毒的自然宿主雖尚未最后確定，但已有多方證據表明猴子及猩猩等野生非人靈長類動物有埃博拉感染現象。該病毒的傳播途徑分為人畜傳播、人人傳播兩種。2014年，在幾內亞、塞拉利昂和利比里亞等國，許多受埃博拉病毒影響的人口都以叢林肉為重要的蛋白質和營養物質來源，與叢林中動物接觸頻繁。這為人畜之間的病毒傳播創造了條件。

我們現假設兩個感染埃博拉病毒的虛擬種群：即某地區內的20萬居民和3000只猩猩。人能以一定的概率接觸到所有的猩猩，當接觸到有傳播能力的猩猩后有一定概率感染病毒，而人發病之后與猩猩的接觸可以忽略。人與猩猩的潛伏期都為2周。并在出現疫情41周后模擬外界醫療力量的介入，使得人類與猩猩不再發生接觸，且隔離治療人群的治愈率提高到80%。模擬數據詳見附錄。

2 建立數學模型

2.1 模型假設

（1）依據人或猩猩的健康狀態，將人或猩猩劃分為健康者、埃博拉感染者（也稱患病者）、退出者（含自愈者、死亡者）;（2）自然封閉條件下，猩猩無自然遷移，故無病源的流入、流出，種群數量不變。人類數量龐大，在無大規模遷移的情況下，認為人類數目為一定值，保持不變;（3）健康者中不包含退出者;（4）人和猩猩自愈后二度感染的概率均為0，人被治愈后二度感染的幾率為0;（5）不存在有效免疫藥物可使人對埃博拉病毒產生免疫，同時猩猩對病毒也不免疫;（6）人的傳染途徑有人傳染人、猩猩傳染人兩條。兩條途徑的傳染率并不相同，分別假設為傳染率C1和傳染率C2。C1猩猩與猩猩之間傳染途徑只有猩猩傳染猩猩一條，假設猩猩之間的傳染率為C0;（7）患病人無法傳染患病猩猩;（8）41周外界介入后，猩猩與人的傳播途徑切斷，隔離患者的治愈率提高到80%，同時未被隔離的患者治愈率不變。

2.2 符號說明

符號說明如表1所示：

3 模型的建立與求解

3.1 數據處理

根據累計死亡個體數，求得每周死亡個體數。同理，根據累計自愈個體數，求得每周自愈個體數。由每周仍處于發病狀態的個體數加本周自愈個體數和本周死亡個體數得到每周總患病個體數。

由每周總患病個體數比總體數目得到每周患病個體在總體中的比例A（t）;由相鄰兩周每周患病數相減得到每周新增患病數。由總體個數減去新增病例累計和獲得健康個體數，并由此得到健康個體在總體中的比例J（t）;由累加自愈治愈人數與累加死亡人數得到退出者總數量，并由此得到退出者在總體中的比例T（t）。

由于埃博拉病毒的潛伏期是兩周，所以任意一周的新增病例是兩周前處于患病狀態的個體傳染的。由新增病例數比兩周前處于患病狀態的個體數得到該周埃博拉病毒傳染率，由此計算出每一周的傳染率。通過MATLAB繪圖，我們得到其近似曲線為一條平行于X軸的曲線，所以通過加權平均求得平均傳染率。

因為人類最初患病個體不可能為人類傳染所致，所以兩周內出現的患病者必為由猩猩傳播而來的。最初兩周，人每周新增的患病個數除以處于兩周前患病狀態的猩猩個數得到猩猩與人之間平均傳染率C1。

兩周之后人患病可由猩猩和人傳播兩種途徑導致，猩猩每周處于患病狀態的數量和C1已知，所以每周由猩猩傳播導致人患病的數量可求出，用每周新增患病人數減去每周猩猩傳播導致人患病的數量，即每周由人傳染導致的患病數量。由每周人傳染導致的患病數量除以兩周前未被隔離處于患病狀態的人數可得到每周埃博拉人與人之間傳染率C1，通過MATLAB畫出C2的圖像，可以發現其圖像為平行于x軸的曲線，可通過加權平均求出人與人之間平均傳染率C2。

死亡率是由本周死亡個數比本周總病例數得到。我們由此求得每一周的死亡率。通過MATLAB繪圖我們得到一條同樣近似平行于X軸的曲線，所以通過加權平均，求得疫情穩定后平均死亡率。

每周處于未隔離的患者人數處于每周的處于患病狀態的總人數可得到每周的未隔離率G，其圖像為平行于x軸的曲線，通過加權平均求出平均未隔離率G。

同理，我們還得到疫情穩定后的平均自愈及治愈率。我們近似地認為，在病情爆發后不久，即疫情穩定后，周感染率、周死亡率、周治愈自愈率、周未隔離率都是常值。

3.2 埃博拉病毒的傳播模型

由假設知，猩猩患病只能由猩猩傳播。每個患病猩猩每周可使得只的健康猩猩變為患病猩猩，由患病猩猩數量得每周共有只健康猩猩被感染。即患病猩猩的增加率，又因為每周自愈的猩猩數目為，死亡的猩猩數目為，所以猩猩患病數隨時間變化滿足：

同理，我們得到人類的傳播模型（由前述，所有腳標為2的符號均為人類相關數據，腳標為1的符號為與猩猩相關數據）：

3.3 模型求解

通過聯立方程組和數據處理，我們使用四階龍格—庫塔法分別求出人和猩猩群體中健康者和患病者的比例的數值解。

通過C程序設計編譯程序求解模型所用常微分方程組的數值解。該程序在前四十組解得檢驗中擬合程度極高，故由此得到較為可靠的預測數據。C語言程序代碼詳見附錄。

數據擬合如下：

3.4 建立使用免疫藥物后的模型

未被隔離患者的治愈率和被隔離患者的治愈率加權平均后得到患者的平均治愈率Zh。1-Zh為死亡率與未被治愈率之和。默認死亡率與未被治愈率權重不變。在（1-Zh）中，可以算出死亡率的權重和未被治愈率的權重。在嚴格控制人類與黑猩猩接觸并使用特效藥后的數學模型如下：

將之與隔離前模型對照后發現，特效防疫藥物的使用極大地提高了治愈率Zh，快速地降低了患病數。而隔離黑猩猩的措施將黑猩猩傳染致病人數降為0。

綜上，兩種措施都有效地預防了疾病的進一步擴散，抑制了疾病的傳播，使患病人數的增長率由正變負，從而導致患病數在短期內大量且持續減少。

4 模型的評價與推廣

4.1 模型優勢

（1）種群數量較小時，通過求解比例的變化得出結果較為精確;（2）可以動態地描述種群發病率、死亡率、自愈率、治愈率、傳染率等多種特征量;（3）四階龍格—庫塔法通過數值求解常微分方程組，很好地擬合了給定的原始數據。

4.2 模型缺陷

（1）由于通過比例而非數量求解，所以當種群數量較大且比例變化不明顯時誤差較大;（2）認為兩個“虛擬種群”內部個體總數在隨時間變化時基本不變，未考慮個體總數的時間變化率。

5 附錄

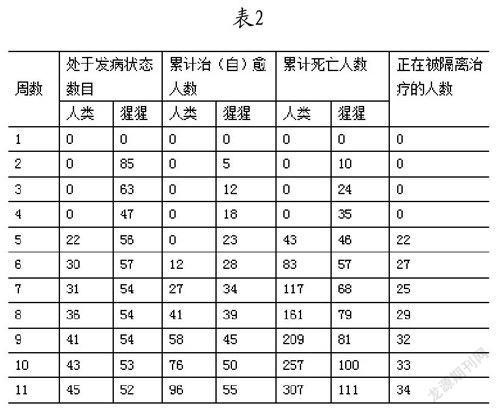
5.1 模擬數據

模擬數據如表2所示：

5.2 C語言程序代碼

參考文獻

[1] 李信真.計算方法[M].西安：西北工業大學出版社，2013.

[2] H.Nishiura，G.Chowell.EARLY TRANSMISSION DYNAMICS OF EBOLA VIRUS DISEASE（EVD）[J].WEST AFRICA，2014，（8）.

[3] 甄西豐.實用數值計算方法[M].北京：清華大學出版社，2006.

[4] 劉來福，何青.用Maple和MATLAB解決科學計算問題[M].北京：高等教育出版社，1999.

（責任編輯：王 波）