幾何畫板在中學數學教學中的實踐及體會
徐娟


隨著科學技術的不斷發展,計算機在中學數學教學中的應用不斷受到重視和強化.通過計算機技術的使用,使得數學知識變得更加直觀、形象,將復雜枯燥的數轉變成生動形象的形.幾何畫板作為整合數學知識與信息技術的主要工具,具有靈活繪圖、智能變換、動態演示等優勢,為中學數學教學注入新鮮血液.由于幾何畫板制作簡單、操作方便,已經逐漸成為廣大中學教師的信息化教學首選.在本文中,我們將從中學數學教學實踐的角度出發,探討幾何畫板在教學中的應用.
一、靈活繪圖,性質探析
概念是數學的基礎,性質則是對概念的升華和應用.在中學數學中,函數、不等式、方程、幾何圖形等,涉及眾多的數學概念,對應眾多的數學性質.幾何畫板作為聯系數與形的電子化橋梁,具有靈活繪圖的特點,對數學概念的性質揭示起到重要作用.
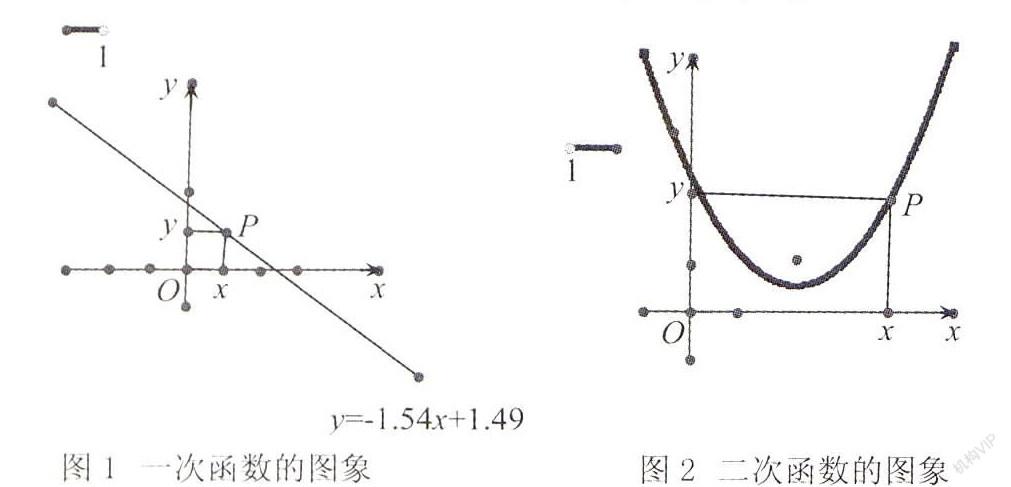
例如,在函數性質的教學中,我們往往是要求學生自行繪制坐標系,然后將給定的函數利用描點法進行圖形繪制.然后通過對不同系數條件下函數圖形的變化分析,得到對應的函數性質.但在幾何畫板的幫助下,這些程序我們都可以利用計算機進行,直接要求學生進行幾何畫板繪圖,迅速揭示函數性質.對于一次函數的教學,學生們在坐標系內任意繪制一條直線,便可以迅速得到它的一元一次函數表達式.然后,要求學生嘗試拖動、旋轉直線,觀察其系數值k、b的變化規律.如下圖所示,我們拖動點P,發現其橫縱坐標與系數的變化規律.于是,我們便可以直觀地得到函數單調性.對于系數b,我們同樣可以要求學生進行自主探究,利用幾何畫板尋找其性質規律.
對于二次函數,我們同樣可以采取幾何畫板的性質探究模式.首先,通過幾何畫板可以迅速得到二次函數解析式及其圖象.然后,通過拖動圖形中的P點,可以發現二次函數的變化規律,找出其對稱軸、單調區間等.通過轉動圖形,可以發現函數開口與解析式系數的關系.對于其余系數的變化規律探究,我們引導學生繪制對照性圖形,迅速發現規律.對此,我們必須在備課時設置好幾何畫板的教學內容,從而有效掌控課堂教學節奏.
二、動態演示,訓練思維
數與形是數學學科的兩大基本內容,數形結合的思想貫穿于整個中學教學.幾何畫板能夠有效地聯系數與形,是一種重要的數學思想,對學生思維訓練有著重要作用.對此,我們不妨利用數形結合與智能變換的方式,幫助學生掌握該思想,有效地構建數學模型.
例題 有一張三角形紙片ABC,其中BC=6,∠C=90°,∠A=30°.
(1)如圖3,若用這張紙片裁剪出一個矩形CDEF,使點D、E、F分別落在AC、AB、BC上,且使矩形CDEF的面積最大,則點E應選在何處?
(2)如圖4,若用這張紙片裁剪出一個矩形DEFG,使點D、G分別落在AC、BC上,點E、F均在AB上,且使矩形DEFG的面積最大,則點E應選在何處?
三、智能變化,自主探究
在新課改背景下,數學教師對學生的自學能力要求不斷提高,要求學生能夠利用幾何畫板實現對數學知識的自主探究.幾何畫板的智能變換功能為學生的自主探究提供了可行性工具,同時也鍛煉了學生的探究能力和實踐操作能力,提高了數學課堂的教學效率.
例如,在三角形中線定理的教學中,我為學生們提出了以下的自主探究課題,要求學生們利用幾何畫板的智能變換功能,對三角形中線交點位置進行探究.首先,學生們任意繪制了一個三角形,再利用幾何畫板繪制出它的三條中線,發現所有的中線都交于三角形內部一點.然后,學生們提出質疑:是否所有三角形的中線都交于圖形內部一點呢?于是,他們通過拖動定點A,得到不同類型三角形的中線交點位置.顯然,在銳角、直角、鈍角三角形中,它們的中線都紛紛交于圖形內部一點.此時,學生們便可以初步得到三角形中線都交于一點的性質.此時,學生們也實現了對三角形中線性質的自主探究.
總之,幾何畫板在中學數學教學中有著非常廣泛和有效的運用,是數學知識與信息技術相結合的完美體現.雖說幾何畫板在中學數學教學中已經取得一定的效果,但其中還存在很多的不足之處,作為一線數學教師,我們還必須繼續實踐探索,為學生們總結出更加科學有效的幾何畫板教學模式.

