水工隧道動力深、淺埋劃分限界研究及試驗驗證

張 碧，呂曉春

(1.陜西鐵路工程職業技術學院，陜西渭南714000；2.華北水利水電大學資源與環境學院，河南鄭州450011)

?

水工隧道動力深、淺埋劃分限界研究及試驗驗證

張 碧1，呂曉春2

(1.陜西鐵路工程職業技術學院，陜西渭南714000；2.華北水利水電大學資源與環境學院，河南鄭州450011)

隧道動力深、淺埋劃分限界屬于隧道結構的固有特性，受圍巖類別、隧道結構形狀、隧道跨度等因素的影響，不受外界因素(如地震波種類等)的影響。計算分析和振動臺模型試驗驗證表明，隧道動力深、淺埋劃分限界值受圍巖類別的影響較大；矩形隧道對其敏感性較大，圓形隧道的敏感性較小；隧道跨度對其有一定的影響。

隧道；動力劃分限界；振動臺試驗；地震波

0 引 言

截至目前，全球發生過許多次重大地震。在這些地震中，隧道結構都發生了不同程度的破壞。震害統計發現，隧道埋深大于50 m 時破壞程度明顯減小，在300 m以下沒有嚴重的破壞，受破壞的地下洞室有35%的埋深小于50 m[1]。在地震作用下，隧道埋深對隧道的受力和變形有很大影響，對深、淺埋隧道需要采用不同的計算方法。目前，公路隧道抗震設計中或者沒有區分深、淺埋，或者仍然采用靜力分析中深、淺埋劃分方法[2]，不能反應出地震波作用的動力實質。因此，進行隧道動力深、淺埋劃分限界研究是必要的。

隧道埋深是影響地震動力響應的一個重要因素。舒亞俐等[3]對不同埋深構筑物的動力響應進行研究認為，構筑物的振動頻率隨埋深的增加而增大，總體位移隨埋深的增加而減少，地震慣性力隨埋深增加而減小；鄭永來等[4]對國內外城市地下結構的震害情況進行統計分析后認為，地下管道的破壞隨埋深的增加而減小，地下結構埋深越大，由地震面波導致的能量越小，震害應減輕；于翔[5- 6]分析了1995年阪神地震中地下結構的破壞情況發現，上層破壞比下層破壞嚴重，地下結構上部土層越厚，破壞越輕；李海波等[7]研究了地震荷載作用下地下巖體洞室位移特征的影響因素認為，地下洞室位移響應隨埋深的增加而減小，洞室位移響應存在臨界埋深；李加林等[8]運用FLAC就珠三角軟土地層隧道埋深對地鐵運行誘發的相關振動影響規律進行分析表明，埋深越淺則動力響應越強，埋深越大則動力響應越弱；鄭穎人等[9]通過模型試驗與數值分析方法研究了靜力條件下隧道從淺埋到深埋的破壞過程，根據壓力拱(普氏壓力拱) 確定深、淺埋的分界線。

以上研究表明，隧道埋深對隧道地震響應有很大的影響，但依靠靜力條件下的劃分標準確定地震作用下隧道的動力深、淺埋是不準確的，有關隧道動力深、淺埋劃分方面的研究還未見相關報道。為此，本文通過數值計算和振動臺模型試驗，劃分隧道動力深、淺埋。

1 數值計算原理與方法

計算中將隧道作為平面應變問題處理，隧道襯砌和圍巖均采用塊體(Plane42 單元，二維實體結構模型用作平面應變單元)，圍巖的破壞準則采用D-P準則，計算模型的尺寸高h×寬b=300 m×500 m，模型左、右兩側使用粘彈性邊界，使用彈簧單元combin14模擬。計算模型見圖1。具體的彈性和阻尼參數計算如下

(1)

CBT=ρcS

CBN=ρcP

式中，KBT、KBN分別為切向和法向彈簧的彈性系數；CBT、CBN分別為切向和法向的阻尼系數；ρ為圍巖的密度；R為邊界點到隧道中心的距離；cS、cP分別為地震橫波波和縱波波速；kT、kN為調整系數，在0.5～1.2的范圍內取值，通過數值試算確定[10]。

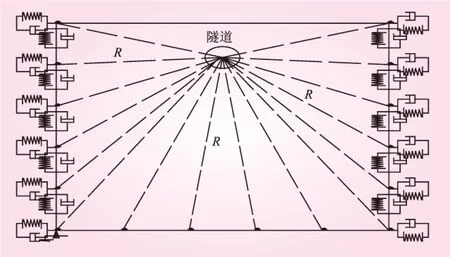
圖1 計算模型

為了對比分析，隧道采用矩形、馬蹄形和圓形隧道結構。動力阻尼C采用瑞利阻尼，即

C=αM+βK

(2)

式中，M為系統質量矩陣；K為剛度矩陣；α為與質量成比例的阻尼系數；β為與剛度成比例的阻尼系數。

對于多自由度系統，任意系統角頻率ωi的臨界阻尼比ξi是角頻率為ωi的第i階模態臨界阻尼的一部分，可以從下式得到

(3)

模擬計算隧道結構在El_Centro地震波(前8.0s)和2008年汶川地震波作用下的地震響應，兩者的頻率和峰值分布不同，對比分析可以反應出隧道結構的波動特性。加速度峰值均取0.3g。相關輸入地震波時程見圖2。

圖2 輸入地震波時程

2 數值計算結果分析

2.1 不同圍巖類別

本節計算時，選取隧道結構為馬蹄形，輸入El_Centro地震波，提取了襯砌外側拱頂處的剪切應力τxy。不同圍巖類別襯砌應力隨隧道埋深變化見圖3。圖中，B為隧道跨度。

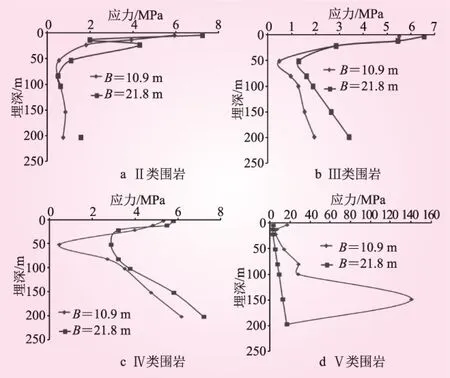
圖3 不同圍巖類別襯砌應力隨隧道埋深變化

從圖3可知，在地震波作用下，隧道襯砌的剪應力在隨埋深變化中存在拐點，拐點處的隧道埋深可作為隧道動力深、淺埋限界；隧道動力深、淺埋限界受圍巖類別影響較大；隧道跨度對隧道動力深、淺埋限界有一定的影響(圖3d中，埋深150 m處數值有突變，應是計算誤差所致，可忽略)。

2.2 不同隧道結構形狀和跨度對比

為了分析影響隧道動力深、淺埋限界的影響因素，本節考慮了隧道結構形狀和隧道跨度2種因素進行了對比分析。不同隧道結構形狀襯砌應力隨隧道埋深變化見圖4。

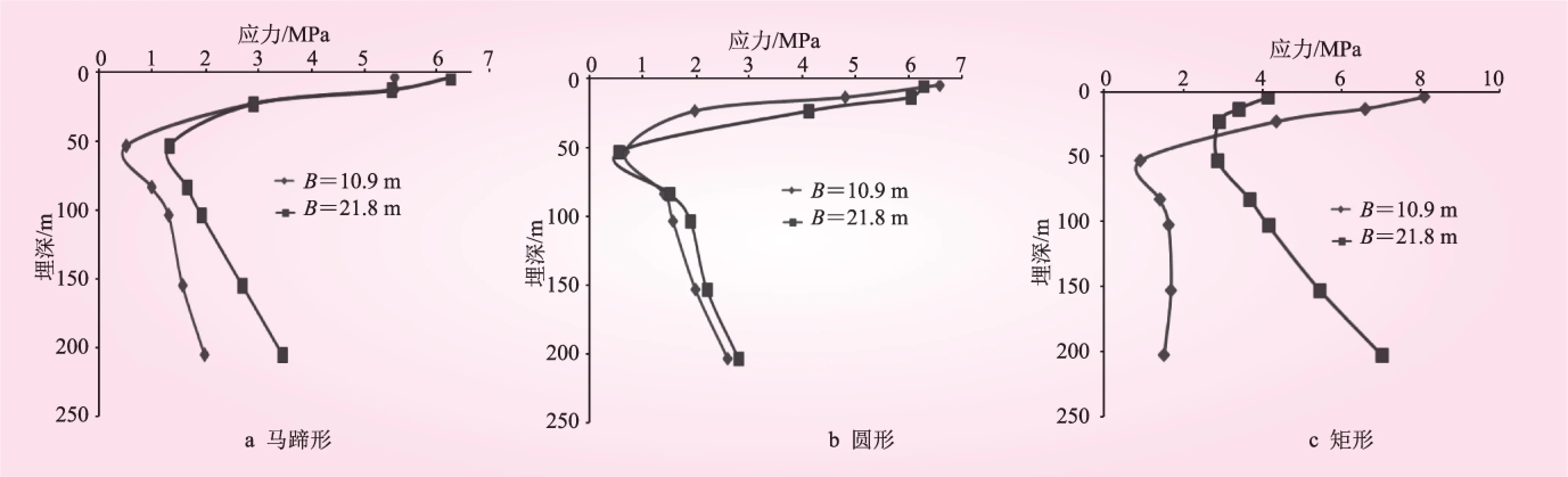
圖4 襯砌應力隨隧道埋深變化

由圖4可知，隧道結構形狀對隧道動力深、淺埋限界的影響不大；在不同的隧道結構形狀條件下，隧道跨度對隧道襯砌動應力和隧道動力深、淺埋限界的敏感性不同。其中，圓形隧道的敏感性較小，矩形隧道的敏感性最大；隧道跨度對隧道動力深、淺埋限界有一定的影響，但對不同結構形狀隧道的影響不同，對矩形隧道影響最大，對圓形隧道影響最小。

2.3 不同地震波對比

由上述分析可知，矩形隧道襯砌動應力對隧道動力深、淺埋限界的敏感性最強。本節計算分析了矩形隧道在El_Centro波和汶川波2種不同地震波(同為0.3g)作用下隧道動力深、淺埋限界的變化(見圖5)。

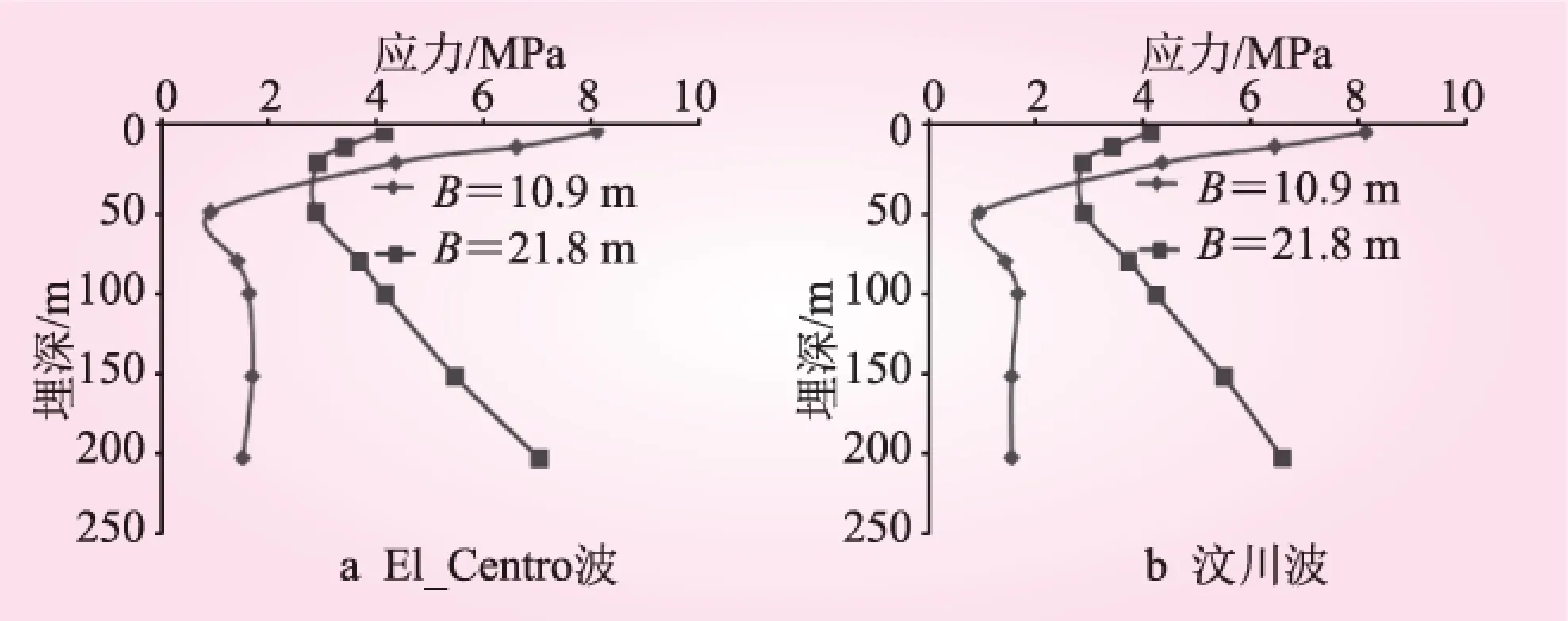
圖5 不同地震波作用下襯砌應力隨隧道埋深變化

從圖5可知，地震波種類的不同對隧道動力深、淺埋限界的影響不明顯；隧道動力深、淺埋限界應該是隧道自身的特性，與所受的地震波種類關系不大。

3 振動臺模型試驗設計

本試驗是為了驗證地震作用下隧道結構的響應規律，屬于動力試驗，應該用到動力相似準則。動力學運動方程可用矩陣方程表示如下

[M][a]+[C][v]+[K][u]=[F]

(4)

式中，[M]為質量矩陣；[a]為加速度矩陣；[C]為阻尼矩陣；[v]為速度矩陣；[K]為剛度矩陣；[u]為位移矩陣；[F]為荷載矩陣。

本試驗為對比驗證性試驗，綜合考慮振動臺承載能力、臺面尺寸、具體隧道尺寸和制作工藝等多種因素，對隧道原型進行適當簡化，試驗用長50 cm、寬50 cm、高80 cm的模型箱作為隧道洞口段模型，幾何相似比為1∶40；隧道襯砌采用了圓形襯砌，外徑15 cm，襯砌厚度1 cm。試驗模型見圖6。圖中虛線所示的襯砌為在不同深度處埋設襯砌，以模擬不同隧道埋深情況。

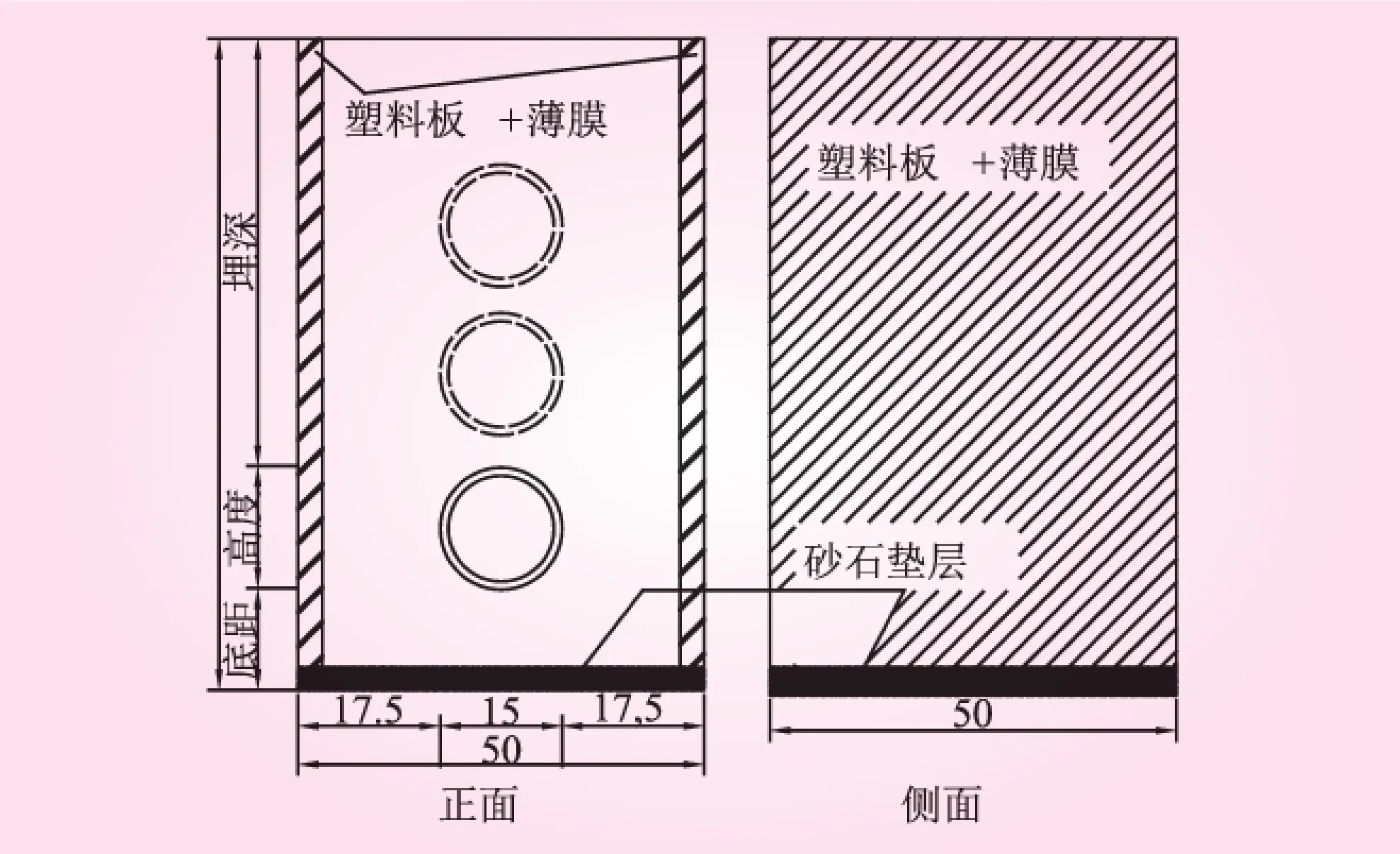
圖6 振動臺試驗模型(單位：cm)

振動臺提供水平方向的地震波輸入，輸入的地震波為El_Centro地震波(前8.0 s)和2008年汶川地震波，地震波的加速度峰值均取0.1g、0.2g、0.3g和0.4g。

用高強石膏模擬襯砌，用粉煤灰、石英砂、石膏、鋸末和機油的混合物模擬圍巖。石膏和機油主要等效圍巖的粘聚力c值[11]，粉煤灰和石英砂作為主要的骨料，通過調節其密度使顆粒級配滿足試驗要求。在確定襯砌材料時，根據水膏比為0.8∶1、0.9∶1、1∶1、1.1∶1和1.2∶1等5種情況分別做成標準圓柱體試件，然后放在萬能試驗機上進行分級加載壓縮試驗，確定其彈性模量在0.5～2.9 GPa。實際隧道一般采用C25混凝土作為二襯材料，其彈性模量為17.5～30 GPa。確定襯砌材料的彈性模量相似比為1∶20，據此選用水膏比為1.05∶1。將粉煤灰、石英砂、石膏、鋸末和機油等材料按照不同的配合比進行混合[12]，參照實際圍巖材料的物理性質指標，進行正交試驗來確定試驗材料的相似比。

將隧道襯砌外側上(Y1)、下(Y2)、左(Y3)和右(Y4)4個部位(見圖7)的剪切應力測試結果統計繪圖(見圖8)。振動臺試驗結果與前述的數值計算結果對比分析可知，隧道振動臺模型試驗進一步驗證了隧道動力深、淺埋限界的存在；振動臺模型試驗的結果與數值計算結果基本一致(限界值均在45～50 m)；隧道襯砌不同部位(上、下、左、右)處的動力深、淺埋限界值基本一致。

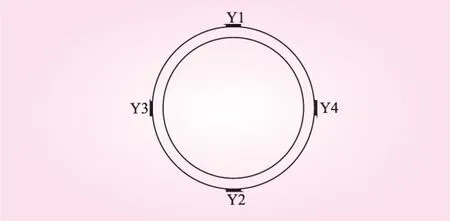
圖7 測試點布置

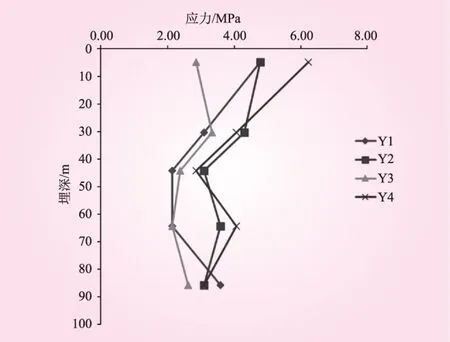
圖8 振動臺試驗結果

4 結 語

通過計算分析和振動臺模型試驗，證明了隧道動力深、淺埋限界的存在，并分析了其影響因素。得到如下結論：

(1)計算分析發現隧道動力深、淺埋限界是確實存在的，且與隧道的靜力深、淺埋限界值有所區別。

(2)隧道動力深、淺埋限界與圍巖類別、隧道結構形狀、隧道跨度等因素有關，屬于隧道結構的內在特性，與所受地震波的種類無關。

(3)隧道動力深、淺埋限界值受圍巖類別的影響較大；隧道結構形狀影響因素中，圓形隧道的敏感性較小，矩形隧道的敏感性最大；隧道跨度對動力深、淺埋限界值有一定的影響。

(4)隧道振動臺模型試驗驗證了隧道動力深、淺埋限界的存在，并且得到了與數值計算一致的結論。

[1]SHARMA S， JUDD W R. 地震對地下洞室的破壞[J]. 雷謙榮， 譯. 地下空間， 1992， 12(4)： 335- 344．

[2]JTG/T D70—2010 公路隧道設計細則[S].

[3]舒亞俐. 構筑物不同埋深時地震動反分析探討[J]. 特種結構， 1997， 14(4)： 49- 55.

[4]鄭永來， 楊林德. 地下結構震害與抗震對策[J]. 巖石力學與工程學報. 2001， 20(1)： 70- 73．

[5]于翔. 地鐵建設中應充分考慮抗地震作用—阪神地震破壞的啟示[J]. 鐵道建筑技術， 2000(6)： 32- 35．

[6]于翔. 地下建筑結構應充分考慮抗震問題—1995年阪神地震破壞的啟示[J]. 工程抗震， 2002(4)： 17- 20.

[7]李海波， 馬行東， 李俊如， 等. 地震荷載作用下地下巖體洞室位移特征的影響因素分析[J]. 巖土工程學報， 2006， 28(3)： 358- 362.

[8]李加林， 鄧飛皇. 隧道埋深對地鐵運行誘發振動的影響分析[J]. 科學技術與工程， 2007， 7(15)： 3819- 3822．[9]鄭穎人， 徐浩， 王成， 等. 隧洞破壞機理及深、淺埋分界標準[J]. 浙江大學學報： 工學版， 2010， 44(10)： 1851- 1856．

[10]杜修力， 趙密， 王進廷. 近場波動模擬的人工應力邊界條件[J]. 力學學報， 2006， 38(1)： 49- 56．

[11]王明年， 林國進， 于麗， 等. 隧道抗震與減震[M]. 北京： 科學出版社， 2012.

[12]蔣樹屏， 蔣華， 王曉雯， 等. 高烈度地震區公路隧道洞口段大型振動臺模型試驗方案設計[J]. 公路， 2009(10)： 245- 249．

(責任編輯 楊 健)

Study on the Dynamic Bound of Shallow Buried and Deep Buried Hydraulic Tunnel and Its Experimental Verification

ZHANG Bi1, Lü Xiaochun2

(1. Shaanxi Railway Institute, Weinan 714000, Shaanxi, China; 2. School of Resources & Environment,North China University of Water Resources and Electric Power, Zhengzhou 450011, Henan, China)

The dynamic bound of shallow buried and deep buried hydraulic tunnel is the intrinsic characteristics of tunnel structure, which is affected by surrounding rock types, tunnel structure shapes, tunnel span and others, and not affected by external factors (such as the type of seismic wave). The calculation and shaking table test show that, the dynamic bound values of shallow buried and deep buried tunnel are strongly influenced by rock type, the rectangular tunnel has big sensitivity and in contrary the circular tunnel has small one, and the tunnel span has a certain influence on dynamic bound values．

tunnel; dynamic bound; shaking table test; seismic wave

2016- 03- 03

國家自然科學基金資助項目(81408222)

張碧(1979—)，男，山西沁縣人，副教授，碩士，主要從事道路與鐵道工程專業的教學和研究工作．

TV312

A

0559- 9342(2016)06- 0026- 04