聯合的平動和轉動相位自聚焦方法

張榆紅,邢孟道,2

(1.西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071; 2.西安電子科技大學信息感知協同創新中心,陜西西安 710071)

聯合的平動和轉動相位自聚焦方法

張榆紅1,邢孟道1,2

(1.西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071; 2.西安電子科技大學信息感知協同創新中心,陜西西安 710071)

在高分辨逆合成孔徑雷達成像中,目標的轉動會在回波信號中引入時變的多普勒調制,導致距離空變的相位誤差,同時傳統的平動相位誤差補償也會因沒有考慮轉動相位誤差而性能嚴重下降.因此,提出了一種聯合的相位自聚焦方法,實現對平動和轉動的相位誤差的聯合校正.首先根據最小熵準則將聯合相位誤差轉化為距離非空變和距離空變的相位誤差,然后運用基于擬牛頓的坐標梯度下降法實現對最小熵優化問題的求解.

逆合成孔徑雷達;聯合相位誤差校正;最小熵;坐標梯度下降法

逆合成孔徑雷達(Inverse Synthetic Aperture Radar,ISAR)由于能夠全天時、全天候地實現對非合作運動目標的二維成像,在軍事和民用領域得到越來越廣泛的應用.一般情況下,逆合成孔徑雷達依靠發射寬頻帶信號獲得距離維高分辨,而方位維高分辨則依賴于目標相對于雷達的轉動[1].在逆合成孔徑雷達成像中,目標運動通常可分解為平動和轉動兩個分量,其中平動由于會引入包絡偏移和相位誤差而導致逆合成孔徑雷達圖像模糊,需要被補償掉[2-3],而轉動由于會產生多樣的多普勒調制,對方位成像有用.然而,轉動會導致越單元徙動(Migration Through Resolution Cells,MTRC),其在距離維表現為空變的距離偏移,在方位維則表現為時變的多普勒調制[3],且隨著分辨率的提高,越單元徙動現象表現得更加明顯.

平動補償可以被分解為距離維和方位維的越單元徙動校正,近年來已經有很多有效的平動補償算法被提出來[4],其中keystone算法由于不需要考慮目標的轉動成為距離維越單元徙動校正的經典方法[5].方位維越單元徙動校正算法則包括時頻分析法[6]、調頻分解法、轉動參數估計算法等.需要注意的是,現有的很多方法均假設已成功實現平動補償,會導致平動補償后的殘余相位誤差被忽略,同時轉動引入的相位誤差也會降低平動補償的性能,因此傳統的平動相位補償后的殘余相位誤差很難被忽略.筆者提出了一種聯合的相位自聚焦方法,實現對平動和轉動的相位誤差聯合校正.首先采用傳統的平動補償方法對回波信號進行處理,接著將平動補償后殘余的平動相位誤差和轉動相位誤差轉化為距離非空變和距離空變的相位誤差,并根據最小熵準則構建目標函數,然后運用基于擬牛頓的坐標梯度下降法對最小熵優化問題進行求解.

1　逆合成孔徑雷達信號模型

如圖1所示,雷達到目標中心O的視線方向定義為Y軸.為了方便后續處理,將目標的轉動分解為兩個正交的方向,其中一個是繞Y軸的方向,另外一個是繞Z軸的方向.需要注意的是,目標沿Y軸的轉動并不改變雷達和各散射點之間的斜距,對逆合成孔徑雷達成像是無用的信息.相反,目標繞Z軸的轉動能夠產生多樣的多普勒分布,是有用分量.在笛卡爾坐標系中,通過右手螺旋準則可以確定坐標軸X的方向.假設目標在相干積累時間內以恒定速度ωz繞Z軸轉動,則在方位維tm時刻目標的轉動角度θ(tm)= ωz·tm.對于位于目標上的散射點p(xp,yp),其與雷達的瞬時斜距可以表示為

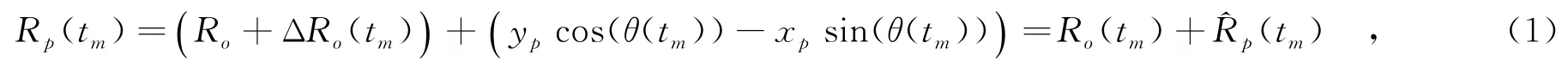
圖1　逆合成孔徑雷達成像幾何模型

其中,Ro為初始時刻雷達到目標中心的斜距;ΔRo(tm)和p(tm)分別表示由目標的平動和轉動所引起的距離變化;Ro(tm)為tm時刻雷達到目標中心的瞬時斜距,且其對所有散射點都是相同的.可以看出,p(tm)對不同的散射點呈現出空變特性.然后,對p(tm)進行泰勒級數展開:

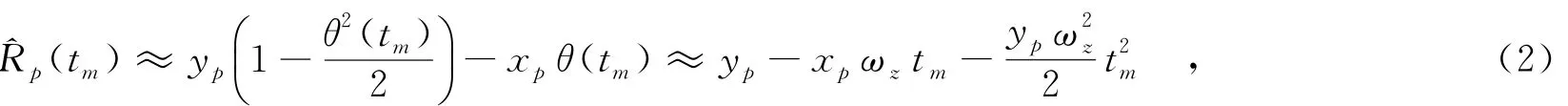
其中,cos(θ(tm))≈1-θ2(tm)/2,sin(θ(tm))≈θ(tm).在式(2)中忽略了二次以上的高次項.由式(2)可知,線性頻率的多普勒調制與目標的轉動速度有關.

假設雷達發射線性調頻信號,通過基帶檢波和距離脈沖壓縮處理后的回波信號可以表示為

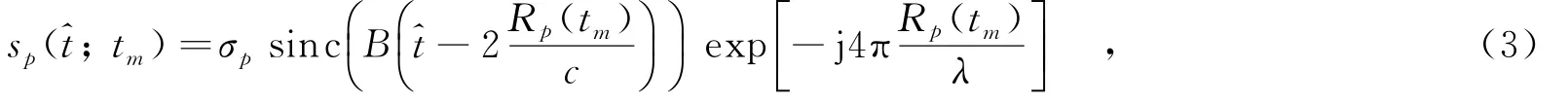
其中,σp為散射點p的散射系數;B、fc和λ分別表示發射信號帶寬、載頻和波長;為距離維快時間;c為光速.將式(1)和(2)代入式(3),可得

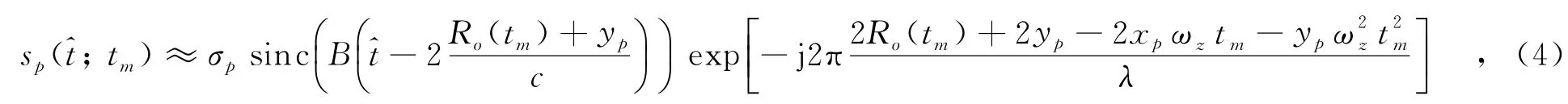
其中,sinc(·)和exp(·)分別對應回波的包絡和相位項.在包絡項中,假設轉動并沒有引起越單元徙動,忽略線性和高次的距離誤差項.在相位項中,由于高分辨成像,考慮因轉動引入且無法忽略的二次相位誤差項,詳細的分析可見文獻[7].

對式(4)中的回波信號進行平動補償來消除由平動引入的包絡偏移和相位誤差.在通常情況下,常規的包絡對齊技術可以實現精確的距離誤差校正,但二次相位誤差對傳統的自聚焦方法提出了挑戰.包絡對齊后,式(4)可以轉化為

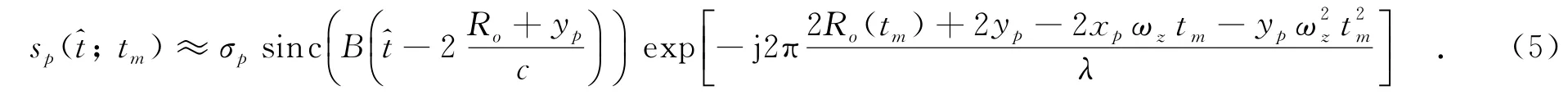
將式(5)離散化表示為

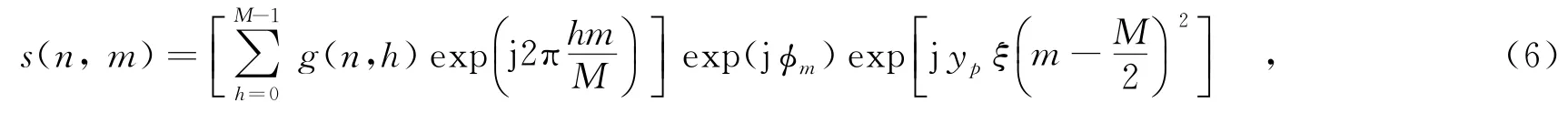
其中,g(n,h)為逆合成孔徑雷達圖像的第(n,h)個像素;M為方位維離散點數;?m=-4πΔRo(tm)λ,表示第m個脈沖的平動相位誤差;表示脈沖重復頻率(Pulse Repetition Frequency,PRF);最后一項為轉動引入的距離空變的相位誤差.

2　聯合的平動和轉動相位誤差補償

由機動目標轉動所引入的距離空變的相位誤差嚴重地降低了平動相位誤差校正的性能,使得傳統的自聚焦方法不再適用.筆者提出了一種基于最小熵準則的機動目標聯合相位自聚焦方法,同時對由平動和轉動引起的距離非空變和距離空變的相位誤差實現更精確的補償.

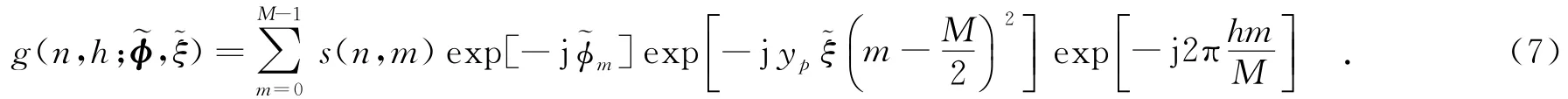
在通常情況下,一幅聚焦良好的逆合成孔徑雷達圖像與模糊的圖像相比具有更小的熵值,即逆合成孔徑雷達圖像的熵值越小,其對應的圖像質量也就越好.因此,在雷達成像中可以將圖像的熵值作為評價相位誤差校正精度的指標.相應地,相位誤差估計的目標函數可表示為

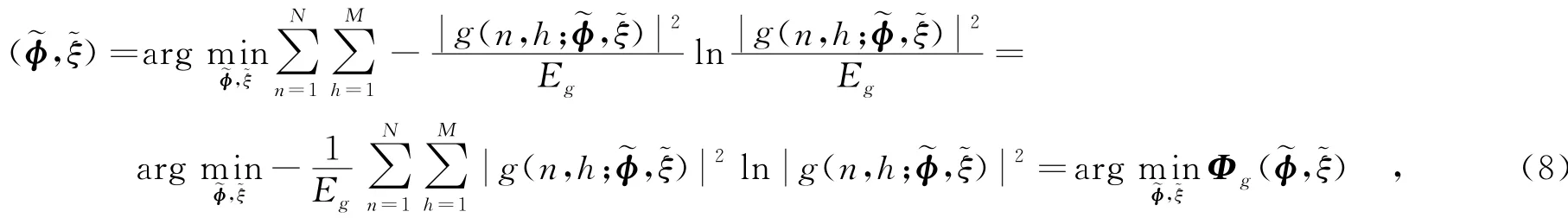
為了求解該問題,已經有很多算法被提出來,包括梯度法、遺傳算法以及窮盡搜索算法等.由式(8)可知,該問題是一個多未知參數的最優化問題,為了確保算法求解的收斂性和高效性,筆者提出了一種基于擬牛頓的坐標梯度下降法,即在一次求解過程中,假設和中的其他參數固定,僅僅估計其中某個參數,并以這樣的方式迭代地估計和中剩余的每一個未知參數.此外,對所有參數的一次遍歷估計等價于一次梯度下降的過程.整個算法可分為3步:

第1步 由于在式(4)中轉動相位誤差僅占據相位誤差的一小部分分量,而平動相位誤差占據絕大部分分量,因此為了避免平動相位誤差對轉動相位誤差估計的嚴重干擾,提高收斂速度,首先采取常規的相位自聚焦方法對回波信號進行平動相位誤差粗校正[8-9],使得殘余的平動相位誤差不是很嚴重.

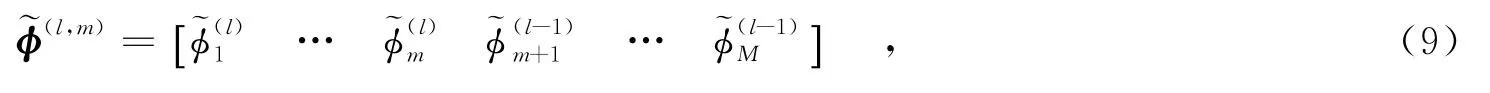
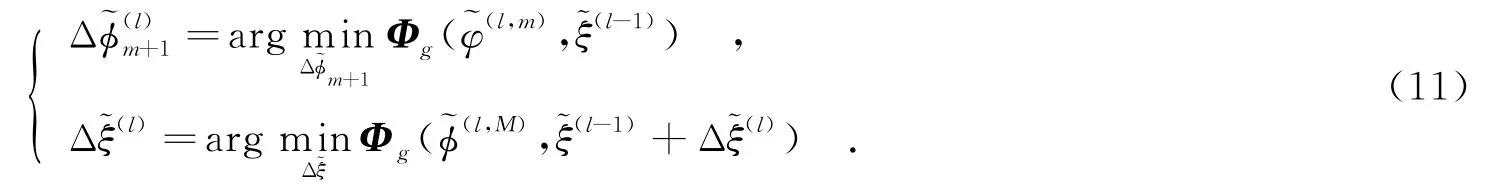
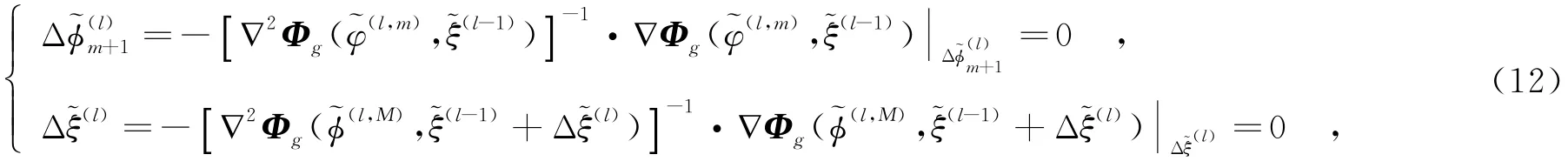
3　仿真數據處理的結果及其分析

仿真實驗采用的Yak-42飛機由330個散射點組成,其距離維和方位維尺寸大小分別為42.00 m× 38.25 m.該系統仿真參數如表1所示,且在相干處理時間內,目標的轉動速度恒為0.028 rad/s.通過計算可知,由轉動所引入的二次相位誤差絕對值的最大值為21.697 7 rad,在成像中很難被忽略.需要注意的是,由目標或雷達平臺的劇烈振動所引入的隨機相位誤差很難被校正[10-11],此處考慮高次多項式加隨機的平動相位誤差來評估筆者提出算法的性能,且添加的平動相位誤差如圖2所示.

表1　仿真參數

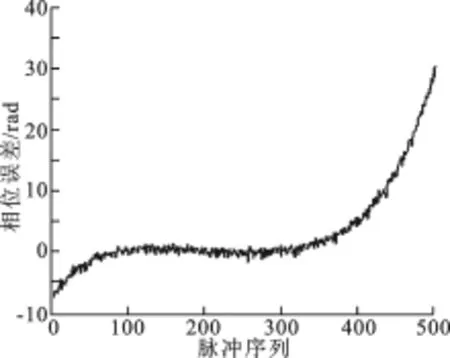
圖2　添加的相位誤差

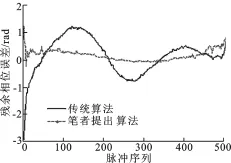
圖3　殘余相位誤差

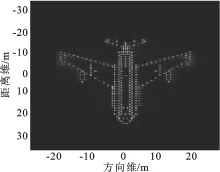
圖4　傳統自聚焦逆合成孔徑雷達圖像

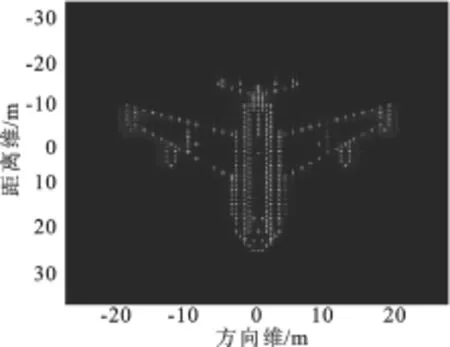
圖5　筆者提出算法的逆合成孔徑雷達圖像

假設對回波信號已經完成包絡對齊和越單元徙動校正,然后采用傳統的自聚焦方法,即最小熵方法對回波信號進行平動相位誤差校正,其殘余的平動相位誤差如圖3中的實線所示.由圖3可以看出,殘余的平動相位誤差大于π/4,很難被忽略.然后,采用筆者提出的方位同時對殘余的平動和轉動相位誤差進行校正,并計算校正后的殘余平動相位誤差,其結果如圖3中的虛線所示.可以看出,與傳統的最小熵自聚焦方法相比,筆者提出的方法能夠有效地提高相位誤差校正的性能,且殘余的平動相位誤差均小于π/4.接著,采用文獻[9]中所提出的方法對目標的轉動速度進行估計,并采用估計得到的轉動速度進行方位維定標,其結果分別如圖4和圖5所示.圖4為傳統自聚焦方法得到的定標逆合成孔徑雷達圖像,圖5表示筆者提出算法得到的定標逆合成孔徑雷達圖像,可以看出筆者提出的算法能夠實現更好的聚焦性能,實現更高質量的逆合成孔徑雷達成像.同時,計算得到圖4和圖5的熵值分別為8.063 1和7.443 7,也驗證了筆者提出的算法的有效性.

4　總 結

筆者對高分辨逆合成孔徑雷達成像的運動補償問題進行了研究,提出了一種聯合的平動和轉動相位自聚焦方法.文中總的相位誤差可表示為非距離空變和距離空變的相位誤差之和,將相位誤差的校正問題轉化為基于最小熵的最優化問題,并采用坐標梯度下降法進行求解.最后,通過仿真數據實驗驗證了筆者提出算法的有效性.

[1]CHEN V C,MARTORELLA M.Inverse Synthetic Aperture Radar Imaging[M].Edison,NJ:SciTech Publishing,2014.

[2]ZHU D Y,WANG L,YU Y S,et al.Robust ISAR Range Alignment via Minimizing the Entropy of the Average Range Profiles[J].IEEE Geoscience and Remote Sensing Letters,2009,6(2):204-208.

[3]THOMAS K J,ALAA K A.Monotonic Iterative Algorithm for Minimum-entropy Autofocus[C]//IEEE International Conference on Image Processing:5.Piscataway:IEEE,2006:645-648.

[4]LUG Y,BAO Z.Compensation of Scatter Migration through Resolution Cell in Inverse Synthetic Aperture Radar Imaging[J].IEE Proceedings-Radar,Sonar and Navigation,2000,147(2):80-85.

[5]XING M D,WU R B,LAN J Q,et al.Migration through Resolution Cell Compensation in ISAR Imaging[J].IEEE Geoscience and Remote Sensing Letters,2004,1(2):141-144.

[6]CHEN V C,MICELI W J.Time-varying Spectral Analysis for Radar Imaging of Maneuvering Targets[J].IEE Proceedings-Radar,Sonar and Navigation,1998,145(5):262-268.

[7]XU G,XING M D,ZHANG L,et al.Sparse-apertures ISAR Imaging and Scaling for Maneuvering Targets[J].IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing,2014,7(7):2942-2956.

[8]徐剛,楊磊,張磊,等.一種加權最小熵的ISAR自聚焦算法[J].電子與信息學報,2011,33(8):1809-1815. XU Gang,YANG Lei,ZHANG Lei,et al.Weighted Minimum Entropy Autofocus Algorithm for ISAR Imaging[J]. Journal of Electronics&Information Technology,2011,33(8):1809-1815.

[9]黃大榮,張磊,邢孟道,等.機動目標ISAR自聚焦新方法[J].西安電子科技大學學報,2014,41(3):71-78. HUANG Darong,ZHANG Lei,XING Mengdao,et al.ISAR Autofocus Method for Maneuvering Targets[J].Journal of Xidian University,2014,41(3):71-78.

[10]陳倩倩,邢孟道,李浩林,等.一種適用于低信噪比短CPI的ISAR橫向定標算法[J].西安電子科技大學學報,2014,41 (6):12-17. CHEN Qianqian,XING Mengdao,LI Haolin,et al.Cross-range Scaling for ISAR Imaging within Short CPI and Low SNR[J].Journal of Xidian University,2014,41(6):12-17.

[11]SHENG J L,XING M D,ZHANG L,et al.ISAR Cross-range Scaling by Using Sharpness Maximization[J].IEEE Geoscience and Remote Sensing Letters,2015,12(1):165-169.

(編輯:郭 華)

Approach to joint translational and rotational phase auto-focusing

ZHANG Yuhong1,XING Mengdao1,2
(1.National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China;2.Collaborative Innovation Center of Information Sensing and Understanding,Xidian Univ.,Xi’an 710071,China)

In high-resolution inverse synthetic aperture radar imaging,the rotational motion of the targets tends to introduce the time-variant Doppler modulation in the echo,which acts as the range-variant phase errors in phase history.Moreover,the performance of translational phase error compensation may be dramatically degraded without properly considering the range-variant phase errors.In this paper,an approach to joint translational and rotational phase auto-focusing is proposed.In the procedure,the joint phase error correction is modeled as range-invariant and range-variant phase errors using a metric of minimum entropy.Then the minimum-entropy optimization is solved by employing a coordinate descend method based on the quasi-Newton solver.Finally,experiment based on simulated data is performed to confirm the effectiveness of the proposed algorithm.

inverse synthetic aperture radar(ISAR);joint phase error correction;minimum entropy; coordinate descend method

TN957

A

1001-2400(2016)05-0031-05

10.3969/j.issn.1001-2400.2016.05.006

2015-07-09 網絡出版時間:2015-12-10

國家自然科學基金資助項目(61301280)

張榆紅(1987-),女,西安電子科技大學博士研究生,E-mail:xiaoshan198717@163.com.

網絡出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.012.html