一種改進的復延遲時頻分布算法

江 莉,趙國慶,李 林

(1.西安電子科技大學電子工程學院,陜西西安 710071; 2.西安建筑科技大學信息與控制工程學院,陜西西安 710055)

一種改進的復延遲時頻分布算法

江 莉1,2,趙國慶1,李 林1

(1.西安電子科技大學電子工程學院,陜西西安 710071; 2.西安建筑科技大學信息與控制工程學院,陜西西安 710055)

針對計算復延遲信號時存在計算機精度不夠、甚至溢出的問題,提出了一種改進算法.該算法通過頻譜遞推估計和信號尺度變換,有效解決了復延遲時頻分布的算法實現問題.仿真實驗表明,改進算法相比原始算法具有較好的噪聲抑制能力和時頻能量聚集性.

復延遲時頻分布;復延遲信號;時頻能量聚集性

時頻分布又稱時頻表示,是非平穩信號分析的一個重要手段,可得到信號頻率隨時間變化的分布特征[1-2].傳統的時頻表示分為兩類[3]:一類是線性時頻表示,由傅里葉變換轉化而來,如短時傅里葉變換(Short-Time Fourier Transform,STFT)、小波變換等;另一類是二次型時頻表示,又稱雙線性時頻分布,如Wigner-Ville分布(Wigner-Ville Distribution,WVD)、Choi-Williams分布(Choi-Williams Distribution,CWD)[4]等.線性時頻表示無交叉項干擾,但時頻聚集性較差.二次時頻分布在一定程度上提高了時頻聚集性,但受交叉項干擾嚴重.針對自然界和工程應用中廣泛存在的非線性、非平穩信號,高階時頻分布[5]近年來得到人們的廣泛關注.在Cohen類二次時頻分布的基礎上,文獻[6]提出的一種新型的高階時頻分布,即復延遲時頻分布(Complex-Time Distribution,CTD),對于非線性連續頻率調頻信號,CTD具有優良的時頻聚集性[7-8].計算CTD時,需要通過傅里葉變換及反變換計算復延遲信號,指數變化的幅度因子導致計算機數據精度不夠,甚至溢出,從而影響算法性能.算法實現問題一直是CTD的一個難點,制約著其在實際工程中的應用.基于此問題,筆者以4階CTD為例,提出了一種基于頻點遞推的復延遲信號計算方法,避免了計算復延遲信號的計算機精度及溢出問題.并針對噪聲干擾,提出了一種基于信號尺度變換的復延遲信號計算方法.

1　復延遲時頻分布

假設解析信號s(t)=A exp(j?(t)),于是,可定義L階復延遲時頻分布為[9]

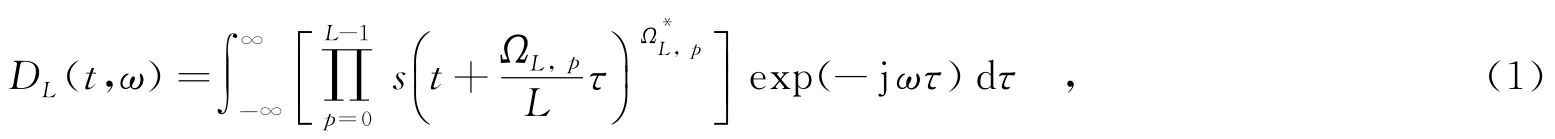
其中,ΩL,p=exp(j2πpL),為復數延遲,可通過傅里葉反變換進行計算,即

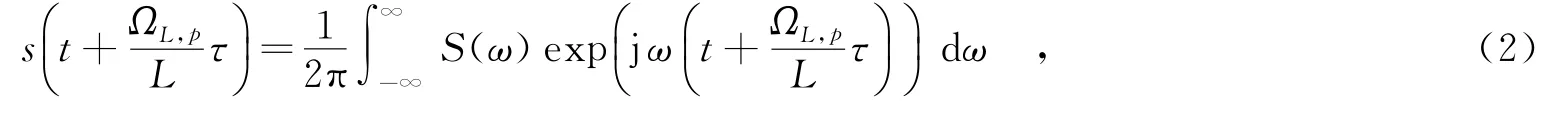
其中,S(ω)為信號s(t)的頻譜.

一般情況下CTD的階數L為偶數,最常用的為4階,則4階CTD可表示

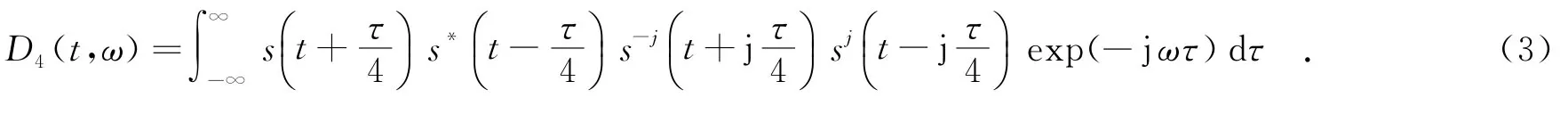
4階CTD的時頻擴展因子為

理論上,CTD的階數越高,時頻聚集性越好.實際中由于信號調制復雜并存在多個分量,復延遲時頻分布的自交叉項和互交叉項干擾會隨階數的增加而變得更加嚴重.可將L階CTD用另外一種方式表示為

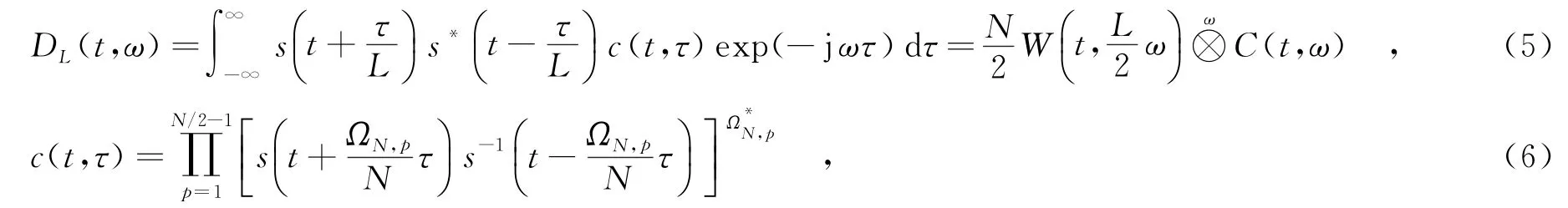
其中,c(t,τ)是瞬時自相關的修正項,C(t,ω)是c(t,τ)的傅里葉變換,C(t,ω)可看作頻域濾波器,表示對ω進行卷積,W(t,ω)表示WVD.式(5)中,CTD可看作是一種加了核的WVD,而式(6)為核函數.

考慮到實際處理的信號為離散形式,D4的離散計算公式為

利用傅里葉反變換計算信號的復延遲,離散公式可表示為

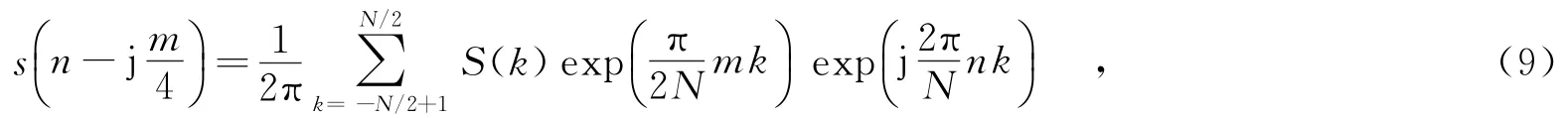
其中,S(k)為信號s(n)的離散傅里葉變換.可見,幅度因子exp(πmk(2N))隨mk呈指數變化,當mk較大時,幅度因子趨于0或無窮大,會導致計算機數據精度不夠,甚至溢出.算法實現問題一直是CTD的一個難點.

圖1　幅度修正后的信號幅頻特性圖

圖1為經過幅度因子修正后的信號幅頻特性圖.仿真信號為線性調頻信號,并疊加信噪比為20 dB的高斯白噪聲,信號采樣點數N=256.圖1(a)中m=0,即原始信號的幅頻特性圖;圖1(b)和(c)分別對應m=32和m=-32.可以看出,當m＞0時,幅度因子導致信號頻率正半軸指數增加,而負半軸指數減小;當m＜0時,情況正好相反.幅度因子極大地增加了頻率數值的動態范圍,從而導致計算機數據精度不夠,甚至溢出.在現有的有關離散信號CTD研究中,僅針對采樣點數較短情況(例如N≤128)進行分析[10].

2　改進算法

2.1基于頻點遞推的復延遲信號計算方法

針對CTD的實現問題,文中提出一種遞推算法.這里主要針對D4,其他更高階的CTD可參考D4實現.首先,式(9)可改寫為

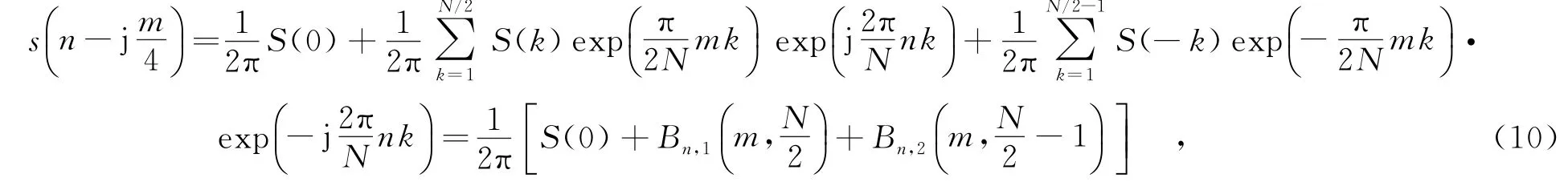
其中,Bn,1和Bn,2分別表示式(10)中的后兩部分求和.Bn,1的遞推公式可表示為

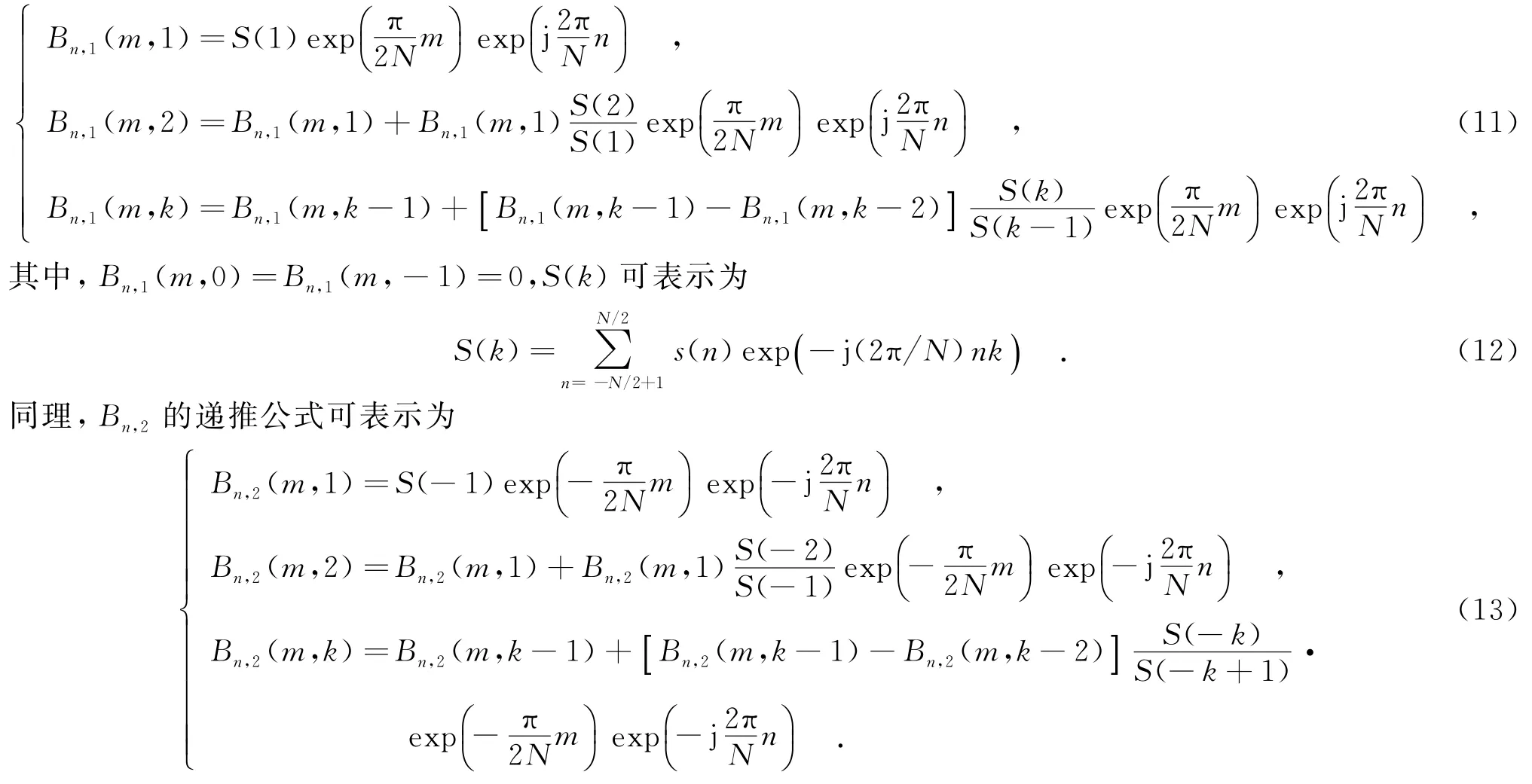
利用上述的遞推公式可解決復延遲的計算機精度及溢出問題,也使其可分析采樣點數更長的信號.對于任意復數z的虛數次冪,可表示為

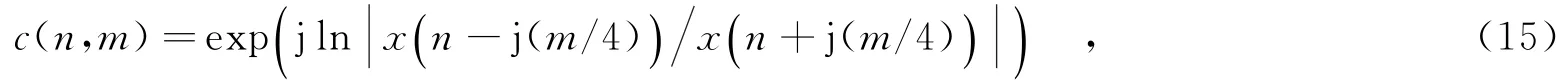
當m=0時,有c(n,m)=1.

2.2噪聲抑制方法

以圖1為例,如果分析信號中存在噪聲,那么由于指數幅度因子會放大噪聲的影響,從而導致復延遲信號產生較大誤差.同時,當分析信號的帶寬較寬或中心頻率較高時,指數幅度因子對信號的影響更大.帶內的小噪聲將會被指數量級放大,增強了噪聲頻率分量.因此,這里提出一種信號尺度變換方法.

考慮信號s(at),a＞1.針對復延遲信號s(at+j aτ),應用泰勒級數展開,即

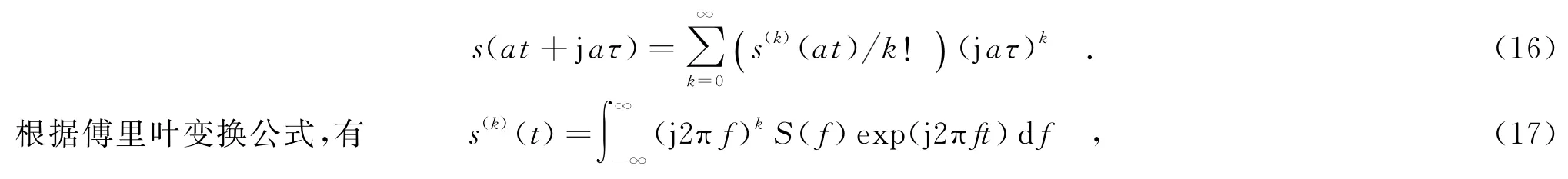
其中,S(f)為s(t)的傅里葉變換,經推導可得

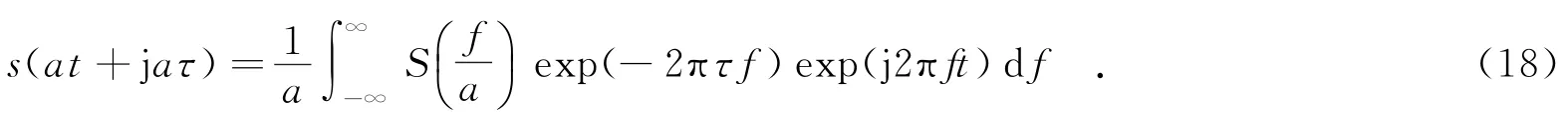
可以看出,上式相當于提高了頻譜的聚集性,使得計算復延遲時受幅度因子exp(-2πτf)的影響變小.將上述思想應用到截獲的離散信號s(n),假設a=2,先對信號進行兩倍插值,計算插值信號的頻譜S2N(k),再利用式(9)和式(18)計算復延遲.利用2.1節提出的遞推算法,解決了插值后信號采樣點數增加情況下CTD的實現問題,保證了計算精度.為進一步抑制帶外噪聲,可考慮對頻譜進行加窗,這里采用高斯窗.高斯窗函數適合于非周期指數信號,在一定程度上抑制指數幅度的影響.

3　仿真實驗及結果分析

首先比較上節中提出的D4改進算法與原始算法在計算復延遲信號時的差異.仿真信號為線性調頻信號,信號參數與圖1相同,信號采樣點個數為256點,延遲量m=-4.圖2(a)和(b)是原始算法的計算結果,圖2(c)和(d)是改進算法的計算結果.可以看出,無噪聲時在數據兩端由于加權幅度因子較大,如圖1(c)所示,直接利用原始算法計算復延遲信號時會受計算精度影響.對比圖2(a)和(c)可以看出,遞推算法有效解決了復延遲信號的計算問題.信號復延遲受噪聲影響很大,原始算法幾乎無法應用.如圖2(b),當信噪比為8 d B(高斯白噪聲)時,原始算法對復延遲信號的估計產生了較大的偏差.對比圖2(b)和(d)可以看出,改進算法通過頻譜壓縮,可較好抑制噪聲的影響,使噪聲受到指數幅度因子加權而產生的干擾大大降低.

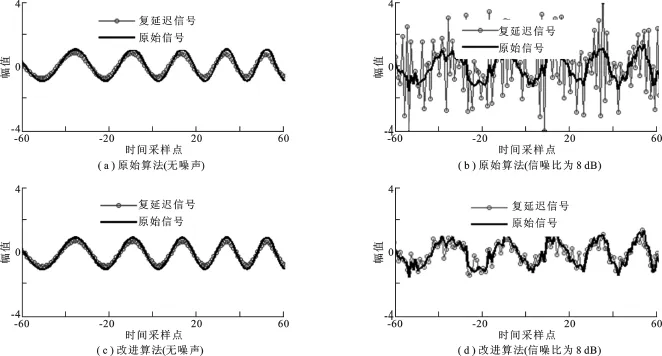
圖2　噪聲對復延遲信號影響的比較圖

下面的實驗中利用復延遲時頻分布分析非平穩信號.為了驗證復延遲時頻分布的時頻聚集性,選擇非線性連續頻率調制信號,該類信號廣泛應用于雷達、通信等實際系統中.考慮到原始D4算法在數據采樣點較多時容易導致計算機溢出,本實驗中信號采樣點個數為128.圖3(a)和(b)分別為譜圖(短時傅里葉變換的模平方)和WVD的時頻分布計算結果.譜圖時頻分辨率較差,WVD受交叉項影響較大,兩種時頻分析方法均無法精確表示信號的瞬時頻率變換特征.圖3(c)和(d)分別是原始D4和改進D4的計算結果.對于仿真信號,D4的時頻能量聚集性要明顯優于譜圖和WVD的.改進D4算法也優于原始D4的,不但抑制了交叉項,也具有更高的時頻聚集性.

圖3　不同時頻分析算法的比較圖

4　結束語

通過頻譜遞推估計和信號尺度變換,有效解決了復延遲時頻分布的算法實現問題.仿真實驗證明,改進算法相比原始算法具有較好的噪聲抑制能力和時頻能量聚集性.然而,高階時頻分布(包括D4)的計算量較大,文中提出的迭代算法計算效率有限,需要進一步進行算法優化.此外,高階時頻分布對噪聲的魯棒性較差,需要進一步研究低信噪比下的改進算法.

[1]SEJDIC E,DJUROVIC I,JIANG J.Time-frequency Feature Representation Using Energy Concentration:an Overview of Recent Advances[J].Digital Signal Processing,2009,19(1):153-183.

[2]LI L,JIANG L.Recognition of Polyphase Coded Signals Using Time-frequency Rate Distribution[C]//2014 IEEE Workshop on Statistical Signal Processing.Piscataway:IEEE,2014:484-487.

[3]IVAN'OVIC V N,DAK'OVIC M,STANK'OVIC L.Performance of Quadratic Time-frequency Distributions as Instantaneous Frequency Estimators[J].IEEE Transactions on Signal Processing,2003,51(1):77-89.

[4]LU J,ORUKLU E,SANIIE J.Improved Time-frequency Distribution Using Singular Value Decomposition of Choi-Williams Distribution[C]//2013 IEEE International Conference on Electro/Information Technology.Piscataway:IEEE,2013:1-4.

[5]SAAD A Q,LAMPROS K S.Higher Order Nested Wigner Distribution:Properties and Applications[J].IEEE Transactions on Signal Processing,2006,54(12):4662-4674.

[6]STANKOVIC L.Time-frequency Distributions with Complex Argument[J].IEEE Transactions on Signal Processing,2002,50(3):475-486.

[7]潘陽.高階時頻分布及其在LPI信號分析中的應用[D].西安:西安電子科技大學,2014.

[8]STANKOVIC S,OROVIC I.An Ideal OMP Based Complex-time Distribution[C]//2nd Mediterranean Conference on Embedded Computing.Washington:IEEE,2013:109-112.

[9]王冉,姜義成.一種針對多分量信號的復延遲型時頻分布的實現方法[J].電子學報,2012,40(1):60-65. WANG Ran,JIANG Yicheng.A Realization of Time-frequency Distributions with Complex-lag Argument for Multicomponent Signal[J].Acta Electronica Sinica,2012,40(1):60-65.

[10]STANKOVIC S,OROVIC I.Robust Complex-time Distributions Based on Reconstruction Algorithms[C]//2nd Mediterranean Conference on Embedded Computing.Washington:IEEE,2013:105-108.

(編輯:齊淑娟)

Modified algorithm for complex-time distribution

JIANG Li1,2,ZHAO Guoqing1,LI Lin1
(1.School of Electronic Engineering,Xidian Univ.,Xi’an 710071,China;2.School of Information and Control Engineering,Xi’an Univ.of Architecture and Technology,Xi’an 710055,China)

Aiming at the problems of computer precision and even overflow,a new modified algorithm is proposed.The complex-time distribution algorithm can be accomplished effectively by frequency spectrum iteration estimation and signal scale conversion.Simulation results show that the proposed method has a good ability to suppress the influence of noise interferences,improve the energy convergence,and provide theoretical and technical support for the enginnering application.

complex-time distribution;complex-lag signal;time frequency energy concentration

TN971

A

1001-2400(2016)05-0036-05

10.3969/j.issn.1001-2400.2016.05.007

2015-09-07 網絡出版時間:2015-12-10

國家自然科學基金資助項目(61201287);中央高校基本科研業務費專項資金資助項目(JB140208);陜西省教育廳專項科研計劃資助項目(16JK1429)

江 莉(1982-),女,西安電子科技大學博士研究生,E-mail:yolanda_jiangli@163.com.

網絡出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.014.html