聚焦《推理與證明》中的九類經典問題
■陜西省洋縣中學 雍 康
?
聚焦《推理與證明》中的九類經典問題
■陜西省洋縣中學 雍 康
推理與證明是在同學們已有知識的基礎上完善了合情推理的兩種方式——納推理和類比推理,以及數學證明的主要方法——分析法、綜合法、反證法等常用方法。上述推理方式和證明方法都是數學的基本思維過程,它們貫穿于整個高中數學的學習,能使同學們通過學習感受邏輯思維方式在數學以及日常生活中的作用。下面聚焦其經典問題,希望能有益于同學們的學習。
聚焦一:函數性質研究中的演繹推理


點評:已知周期函數在給定區間的解析式,可利用周期性和對稱性將所求值化為在已知區間上求值。整個求解過程是從一般到特殊的推理過程,即演繹推理的過程,在大前提、小前提和推理形式都正確的前提下,得到的結論一定正確。
聚焦二:復合函數解析式中的歸納猜測

點評:歸納推理是由部分到整體,由特殊到一般的推理過程。在進行歸納時,通過取特殊值計算出幾個結果,可以發現一般規律,從而做出合理的猜想,即合情推理。本題以復合函數解析式為載體,考查對遞推關系的理解和應用,以及同學們的計算與歸納猜測能力。
聚焦三:“分裂數”中的歸納猜測
例3 (2015年山東淄博市高三模擬)對于大于等于1的自然數m的三次冪可用奇數進行以下方式的“分裂”:13=1,23=3+5,33=7+9+11,43=13+15+17+19,…。仿此,若m3的“分裂數”中有一個是2 015,則m____。

點評:解決這類問題時,首先觀察式子的結構特點,其次觀察式子中出現的字母之間的關系,再進行化簡或運算。另外要注意對較為復雜的運算式,先不要化簡,這樣便于觀察運算規律和結構上的共同點,有時還要借助等差或等比數列的性質簡化求解。
聚焦四:等差與等比數列中的類比推理


證明如下:設等差數列{an}的公差為d。


點評:把等差與等比數列進行類比,運用類比思想找出項與項的聯系,應用等差、等比數列的性質是解決該題的關鍵。等差數列和等比數列有非常類似的運算和性質,一般情況下等差數列中的和(或差) 對應著等比數列中的積(或商)。
聚焦五:圖形關系中的類比



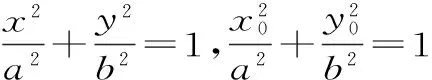




點評:圖形關系中的類比,找兩類對象的對應元素,找對應元素的對應關系,同時注意方法的類比。
聚焦六:數列推理中的綜合法

(1)求a1的值;
(2)求數列{an}的通項公式;



(Sn+3)[Sn-(n2+n)]=0。
因為an>0(n∈N*),所以Sn>0。從而Sn+3>0,所以Sn=n2+n。
當n≥2時,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n。
又a1=2=2×1,所以an=2n(n∈N*)。
(3)對通項公式放縮變形重新改寫,用裂項相消法求和,也可用觀察法證明不等式。

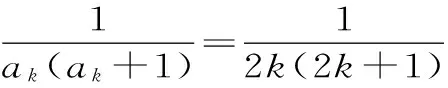
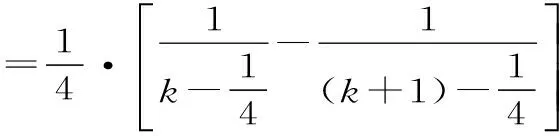



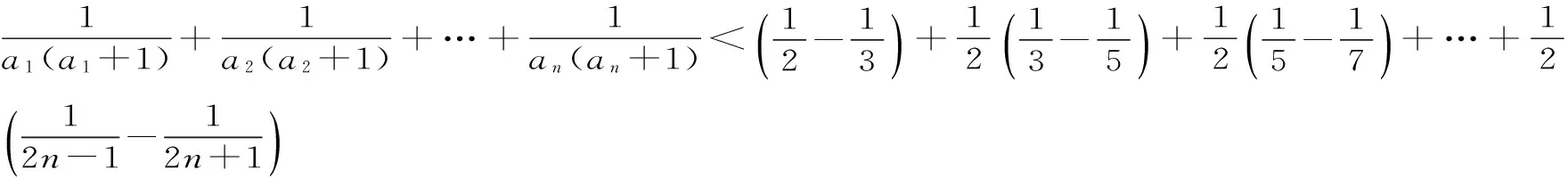

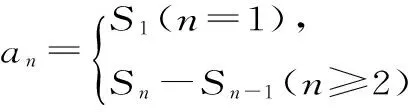
聚焦七:不等式證明中的綜合分析
例7 設a,b,c均為大于1的正數,且ab=10。
求證:logac+logbc≥4lgc。
證明:單一運用綜合法或分析法很復雜,本題若兩者均用,效果更好。
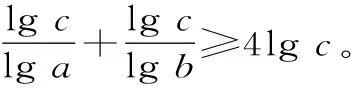
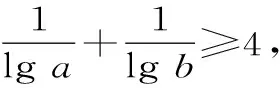
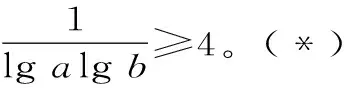
a>1,b>1,故lga>0,lgb>0。

故原不等式得證。
點評:分析法與綜合法各有優勢,證明問題時,可結合使用,先以分析法為主尋求解題思路,再用綜合法有條理地解答或證明。兩者交替使用,較易成功。這種方法不僅在證明不等式時經常用到,在解決其他數學問題時也常常用到。
聚焦八:新定義問題中的合情推理
A.77 B.49 C.45 D.30
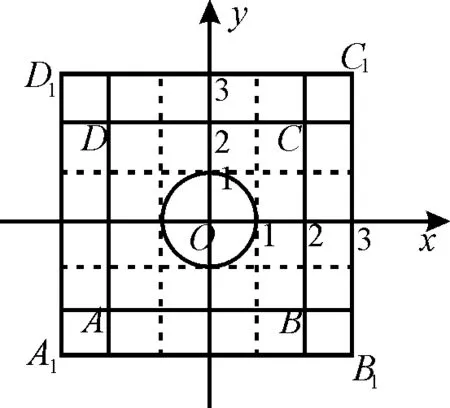
圖1

點評:這是一道與集合相關知識的新定義題型。通過給出一個新定義,或約定一種新運算,或給出幾個新模型來創設全新的問題情景,要求同學們在閱讀理解的基礎上,依據題目提供的信息,聯系所學的知識和方法,結合圖形實現信息的遷移,達到靈活解題的目的。
聚焦九:先猜后證中的數學歸納法
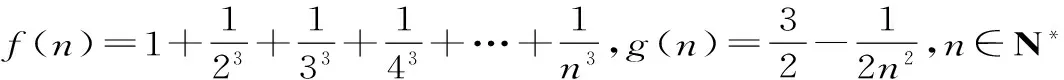
(1)當n=1,2,3時,試比較f(n)與g(n)的大小關系;
(2)猜想f(n)與g(n)的大小關系,并給出證明。
解析:由特殊到一般,先猜再用數學歸納法證明。
(1)當n=1時,f(1)=1,g(1)=1,所以f(1)=g(1)。
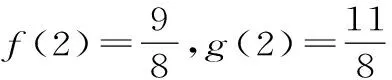
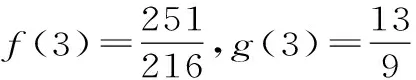
(2)由(1)猜想f(n)≤g(n),下面用數學歸納法給出證明。
①當n=1,2,3時,不等式顯然成立。
②假設當n=k(k≥3,k∈N*)時不等式恒成立,即:

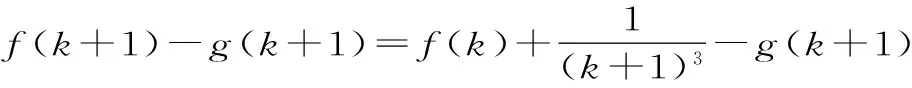

所以f(k+1) 由①、②可知,對一切n∈N*,都有f(n)≤g(n)成立。 (責任編輯 徐利杰)

