聚焦《數系的擴充與復數的引入》中的幾類經典問題

■河南省平頂山市一中 李智恒

?

聚焦《數系的擴充與復數的引入》中的幾類經典問題

■河南省平頂山市一中 李智恒

數系的擴充與復數的引入在高考中以容易或中檔的小題出現，試題具有活而不難的特點，且常考常新。同學們學習時應狠抓基礎，對復數的概念、復數運算等要熟練掌握，還要注意對數形結合思想，復數問題實數化以及方程思想的挖掘和應用。

聚焦一：復數有關概念中的“巧設”和“分類意識”

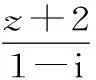
A.2i B.i C.-i D.-2i

(2)(2015年河北衡水中學調研卷)z1=-4a+1+(2a2+3a)i,z2=2a+(a2+a)i,其中實數a∈R,z1>z2,則a的值是____。

(2)依據兩個實數才能比較大小構建方程和不等式組確定參數范圍。

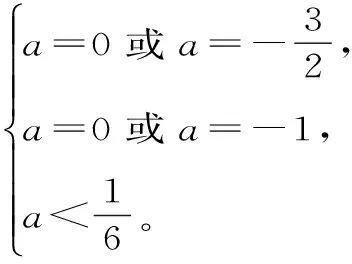
點評：由實數擴充到復數后,實數系的有些性質、運算法則對于復數系并不適用,故解答復數問題時要依據復數的概念合理進行轉化，不能輕易地將實數系中的一些運算法則或性質照搬到復數系內。如當兩個復數都是實數時,可以比較大小;兩個虛數或一個虛數與一個實數不能比較大小。

聚焦二：利用復數相等的充要條件化虛為實

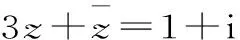
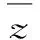
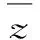
聚焦三：復數運算中的“分母實數化”

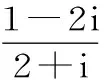
解析：分母實數化。

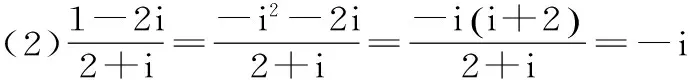
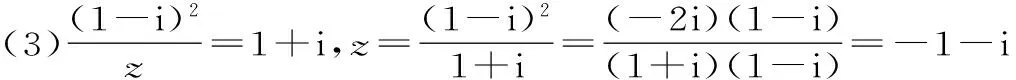
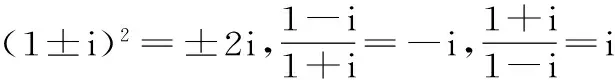
聚焦四：利用共軛復數的性質整體求解復數

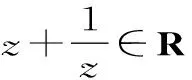
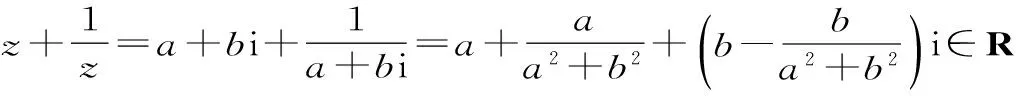
當b=0時，z=a，|a-2|=2，則a=0或4。當a=0時不合題意舍去，所以z=4。

當b≠0時，a2+b2=1。

又|z-2|=2，則：

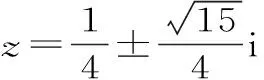
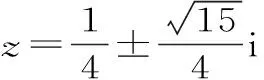
解法2： 利用共軛復數的性質。

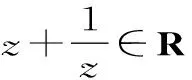
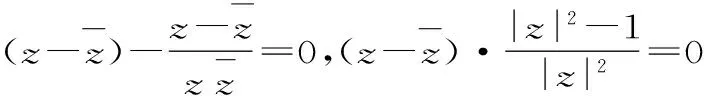
聚焦五：數形結合法探究模的最值

例5 設復數滿足||z+4-3i|-2|=2-|z+4-3i|，求|z|的最大值和最小值。

解析：觀察分析等式||z+4-3i|-2|=2-|z+4-3i|，根據實數的性質知，若|a|=-a，則a≤0。

因此，|z+4-3i|-2≤0。

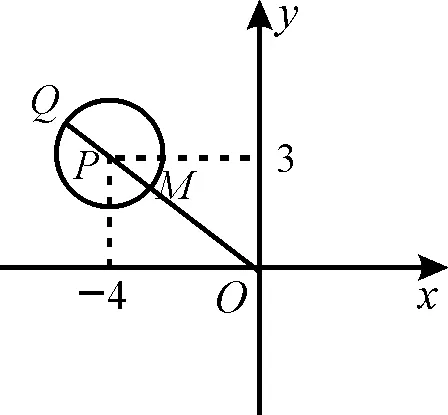
圖1

挖掘|z+4-3i|-2≤0的幾何意義，它表示的以點P(-4，3)為圓心，半徑為2的圓及內部。如圖1，可知 |z|=|OQ|時，|z|有最大值，|z|max=|OQ|=|OP|+R=5+2=7；

|z|=|OM|時，|z|有最小值，|z|min=|OM|=|OP|-R=5-2=3。

點評：復數既可用代數形式，也可用幾何形式表示。這使復數的各種運算都具有了幾何意義，因此，求解復數問題時常以形助數，數形結合，使問題的解決更加形象。求復數模的最值常常根據其幾何意義，利用圖形可直接來解。

聚焦六：用函數與方程思想求模的最值

例6 已知關于x的方程x2+zx+4+3i=0有實數根，求復數z的模的最小值。

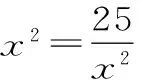
點評：復數系方程有實根，不能得出Δ=z2-16-12i≥0，只說明x可以取實數時，復數系一元二次方程不能用判別式來判斷方程是否有實根。方程有解的問題要注意系數的范圍，當題設條件不特別說明時系數均為復數，處理方程問題的有效途徑是巧設代數形式，利用根的意義，借助兩個復數相等的充要條件構建方程組，化歸到實數中的問題求解。

聚焦七：復數與簡易邏輯的網絡交匯

例7 (1)(2015年高考上海理科數學)設z1，z2∈C，則“z1、z2中至少有一個數是虛數”是“z1-z2是虛數”的( )。

A．充分不必要條件

B．必要不充分條件

C．充要條件

D．既不充分又不必要條件

(2)(2014年高考陜西卷)原命題為“若z1,z2互為共軛復數，則|z1|=|z2|”，關于其逆命題，否命題，逆否命題真假性對應的判斷依次如下，正確的是( )。

A.真，假，真 B.假，假，真

C.真，真，假 D.假，假，假

解析：(1)利用復數概念合理分類研究，借助四種命題之間的關系簡化判斷。若z1、z2皆是實數，則z1-z2一定不是虛數，因此當z1-z2是虛數時，則“z1、z2中至少有一個數是虛數”成立，即必要性成立；當z1、z2中至少有一個數是虛數，z1-z2不一定是虛數，如z1=z2=i，即充分性不成立，選B。

點評：高考對復數的考查越來越深入，特別是復數與簡易邏輯的有機結合應引起同學們的高度重視。復數分類與充要條件的判斷，以及對形如a+bi(a，b∈R)的復數的認知，其中a，b分別是它的實部和虛部。若b=0，則a+bi為實數；若b≠0，則a+bi為虛數；若a=0且b≠0，則a+bi為純虛數。判斷命題的真假必須從其定義出發，不可想當然。 互為共軛復數與其模之間的關系構成的四種命題的判斷，依據概念只需判斷原命題和逆命題的真假即可。

聚焦八：復數與新定義的交匯

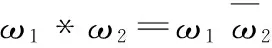
①(z1+z2)*z3=(z1*z3)+(z2*z3);

②z1*(z2+z3)=(z1*z2)+(z1*z3)；

③(z1*z2)*z3=z1*(z2*z3);

④z1*z2=z2*z1。

則真命題的個數是( )。

A．4 B．3 C．2 D．1

對于②，直接用定義，設復數的代數形式，利用分配律和復數運算結合定義驗證：

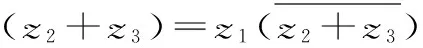
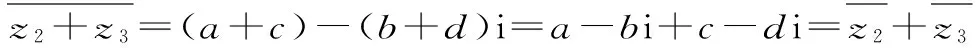
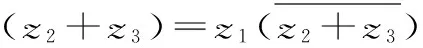
=z1*z2+z1*z3。

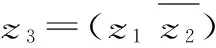
故(z1*z2)*z3≠z1*(z2*z3)。

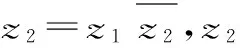
點評：新定義與復數概念運算相結合的創新問題，依據新定義的意義結合復數的概念運算以及運算規律進行驗證，涉及復數乘法和加法的結合律和共軛復數的整體性質。

(責任編輯 徐利杰)