隨機需求環境下零售商聯合采購與合并運輸聯盟的穩定性分析

肖 旦，劉 芳，史欣向，秦隴一

（廣州大學 工商管理學院，廣東 廣州 510006）

隨機需求環境下零售商聯合采購與合并運輸聯盟的穩定性分析

肖 旦，劉 芳，史欣向，秦隴一

（廣州大學 工商管理學院，廣東 廣州 510006）

在隨機需求環境下，企業為了降低運作成本，會進行聯合采購與合并運輸的戰略合作，但是，為了維持所形成合作聯盟的穩定性，必須公平合理地分攤聯盟的總運作成本.文章采用合作博弈論中的核概念，對隨機需求環境下零售商聯合采購與合并運輸聯盟的穩定性展開了分析.①http：//news.cnnb.com.cn/system/2012/09/21/007467919.shtml在需求隨機到達的情形下，得到了零售商聯合采購與合并運輸聯盟的最優訂貨策略；②http：//news.dichan.sina.com.cn/2015/11/01/1132694.html指出零售商進行聯合采購與合并運輸的戰略并不一定總能降低聯盟的總期望運作成本，由此提出了零售商合作能降低總期望運作成本的條件；③在可降低總期望運作成本的條件下，提出了按邊際成本進行分攤的規則可使大聯盟保持穩定，并通過一個具體的實例對成本分攤方案進行了說明.

隨機需求；合并運輸；訂貨量；穩定性

采購是企業運作中非常重要的一個環節，據中國物流與采購聯合會公布的2012年采購調查數據顯示，企業的采購成本占總銷售收入的55%①http：//news.cnnb.com.cn/system/2012/09/21/007467919.shtml.因此，如何降低企業的采購成本，一直是學術界和企業經理人所關心的熱點問題.近年來，不少企業為了降低產品的采購價格，節省采購的運作費用，結成聯合采購合作戰略聯盟，例如，2015年7月，位于深圳寶能科技園的遠見總裁聯盟成員中的6家企業共同簽訂300萬元的原材料聯合采購協議.此外，還有一些第三方公司也搭建了聯合采購的平臺，匯集各方的需求，進行統一聯合采購，例如，2015年11月，中國房地產采購平臺“優采”的建立，實現了恒大地產、華遠地產等多家房地產企業針對“鋁合金電纜”的聯合采購②http：//news.dichan.sina.com.cn/2015/11/01/1132694.html.

雖然聯合采購受到了企業經理人的重視，但是，對此開展的研究還主要集中于采用實證與定性的方法，分析聯合采購活動將如何降低運作成本或增強企業的談判能力［1-4］，僅有較少的一些學者對此展開了理論上的分析.例如，MECA等在經典的EOQ和EPQ框架下對此問題進行了一系列的分析，他們在EOQ的框架下，考慮n個零售商協調訂貨周期，進行聯合采購的合作，分別建立了庫存成本博弈和持有成本博弈，并在此基礎上考慮了價格折扣對于聯合采購聯盟的影響［5-7］.此外，肖旦等則建立了制造商與零售商的庫存合作聯盟［8］；肖旦等在產品中含有次品情形下，探討了多個零售商從同一供應商處訂貨且進行統一檢測的聯合采購模型［9］.馮海榮等在不同聯合采購情形下討論了易腐品聯合采購費用的分攤問題［10-11］.

然而，在以上研究中，并沒有討論零售商產品合并運輸的情況.在實際運作中，為了節省費用，聯合采購的產品往往都是由供應商或者第三方物流公司統一配送的.例如，2011年，廣州地區的23所高校后勤部門以及餐飲中心負責人一起到廣州江南果菜批發市場，進行原材料的集中采購，并將采購到的產品統一配送至各高校①http：//news.cnwest.com/content/2011-03/17/content_4288350.htm.關于多個零售商進行聯合采購與合并運輸的合作模式，吸引了一些研究人員的關注.目前，FIESTRAS-JANEIRO等在經典的EOQ框架下，討論了多個零售商聯合運輸時的成本分攤問題［12］，曾銀蓮等分別討論了基于時間的合并運輸策略和基于數量的合并運輸策略下承運人運輸合作的費用分配問題，建立了相應的合作博弈模型，設計了屬于核的費用分配方案［13］.但是，他們并未考慮隨機需求環境下對零售商聯合采購與合并運輸聯盟訂貨決策和穩定性的影響.

本文在上述研究的基礎上，考慮隨機環境下零售商聯合采購與合并運輸聯盟的訂貨策略、成本分攤規則及其穩定性.得到了隨機環境下，零售商聯合采購與合并運輸聯盟的最優訂貨策略；隨后指出隨機環境下零售商聯合采購與合并運輸的合作戰略，并不一定能降低總的期望成本，由此給出了合作可以降低總期望成本的條件（即滿足次可加性的條件）；并在合作博弈滿足次可加性的條件下，根據邊際成本給出了可行的成本分攤規則，并證明了在此分攤規則下，可以保持大聯盟的穩定.

1 隨機環境下零售商聯合采購與合并運輸聯盟的訂貨量決策

本文在隨機需求環境下，考慮n個零售商進行聯合采購與基于時間策略的合并運輸戰略②時間策略的合并運輸是指基于時間進行訂單合并，即預設一個時間周期，每隔一個周期進行一次合并運輸.，其具體背景如下：①每一個零售商面臨的訂單是隨機到達的，令表示零售商i的第J筆訂單到達的時間，表示零售商i的第J筆訂單和第J+1筆訂單到達的間隔時間，即，可假設之間是相互獨立并且服從參數為λi的指數分布，因此，在（0，t）時間段內到達零售商i的訂單數量Ni（t）服從參數為λit的泊松分布，即E［ Ni（t）］＝λit.②假設零售商i的第J筆訂單的需求量相互獨立并且服從參數為μ的泊松分布，即E，則零售商i在（0，t）時間段內總的需求量為內，零售商們進行一次各種信息完全共享的聯合采購與合并運輸，供應商的補貨能力無限大，可隨時補貨并且及時到貨，其中，a表示每個零售商每次進行采購的啟動費用；c表示零售商采購單位產品的采購成本；Cdi表示從供應商到零售商i（i＝1，2，…n）的運輸成本，與供應商到零售商之間的距離成正比，設零售商均位于一條直線上，如果多個零售商形成聯合采購與運輸聯盟S，則聯盟S的運輸成本為聯盟中與供應商距離最遠零售商的運輸成本，即CdS＝max｛Cdi|i∈S｝.此外，hi表示零售商i（i＝1，2，…n）單位時間內單位產品的持有成本.由于泊松分布之和仍然是泊松分布，因此，對于任意的零售商集合SN，當他們進行聯合采購與合并運輸時，其總訂單到達率滿足參數為的泊松分布.

根據隨機過程中的更新理論可得出隨機環境下，零售商聯合采購與合并運輸聯盟單位時間內的總期望成本為

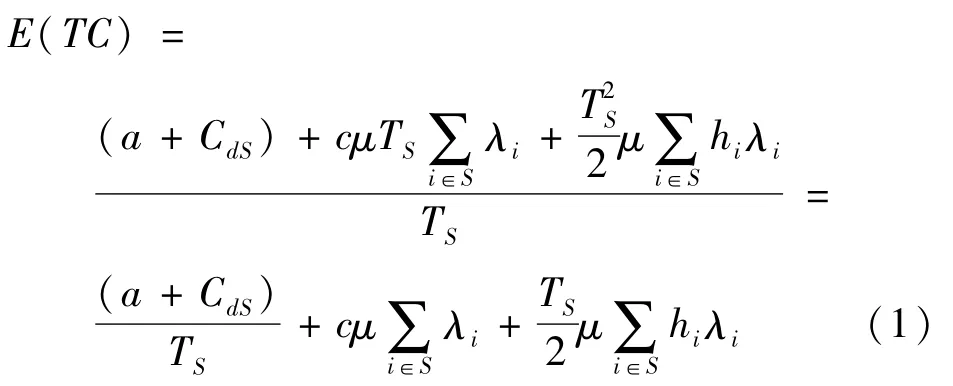
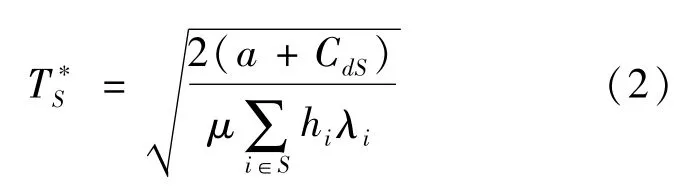
從而，隨機需求環境下，零售商聯合采購與合并運輸聯盟單位時間的最小總期望成本為

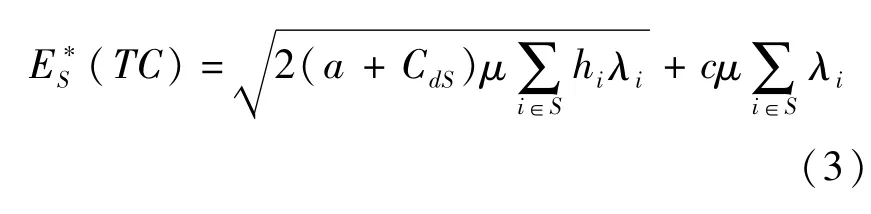
2 隨機環境下零售商聯合采購與合并運輸聯盟的次可加性

隨機環境下，零售商之間會形成不同的聯合采購與合并運輸聯盟，它們將產生不同的運作成本，聯盟的成本可以用特征函數c（S）刻畫，定義為：一個給定的隨機環境下零售商聯合采購與合并運輸的合作博弈模型為（N，c），其中N表示零售商的集合，c為合作聯盟的成本.

下面的定理1將說明在一般情形下，合作博弈（N，c）并不滿足次可加性，這與曾銀蓮等［13］在隨機需求環境下零擔貨物運輸合作研究中所得到的結論是不同的.這是因為，在文獻［13］中曾銀蓮等討論的基于時間策略下的合作運輸博弈問題，僅僅考慮了多個零售商將訂單通過統一訂貨周期合并在一起采購產品的情形，并沒有考慮產品運輸到零售商處的運輸成本對于聯盟的影響.然而，在實際中不少零售商不僅進行聯合采購，而且還進行合并運輸，此外，產品送至每個零售商處的運輸成本存在差別.因此，本文考慮到運輸成本對于零售商結盟的影響，例如，當2個零售商合作時，如果一個零售商的運輸成本較高，而另一個零售商的運輸成本較低，他們形成聯合采購與合并運輸聯盟所采用的最優訂貨周期，將可能會使某一個零售商在一個訂貨周期內的訂貨量較多，從而使系統產生比分開時還高的成本，即不滿足次可加性.

即c（S∪T）≤c（S）+c（T）等價于

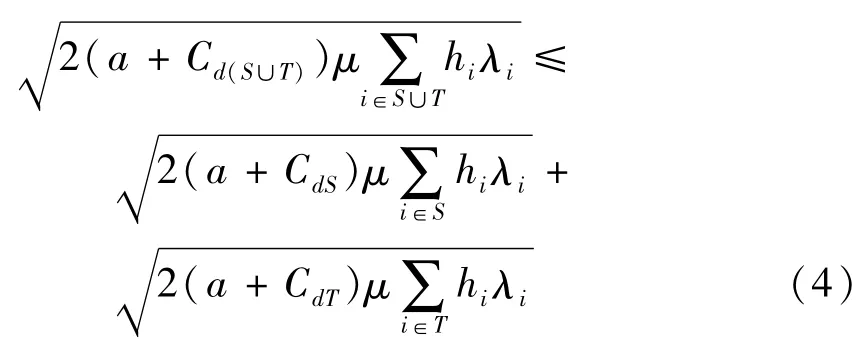
將式（4）兩邊同時平方后考慮如下2個式子，

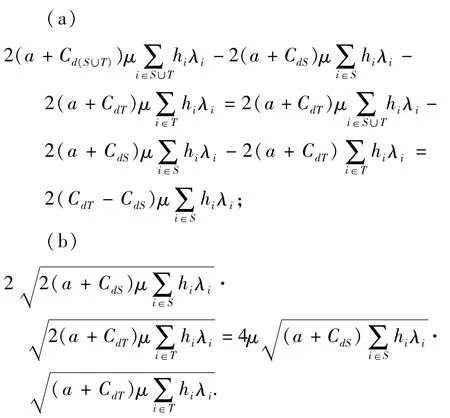
3 隨機環境下零售商聯合采購與合并運輸聯盟的穩定性

定義2 滿足如下條件的集合稱為合作博弈（N，c）的核：

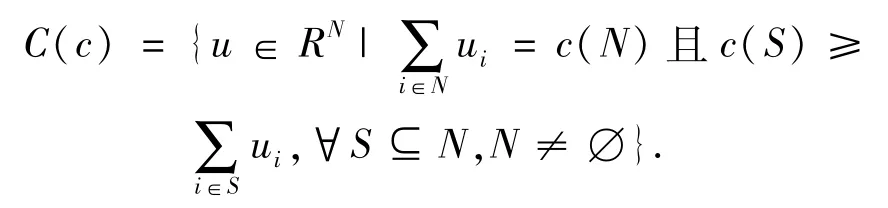
定義5 令π（N）是N的所有置換σ：N→N的集合，集合Pσ（i）：＝｛r∈N|σ-1（r）＜σ-1（i）｝含有關于置換σ的所有i的前繼.

關于置換σ和合作博弈（N，v）的邊際貢獻向量mσ（N，v）∈Rn，定義為對所有i∈N，mσ（N，v）的第i個分量為

隨機環境下，如果零售商聯合采購與合并運輸合作博弈（N，c）滿足次可加性，則將零售商按照其與供應商之間的距離由遠及近降序排列的全體記為π（N，A），從而，聯合采購與合并運輸大聯盟N的運作成本可按如下的規則進行分攤：

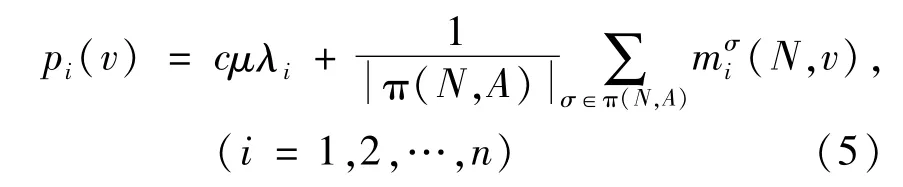
定理2 成本分攤規則p（v）＝（p1（v），p2（v），…，pn（v））是隨機環境下零售商聯合采購與合并運輸合作博弈的一個核配置.

證明

（1）對于

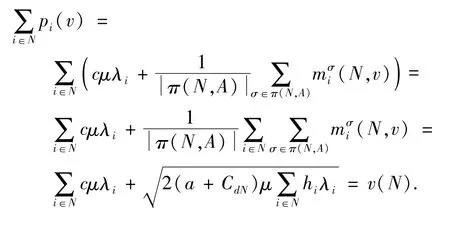
（2）a.如果聯合運輸與采購聯盟S中含有距供應商最遠的零售商σ-1（1），則有，

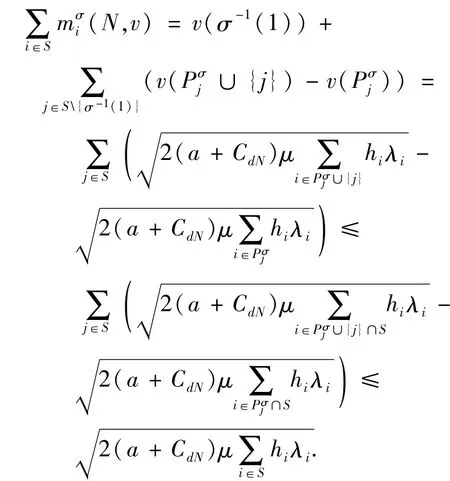
b.如果聯合采購與運輸聯盟S中不包含距供應商最遠的零售商σ-1（1）.則令（1）｝，可知，由合作博弈（N，v）的次可加性，有成立.因此，），從而則有也成立.

4 數值例子

本小節將通過一個實際案例，對本文所提出的成本分攤規則進行說明.假設所考慮的隨機需求環境下聯合采購與合并運輸供應鏈中僅有3個零售商，分別為“全家”在廣州大學城的3個超市，分別編號為1，2，3，據調研可知，他們每天會聯合采購“怡寶”礦泉水并進行合并運輸.設每家“全家”超市每天內的單數量為λi（i＝1，2，3），每一筆訂單的平均需求量為μ，配送中心到超市的運輸成本為Cdi（i＝1，2，3），而每一家超市的持有成本為hi（i＝1，2，3），統一的進貨成本為c，3家超市的具體參數見表1.

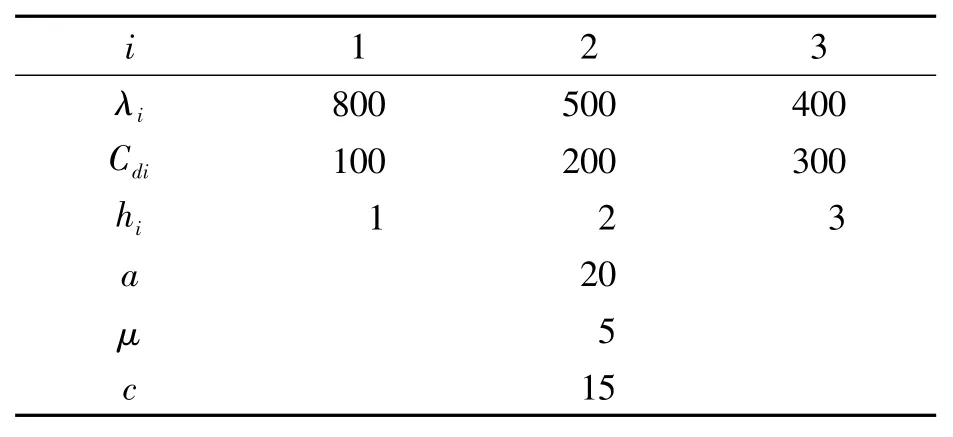
表1 3個零售商的參數Table 1 Parameters of three retailers

通過表2可知，在表1所給出的參數下，隨機需求環境下零售商聯合采購與合并運輸合作博弈滿足次可加性，從而零售商之間進行合作是可以獲益的.因此，表3則給出了零售商間形成不同合作聯盟時的運作成本.

表2 聯合采購與合并運輸合作博弈的次可加性Table 2 Subadditivity of collaborative procurement and shipment consolidation game

表3 聯合采購與合并運輸聯盟的運作成本Table 3 Operational cost of collaborative procurement and shipment consolidation coalitions

由系統給定的參數可知，π（N，A）＝｛（3，2，1）｝，根據pi（v）的計算公式可知，按分配規則p（v）所給出的成本分攤方案為：（60 898.4，37 740.4，31 959.6），該分配方案在聯合采購與合并運輸合作博弈的核中.

5 結 論

文章建立了隨機需求環境下，零售商聯合采購與合并運輸聯盟的合作博弈模型.首先，在隨機到達的需求下得到了零售商進行聯合采購與合并運輸聯盟的最優訂貨策略；隨后，指出在隨機環境下零售商的聯合采購與合并運輸戰略并不一定能降低各自的成本，并給出了合作可以降低各自成本的條件（即滿足次可加性的條件）；根據邊際成本給出了可行的成本分攤規則，并證明了在此分攤規則下，可以保持大聯盟的穩定，最后通過一個具體的實例對成本分攤方案進行了說明.

［1］ ESSIG M.Purchasing consortia as symbiotic relationships：Developing the concept of“consortium sourcing”［J］.Eur J Purch Supply Manag，2000，6（1）：13-22.

［2］ TELLA E，VIROLAINEN V M.Motives behind purchasing consortia［J］.Int J Prod Econ，2005，93：161-168.

［3］ HEIJBOER G.Mathematical and statistical analysis of initial purchasing decisions［D］.Enschede：University of Twente，2003.

［4］ DANA J.Buyer groups as strategic commitments［R］.Evanston：Kellogg School of Business Working Paper，Northwestern University，2004.

［5］ MECA A，TIMMER J，GARCíA-JURADO I，et al.Inventory games［J］.Eur J Oper Res，2004：127-139.

［6］ MECA A，GARCíA-JURADO I，BORM P.Cooperation and competition in inventory games［J］.Math Meth Oper Res，2003，57（3）：481-493.

［7］ MECA A，GUARDIOLA L A，TOLEDO A.P-Additive games：A class of totally balanced games arising from inventory situations with temporary discounts［J］.TOP，2007，15：322-340.

［8］ 肖旦，周永務.數量折扣契約下制造商與零售商庫存合作聯盟的穩定性［J］.運籌與管理，2013，22（2）：20-26，43.XIAO D，ZHOU Y W.Stability of the inventory coalitions of manufacturer and retailers under quantity discount contract［J］.Oper Res Manag Sci，2013，22（2）：20-26，43.

［9］ 肖旦，周永務，湯勤深.考慮次品率的零售商庫存聯盟訂貨量與穩定性分析［J］.工業工程，2013，16（3）：32-37.XIAO D，ZHOU Y W，TANG Q S.On stability of retailers′coalition for items with imperfect quality［J］.Ind Eng J，2013，16（3）：32-37.

［10］馮海榮，李軍，曾銀蓮.易腐品供應鏈企業聯合采購決策與費用分配研究［J］.系統科學與數學，2011，31（11）：1454-1466.FENG H R，LI J，ZENG Y L.Study on collaborative purchasing and cost allocation problem in supply chains with perishable products［J］.J Syst Sci Math Sci，2011，31（11）：1454-1466.

［11］馮海榮，李軍，曾銀蓮.延期支付下的易腐品聯合采購費用分配［J］.系統工程理論與實踐，2013，33（6）：1411-1423.FENG H R，LI J，ZENG Y L.Cost allocation for collaborative procurement on perishable products under permissible delay in payments［J］.Syst Eng Theory Pract，2013，33（6）：1411-1423.

［12］FIESTRAS-JANEIRO M，GARCíA-JURADO I，MECA A，et al.Cost allocation in inventory transportation systems［J］.TOP，2012，20（2）：397-410.

［13］曾銀蓮，李軍，馮海榮.隨機需求環境下零擔貨物運輸合作［J］.管理科學學報，2015，18（7）：48-58.ZENG Y L，L J，FENG H R.Collaboration in less-than-truckload transportation with stochastic demand［J］.J Manag Sci China，2015，18（7）：48-58.

Stability of retailers’coalition w ith collaborative procurement and shipment consolidation under stochastic demand

XIAO Dan，LIU Fang，SHI Xin-xiang，Q IN Long-yi
（School of Business Administration，Guangzhou University，Guangzhou 510006，China）

In order to reduce operating cost，companies will form coalitions which adopt strategies of collaborative procurement and shipment consolidation under stochastic demand.However，they have to allocate the operational cost fairly and rationally to keep the stability of coalition.This paper uses cooperative game to analyze the stability of retailers'coalition with collaborative procurement and shipment consolidation under stochastic demand.First of all，we get the optimal order quantities of the coalition.Then，we show that the cooperation of purchasement and shipment will not always reduce the total operating costs，we give the conditions under which the cooperation will be better for all members.Lastly，we provide that a cost allocation rule for the case that follows from each retailer's marginal cost will keep the grand coalition stability.

stochastic demand；shipment consolidation；order quantity；stability

F 275

A

1671-4229（2016）01-0090-06

【責任編輯：孫向榮】

2015-11-02；

2015-12-02

廣東省自然科學基金博士啟動資助項目（2014A030310443，2015A030310192）；教育部人文社科項目一般資助項目（15YJC630138，15YJC630072）

肖旦（1986-），男，講師.E-mail：danx2003＠hotmail.com.