基于復制測量法的球頭立銑刀磨損預測研究

孫 博，陳錦江，王 芳，孫占偉，田廣偉

(燕山大學 機械工程學院，秦皇島 河北 066004)

?

基于復制測量法的球頭立銑刀磨損預測研究

孫 博，陳錦江，王 芳，孫占偉，田廣偉

(燕山大學 機械工程學院，秦皇島 河北 066004)

論文提出一種測量球頭立銑刀磨損量的復制測量方法并分析該方法的誤差。以銑刀徑向磨損量為研究對象進行刀具磨損試驗，找出銑削參數對刀具磨損的影響規律，得出徑向磨損量增量與銑削參數的銑刀磨損模型和刀具壽命經驗公式，并通過試驗驗證磨損模型具有較高精度，可用于磨損量預測。

球頭立銑刀；徑向磨損量；復制測量；磨損試驗

0 引言

高速銑削技術在近幾年得到快速發展[1]，但其刀具工作條件要比普通銑削復雜，刀具磨損尤顯突出。在高速銑削3Cr2Mo模具鋼的過程中，由于沒有定量描述刀具磨損的方法和缺乏對刀具磨損規律深入的認識，刀具性能未能充分發揮；依據傳統方法無法確定合理的高速銑削參數，而依據加工經驗確定的銑削參數又不能發揮高速銑削技術的優勢。傳統的測量刀具磨損方法已無法滿足需求[2]。

針對刀具磨損建模，常艷麗[3]通過試驗得出刀具切削鎳基高溫合金(GH4169)的主要磨損機理為粘結磨損，進而選擇Archard磨損模型進行力、熱等試驗確定模型系數，建立了刀具磨損理論模型。K. Venkata Rao等[4]通過人工神經網絡算法預測以AISI 316為工件刀具磨損和粗糙度，經試驗驗證預測值具有較高準確性。

本文提出一種測量球頭立銑刀磨損量的復制測量方法，實現了刀具磨損試驗過程的連續性和測量磨損量的準確性；同時以徑向磨損量為研究對象進行刀具磨損試驗，建立包含刀具徑向磨損增量與銑削參數的磨損模型，以研究銑削參數對刀具磨損量和刀具壽命的影響規律，為生產實際提供一定依據。

1 球頭立銑刀磨損量的復制測量

1.1 測量方法

目前測量立銑刀磨損量常用萬能工具顯微鏡測量刀具幾何參數進而確定刀具磨損量，其測量過程繁瑣，測量時間長[5]。本文借鑒“銑削刀具輪廓復制”[6]的思想提出“復制測量”方法，使磨損量的測量過程從試驗過程中分離，以實現刀具磨損試驗過程的連續并縮短試驗用時。

圖1 球頭立銑刀銑削微元

復制測量方法是以“復制孔輪廓圓的半徑代替球頭立銑刀的徑向半徑”為特征，通過“圖像法測量輪廓圓半徑”進而得到刀具徑向磨損量的方法。

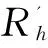
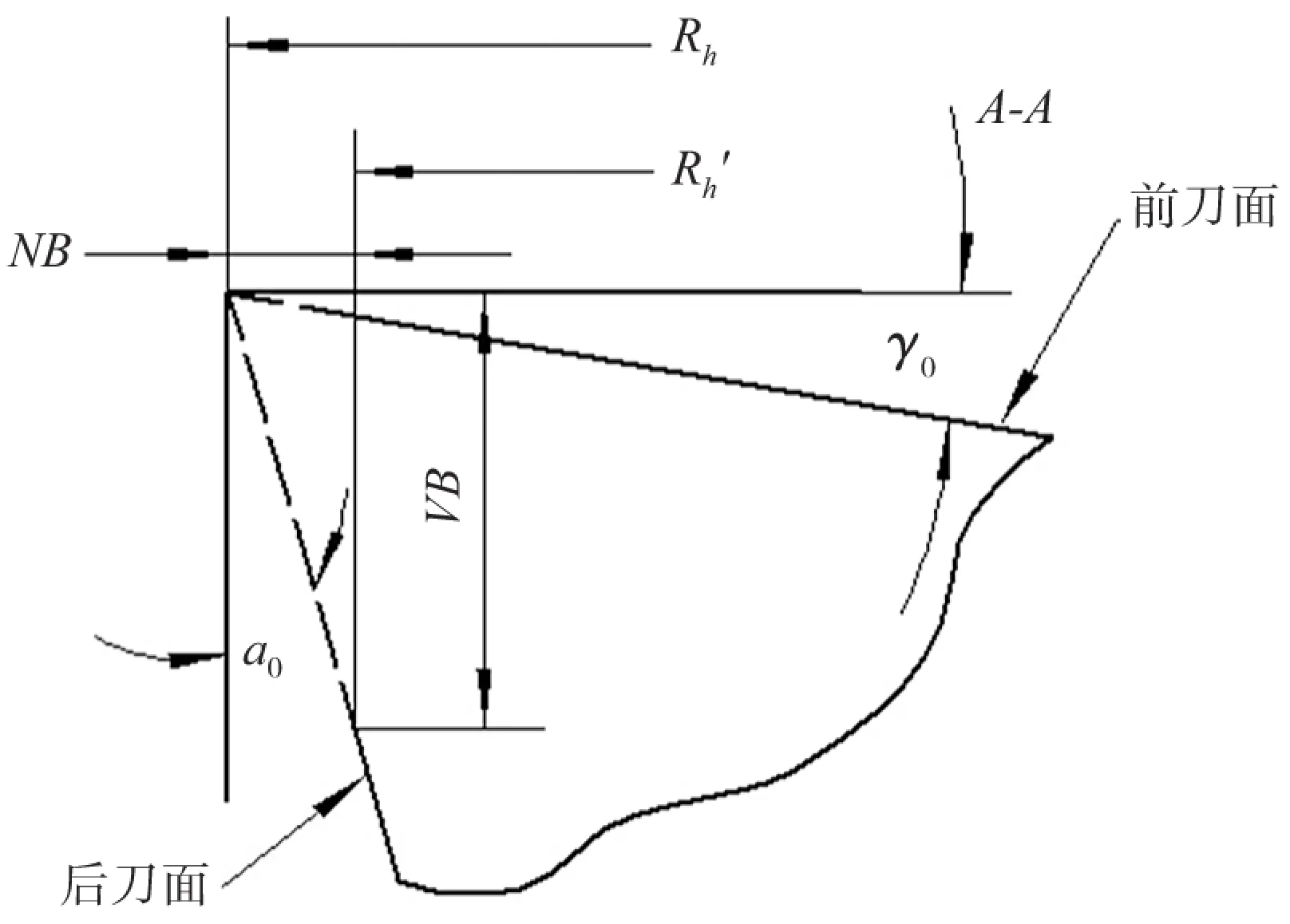
圖2 VB與NB關系示意圖

由式(1)知VB與NB存在線性關系，而立銑刀壽命試驗的國標中推薦VB作為判別刀具是否失效的判據，故NB可替代VB，亦即徑向磨損量可以衡量刀具的磨損程度。

銑刀h處截面微圓半徑Rh的復制方法為：用半徑為R的球頭立銑刀在平板(稱復制板)上銑削出深度為h的孔(稱復制孔)，復制孔深度h依據1/2銑削深度處的切削刃位置確定，如圖3所示。把孔在復制板上表面輪廓圓的半徑值Rh作為刀具相應部分截面半徑值R。

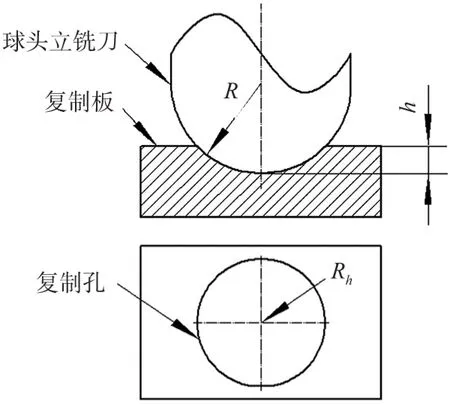
圖3 刀具徑向半徑測量圖

通過圖像法測量復制孔輪廓圓半徑Rh的方法是用OLYMPUS OLS3100型激光共焦顯微鏡對復制孔拍照，獲得孔輪廓圓圖像，如圖4所示，再通過軟件MATLAB提供的edge函數實現輪廓圓邊緣的Canny算子檢測[7]。如圖5所示，在圓周邊緣取近似均分的12個標記點。由最小二乘原理，求擬合圓的半徑相當于求解以下問題：

(2)

式(2)為3參數、線性約束的優化問題，從而可求得半徑Rh值。

圖4 拍攝的輪廓圓圖像 圖5 帶標記點坐標輪廓圓圖像

每次銑削試驗開始和結束時分別在復制板上銑削出同樣深度的兩孔，兩個復制孔輪廓圓半徑值Rh的差即為試驗過程中刀具的徑向磨損量。

1.2 復制測量方法的誤差分析

一般地，刀具徑向半徑等于復制孔輪廓圓半徑等于復制孔輪廓圓半徑的測量值。然而由于存在誤差，需要確定每次試驗時，每個復制孔的測量次數和銑削幾個復制孔。

(1)測量次數誤差分析

用圖像法對同一個復制孔測量9次[8]輪廓圓半徑得其測量值見表1。

對測量數據進行正態性檢驗，如圖6所示。P值為使用Anderson-Darling統計量

檢驗數據是否服從指定分布的判定值，當P值大于0.05時，認為數據不服從指定分布。計算可得P值為0.694，因此數據符合正態分布。

圖像法測量半徑值的誤差(取標準差)為0.6μm，期望圖像法測量半徑的誤差不大于1μm，故圖像法1次測量半徑值已滿足精度要求。

表1 輪廓圓半徑測量值

表2 復制孔輪廓圓半徑的測量值

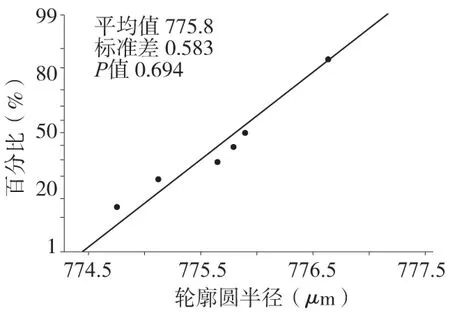
圖6 圖像法正態性檢驗

圖7 復制測量正態性檢驗

(2)復制測量誤差分析

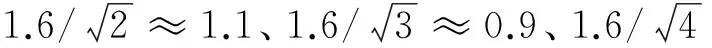
2 刀具磨損試驗與建模

2.1 試驗條件

機床為DMU 60 monoBLOCK數控加工中心。刀具為OSK系列整體式硬質合金球頭立銑刀，型號KM 2BRNL，規格R1.5×2.4×N12×70×6。工件材料為3Cr2Mo，預硬處理，尺寸為190×60×25mm。復制板材料與工件的相同，上下面精磨且上表面拋光處理，圖8為安裝在工作臺上的工件和復制板。銑削方式為往復式等距走刀銑削平面，使用乳化液。刀具傾角β為15°[9]。

圖8 安裝在工作臺上的工件和復制板

2.2 試驗方案與記錄

根據試驗參數的范圍選定各因素水平，如表3所示。

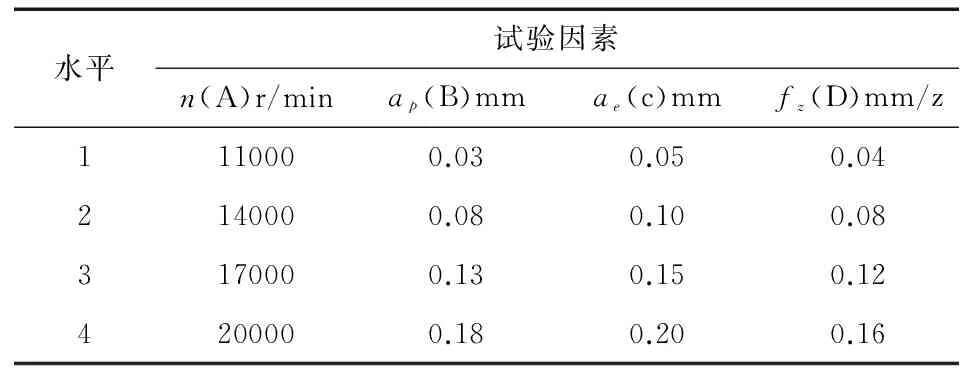
表3 正交試驗因素水平表

注：表中n為主軸轉速，ap為銑削深度，ae為銑削寬度，fz為每齒進給量，下同。

銑削深度為0.03、0.08、0.13和0.18mm時對應復制孔的深度分別是0.12、0.18、0.23和0.27mm。每次試驗銑削3個復制孔，其切削用量與加工時的相同；主軸轉速2000r/min，每齒進給量0.005mm/z。試驗全部完成后卸下復制板，用復制測量方法測量復制孔輪廓圓半徑，如表4所示。

表中ΔNB為每次試驗對應的刀具磨損量增量，第Ⅰ、Ⅱ、Ⅲ、Ⅳ行為銑削試驗之前復制孔的徑向半徑，此時刀具磨損為零。

設球頭立銑刀某截面初始半徑為Rh，切削時刻為t1時半徑變為Rh1,繼續加工至t2時半徑變為Rh2，則t2時間內對應刀具磨損量增量ΔNB是：

ΔNB=NB2-NB1=(Rh-Rh2)-(Rh-Rh1)=Rh1-Rh2

(3)

2.3 試驗結果分析

隨著切削時間t的增加，刀具磨損量會逐漸增加。刀具到達急劇磨損階段之前，磨損量的變化率近乎為定值[10]，即：

ΔVB/Δt=K

(4)

式中K——刀具磨損率，與工況相關系數。

由式(1)可知VB和NB存在線性關系，故：

ΔNB/Δt=K＇

(5)

即刀具徑向磨損量增量與銑削時間呈線性關系。考慮實際銑削過程復雜性將線性關系修正為指數關系,即

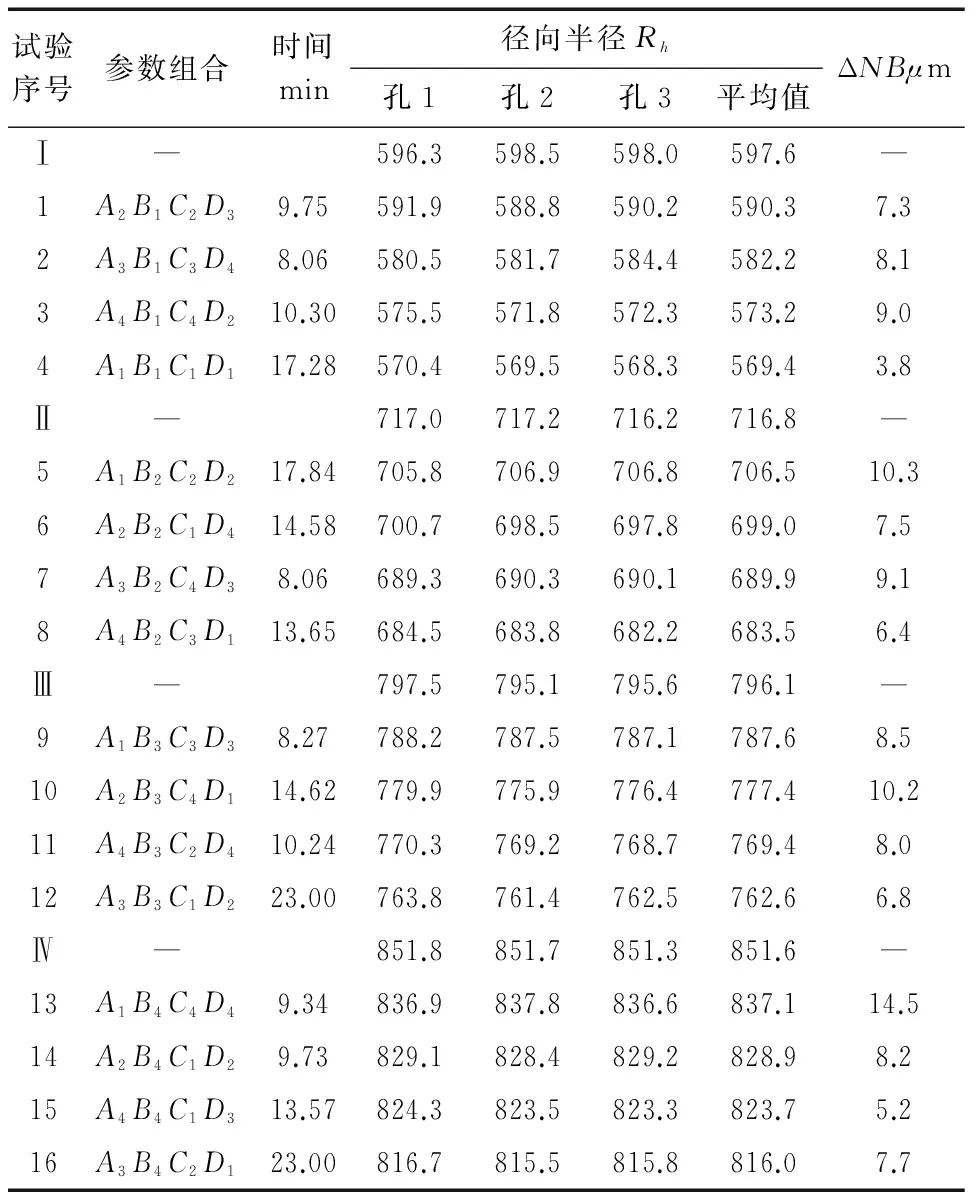
ΔNB= K＇Δtλ (6)

式(7)可改寫為：

(8)

式中C——與刀具、材料、銑削方式等相關的工況系數；

α——主軸轉速系數；

β——銑削深度系數；

γ——銑削寬度系數；

δ——每齒進給量系數。

對式(8)兩邊取對數，得

lgΔNB=lgc+αlgn+βlgap+γlgae+λlgΔt

(9)

由式(9)可知刀具徑向磨損量與銑削參數之間存在線性關系，故使用回歸分析中的多元線性回歸法來建立刀具磨損模型:

(10)

為判斷各參數對刀具徑向磨損量是否顯著，需對回歸模型進行統計假設檢驗，結果見表5和表6。

由此可知：銑削參數按對磨損的影響程度由大到小為：銑削寬度，每齒進給量，主軸轉速和銑削深度。

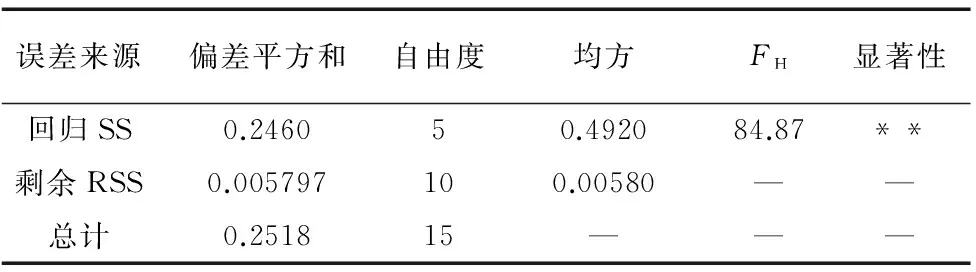
表5 方程顯著性檢驗的方差分析表

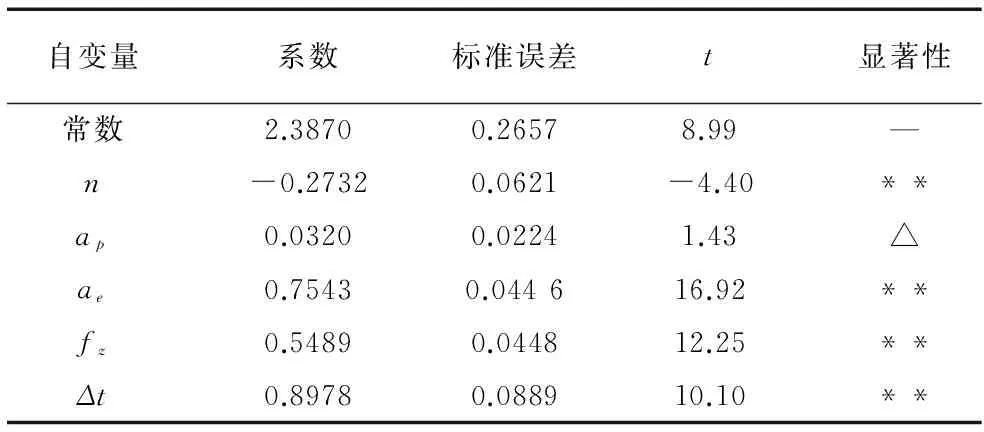
表6 回歸系數顯著性檢驗的方差分析表

注：**表示因素在α水平取0.01時顯著，△表示α水平介于0.2～0.1時顯著。

2.4 銑削參數對刀具壽命的影響

以刀具壽命為考察對象的刀具磨損試驗，是通過徑向磨損量增量與銑削參數的模型來獲得刀具壽命經驗公式。取刀具磨鈍標準為徑向磨損量NBT=60μm，帶入式(10)后，整理得：

(11)

由式(11)可知，提高主軸轉速時，會增加刀具壽命；隨著銑削深度、銑削寬度和每齒進給量的增加，刀具壽命有減小的趨勢。從提高刀具壽命的角度考慮，高速銑削3Cr2Mo模具鋼時，建議采用較高的主軸轉速，較小的銑削深度、銑削寬度和每齒進給量。

2.5 磨損模型的驗證

刀具磨損模型既可用于預測磨損量，也可用于以減小磨損率為目標的銑削參數優化。銑削過程中，由于立銑刀的不斷磨損,使切削刃實際加工位置與設計位置出現偏移從而產生加工誤差；在高精度加工中，刀具磨損模型可用于根據刀具的磨損量對加工誤差進行補償。按表7中試驗參數進行銑削試驗。

表7 驗證試驗用銑削參數表

試驗完成后用復制測量的方法得到磨損量的實測值ΔNB1，求出磨損量預測值ΔNB2，對比兩者見表8。相對誤差為-15.9%～6.1%，說明該回歸模型有較高的預測精度可用于磨損量預測。

表8 磨損量增量實測值與預測值對比

3 結束語

本文提出復制測量方法測量球頭立銑刀磨損量，通過銑削試驗的數據得到了φ3球頭立銑刀徑向磨損增量與銑削參數及銑削時間的模型，研究了銑削參數對刀具壽命的影響，得到以下結論：

(1)主軸轉速、銑削寬度、每齒進給量對刀具徑向磨損影響較大，銑削深度對磨損影響較小。

(2)刀具壽命隨主軸轉速的提高而增加，隨銑削深度、銑削寬度和每齒進給量的增加而減小。從提高刀具壽命角度考慮，可采用高的主軸轉速，較小的銑削深度、銑削寬度和每齒進給量加工3Cr2Mo模具鋼。

(3)所建刀具磨損模型有較高的精度，可用于刀具磨損量的預測。

[1] 何寧. 高速切削技術[M]. 上海: 上海科學技術出版社, 2012.

[2] 禹杰,林有希,林華. 高速銑削刀具磨損研究進展[J]. 工具技術, 2015(9): 3-6.

[3] 常艷麗. 鎳基高溫合金GH4169的切削力與刀具磨損試驗研究[D]. 哈爾濱: 哈爾濱工業大學, 2011.

[4] K Venkata Rao a, B S N Murthy, N Mohan Rao. Prediction of cutting tool wear, surface roughness and vibration of work piece in boring of AISI 316 steel with artificial neural network [J]. Measurement, 2014,51: 63-70.

[5] 梁偉云, 郭井寬, 陳曉波, 等. 基于影像視覺的立銑刀磨損狀態檢測技術研究與系統開發[J]. 工具技術, 2012(12): 59-64.

[6] 張臣. 數控銑削加工物理仿真關鍵技術研究[D]. 南京:南京航空航天大學, 2006.

[7] 林周品, 李曉東. MATLAB數字圖像處理[M]. 北京: 清華大學出版社, 2012.

[8] 費業泰. 誤差理論與數據處理[M]. 北京: 機械工業出版社, 2015.

[9] Ko T J, Kim H S, Lee S S. Selection of the Machining Inclination Angle in High-Speed Ball End Milling[J]. Int J Adv Manuf Technol, 2001,17 (3): 163-170.

[10] GB/T 16461—1996. 單刃車削刀具壽命試驗[S].北京：中國標準出版社，1996.

(編輯 李秀敏)

Study on Prediction of Ball End Mill Wear Based on Copy Measurement

SUN Bo,CHEN Jin-jiang,WANG Fang,SUN Zhan-wei,TIAN Guang-wei

(College of Mechanical Engineering Yanshan University, Qinhuangdao Hebei 066004,China)

This paper proposes a copy measurement of ball end mill wear and analyzes the error of this method. The radial mill wear quantity as the research object for the tool wear test, find out the influence law of milling parameters on tool wear. It is concluded that the radial wear increment and the milling parameters of milling cutter tool wear model and tool life experience formula can be obtained, and through the test the wear model has higher accuracy and is useful to predict the amount of wear.

ball end mill ; radial wear; copy measurement; tool wear test

1001-2265(2016)09-0000-00

10.13462/j.cnki.mmtamt.2016.09.000

2015-11-03；

2015-12-07

孫博(1990—)，男，吉林農安人，燕山大學碩士研究生，研究方向為切削加工，(E-mail)sunboysu@163.com。

TH161;TG501.3

A