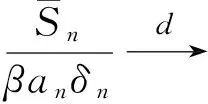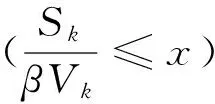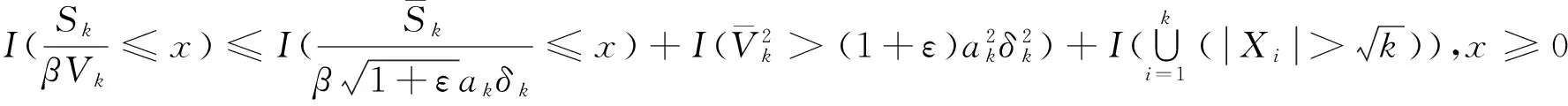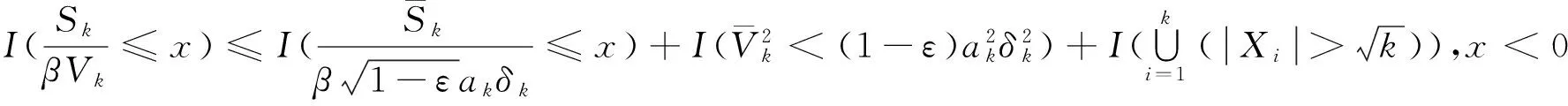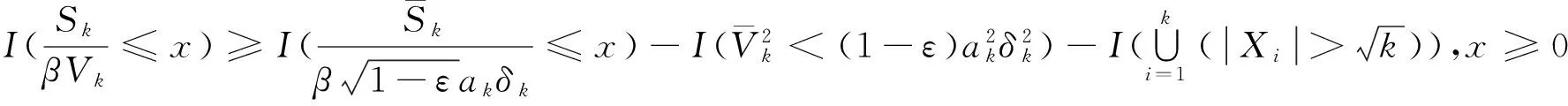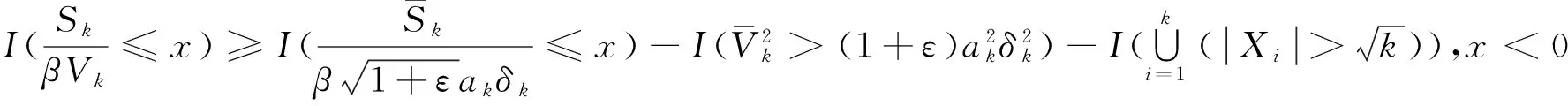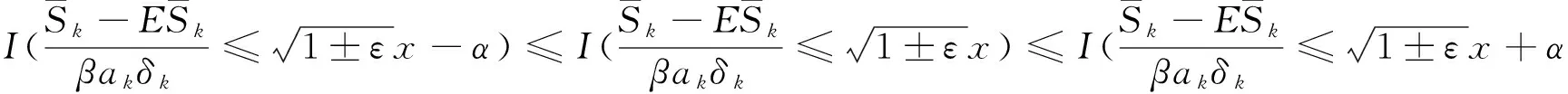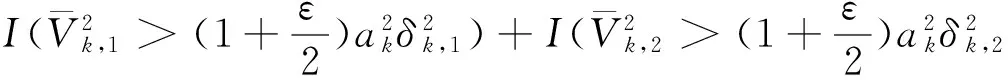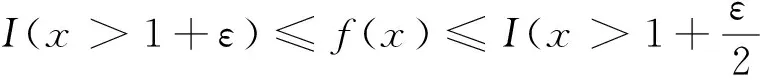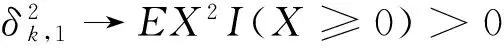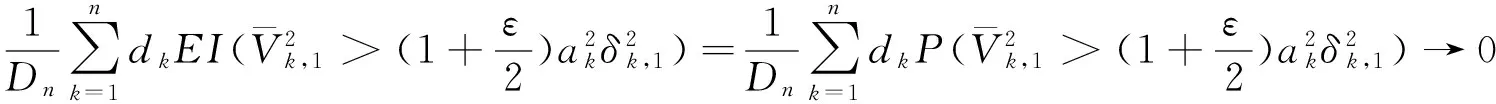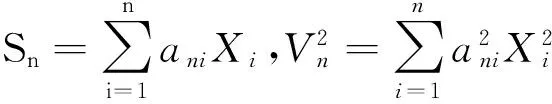NA序列自正則加權和的幾乎處處中心極限定理
付宗魁,吳群英
(桂林理工大學理學院,中國 桂林 541004)
?
NA序列自正則加權和的幾乎處處中心極限定理
付宗魁*,吳群英
(桂林理工大學理學院,中國 桂林 541004)
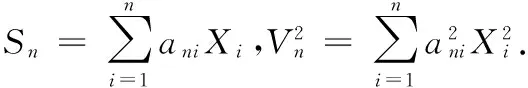
NA序列; 自正則加權和; 幾乎處處中心極限定理
稱隨機變量X1,X2,…,Xn,n≥2是Negatively Associated (簡記為NA)的,若對集合{1,2,…,n}的任意兩個非空不交子集A1,A2,均有cov(f1(Xi;i∈A1),f2(Xj;j∈A2))≤0.其中,fi,i=1,2是使上式有意義且對各變元不降(或不升)的函數.稱隨機變量序列{Xn,n≥1}是NA列,如果對任意n≥2,X1,X2,…,Xn是NA的.近年來,自正則極限理論是概率論研究的一個熱門話題,許多學者已得到了很多結果.文獻[1]得到了混合序列自正則隨機和乘積的漸近性;文獻[2]得到了自正則和在正態吸引律下的幾乎處處中心極限定理,文獻[3]得到了φ混合序列自正則加權和的中心極限定理等.但關于自正則加權和的極限理論研究不多,本文討論了NA序列自正則加權和的幾乎處處中心極限定理.
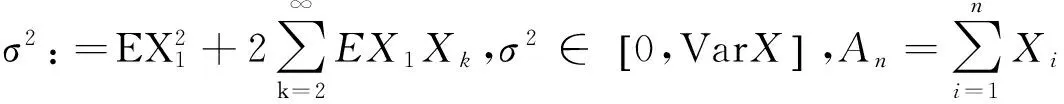
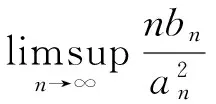
(1)
定理1 設{X,Xn,n≥1}是均值為零的嚴平穩NA序列,EX2<∞,對任意的常數β>0,則有
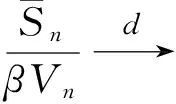
(2)
其中,N為標準正態隨機變量.
定理2 設{X,Xn,n≥1}是均值為零的嚴平穩NA序列,{ani,1≤i≤n,n≥1}為實數陣列且滿足式(1),并且
(3)
對于任意的β>0,使得
(4)
(5)
則有
(6)
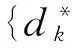
注2 如果{X,Xn,n≥1}為獨立同分布的隨機變量序列,則式(4)中β=1.
1 基本引理
引理1[5]設{Xn,n≥1}為NA隨機變量序列,如果{fi,i∈N}是一列非降(或非升)的函數,則{fi(Xi),i∈N}仍是NA的.
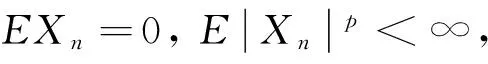
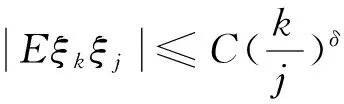
證 由EX2<∞,則有
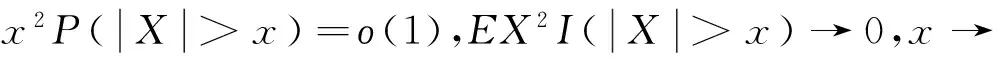
(7)
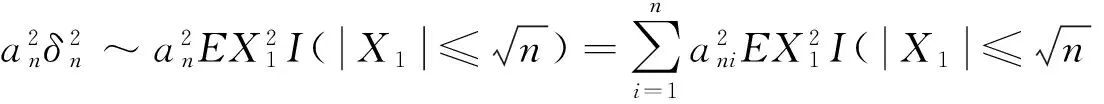
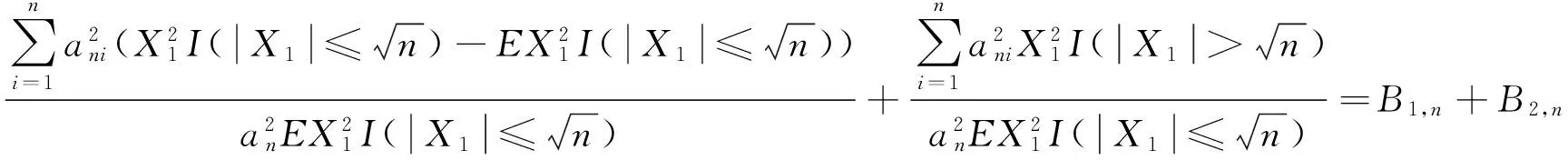
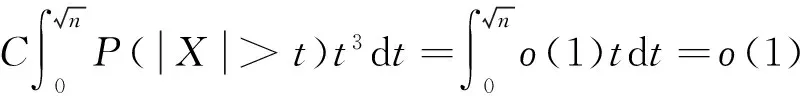
(8)
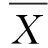
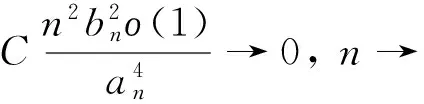
(9)
由式(1)和(7),則有
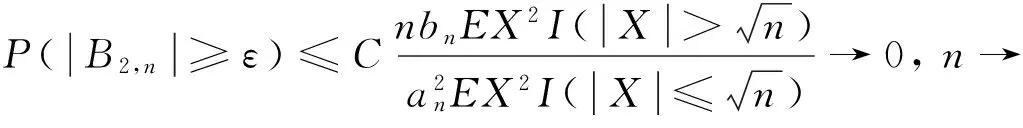
(10)
引理5 在定理2的條件下,dk和Dn滿足式(5),如果f(x)為有界且具有連續導數的函數,則有
(11)
(12)
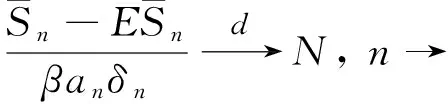
(13)
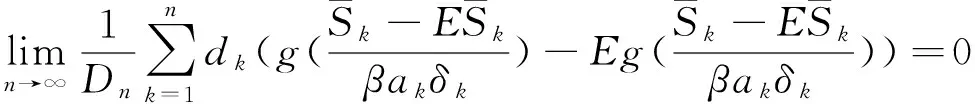
(14)
對任意的1≤k 由文獻[8]的引理3知,當EX2<∞和σ2>0時,則有 (15) 由式(1)和(15),則有 因此,式(14)成立,由引理3知式(11)成立. 由引理3知式(12)成立. 定理1的證明 為了證明式(2),由引理4,則只需證 (16) (17) 定理2的證明 對任意的0<ε<1,則有 因此, 類似地,有 為了證明式(6),只需要證明 (18) (19) (20) 對任意所為ε>0,為了證明式(19),則只需證 (22) 設f(x)為有界且具有連續導數的函數,對任意的ε>0,則有 (23) 由式(23),(12)及Toeplitz引理,則有 當l=2時,式(22)也成立.于是,式(19)成立.類似式(19)的證明知式(20)也成立.類似文獻[9]中式(2.33)的證明知式(21)成立. [1] LIU W D,Lin Z Y.Asymptotics for self-normalized random products of sums for mixing sequences[J].Stoch Anal Appl,2007,25(2):293-315. [2] WU Q Y.A note on the almost sure limit theorem for self-normalized partial sums of random variables in the domain of attraction of the normal law[J].Inequal Appl,2012,17(1):242-252. [3] 劉 影,張 勇,董志山.φ混合序列自正則加權和的中心極限定理[J].吉林大學學報(自然科學版),2008,46(3):643-648. [4] NEWMAN C M.Normal fluctuations and the FKG inequalities[J].Comm Math Phys,1980,74(2):119-128. [5] 群 英.混合序列的概率極限理論[M].北京:科學出版社,2006. [6] BILLINGSLEY P.Convergence of probability measures[M].New York: Wiley,1968. [7] PELIGRAD M,SHAO Q M.A note on the almost sure central limit theorem for weakly dependent random variables[J].Statist Probab Lett,1995,22(2):131-136. [8] ZHANG L X.The weak convergence for functions of negatively associated random variables[J].Multivar Anal,2001,78(6):272-298. [9] WU Q Y.Almost sure central limit theory for self-normalized products of sums of partial sums[J].J Math Anal Appl,2012,27(2):243-257. (編輯 HWJ) Almost Sure Central Limit Theorem for Self-Normalized Weighted Sums of Negatively Associated Random Variables FU Zong-kui*,WU Qun-ying (College of Science,Guilin University of Technology,Guilin 541004,China) negatively associated random variables; self-normalized weighted sums; almost sure central limit theorem 10.7612/j.issn.1000-2537.2016.05.016 2015-10-10 國家自然科學基金( 11361019);廣西自然科學基金重點項目 (2013GXNSFDA019001);廣西高校人才小高地建設創新團隊資助計劃(桂教人[2011]47號) *通訊作者,E-mail:gut_fuzongkui@163.com O211.4 A 1000-2537(2016)05-0089-06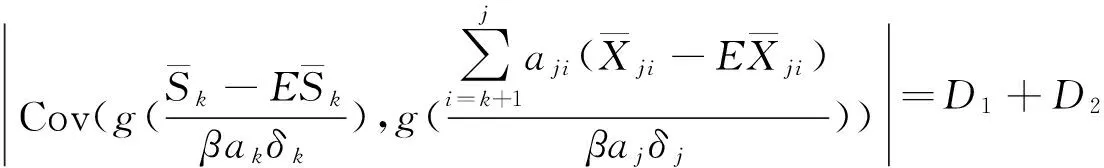
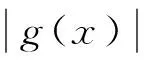
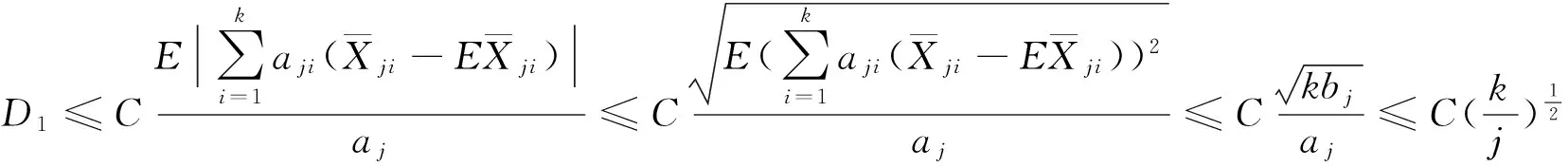
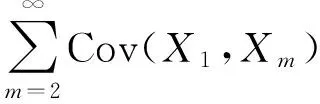
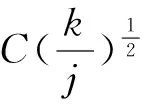
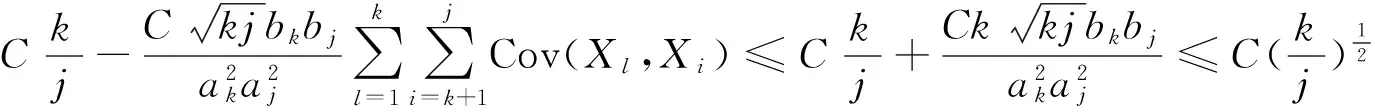
2 定理的證明