運用比較法讓初中數學課化繁為簡
王文娟
河北省冀州市冀州鎮中學
?
運用比較法讓初中數學課化繁為簡
王文娟
河北省冀州市冀州鎮中學
數學問題浩如煙海,面對一個個數學問題如何著手求解?有些學生做了大量的題目,但考試遇到新題型或只是稍稍變換一下,就不知所措,原因是在平時的學習中,缺乏掌握數學思考方法。掌握一種新的思考方法要比學會解幾道具體習題更為重要,這些解題方法和技巧是進一步學習數學不可缺少的工具,數學方法的學習,在數學學習中起到事半功倍的效果。比較法就是找出一事物區別其他事物的特點,通過對比可以找出差異,有助于進一步加深對新知識的理解,揭示新知識的本質。
在數學教學中恰當地運用比較法,不但能突出教學的重點,簡化某些教學環節,而且有利學生理解和掌握概念,提高解題能力和發展思維能力。下面我就談談比較法在初中數學教學中的應用。
一、用比較法教學,加深對概念的理解
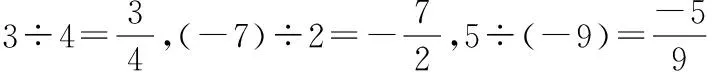
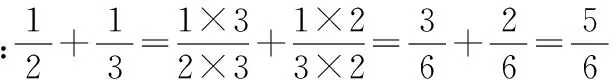
第三,分式的四則運算順序也可以類比分數進行,先做括號內的運算,然后再進行乘除運算,最后進行加減運算,這個順序和步驟正是分式四則混合運算的順序和步驟。概括地說是:“先乘除,后加減、括號內先進行”。
教學一元二次方程定義時,要求學生與一元一次方程定義比較。
有些比較,需要老師適當的引導,如在幾何教學中把相似三角形與全等三角形,它們的相同點是都具備對應角相等,對應邊成比例,但如果對應邊比例等于1,則相似即相等。又如有理式與分式比較,有理式包括整式和分式。分式是有理式的一部分,解方程與解不等式的解法大同小異。實踐證明,通過比較法能把一些易混淆的概念清楚地區分出來,使學生掌握和運用數學概念解決問題方面,起到事半功倍的效果。
二、用比較法教學,加深對新知識理解
教材中有較多的內容,在講授新知識的同時可以聯系舊知識并進行比較,這無論對學生掌握知識還是培養思維能力都是十分有效的。例如,教一元一次不等式解法時先復習一元一次方程的解法,然后說明一元一次不等式與一元一次方程在解法上基本相同,不同點是不等式兩邊同時乘以或除以同一個負數,不等號方向改變。又如,解含有字母系數的一元一次方程,分式方程都可以與解一元一次方程相比較,三角形相似判定定理與全等三角形判定定理比較,等等。初中數學的每個新知識點幾乎都可以找到一個與之聯系緊密的舊知識比較,采用比較法教學,不僅可以鞏固原有的知識,而且使新知識在比較中納入學生已掌握的知識結構中,把舊知識可能引起的負向遷移轉化為正向遷移。這樣,既順利完成新知識教學,又有利幫助學生建立科學的認知結構。
三、用比較法教學,提高解題能力
初中教學教材內容豐富,展現在學生面前的是千變萬化的數學題。學生在教師正確指導下,運用學過的知識,技巧和方法,通過認真比較,不但能掌握解題方法,而且能提高解題能力。例如,上因式分解復習課時,由于因式分解內容多、方法多,給出一個多項式學生往往不懂如何解答。這樣可以引導學生通過比較多項式的項選適當方法,如:(1)有兩項考慮用平方差方式;(2)有三項考慮用完全平方公式或(x+p)(x+q)的形式。通過比較復習,不僅使學生掌握因式分解的方法,還能使學生在較少時間內復習較多內容,提高復習效率和解題綜合能力。
此外,開立方與開平方,中心對稱與軸對稱;扇形面積公式與三角形面積公式等等,都可以通過類比和對比進行教學,這種數學方法的教學,學生在學習過程中能較輕松地接受新知識。在教學中運用比較法常常能把抽象問題變具體,把復雜問題變簡單,化難為易,使學生較易找出解題方法。在實踐中也證明,這種比較法的數學方法,學生掌握的知識扎實,理解也較好。當然,比較法只能用來幫助我們建立猜想,作為研究問題的線索。
總之,通過對比學習訓練,學生大腦中原來的思維定勢被打破,并很快升華到一個新的水平,在新的高度上重新形成一個新的思維定勢。靜態的思維方式被轉化動態的思維方式,有利于培養學生的動態發散性思維能力。學會學習新知識、新方法學習方法,形成從容跨入新的知識境界的能力,進而造就學生良好的數學素質和學習探討能力。

