軟巖隧洞的支護設計方法研究

邱 敏，鹿 寧

(中國電建集團西北勘測設計研究院有限公司,西安 710065)

?

軟巖隧洞的支護設計方法研究

邱 敏，鹿 寧

(中國電建集團西北勘測設計研究院有限公司,西安 710065)

由于軟巖的力學參數較低，開挖后變形明顯，塑性區深度較大，支護措施的設計具有很大難度，把握不好就會造成支護措施的浪費或者出現支護破壞問題，因此有必要對如何設計合適的支護措施做進一步的研究。通過巖體地質分類系統確定量化的支護時機，通過軟巖隧洞進行穩定計算得到支護方案。該方法只需通過平面有限元計算即可較快地得到支護時機和相應的支護措施。筆者在印尼某水電站引水隧洞中采用該方法進行了支護計算，說明了該方法在軟巖隧洞支護設計中簡便、可行。

軟巖；隧洞；支護

0 前 言

隨著越來越多地下工程的建設，各種復雜地質條件在地下工程中均可能出現。其中在軟巖中開挖的長距離隧洞工程，其支護措施和支護時機的確定一直是工程建設中存在的難題。20世紀60年代，拉布采維茨將新奧法應用于地質不良的奧地利的馬森貝格道路隧道中，由此開創了新奧法作為隧道設計方法的先河；經過多年的工程實踐，新奧法理論已被廣泛應用于地下工程的開挖支護設計中。新奧法理論即是盡量利用圍巖自承能力支撐洞室穩定，而這個“盡量”即是最大化地發揮圍巖自身的承載作用，確定最佳支護時機。所謂確定支護時機，就是將圍巖自承能力確定在一個恰當的數值，這就要求支護應在恰當的時候敷設，過早或過遲均不利。其支護剛度也不能太大或太小，必須是能與圍巖密貼的柔性薄層，允許有一定變形，以使圍巖釋放應力時起卸載作用，但不會有彎矩破壞的可能。

1 相關理論

1.1 應力釋放

巖體在開挖過程中，是開挖巖體部分的應力釋放過程。而開挖后應力釋放則是由于臨空面產生后，圍巖由3軸受壓狀態改變為雙軸受壓狀態，失去有效壓應力后逐漸變為松弛狀態的漸進過程。如果圍巖材料是彈性材料，其彈模的徑向變形可等效為一個拉應力逐漸增加的過程，直到拉應力等于初始地應力時，其徑向變形也靜止不變。因此，實際開挖過程是一個臨空面壓應力由初始地應力減小為零的過程，根據此理論，研究者提出采用逐步降低“反轉地應力”的方法模擬圍巖開挖后應力釋放過程。在有限元模型中，“反轉地應力”通過在開挖邊界上作用與原有支撐力相反的等效結點力來模擬，具體公式為：

(1)

式中：σj為第j-1次開挖引起地應力重分布后的應力場； [Bi]為開挖掉單元i的幾何矩陣；a為地應力釋放系數。

另外，如果圍巖材料為彈性材料，文獻[1]提出，應力釋放可以通過逐步降低開挖體的彈性模量來進行模擬，即彈性模量折減法。

1.2 隧洞開挖縱向變形曲線

隧洞開挖的過程是一個三維動態過程，隨著掌子面的推進，巖體應力、臨空面變形也隨之變化。國內外很多學者開展了隧洞開挖的分析研究[2-3]。其中三維效應歸納為2個方面：① “空間效應”，即掌子面約束作用所產生的影響。距掌子面越近，影響越大，距掌子面越遠，影響越小，到達某種距離后影響基本上可以消除。② “時間效應”，遠離掌子面影響距離，變形仍然隨時間而增大的這一現象。以上2種效應對一般巖體來說，前者占絕對影響，后者極難見到，一般僅存在高地壓的蠕變巖體中。

隧洞由于其軸向長度相對于其開挖跨度往往相差百倍，開挖支護計算往往采用平面應變模型進行分析；而平面模型僅模擬隧洞橫斷面，其掌子面推進的三維效應很難考慮。三維模型雖然可以考慮掌子面的三維效應，但往往因為三維模型計算量大，時間長，所要求的技術難度高而很難在工程中廣泛應用。所以國內外學者開始探索構造一條能夠反映徑向位移和掌子面進尺之間關系的函數曲線，以之運用于平面模型計算中，取代三維模型計算。2008年，Unlu and Gercek[4]通過大量實驗提出了能準確反映圍巖塑性，而且能考慮塑性區影響的隧道位移隨開挖面(撐子面)的變化曲線-LDP(LONGITUDINAL DEFORMATION PROFILE)曲線的公式如下：

(2)

(3)

(4)

(5)

式中：Rp為最大塑性區深度，m；u0為掌子面的徑向位移，m；Rt為隧洞半徑，m；X為開挖斷面到掌子面的距離(即無支護長度)，m；umax為最大徑向位移，m。

通過求解曲線，就將平面模型中的計算結果與掌子面推進距離建立了關系。

1.3 地質巖體分類

目前工程地質工作中對于圍巖分類方法眾多，其中常用的分類方法是國際《工程巖體分級標準》的BQ法、地質力學系統的RMR分類方法及巴頓等人提出的巖體質量分類Q系統法。BQ法多見于國內工程，國外工程中多采用RMR法和Q系統法[5]。蔡斌、喻勇、吳曉銘[5]在經過大量工程分類資料的基礎上，得到了BQ法與RMR法、Q系統法之間轉換的經驗公式[6]。工程巖體質量指標BBQ值與Q 系統法分類指標Q值呈指數關系，其關系為：

BBQ=69.44ln(Q)+161

(6)

工程巖體質量指標[BBQ]值與地質力學分類RRMR值呈線性關系，其關系式為：

BBQ=6.0943RRMR+80.786 (R=0.81)

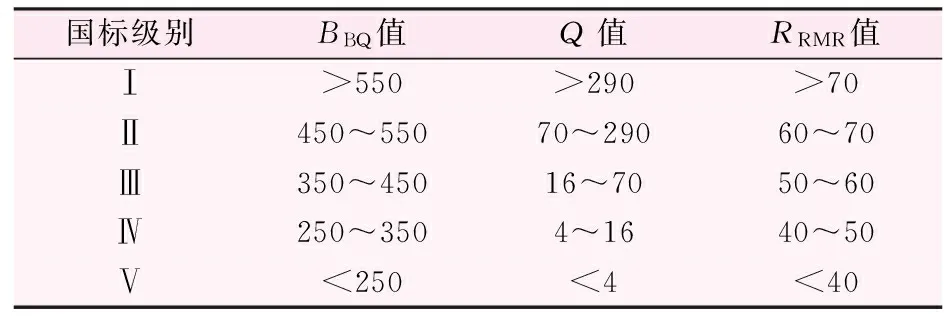
(7)

根據總結多年的工程實踐，巴頓1974年提出了掌子面到支護面的最大距離(即無支護長度)公式，如下：

(8)

式中：S為掌子面到支護面的最大距離；EESR為開挖支護比；Q為Q值。

由此，無論工程采用何種巖體分級方法，均可以通過公式(8)求出最大無支護長度，這就為支護時機的判斷給出了量化依據。

2 分析思路

通過第1.3節所述的巖體分類方法，換算出不同巖體分級下的無支護長度。而第1.2節LDP曲線的計算則可求出該長度對應的徑向圍巖變形，也即是開挖至掌子面時，未支護巖體與支護巖體相鄰處的徑向變形。按照從此處開始進行支護考慮(可根據實際情況取安全系數)，則可以通過此處的變形反推圍巖承擔的地應力或者應力釋放率，從而得出支護時機以及支護措施承受的荷載。

3 工程案例

本文依據上述思路，采用平面有限元對某水電站引水隧洞進行了圍巖支護計算。

某水電站位于印度尼西亞西爪哇島，為長引水式電站。引水隧洞全長約2 192 m，采用馬蹄形斷面開挖，最大開挖跨度為5.9 m。依據RMR分級，引水隧洞途經洞段圍巖為3類新鮮角礫巖和4類新鮮黏土巖，單軸抗壓強度分別為15 MPa和5 MPa，均為軟巖。引水隧洞所處最大平均埋深130 m。

本文以3、4類新鮮黏土巖洞段為例，對比及時支護和適時支護2種情況下，圍巖的位移、塑性區分布以及支護結構的受力情況。

3.1 地質巖體分類和力學參數

巖體分類及力學參數見表2。

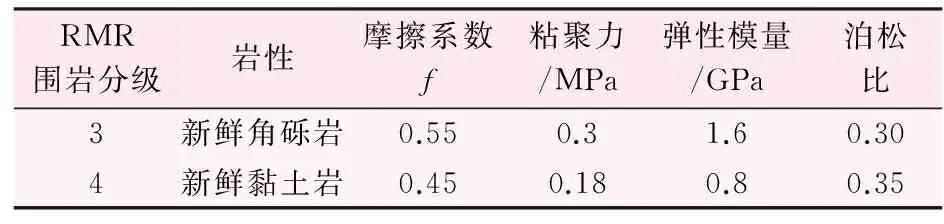
表2 巖體分類及力學參數表

3.2 地應力模擬

對于軟巖，可根據海姆假說[7]確定地應力場，假定巖體是理想的塑性體，地應力隨深度按自重增加。所以，圍巖初始地應力如表3所示。

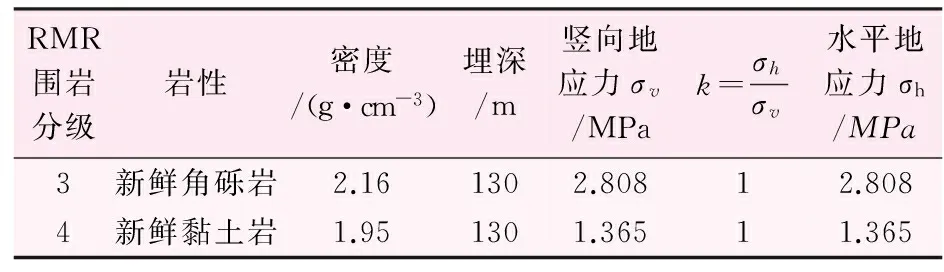
表3 初始地應力表

注：k為側壓系數。

3.3 支護時機確定

按照第1.3節和第1.2節所述進行計算，可得到各類巖石的無支護最大跨度、圍巖徑向變形和應力釋放率。具體見表4。

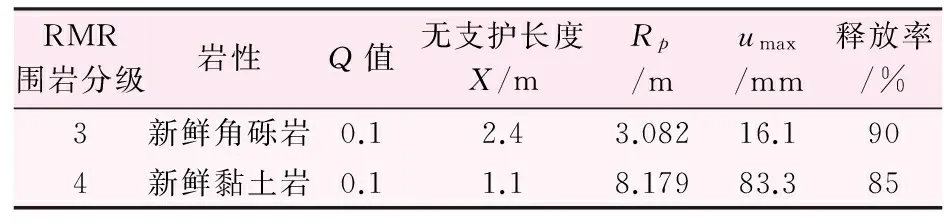
表4 巖體無支護最大跨度、圍巖徑向變形和應力釋放率表

3.4 計算結果對比

根據以上的計算，3類巖體的無支護長度是2.4 m,支護措施為15 cm厚的掛網噴射混凝土，錨桿長4.5 m，間排距1.5 m×1.5 m；4類巖體的無支護長度是1.1 m,支護措施為15 cm厚的掛網噴射混凝土，錨桿長4.5 m，間排距1.5 m×1.5 m，鋼支撐采用H203×89×19.3，間距1.5 m。

適時和及時支護2種情況下的圍巖位移、塑性區深度和支護結構應力對比見表5。

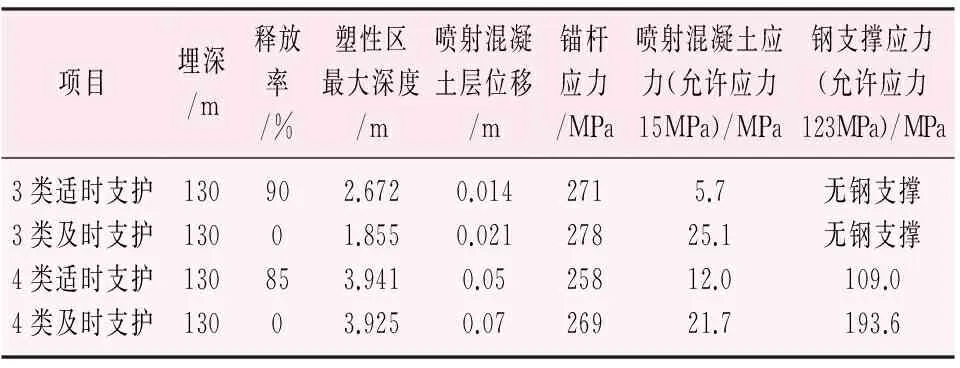
表5 計算結果表

通過計算，可見當及時支護與適時支護雖然支護時機不同，但在相同支護情況下，3類和4類圍巖的屈服深度隨支護時機的延后都有所增加，兩者規律基本一致，其中3類巖石的塑性區深度變化更大。由于及時支護情況下支護結構承擔了圍巖開挖后所有荷載，所以其支護結構受力明顯大于適時支護，變形大于適時支護，而且噴射混凝土的應力超過了允許應力15 MPa。而適時支護的支護結構滿足噴射混凝土允許應力，變形也小，采用適時支護滿足支護結構的安全要求。計算顯示，3類和4類圍巖噴混凝土的變形和支護應力規律與之一致，其中3類巖石的變化更大。由此可見，圍巖分級越高，彈模越大，圍巖荷載釋放的就越多，其適時支護所取得的效果就越好。

4 結 語

本文給出了確定支護時機的量化方法，并用于軟巖隧洞的開挖支護設計中,得到了一些有益的成果。

從中可見，采用適時支護解決了軟巖圍巖的支護設計問題，并證明了合理的選擇支護時機對于軟巖洞室支護結構設計的必要性；不合適的支護時機往往會增大支護結構的安全風險，而合理的支護時機的選擇不僅節約工程材料、降低工程造價，并且能夠保證支護結構的安全。

[1] 何欣,曹懷園,劉永智等.Phase2軟件在隧洞開挖圍巖支護時機中的應用[J].西北水電,2015(03)：49-53.

[2] 朱霜華.隧洞中軟質巖石收斂變形與量測分析[J].西北水電,2004(01)：6-8.

[3] 茍富民.烏龍山抽水蓄能電站地下廠房洞室圍巖穩定性分析研究[J].西北水電，2007(02)：13-18.

[4] Hoek, E., Carranza-Torres, C., Diederichs, M.S. and Corkum. integration of geotechnical and structural design in tunneling[C]//Proceedings University of Minnesota 56th Annual Geotechnical Engineering Conference.Minneapoils,29 February 2008.

[5] 蔡斌, 喻勇,吳曉銘.《工程巖體分級標準》與Q分類法、RMR分類法的關系及變形參數估算[J].巖石力學與工程學報, 2001,20(z1)：1677-1679.

[6] R. K. Goel,Bhawani Singh， Rock mass classification[M].ISBN: 978-0-08-043013-3, 1999.

[7] OTIS WILLIAMS， TUNNELS AND SHAFTS IN ROCK (EM 1110-2-2901)[S].Washington, DC 20314-1000, 1997.

Study on Design Methods for Support of Soft Rock Tunnel

QIU Min, LU Ning

(Northwest Engineering Corporation Limited, Xi'an 710065,China)

Due the mechanics parameters of soft rock are lower. The rock after excavation deforms obviously. The deformation depth in the plastic zone is greater. So, it is quite difficult to design the support measures. Otherwise waste or failure of the support measures is caused. Therefore, how to properly design the support measures shall be further studied necessarily. The quantitive support time is finalized by the geological classification system of rockmass. Through the stability calculation of the soft rock tunnel, the support proposal is produced. By application of this method, the support time and measures can be obtained quickly through the plane finite element calculation only. This method is practiced for support calculation of the headrace tunnel in Indonesia, demonstrating that the method is simple and feasible in the support design of the soft rock tunnel. Key words: soft rock; tunnel; support

1006—2610(2016)05—0032—03

2016-05-30

邱敏(1981- )，女，四川省成都市人,高級工程師，主要從事水工設計工作.

TV672.1；TV554.12

A

10.3969/j.issn.1006-2610.2016.05.008