變點方法在多項分布數據中的應用*
白艷麗,訾雪旻
(天津職業技術師范大學理學院,天津 300222)
?
變點方法在多項分布數據中的應用*
白艷麗,訾雪旻
(天津職業技術師范大學理學院,天津 300222)
利用變點方法,建立了基于多項分布數據這種復雜數據的監控模型,通過數值模擬,驗證了檢驗統計量的優良性,所做變點模型能夠準確地找到變點的位置及變點估計值,為更多的實際應用提供有力依據.
多項分布數據;變點方法;漸近正態;同質檢驗
1 問題描述
當對生產過程進行控制時,需要對產品數據進行收集分析,當統計過程可控時,數據的數值特征就會服從于統計學上某個穩定的分布,如正態分布,二項分布等,相反的,當統計過程失控時,數據分布必然會發生一定的變化,當檢測到此變化并報停生產,就可以達到控制產品質量的目的.在統計質量控制中,變點理論有著非常廣泛的應用,將變點方法用于不同的數據類型時,對不同的數據特征進行分析,當數據出現異常,其數據分布參數發生相應的變化,這樣就可以將變點位置以及變點值估計出來,從而控制質量.本文將變點方法應用于多項分布數據類型,研究得到適合它的變點監控模型.
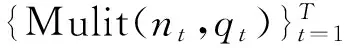
接下來,需要構造基于多項分布數據的變點模型,假設數據產生的概率發生變化,那么變點模型如下:
(1)
這里τ0>0,很顯然,它是兩個樣本出現差異的分界點,也就是要研究的一個未知的變點,其中qs=(qs1,…,qsp)T,s=0,1.想要檢驗是否真的存在變點,就相當于在做一個檢驗問題,將零假設與備擇假設記作:H0:τ0=T,H1:τ0 如上所述,變點檢驗問題與同質檢驗有相似之處,對于同質檢驗來說,更有效的方法是二分法和經典的卡方檢驗的方法,先構造關于兩個多項樣本Z1τ和Z2τ的同質檢驗的皮爾森卡方檢驗統計量,如下: (2) (3) 式(3)中Z1τ,j和Z2τ,j分別是Z1τ和Z2τ的j階成份,Lτ是從K2中移出來的分量式,這樣,所定義的Lτ就可以總是被很好用于研究.另外在檢驗過程中有可能出現很多的變點,那么為了達到檢驗目的,應該復查所有可能的變點,因此定義了新的檢驗統計量Sp, (4) 這里0 對于所構造的統計量Sp的漸近行為,做以下的假設: (A1)當p→∞ 時,max1≤j≤pqoj→0; (A2)當p,N→∞,0 根據假設的成立可以得到以下的結論: (i)假設H0和(A1),(A2)成立時,當p,N→∞時,Sp的期望和方差如下: 這里ΔT=[b(T-1)]-[a(T-1)]+1. (ii)假設(A3)成立,當p,N→∞時 證明如下. 證明(i) 可以將Lτ寫成(5)式的形式: (5) 這樣,在零假設下將Lτ改寫下式(6)的形式: (6) 因此,就可以得到 (7) (8) 在假設(A2)下: 在假設(A1)下,var[Sp,2]/var[Sp,1]→0,最終得到 (9) 證明(ii) (10) 并且存在γ∈(0,∞),使得 (11) 因此可以得到,當p,N→∞時, (12) 我們先來證明(12)式,記El-1(·)=E[·|FN,l-1],有: 因此可以看到: 也就是說γ=1/4, (13) (14) 通常,可以寫成如下(15)式形式: (15) 式中: 由假設(A1)和(A2)和一范數的概念可知: 在假設(A3)下,可以得到: 同理B3=o(1).至此(11)式證明完畢. (16) 應用證明(12)式相似的方法在(10)式的證明中,可以得到: 表1 p=1 000,N=1 000,T=100時,數值 根據以上產生的數據,利用統計軟件R畫出其密度函數圖像,如圖1所示. X 下面建立常規的控制圖,將數據中的變點一一找到,控制圖如圖2所示: X 從圖2可以看出所得到的100個數據中有12個超出了控制線,分別是第33,37,38,55,59,70,76,78,80,85,98,100個.并且返回到變點的估計值分為9 574.480,9 560.900,9 571.593,9 617.917,9 576.615,8 625.516,8 744.992,8 754.763,8 670.260,8 718.625,9 544.144,9 712.753. 本文針對于一種實際生產出現最多但研究卻很少的多項分布數據,將變點模型與數據特征值很好的結合起來,構造優良統計量并用統計軟件編寫相應的統計程序通過數據模擬,驗證了該方法的正確性與穩健性. [1]王毓芳,肖詩唐.統計過程控制的策劃與實施[M].北京:中國經濟出版社,2006:70-71. [2]徐會作.質量控制圖經濟設計研究[D]. 上海:華東師范大學,2008. [3]吳喜之.復雜數據統計方法-基于R的應用[M].北京:中國人民大學出版社,2012:176-183. [4]肖枝洪,朱強.統計模擬及其R實現[M].武漢:武漢大學出版社,2010:83-88. [5]Shewhart,W.A..The application of statistics as an aid in maintaining Quality of a manufactured production[J].JASA,1925,20:546-548. [6]Robert,S.W..Control Chart Test Based on Geometric Moving Averages[J]. Technometrics,1959,1(3):239-250. [9]譚長春.變點問題的統計推斷及其在金融中的應用[D].合肥:中國科學技術大學,2007. [10]朱嬰子.統計過程控制在流程化工生產中的應用[D].南京:南京理工大學,2003. [11]Hunter,J.S..The exponentially weighted moving average[J].Joumal of Quality Technology,1986,18:239-250. Application of Change Point Method in the Multinomial Distribution Data BAI Yan-li, ZI Xue-min (School of Science, Tianjin University of Technology and Education,Tianjin 300222, China) This paper uses the change point method to establish the monitoring model of the complex data based on the multinomial distribution data. Through the numerical simulation, it is proved that the test statistic is excellent. The change point model can accurately find the position of the change point and the estimate of the change point, which can provide a strong basis for more practical application. multinomial distribution data; change point method; asymptotic normality; homogeneity test 1673-2103(2016)05-0011-07 2016-04-20 國家自然科學基金面上項目(11271205) 白艷麗(1990-),女,山西晉中人,碩士研究生,研究方向:統計過程控制. 訾雪旻(1977-),女,安徽亳州人,教授,博士,研究方向:統計過程控制. O213.1 A
2 構造檢驗統計量
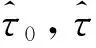
3 統計量的漸近行為
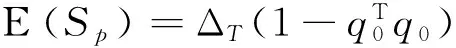
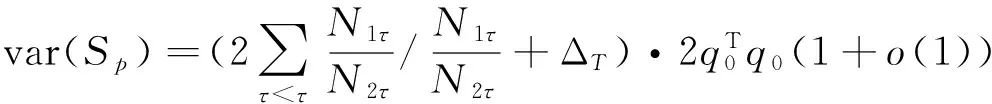

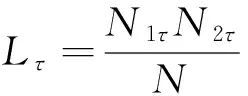


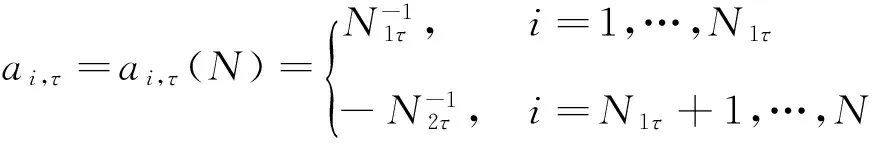
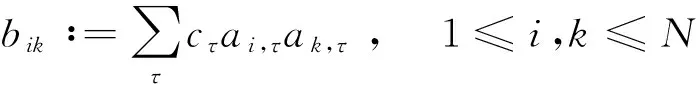

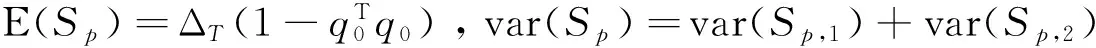
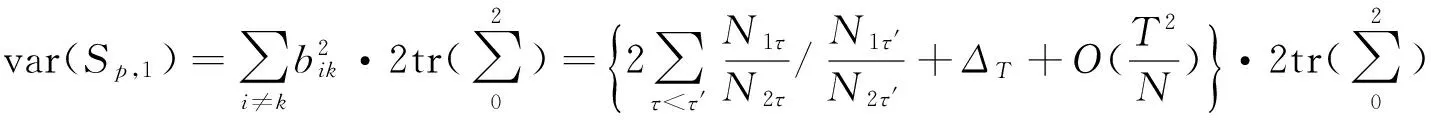




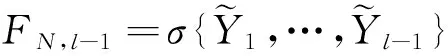

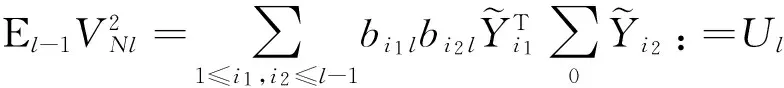
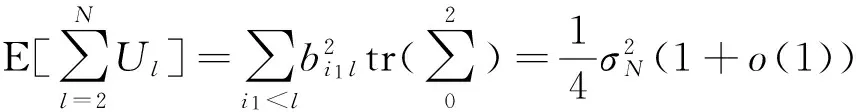
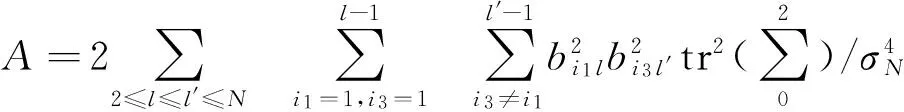
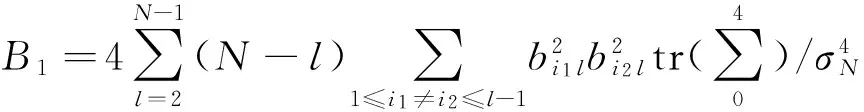
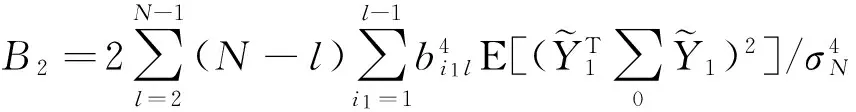

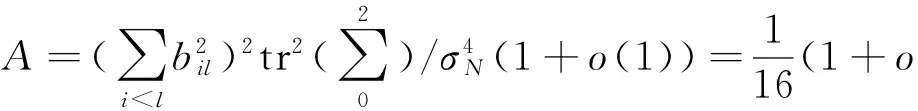
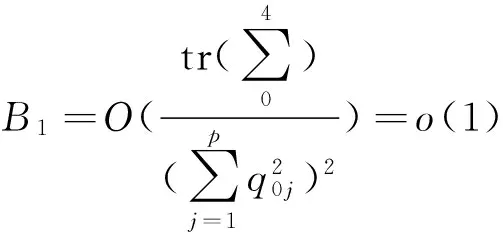

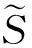
4 數據模擬


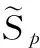


5 結束語

